MATLAB | 数学模型 | 传染病 SIR 模型的参数确定

传染病模型大家都很熟悉，那么假设已经有了统计的 S,I,R 的数据，怎么进行参数确定呢，在讲这一块之前首先先简要描述一下传染病 SIR 模型：

传染病模型简述

$S$ 代表易感者(susceptibles)，$I$ 代表患者(infectives)，$R$ 代表康复且不会再得的人群(recovered individuals)。易感者和患者接触后有概率变成患者，患者有概率康复变成康复者：

$$S⟶I⟶R$$

感染者增加速度和感染者人数和易感者人数都有关系，而感染者痊愈的人数变化速度只和感染者人数有关，

$$\begin{array}{rl}\frac{dS}{dt}& =-\beta IS\\ \frac{dI}{dt}& =\beta IS-\gamma I,\\ \frac{dR}{dt}& =\gamma I,\end{array}$$

为了将离散的问题连续化，同时为了减少待确定参数，我们将模型无量纲化（就是把单位从人数变成百分比），这里不考虑死亡（考虑死亡的模型我放在练习题里啦~），假设总人数为$N=S+I+R$:

$$\begin{array}{rl}\frac{dN}{dt}& =\frac{dS}{dt}+\frac{dI}{dt}+\frac{dR}{dt}\\ & =-\beta IS+\beta IS-\gamma I+\gamma I=0\end{array}$$

因此总人数保持不变，可以做如下无量纲化：

$$S=N\bar{S},I=N\bar{I},R=N\bar{R},t=\bar{t}/\gamma$$
$$\bar{S}+\bar{I}+\bar{R}=1$$

带入之前的微分方程组得：
$$\begin{array}{rl}\frac{d\bar{S}}{d\bar{t}}& =-R_0\bar{I}\bar{S}\\ \frac{d\bar{I}}{d\bar{t}}& =R_0\bar{I}\bar{S}-\bar{I}\\ \frac{d\bar{R}}{d\bar{t}}& =\bar{I}\end{array}$$

其中$R_0=\beta N/\gamma$，所以我们就只有一个参数需要确定。

实验数据

为了做实验我们随机生成了一组数据：这里的 $R_0$ 为了和康复者 $R$ 的初始占比做区分，写作了 r0：这里我们将 $R_0$ 数值设置为5，并添加了噪声干扰，生成了如下实验数据：

%% 数据生成
S0 = 99/100;                % 初始易感者占比
I0 = 1/100;                 % 初始感染者占比
R0 = 0;                     % 初始康复者占比
y0 = [S0, I0, R0]; 
r0 = 5;% S = y(1), I = y(2)
sir_model = @(t, y, r0) [- r0*y(1)*y(2);          % dS/dtr0*y(1)*y(2) - y(2);   % dI/dty(2);                  % dR/dt
];exp_t = linspace(0, 10, 101).';
[sim_t, sim_y] = ode45(@(t, y) ...sir_model(t, y, r0), exp_t, y0);
sim_y = sim_y + (rand(size(sim_y)) - .5).*.05;  % 添加噪声干扰
sim_y(sim_y < 0) = 0;
sim_y = sim_y./sum(sim_y, 2);exp_S = sim_y(:,1);
exp_I = sim_y(:,2);
exp_R = sim_y(:,3);
save experimental_data_SIR_nondim exp_S exp_I exp_R exp_t

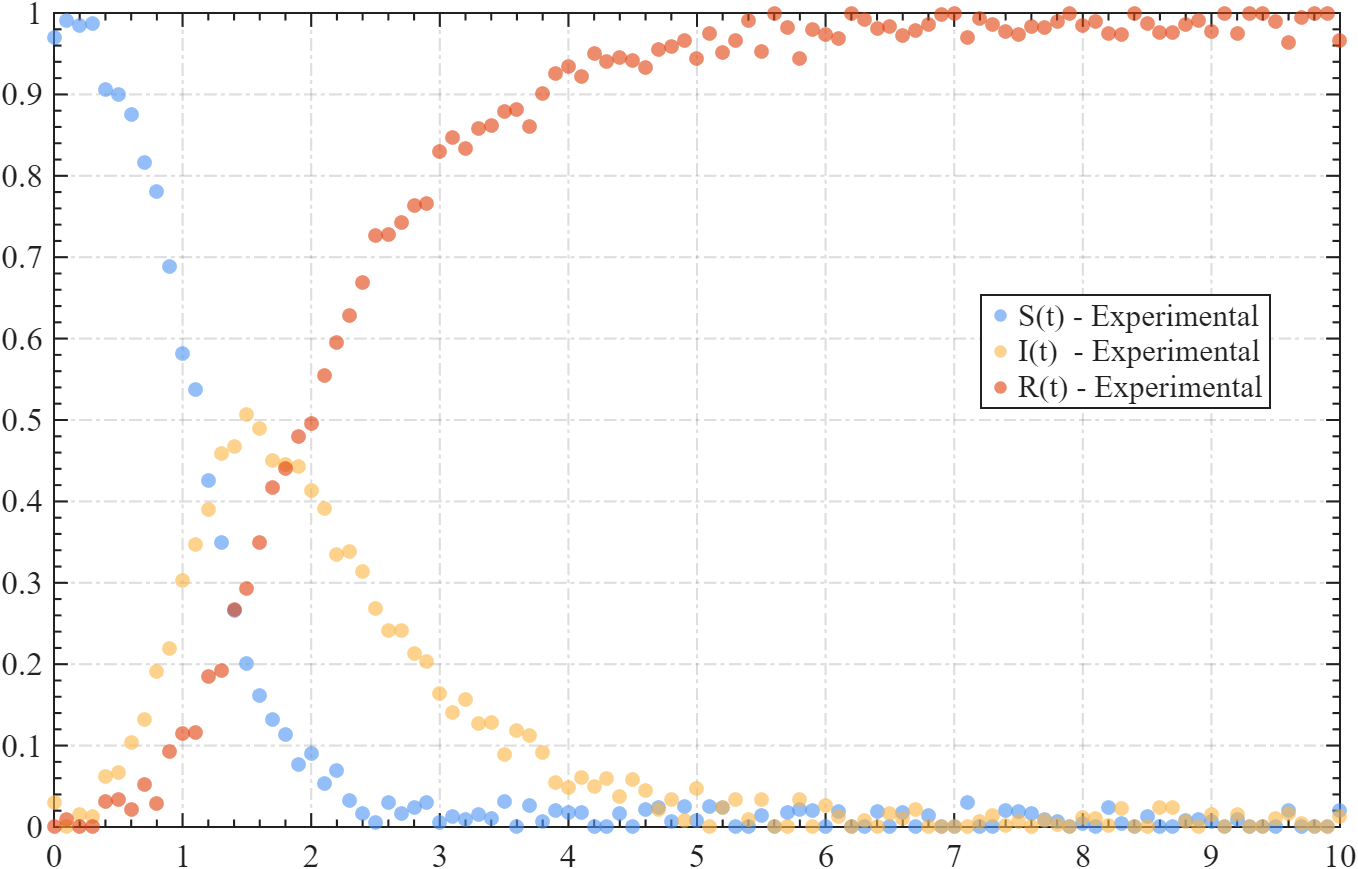
该数据可以通过如下方式导入：

% 数据导入
SIRVD_data = load('experimental_data_SIR_nondim.mat');
exp_t = SIRVD_data.exp_t;
exp_S = SIRVD_data.exp_S;
exp_I = SIRVD_data.exp_I;
exp_R = SIRVD_data.exp_R;
disp('Experimental data loaded successfully from .mat files.');

最小二乘估计

思路非常简单，我们通过设定 $R_0$ 和初始数据，使用龙格库塔法进行模拟，然后尝试找到使得模拟数据和真实数据差距最小的 $R_0$，即：

$$\begin{array}{rl}{R}_0=\text{argmin}\sum _i& (S_{\text{true}}(t_i)-S_{\text{model}}(t_i){)}^2+(I_{\text{true}}(t_i)-I_{\text{model}}(t_i){)}^2\\ & +(R_{\text{true}}(t_i)-R_{\text{model}}(t_i){)}^2\end{array}$$

这个目标函数有很多种编写方法，这里提供两种：

目标函数一

其中 simulate_SIR 函数使用设定的 $R_0$ 进行数据模拟， objective 将模拟数据和真实数据作比较，还是比较清晰的：

% 目标函数编写方法一
function outputs = simulate_SIR(t_data, y0, r0, tspan, var_type)[t_sim, y_sim] = ode45(@(t, y) [- r0*y(1)*y(2);          % dS/dtr0*y(1)*y(2) - y(2);   % dI/dty(2);                  % dR/dt], tspan, y0);y_interp = interp1(t_sim, y_sim, t_data, 'linear', 'extrap');switch var_typecase "S", outputs = y_interp(:, 1);case "I", outputs = y_interp(:, 2);case "R", outputs = y_interp(:, 3);end
end
objective = @(params, t_data, S_data, I_data, R_data, y0, tspan) ...sum((S_data - simulate_SIR(t_data, y0, params, tspan, "S")).^2) + ...sum((I_data - simulate_SIR(t_data, y0, params, tspan, "I")).^2) + ...sum((R_data - simulate_SIR(t_data, y0, params, tspan, "R")).^2);

这个写法非常清晰，但是会调用很多次 simulate_SIR 函数。此外如果MATLAB 是老版本，请将 simulate_SIR 函数写在 m 文件的最后。

目标函数二

这个方法比较高效，就是把SIR三组数据拼在一起做最小二乘：

% 目标函数编写方法二
function y_interp = simulate_SIR(t_data, y0, r0, tspan)[t_sim, y_sim] = ode45(@(t, y) [- r0*y(1)*y(2);          % dS/dtr0*y(1)*y(2) - y(2);   % dI/dty(2);                  % dR/dt], tspan, y0);y_interp = interp1(t_sim, y_sim, t_data, 'linear', 'extrap');
end
objective = @(params, t_data, S_data, I_data, R_data, y0, tspan) ...sum(sum(([S_data, I_data, R_data] - simulate_SIR(t_data, y0, params, tspan)).^2));

参数确定

直接使用 MATLAB 自带的 fminsearch 函数即可：

% 使用 fminsearch 函数找到使得实验值和真实值差距最小的的 R_0
S0 = 99/100;                % 初始易感者占比
I0 = 1/100;                 % 初始感染者占比
R0 = 0;                     % 初始康复者占比
y0 = [S0, I0, R0]; 
r0_guess = 1;               % 猜测的 R0 (随便设置的初始值)
tspan = linspace(min(exp_t), max(exp_t), length(exp_t));
params_fit = fminsearch(@(params) objective(params, exp_t, exp_S, exp_I, exp_R, y0, tspan), r0_guess);
disp(['Estimated R0: ', num2str(params_fit(1))]);

计算出来 $R_0=4.9996$，还是比较准确的。

绘图

画个图展示一下拟合效果：

figure('Units','normalized', 'Position',[0,.4,.5,.5]);
axes('Parent',gcf, 'NextPlot','add');
% Palette
CList = [75,146,241; 252,180,65; 224,64,10; 5,100,146; 170,170,170]./255;
% 绘制真实数据
scatter(exp_t, exp_S, 50, CList(1,:), 'filled', ...'MarkerFaceAlpha',.6, 'DisplayName', 'S(t) - Experimental');
scatter(exp_t, exp_I, 50, CList(2,:), 'filled', ...'MarkerFaceAlpha',.6, 'DisplayName', 'I(t)  - Experimental');
scatter(exp_t, exp_R, 50, CList(3,:), 'filled', ...'MarkerFaceAlpha',.6, 'DisplayName', 'R(t) - Experimental');
% 绘制拟合数据
plot(sim_t, sim_y(:, 1), 'Color',CList(1,:), ...'LineWidth', 3, 'DisplayName', 'S(t) - Model');
plot(sim_t, sim_y(:, 2), 'Color',CList(2,:), ...'LineWidth', 3, 'DisplayName', 'I(t)  - Model');
plot(sim_t, sim_y(:, 3), 'Color',CList(3,:), ...'LineWidth', 3, 'DisplayName', 'R(t) - Model');
% 图像修饰
set(gca, 'Box', 'on', 'LineWidth',1, 'FontName','Times New Roman', ...'FontSize',16, 'XMinorTick','on', 'YMinorTick','on', ...'XGrid','on', 'YGrid','on', 'GridLineStyle','-.')
xlabel('Time', 'FontSize', 16);
ylabel('Fraction of Population', 'FontSize', 16);
title('SIR Model Fit ($R_0$)',...'FontSize', 20, 'Interpreter','latex');
legend('FontSize', 15, 'Location', 'best');

可以看到效果还是不错的：

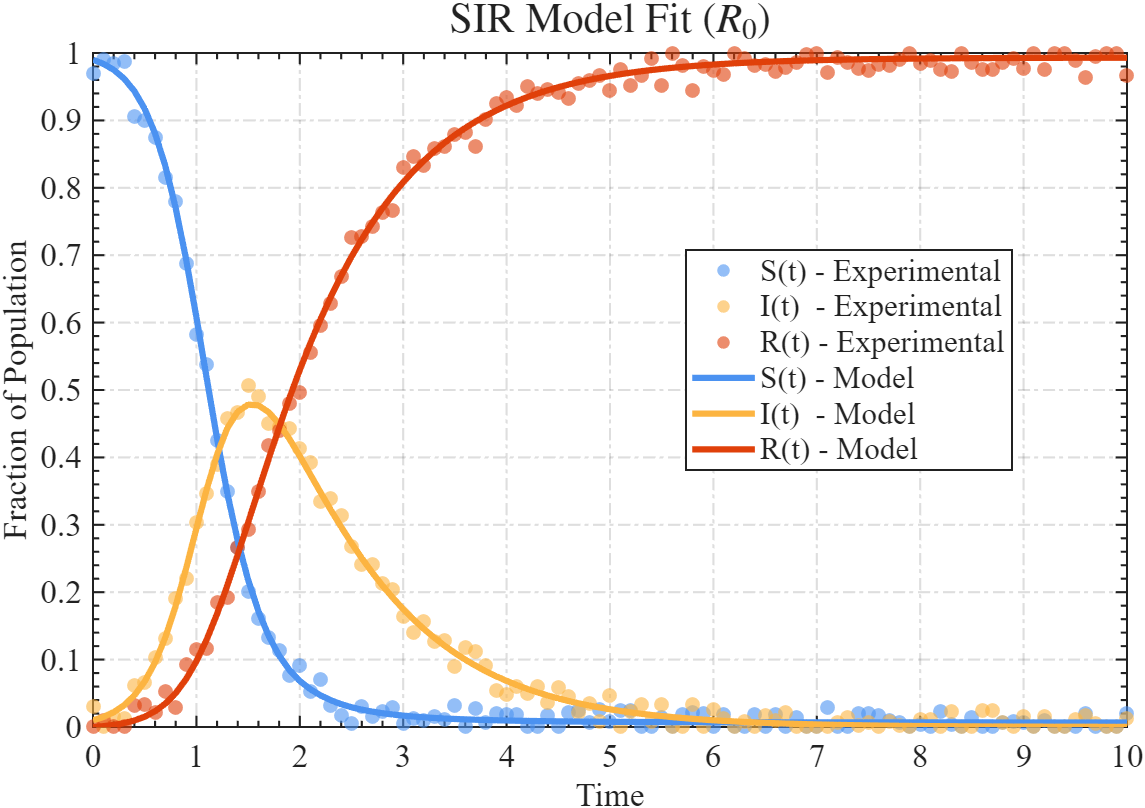
可以再生成点其他数据，比如 $R_0$ 为2的时候，拟合效果：

---

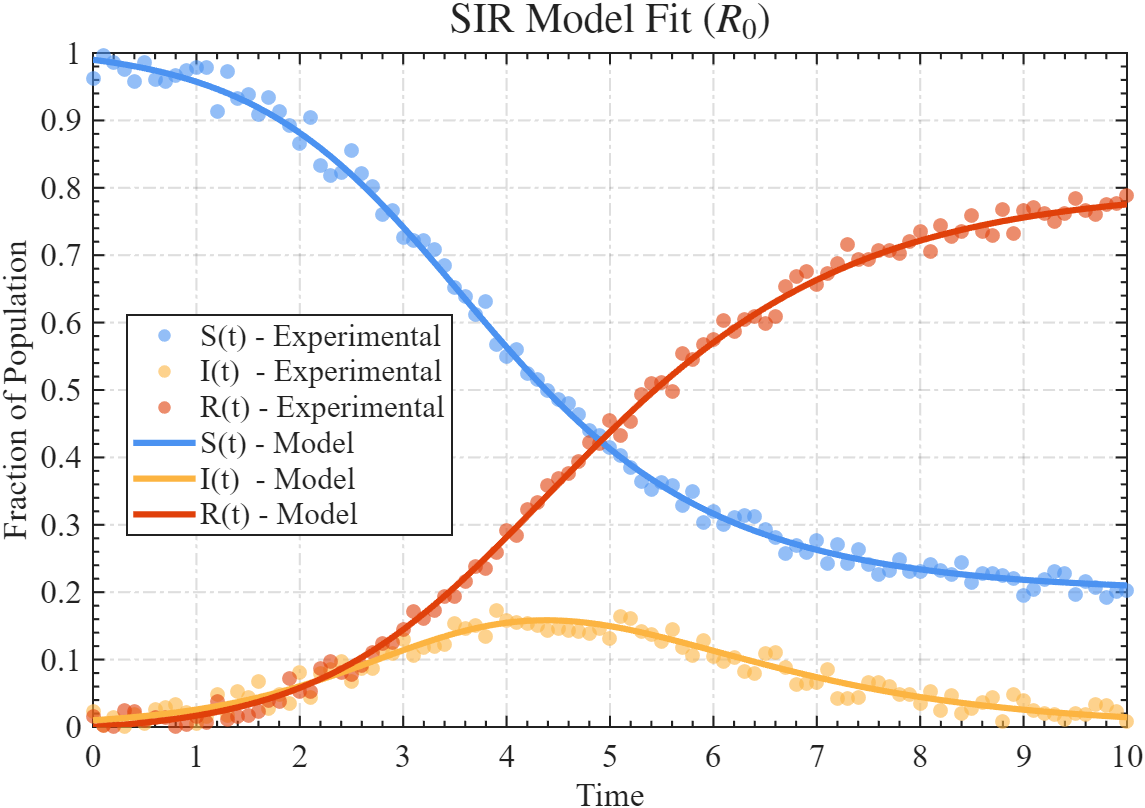
近似贝叶斯计算(Approximate Bayesian Computation)

名字比较好玩，简称 ABC 方法，该方法的本质是如下公式：

$$P(R_0\mid D)\propto P(D\mid R_0)P(R_0)$$

其中 $D$ 代表我们的真实数据，我们如果将 $P(R_0)$ 设置为均匀分布，就可以用 $P(D\mid R_0)$ 估计在真实数据下的参数可能的分布 $P(R_0\mid D)$。

使用这个方法的思路也很简单，就是我们在一定范围内随机生成一堆 $R_0$ ，获取模拟数据，试试每组模拟数据和真实值的差异，如果差异在可接受范围我们就先存一下这个 $R_0$ ，当存下一定量的 $R_0$ 后（比如1000个），把所有存下来的数取个均值：

% 数据导入
SIRVD_data = load('experimental_data_SIR_nondim.mat');
exp_t = SIRVD_data.exp_t;
exp_S = SIRVD_data.exp_S;
exp_I = SIRVD_data.exp_I;
exp_R = SIRVD_data.exp_R;
disp('Experimental data loaded successfully from .mat files.');S0 = 99/100;                % 初始易感者占比
I0 = 1/100;                 % 初始感染者占比
R0 = 0;                     % 初始康复者占比
y0 = [S0, I0, R0]; 
tspan = linspace(min(exp_t), max(exp_t), length(exp_t));
% S = y(1), I = y(2)
sir_model = @(t, y, r0) [- r0*y(1)*y(2);          % dS/dtr0*y(1)*y(2) - y(2);   % dI/dty(2);                  % dR/dt
];% ABC 方法
N = 1000;                      % 存储的符合条件的 R_0 个数
accepted_samples = zeros(N,1); % 存储的符合条件的 R_0 的数组
threshold = 0.001;             % 容许误差
r0_prior = [2, 8];             % 估计的 R_0 的范围fprintf('\r')
disp(['ABC sampling for threshold = ', num2str(threshold)])
disp('  0% ------------------------------ 100%')
fprintf('PROG ')
len_samples = 0;
while len_samples < N% 生成随机 R_0r0_sample = rand() * diff(r0_prior) + r0_prior(1);% SIR 模型的龙格库塔法模拟[~, y_sim] = ode45(@(t, y) ...sir_model(t, y, r0_sample), tspan, y0);y_sim_S = interp1(tspan, y_sim(:, 1), exp_t, 'linear', 'extrap');y_sim_I = interp1(tspan, y_sim(:, 2), exp_t, 'linear', 'extrap');y_sim_R = interp1(tspan, y_sim(:, 3), exp_t, 'linear', 'extrap');% 计算拟合数据和真实数据差异的均值distance = mean((exp_S - y_sim_S(:)).^2 + ...(exp_I - y_sim_I(:)).^2 + ...(exp_R - y_sim_R(:)).^2);% 如果均值小于阈值，则接受if distance < thresholdlen_samples = len_samples + 1;if floor(30*len_samples/N) > floor(30*(len_samples - 1)/N)fprintf('#')endaccepted_samples(len_samples) = r0_sample;end
end; fprintf(' END\r\n')mean_r0 = mean(accepted_samples(:, 1), 1);  % 可接受 R0 的均值
std_r0 = std(accepted_samples(:, 1), 0, 1); % 可接受 R0 的标准差
disp(['Mean R0: ', num2str(mean_r0(1)), ', Std R0: ', num2str(std_r0(1))]);

这里容许误差越小求出来的越精准，但是用时也会越长，例如设置为0.001时求解结果为：

• Mean R0: 5.0136, Std R0: 0.13391

例如设置为0.0005时求解结果为：

• Mean R0: 5.0002, Std R0: 0.016529

画个图：

% 绘图
figure('Units','normalized', 'Position',[0,.1,.5,.25]); axes('Parent',gcf, 'NextPlot','add');
histogram(accepted_samples(:, 1), 20, 'Normalization', 'pdf', 'FaceAlpha',.4, 'LineWidth',1);
set(gca, 'LineWidth',1, 'FontSize',16, 'Box','on', 'FontName','Times New Roman', ...'XMinorTick','on', 'YMinorTick','on', 'XGrid','on', 'YGrid','on', 'GridLineStyle','-.')
xlabel('$R_0$', 'FontSize', 16, 'Interpreter','latex');
ylabel('Density', 'FontSize', 16);
title('Posterior Distribution of $R_0$', 'FontSize', 20, 'Interpreter','latex');
xline(mean_r0(1), 'r', 'LineWidth', 2, 'DisplayName', 'Mean $R_0$', 'Interpreter','latex');

---

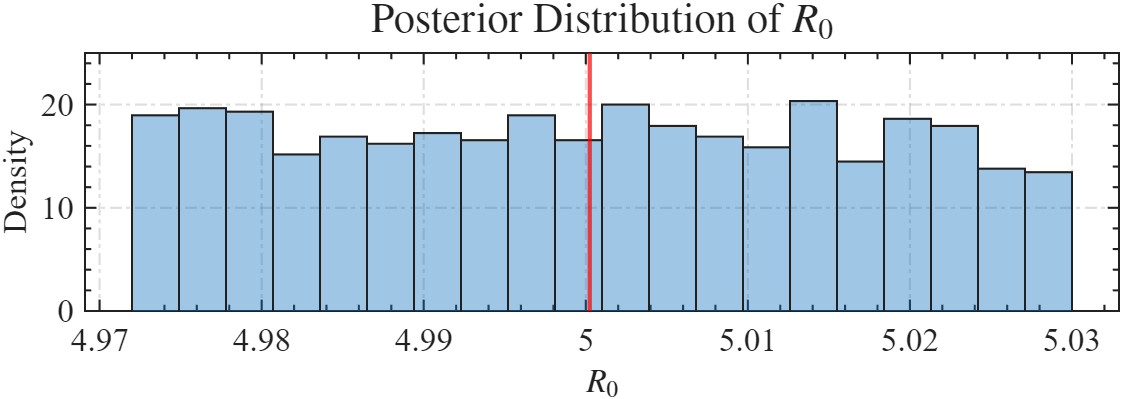
小测

既然你已经会了 SIR 模型参数估计，那么有三个参数需要确定的 SIRVD 模型一定难不倒你：

$$\begin{array}{rl}& \frac{dS}{dt}=-\beta SI-\nu S\\ & \frac{dI}{dt}=\beta SI-\gamma I-\mu I\\ & \frac{dR}{dt}=\gamma I\\ & \frac{dV}{dt}=\nu S\\ & \frac{dD}{dt}=\mu I\end{array}⟹\begin{array}{rl}& \frac{d\bar{S}}{d\bar{t}}=-R_0\bar{S}\bar{I}-\bar{\nu }\bar{S}\\ & \frac{d\bar{I}}{d\bar{t}}=R_0\bar{S}\bar{I}-\bar{I}-\bar{\mu }\bar{I}\\ & \frac{d\bar{R}}{d\bar{t}}=\bar{I}\\ & \frac{d\bar{V}}{d\bar{t}}=\bar{\nu }\bar{S}\\ & \frac{d\bar{D}}{d\bar{t}}=\bar{\mu }\bar{I}\end{array}$$
其中：

$$R_0=\frac{\beta N}{\gamma },\bar{\nu }=\frac{\nu }{\gamma },\bar{\mu }=\frac{\mu }{\gamma }$$

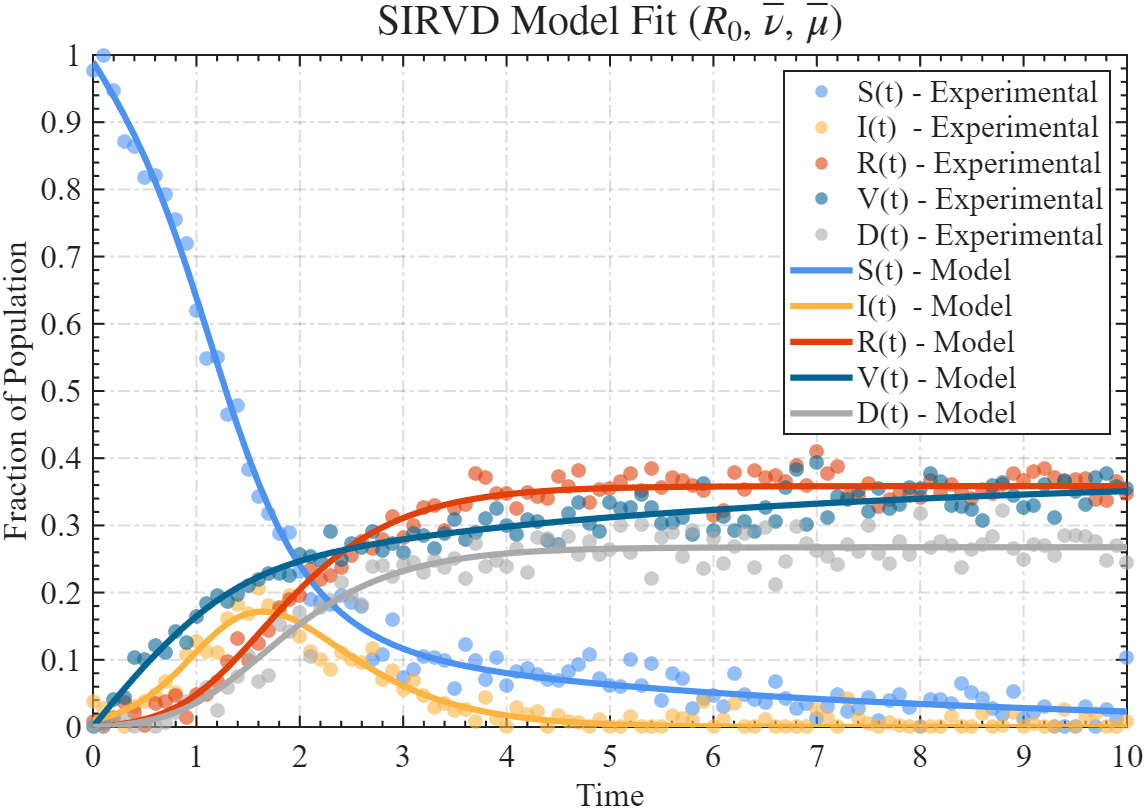
一起来试试叭，我在网盘里放了小测验的题目和答案~

• https://pan.baidu.com/s/193lmNOnoRzOLLupaeDJ0uQ?pwd=slan