Scikit-learn Python机器学习 - 回归分析算法 - 线性回归 (LinearRegression SGDRegressor)
锋哥原创的Scikit-learn Python机器学习视频教程:
https://www.bilibili.com/video/BV11reUzEEPH
课程介绍

本课程主要讲解基于Scikit-learn的Python机器学习知识,包括机器学习概述,特征工程(数据集,特征抽取,特征预处理,特征降维等),分类算法(K-临近算法,朴素贝叶斯算法,决策树等),回归与聚类算法(线性回归,欠拟合,逻辑回归与二分类,K-means算法)等。
Scikit-learn Python机器学习 - 回归分析算法 - 线性回归 (LinearRegression & SGDRegressor)
线性回归(Linear Regression)是一种基础的回归分析方法,它通过构建输入特征和输出结果之间的线性关系,来预测输出值。其核心思想是通过找到最合适的“拟合线”来预测未知数据的结果。
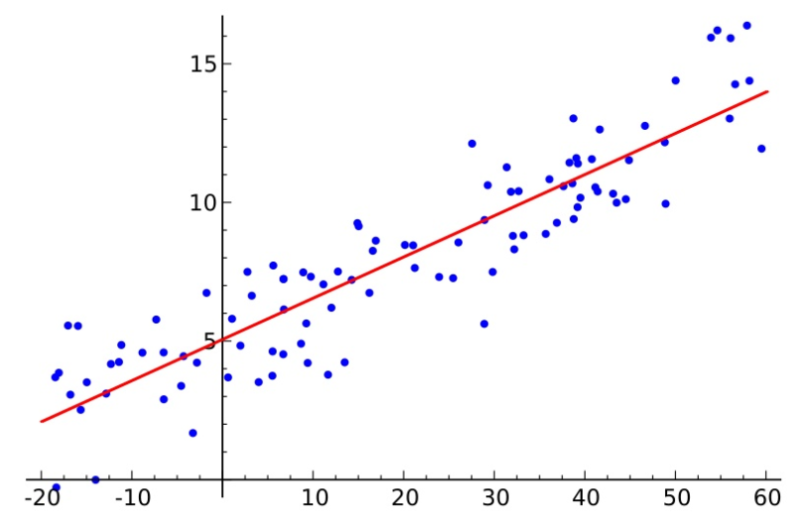
1,线性回归模型的基本原理

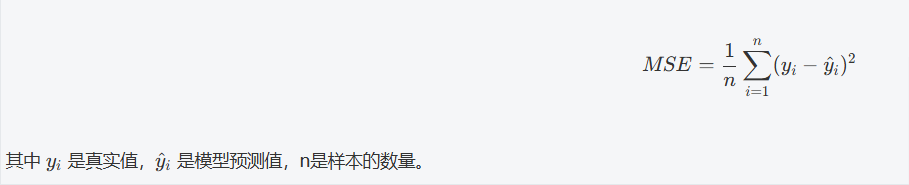
2,损失函数
在回归问题中,我们常用 均方误差(MSE) 作为损失函数,目标是最小化这个损失函数。均方误差计算公式为:
3,模型的求解
线性回归的目标就是通过最小化损失函数来找到最合适的 β 参数。我们可以通过 梯度下降法 或者 正规方程法 来求解。

4,梯度下降法
梯度下降法(Gradient Descent)是机器学习和深度学习中常用的一种优化算法。它的核心思想非常直观:我们通过不断“走下坡路”来找到一个最低点(即最优解)。
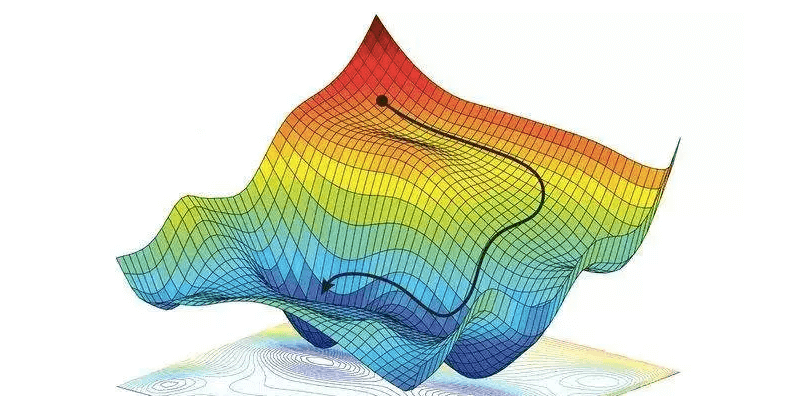
想象一下:
假设你站在一个山坡上,你的目标是找到山谷的最低点。你无法看到整个山谷的情况,只能看到你当前所在位置的周围环境。为了找到最低点,你需要根据当前的位置判断哪个方向最陡峭,然后朝着这个方向走一小步。每走一步,你就能让自己离最低点更近一些。
具体来说,梯度下降法是这样的:
-
山坡的斜率:在数学中,我们可以通过梯度来表示当前点的“坡度”或“斜率”。如果你在山坡的某个点站着,梯度就告诉你最陡的下坡方向。换句话说,梯度是一个向量,它指向函数下降最快的方向。
-
向梯度的反方向走:为了找到最低点,我们不是沿着梯度的方向走,而是沿着梯度的反方向走。因为梯度告诉我们的是上坡的方向,我们反着走就是下坡。
-
步长(学习率):每走一步时,我们需要决定步伐的大小,这就是所谓的学习率。如果步伐太大,可能会错过最低点;如果步伐太小,找到最低点的过程就会非常缓慢。
过程:
-
初始化:首先从一个随机点(位置)开始。这个点可以是任何地方,就像你站在山坡的某个随机位置。
-
计算梯度:在当前位置,计算当前点的梯度(坡度)。梯度告诉你最陡的上坡方向。
-
更新位置:沿着梯度的反方向走,更新你的位置。更新的幅度是梯度的反方向乘以步长(学习率)。
-
重复:不断重复上述步骤,直到你到达一个相对平坦的区域,或者你已经足够接近最低点。
数学公式
梯度下降的更新规则通常表示为:

例子:线性回归的梯度下降
假设我们要通过梯度下降法求解线性回归模型的参数(例如直线的斜率和截距)。我们可以使用梯度下降来最小化均方误差(MSE)损失函数。每次通过计算梯度,调整参数,最终找到一个合适的拟合直线。
关键要点:
-
步长(学习率):如果学习率设置得太大,可能会“跳过”最低点;如果设置得太小,算法收敛得非常慢。
-
局部最小值和全局最小值:梯度下降法有可能会停在局部最低点,但理想情况下我们希望找到全局最低点。为此,我们可以使用一些技巧,如随机初始化或动量法,来避免陷入局部最小值。
类比理解:
-
攀登山峰:梯度下降就像你在山中探险,通过触摸周围的环境(计算梯度)来确定下一步走向。
-
在迷雾中找路:如果你不能看到全貌,你就只能一步一步、逐渐判断方向,直到找到目的地。
5,API介绍
线性回归-正规方程使用 LinearRegression
LinearRegression 类的参数不多,但它们控制着模型如何拟合数据和如何计算。
sklearn.linear_model.LinearRegression(*, fit_intercept=True, copy_X=True, n_jobs=None, positive=False
)参数详解:
1. fit_intercept : bool, default=True
-
功能:决定是否计算模型的截距(也叫偏置项,即 $w_0$)。
-
详解:
-
fit_intercept=True(默认):模型会计算截距项 $w_0$。公式为 $\hat{y} = w_0 + w_1x_1 + w_2x_2 + ... + w_nx_n$。这是最常见的情况,除非你确信你的数据已经经过处理,其回归线理所当然地应该通过原点 (0,0)。 -
fit_intercept=False:模型会强制截距为 0。公式变为 $\hat{y} = w_1x_1 + w_2x_2 + ... + w_nx_n$。这通常只在你有很强的先验知识(即当所有特征都为 0 时,目标值必须为 0)时使用。
-
-
如何选择:
-
几乎总是保持默认值 True。
-
只有在非常特殊的情况下才设置为
False(例如,物理定律要求没有偏移)。
-
2. copy_X : bool, default=True
-
功能:决定是否复制特征数据
X。 -
详解:
-
copy_X=True(默认):在拟合模型之前,会创建特征矩阵X的一个副本。原始数据X不会被修改。这是安全的选择。 -
copy_X=False:模型会直接在原始数据X上进行计算。这可以节省内存,尤其是当X非常大时。但缺点是会覆盖原始数据。
-
-
如何选择:
-
通常保持默认值
True,以确保原始数据安全。 -
只有在内存极度紧张且你确定不再需要原始
X数据时,才设置为False。
-
3. n_jobs : int, default=None
-
功能:设置用于计算的 CPU 核心数量,用于并行化计算。
-
详解:
-
n_jobs=None(默认):使用 1 个核心。 -
n_jobs=-1:使用所有可用的 CPU 核心。 -
n_jobs=2:使用 2 个核心。
-
-
何时有用:
-
这个参数主要在目标值
y是多维(例如,你同时要预测多个相关的目标变量)时才会生效。对于绝大多数单目标回归问题(y是一维向量),设置n_jobs不会有任何性能提升,因为计算无法被并行化。
-
-
如何选择:
-
对于普通的房价预测等单目标问题,可以忽略此参数,保持默认
None即可。 -
只有在进行多输出回归(Multi-output Regression)时,才考虑设置
n_jobs=-1来加速。
-
4. positive : bool, default=False
-
功能:强制所有系数($w_1, w_2, ..., w_n$)为非负数。
-
详解:
-
positive=False(默认):系数可以是任意实数(正数、负数或零)。 -
positive=True:约束所有系数 >= 0。这相当于在求解最优化问题时增加了一个约束条件。
-
-
应用场景:
-
当你根据业务逻辑或先验知识,确定特征与目标之间只能是正相关关系时。例如,在商品需求预测中,假设价格打折(折扣力度是一个特征)永远不会导致需求减少,那么就可以强制该特征的系数为非负。
-
它也可以作为一种正则化的形式,帮助防止过拟合,特别是在特征数量多或数据量小的情况下。
-
-
如何选择:
-
大多数情况下保持默认
False。 -
只有当你有明确的理由要求模型系数必须为正时,才设置为
True。
-
线性回归-梯度下降使用 SGDRegressor
SGDRegressor 的参数可以分为几大类:损失函数、正则化、学习率和迭代控制。
sklearn.linear_model.SGDRegressor(loss='squared_error', penalty='l2', alpha=0.0001, l1_ratio=0.15,fit_intercept=True,max_iter=1000,tol=1e-3,shuffle=True,learning_rate='invscaling',eta0=0.01,power_t=0.25,early_stopping=False,validation_fraction=0.1,n_iter_no_change=5,epsilon=0.1,random_state=None,verbose=0,warm_start=False,
)参数详解:
1. 损失函数相关参数 (loss)
-
loss : str, default='squared_error'
-
功能:指定要使用的损失函数,即要最小化的目标函数。
-
可选值:
-
'squared_error':普通最小二乘,即线性回归。损失函数为 $(y - \hat{y})^2$。这是最常用的默认值。 -
'huber':Huber 损失,对异常值的敏感度低于平方损失。它是平方损失和绝对损失的结合,需要通过epsilon参数控制其敏感度。 -
'epsilon_insensitive':ε-不敏感损失,用于支持向量回归(SVR)。 -
'squared_epsilon_insensitive':平方的 ε-不敏感损失。
-
-
选择指南:
-
数据干净,无明显异常值:
'squared_error'。 -
数据中有异常值,希望模型更稳健:
'huber'并调整epsilon。
-
-
-
epsilon : float, default=0.1
-
功能:当
loss='huber'或'epsilon_insensitive'时,此参数决定了其对错误的容忍度。对于 Huber 损失,误差小于epsilon时是平方项,大于时是线性项。值越大,对异常值越不敏感。
-
2. 正则化相关参数 (penalty, alpha, l1_ratio)
这是 SGDRegressor 非常强大的一部分,你可以轻松实现多种正则化。
-
penalty : {'l2', 'l1', 'elasticnet'}, default='l2'
-
功能:指定使用的正则化类型,用于防止过拟合。
-
可选值:
-
'l2'(默认): Ridge 回归。惩罚系数大小的平方和。倾向于产生小而分散的系数。 -
'l1': Lasso 回归。惩罚系数大小的绝对值和。倾向于产生稀疏模型(许多系数为0),可用于特征选择。 -
'elasticnet': Elastic-Net。L1 和 L2 惩罚的凸组合。通过l1_ratio参数控制混合比例。 -
None: 无正则化。
-
-
-
alpha : float, default=0.0001
-
功能:正则化项的强度。乘以损失函数的常数。
-
详解:alpha 越大,正则化越强,模型系数会被压缩得越小(趋向于0),模型越简单,越可能欠拟合。
alpha越小,正则化越弱,模型更可能过拟合。 -
注意:SGD 中的
alpha等价于Ridge(alpha=alpha)和Lasso(alpha=alpha)中的alpha。这是最重要的需要调优的参数之一,通常通过网格搜索(如GridSearchCV)在[1e-5, 1e-4, ..., 1, 10]这样的范围内寻找最佳值。
-
-
l1_ratio : float, default=0.15
-
功能:当
penalty='elasticnet'时,Elastic-Net 混合参数。 -
详解:
-
l1_ratio = 0: 等价于 L2 惩罚。 -
0 < l1_ratio < 1: 混合 L1 和 L2。 -
l1_ratio = 1: 等价于 L1 惩罚。
-
-
3. 学习率调度参数 (learning_rate, eta0, power_t)
梯度下降中,学习率决定了每一步更新的步长。
-
learning_rate : str, default='invscaling'
-
功能:学习率调度策略。
-
可选值:
-
'constant': 恒定学习率,由eta0指定。eta = eta0 -
'optimal': 基于原始论文的启发式选择,不需要调eta0。 -
'invscaling'(默认): 逐渐衰减的学习率。计算公式为eta = eta0 / pow(t, power_t),其中t是时间步(迭代次数)。这是最常用的策略,随着迭代进行,步长越来越小,有助于收敛。 -
'adaptive': 自适应学习率。只要损失持续下降,就保持eta0不变;当连续n_iter_no_change次迭代损失下降低于tol时,将学习率除以5。
-
-
-
eta0 : float, default=0.01
-
功能:初始学习率。当
learning_rate为'constant','invscaling'或'adaptive'时使用。 -
详解:学习率设置太大可能导致算法无法收敛(在最优值附近震荡甚至发散),设置太小则收敛速度过慢。0.01 是一个常见的起始点。
-
-
power_t : float, default=0.25
-
功能:当
learning_rate='invscaling'时,用于计算学习率的指数。
-
4. 迭代与停止条件参数 (max_iter, tol, early_stopping)
-
max_iter : int, default=1000
-
功能:遍历训练数据的最大次数(epochs)。
-
详解:SGD 是迭代算法,需要一个停止条件。对于中小型数据集,1000 通常足够。如果数据集很大,可能需要减少这个值。
-
-
tol : float, default=1e-3
-
功能:停止训练的容忍度。
-
详解:如果一次迭代中损失的下降小于
tol,且early_stopping=False,则训练停止。调低 tol 可能会使模型拟合得更好,但也会增加训练时间。
-
-
early_stopping : bool, default=False
-
功能:是否使用提前停止。
-
详解:当设置为
True时,会预留一部分数据(validation_fraction)作为验证集。当验证分数在连续n_iter_no_change次迭代中没有提高至少tol时,就停止训练。这是一种有效防止过拟合的方法。
-
-
n_iter_no_change : int, default=5
-
功能:在提前停止或学习率自适应下降之前,等待验证集分数无改进的迭代次数。
-
-
validation_fraction : float, default=0.1
-
功能:当
early_stopping=True时,用作验证集的训练数据比例。
-
5. 其他重要参数
-
shuffle : bool, default=True
-
功能:是否在每轮迭代后打乱训练数据。强烈建议保持 True,打乱数据是 SGD 工作的核心假设之一,可以防止循环出现不良的更新模式。
-
-
random_state : int, default=None
-
功能:控制数据打乱和初始化的随机种子。设置一个固定的值可以确保每次运行的结果一致,对于复现实验结果至关重要。
-
-
warm_start : bool, default=False
-
功能:如果设为
True,那么调用fit()时会使用上一次训练得到的系数作为初始化参数,从而实现增量训练。否则,每次fit()都会重新初始化。
-
6,具体示例-加州房价预测
加州房价数据集介绍
-
数据集概况
-
来源:该数据集源自 1990 年的加州人口普查。
-
用途:用于回归模型的练习和测试,目标是预测加州各区域的房屋中位价。
-
样本数量:20,640 条记录。这比波士顿数据集(506条)大得多,能更好地体现机器学习算法的效果。
-
特征数量:8 个数值型特征。这些特征涵盖了人口、地理位置和经济指标。
-
目标变量:
MedHouseVal- 街区群体的房屋中位价,单位是十万美元。
注意:目标变量是分组中位价。这意味着一个街区的所有房屋都被分配了该街区的 median house value。对于任何位于该街区的房屋,目标值都是相同的。
-
特征详细说明
这8个特征提供了预测房价的不同维度信息,均无伦理问题:
-
MedInc:街区居民的收入中位数。
-
HouseAge:街区内房屋年龄中位数。
-
AveRooms:平均房间数(每户)。
-
AveBedrms:平均卧室数(每户)。
-
Population:街区人口数。
-
AveOccup:平均家庭成员数(每户)。
-
Latitude:街区的纬度。
-
Longitude:街区的经度。
3.目标变量:
-
MedHouseVal:房屋中位价(单位:十万美元)。
线性回归-正规方程使用 LinearRegression
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 1,加载数据
california = fetch_california_housing()
print(california.data, california.data.shape)
print(california.target)
print(california.feature_names)
# 2,数据预处理
X_train, X_test, y_train, y_test = train_test_split(california.data, california.target, test_size=0.2, random_state=20)
scaler = StandardScaler() # 数据标准化:消除不同特征量纲的影响
X_train_scaled = scaler.fit_transform(X_train) # fit计算生成模型,transform通过模型转换数据
X_test_scaled = scaler.transform(X_test) # # 使用训练集的参数转换测试集
# 3,创建和训练线性回归模型(正规方程)
lr_model = LinearRegression() # 创建分类器实例
lr_model.fit(X_train_scaled, y_train) # 训练模型
print('权重系数:', lr_model.coef_)
print('偏置值:', lr_model.intercept_) # 在线性回归模型中,•偏置(截距)•(bias)是模型参数之一,表示当所有特征值为0时,目标变量的期望值。
# 4,模型评估
y_predict = lr_model.predict(X_test_scaled)
print('预测值:', y_predict)
mse = mean_squared_error(y_test, y_predict)
print('正规方程-均方误差:', mse)运行输出:
[[ 8.3252 41. 6.98412698 ... 2.5555555637.88 -122.23 ][ 8.3014 21. 6.23813708 ... 2.1098418337.86 -122.22 ][ 7.2574 52. 8.28813559 ... 2.8022598937.85 -122.24 ]...[ 1.7 17. 5.20554273 ... 2.325635139.43 -121.22 ][ 1.8672 18. 5.32951289 ... 2.1232091739.43 -121.32 ][ 2.3886 16. 5.25471698 ... 2.6169811339.37 -121.24 ]] (20640, 8)
[4.526 3.585 3.521 ... 0.923 0.847 0.894]
['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude']
权重系数: [ 0.83275185 0.1173856 -0.27597663 0.29900186 -0.00795271 -0.03963673-0.88241635 -0.85338011]
偏置值: 2.0678235537788865
预测值: [1.58299034 3.01567949 1.75417605 ... 1.84161594 2.81049138 1.16693905]
正规方程-均方误差: 0.5410055769085323
Process finished with exit code 0线性回归-梯度下降使用 SGDRegressor
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 1,加载数据
california = fetch_california_housing()
print(california.data, california.data.shape)
print(california.target)
print(california.feature_names)
# 2,数据预处理
X_train, X_test, y_train, y_test = train_test_split(california.data, california.target, test_size=0.2, random_state=20)
scaler = StandardScaler() # 数据标准化:消除不同特征量纲的影响
X_train_scaled = scaler.fit_transform(X_train) # fit计算生成模型,transform通过模型转换数据
X_test_scaled = scaler.transform(X_test) # # 使用训练集的参数转换测试集
# 3,创建和训练线性回归模型(梯度下降)
lr_model = SGDRegressor() # 创建分类器实例
lr_model.fit(X_train_scaled, y_train) # 训练模型
print('权重系数:', lr_model.coef_)
print('偏置值:', lr_model.intercept_) # 在线性回归模型中,•偏置(截距)•(bias)是模型参数之一,表示当所有特征值为0时,目标变量的期望值。
# 4,模型评估
y_predict = lr_model.predict(X_test_scaled)
print('预测值:', y_predict)
mse = mean_squared_error(y_test, y_predict)
print('梯度下降方程-均方误差:', mse)运行输出:
[[ 8.3252 41. 6.98412698 ... 2.5555555637.88 -122.23 ][ 8.3014 21. 6.23813708 ... 2.1098418337.86 -122.22 ][ 7.2574 52. 8.28813559 ... 2.8022598937.85 -122.24 ]...[ 1.7 17. 5.20554273 ... 2.325635139.43 -121.22 ][ 1.8672 18. 5.32951289 ... 2.1232091739.43 -121.32 ][ 2.3886 16. 5.25471698 ... 2.6169811339.37 -121.24 ]] (20640, 8)
[4.526 3.585 3.521 ... 0.923 0.847 0.894]
['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude']
权重系数: [ 9.00030244e-01 1.20593849e-01 -5.13860669e-01 2.43337638e-01-5.14784939e-04 -1.24408200e-01 -7.15071233e-01 -6.91217595e-01]
偏置值: [2.05038682]
预测值: [1.67351153 2.91473399 1.719945 ... 1.93827611 2.66340199 1.29512693]
梯度下降方程-均方误差: 0.7115888243566497,回归性能评估
均方误差(Mean Squared Error,MSE)是回归问题中常用的性能评估指标之一,它衡量了模型预测值与真实值之间的差异。MSE的公式如下:
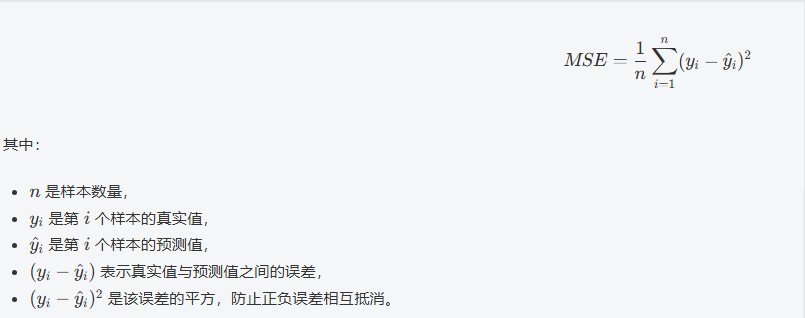
在 scikit-learn 中,计算均方误差非常简单,可以通过 mean_squared_error 函数来实现:
mean_squared_error(y_true, y_pred, *, sample_weight=None, multioutput='uniform_average', squared=True
)参数详解:
1. y_true : array-like of shape (n_samples,) or (n_samples, n_outputs)
-
功能:真实值(Ground Truth / Actual Values)。
-
要求:这是必需的定位参数(必须提供)。
-
格式:可以是一维数组(单输出问题)或二维数组(多输出问题)。
2. y_pred : array-like of shape (n_samples,) or (n_samples, n_outputs)
-
功能:预测值(Predicted Values)。
-
要求:这是必需的定位参数(必须提供)。
-
格式:必须与
y_true具有相同的形状。
3. sample_weight : array-like of shape (n_samples,), default=None
-
功能:样本权重。用于给每个样本的损失赋予不同的重要性。
-
详解:
-
None(默认):所有样本的权重相等。 -
提供权重数组:权重大的样本,其预测误差对最终 MSE 的贡献也更大。
-
-
应用场景:
-
某些样本在业务上更重要,需要模型更准确地预测它们。
-
处理类别不平衡的回归问题(虽然不常见)。
-
