MATLAB基本运算(2)
MATLAB基本运算概述
MATLAB提供了丰富的运算功能,包括算术运算、关系运算、逻辑运算以及数学函数。这些运算可以直接作用于标量、向量、矩阵或更高维数组。
算术运算
MATLAB支持标准的算术运算符,遵循矩阵运算规则:
加法:
+A + B % 矩阵对应元素相加减法:
-A - B % 矩阵对应元素相减乘法:
*A * B % 矩阵乘法(非对应元素相乘)除法:
/和\A / B % 近似等于A*inv(B) A \ B % 近似等于inv(A)*B幂运算:
^A^2 % 矩阵A的平方点运算(对应元素运算):
.,./,.*,.^A .* B % 对应元素相乘 A ./ B % 对应元素相除 A .^ 2 % 每个元素平方
关系运算
关系运算符返回逻辑值(true或false):
等于:
==A == B % 判断对应元素是否相等不等于:
~=A ~= B % 判断对应元素是否不等大于:
>A > B % 判断对应元素是否大于小于:
<A < B % 判断对应元素是否小于大于等于:
>=A >= B % 判断对应元素是否大于等于小于等于:
<=A <= B % 判断对应元素是否小于等于
逻辑运算
逻辑运算符用于组合或操作逻辑值:
与:
&或&&A & B % 元素级逻辑与 A && B % 标量逻辑与(短路运算)或:
|或||A | B % 元素级逻辑或 A || B % 标量逻辑或(短路运算)非:
~~A % 逻辑非异或:
xorxor(A, B) % 逻辑异或
数学函数
MATLAB提供了丰富的内置数学函数:
基本数学函数:
abs(x) % 绝对值 sqrt(x) % 平方根 exp(x) % 指数函数 log(x) % 自然对数 log10(x) % 常用对数三角函数:
MATLAB中余弦函数的输入方式
在MATLAB中计算余弦值,需注意角度与弧度的转换。默认情况下,
cos函数接受弧度作为输入。要计算70度的余弦值,需将角度转换为弧度或使用专门的角度函数。使用
cosd函数直接输入角度MATLAB提供了
cosd函数,可直接输入角度值进行计算:result = cosd(70); % 计算70度的余弦值使用
cos函数结合弧度转换若需使用
cos函数,需先将角度转换为弧度。转换公式为:
弧度 = 角度 × π / 180
对应的MATLAB代码为:radians = 70 * pi / 180; % 将70度转换为弧度 result = cos(radians); % 计算余弦值验证计算结果
为验证两种方法的结果一致性,可运行以下代码:
cosd_result = cosd(70); cos_result = cos(70 * pi / 180); disp(['cosd(70): ', num2str(cosd_result)]); disp(['cos(70° in radians): ', num2str(cos_result)]);输出应显示相同的结果(约0.3420)。
注意事项
- 函数选择:优先使用
cosd简化角度计算。 - 精度问题:浮点数计算可能存在微小差异,但在实际应用中可忽略。
- 其他三角函数:类似地,
sind、tand等函数也支持直接角度输入。 取整函数:
round(x) % 四舍五入 floor(x) % 向下取整 ceil(x) % 向上取整 fix(x) % 向零取整复数运算:
real(z) % 实部 imag(z) % 虚部 angle(z) % 相位角 conj(z) % 共轭复数统计函数:
max(A), min(A) % 最大值/最小值 mean(A) % 平均值 median(A) % 中位数 std(A) % 标准差矩阵运算函数:
det(A) % 行列式 inv(A) % 逆矩阵 eig(A) % 特征值 rank(A) % 矩阵秩
这些运算和函数可以组合使用,构建复杂的数学表达式和算法。MATLAB的向量化特性使得这些运算能够高效地作用于整个数组,无需显式循环。
1求下列表达式的值。
x=1+2×cos(π)+3i
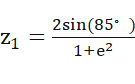
2,设三个复数a=3+4i,b=1+2i,c=2e![]() ,计算x=ab/c。
,计算x=ab/c。
我们需要用得到点乘和三角函数输入,指数函数的输入:
1;(1)
x=1+2*cos(pi)+3i //这里我们用的Π为pi;
(2)
z=2*sind(85)/1+exp(2) //这里用到三角函数直接输入数字度数和指数函数
2:
a=3+4i;b=1+2i;c=2*exp(pi*i/6);x=a*b/c书写代码都是英文输入;注意分号和逗号的区分使用。
MATLAB中逗号与分号的区别
逗号(,)的主要用途
- 分隔数组或矩阵中的元素:
A = [1, 2, 3]; % 定义行向量,逗号分隔元素 - 分隔函数输入参数:
max(A, B); % 逗号分隔函数的多个输入参数 - 分隔同一行的多条命令:
a = 1, b = 2; % 逗号分隔两条赋值语句,均显示结果
分号(;)的主要用途
- 抑制命令行的输出显示:
C = [1; 2; 3]; % 定义列向量,分号分隔元素且不显示结果 - 分隔矩阵的行:
D = [1, 2; 3, 4]; % 分号分隔矩阵的不同行 - 分隔多行命令(不显示中间结果):
x = 1; y = 2; % 分号分隔命令且不显示赋值结果
关键区别总结
- 输出控制:逗号允许显示结果,分号抑制输出。
- 矩阵构造:逗号分隔同一行元素,分号分隔不同行。
- 代码风格:分号常用于脚本中减少冗余输出,逗号用于交互式调试时查看中间值。
示例对比:
% 逗号示例:显示所有结果
A = 1, B = 2, C = A + B % 分号示例:仅显示最后结果
A = 1; B = 2; C = A + B
