当前位置：首页 > news >正文

随机梯度下降（SGD）算法及其在机器学习中的应用

news 2025/9/21 5:51:58

随机梯度下降（SGD）算法及其在机器学习中的应用

随机梯度下降（SGD）是一种高效的优化方法，适用于大规模数据的回归和分类任务。本文介绍了 SGD 的算法原理、数学模型、实现流程及参数解析，并通过 Python scikit-learn 案例展示其在回归（加州房价预测）与分类（鸢尾花分类）中的应用与可视化效果。

1. 算法介绍

随机梯度下降（Stochastic Gradient Descent，简称 SGD）是一种常见的优化方法，主要用于解决大规模机器学习中的参数更新问题。
与传统的批量梯度下降（Batch Gradient Descent）不同，SGD 并不是在所有样本上计算整体损失的梯度，而是在每次迭代时仅用一个或小批量样本更新参数，从而显著提高计算效率。

SGD 常用于：

线性回归、逻辑回归等线性模型的训练
支持向量机（SVM）的优化
神经网络的参数更新

其核心思想是：以较小的计算代价，逐步逼近最优解。

2. 数学模型

假设我们有训练数据集
$\mathcal{D} = \{ (x_i, y_i) \}_{i=1}^n$
其中 $xi∈Rdx_i \in \mathbb{R}^d$ 表示特征， $y_i$ 表示标签。

模型参数为 $θ\theta$ ，损失函数为 $L(θ;xi,yi)L(\theta; x_i, y_i)$ 。

目标是最小化经验风险：
$J(\theta) = \frac{1}{n} \sum_{i=1}^{n} L(\theta; x_i, y_i)$
梯度下降法更新公式：
$\theta^{(t+1)} = \theta^{(t)} - \eta \nabla_\theta J(\theta^{(t)})$
随机梯度下降更新公式：
$\theta^{(t+1)} = \theta^{(t)} - \eta \nabla_\theta L(\theta^{(t)}; x_i, y_i)$
其中 $η\eta$ 为学习率，每次迭代随机抽取一个样本 $x_i, y_i)$ 来更新参数。

3. 实现流程

初始化：随机初始化参数 $θ\theta$
循环迭代：
- 从训练集中随机选取一个样本 $x_i, y_i)$
- 计算当前样本的损失函数梯度
- 按更新公式调整参数
收敛判断：迭代直到损失函数趋于稳定或达到设定的迭代次数

4. SGD 主要参数解析

4.1 SGD 回归器（`SGDRegressor`）

SGDRegressor(loss='squared_error',     # 损失函数类型，线性回归常用 squared_error；可选 'huber', 'epsilon_insensitive' 等鲁棒回归损失penalty='l2',             # 正则化方式：'l2'（岭回归）、'l1'（LASSO）、'elasticnet'（混合）alpha=0.0001,             # 正则化强度，越大正则化越强l1_ratio=0.15,            # L1/L2 比例，仅 penalty='elasticnet' 时生效fit_intercept=True,       # 是否学习截距项max_iter=1000,            # 最大迭代轮数tol=0.001,                # 提前停止的容忍度shuffle=True,             # 每轮是否打乱训练数据random_state=None,        # 随机种子，保证可复现learning_rate='invscaling', # 学习率策略：'constant', 'invscaling', 'adaptive'eta0=0.01,                # 初始学习率power_t=0.25,             # 学习率衰减指数，仅 'invscaling' 生效early_stopping=False,     # 是否启用早停validation_fraction=0.1,  # 验证集比例，仅早停启用时生效n_iter_no_change=5,       # 连续多少轮验证集未改善则提前停止warm_start=False,         # 是否在上次训练基础上继续训练average=False,            # 是否使用平均 SGD（ASGD）
)

核心控制模型复杂度：alpha、penalty、l1_ratio、fit_intercept

防止过拟合：early_stopping、n_iter_no_change、validation_fraction

学习率与训练控制：learning_rate、eta0、power_t、max_iter、shuffle

4.2 SGD 分类器（`SGDClassifier`）

SGDClassifier(loss='hinge',             # 损失函数类型，分类常用 'hinge'（SVM），'log_loss'（逻辑回归），'modified_huber' 更鲁棒penalty='l2',             # 正则化方式：'l2', 'l1', 'elasticnet'alpha=0.0001,             # 正则化强度l1_ratio=0.15,            # L1/L2 比例，仅 penalty='elasticnet' 时生效fit_intercept=True,       # 是否学习截距max_iter=1000,            # 最大迭代轮数tol=0.001,                # 提前停止容忍度shuffle=True,             # 每轮是否打乱训练数据random_state=None,        # 随机种子learning_rate='optimal',  # 学习率策略：'optimal', 'constant', 'invscaling', 'adaptive'eta0=0.0,                 # 初始学习率power_t=0.5,              # 学习率衰减指数，仅 'invscaling' 生效early_stopping=False,     # 是否启用早停validation_fraction=0.1,  # 验证集比例n_iter_no_change=5,       # 连续验证集未改善轮数class_weight=None,        # 类别权重，None 或 'balanced' 或字典warm_start=False,         # 是否继续上一次训练average=False,            # 是否使用平均 SGD（ASGD）
)

核心控制模型复杂度：alpha、penalty、l1_ratio、fit_intercept

防止过拟合：early_stopping、n_iter_no_change、validation_fraction、class_weight

学习率与训练控制：learning_rate、eta0、power_t、max_iter、shuffle

4.3 SGD 回归 vs 分类 — 参数差异对照表

参数	SGDRegressor	SGDClassifier	说明
loss	`'squared_error'`（默认）；可选 `'huber'`, `'epsilon_insensitive'`	`'hinge'`（默认）；可选 `'log_loss'`, `'modified_huber'`	损失函数，决定优化目标
learning_rate	默认 `'invscaling'`	默认 `'optimal'`	学习率策略
eta0	默认 0.01	默认 0.0	初始学习率
power_t	默认 0.25	默认 0.5	学习率衰减指数
class_weight	不适用	可设置类别权重	分类任务特有

绝大多数参数（如 penalty, alpha, l1_ratio, fit_intercept, max_iter, tol, shuffle 等）在回归和分类中相同。

差异点：

分类任务有 class_weight；回归任务有更多损失函数选项。
学习率默认策略不同：分类更稳健，回归更适合连续优化。

5. 实例演示

这里我们以 加州房价数据集（回归任务） 和 鸢尾花数据集（分类任务） 为例，展示 SGD 的应用。

5.1 导入Python库

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from sklearn.datasets import load_iris, fetch_california_housing
from sklearn.linear_model import SGDClassifier, SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score, mean_squared_error, r2_score# 设置 Seaborn 风格（中文支持 + 负号显示正常）
sns.set_theme(style="whitegrid", font="Microsoft YaHei", rc={"axes.unicode_minus": False})

5.2 回归：使用 `SGDRegressor` 预测房价

# =================== 回归任务：加州房价 ===================
housing = fetch_california_housing()
X, y = housing.data, housing.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)reg = SGDRegressor(loss="squared_error", max_iter=1000, tol=1e-3, random_state=42)
reg.fit(X_train, y_train)y_pred = reg.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
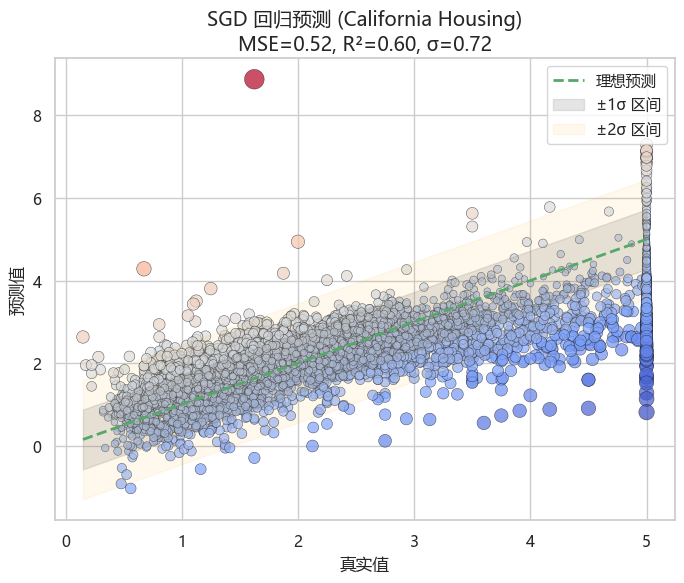
r2 = r2_score(y_test, y_pred)# 回归预测效果可视化
plt.figure(figsize=(8, 6))# 真实 vs 预测散点（颜色 = 误差大小，点大小 = 误差幅度）
sns.scatterplot(x=y_test, y=y_pred, hue=y_pred - y_test, palette="coolwarm",size=np.abs(y_pred - y_test), sizes=(20, 200),alpha=0.7, edgecolor="k", legend=False)# 理想预测线
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()],"g--", lw=2, label="理想预测")# 计算残差标准差
residuals = y_pred - y_test
sigma = np.std(residuals)# 误差带 ±σ 和 ±2σ
x_range = np.linspace(y_test.min(), y_test.max(), 200)
plt.fill_between(x_range, x_range - sigma, x_range + sigma,color="gray", alpha=0.2, label="±1σ 区间")
plt.fill_between(x_range, x_range - 2*sigma, x_range + 2*sigma,color="orange", alpha=0.07, label="±2σ 区间")plt.xlabel("真实值", fontsize=12)
plt.ylabel("预测值", fontsize=12)
plt.title(f"SGD 回归预测 (California Housing)\nMSE={mse:.2f}, R²={r2:.2f}, σ={sigma:.2f}", fontsize=14)
plt.legend()
plt.show()

download

5.3 分类：使用 `SGDClassifier` 训练线性分类器

# =================== 分类任务：鸢尾花 ===================
iris = load_iris()
X, y = iris.data[:, :2], iris.target  # 仅取前两个特征便于可视化
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)clf = SGDClassifier(loss="hinge", max_iter=1000, tol=1e-3, random_state=42)
clf.fit(X_train, y_train)y_pred = clf.predict(X_test)
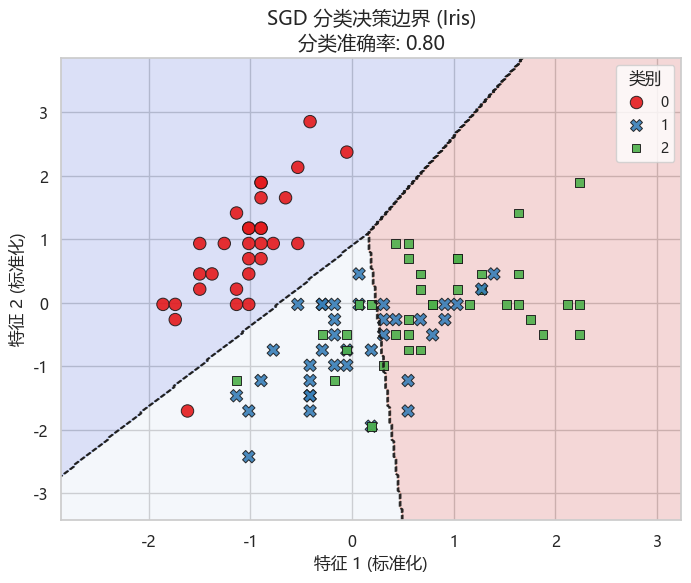
acc = accuracy_score(y_test, y_pred)# 决策边界可视化
xx, yy = np.meshgrid(np.linspace(X_train[:, 0].min()-1, X_train[:, 0].max()+1, 300),np.linspace(X_train[:, 1].min()-1, X_train[:, 1].max()+1, 300))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)plt.figure(figsize=(8, 6))
# 区域背景填充（淡色）
plt.contourf(xx, yy, Z, alpha=0.2, cmap="coolwarm")
# 决策边界线
plt.contour(xx, yy, Z, colors="k", linewidths=1, linestyles="--", alpha=0.7)
# 训练样本散点
sns.scatterplot(x=X_train[:, 0], y=X_train[:, 1], hue=y_train, style=y_train,palette="Set1", s=80, edgecolor="k", alpha=0.9, legend="full")
plt.title(f"SGD 分类决策边界 (Iris)\n分类准确率: {acc:.2f}", fontsize=14)
plt.xlabel("特征 1 (标准化)", fontsize=12)
plt.ylabel("特征 2 (标准化)", fontsize=12)
plt.legend(title="类别", fontsize=10)
plt.show()