数据结构(1)------ 三要素
目录
1、数据结构三要素
1.1、逻辑结构
1.1.1、集合(不重要)
1.1.2、线性结构
1.1.3、树型结构
1.1.4、图结构
1.2、数据运算
1.3、数据的物理(存储)结构
1.3.1、顺序储存
1.3.2、链式存储
1.3.3、索引存储
1.3.4、散列存储
2、算法
2.1、算法特性
2.2、“好”算法特性
2.3、算法时间复杂度
2.3.1、例子
2.3.2、计算规则
2.4、空间复杂度
2.4.1、例子
1、数据结构三要素
1.1、逻辑结构
1.1.1、集合(不重要)
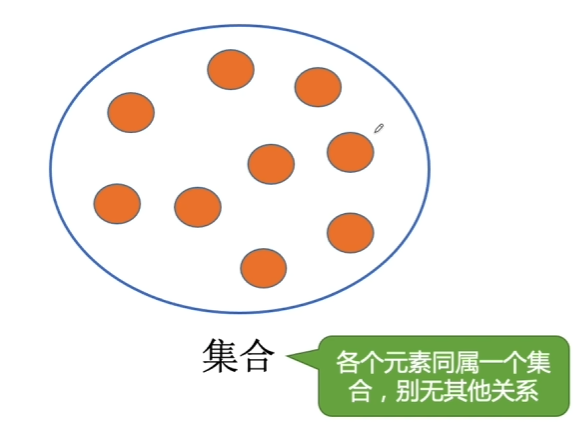
eg.
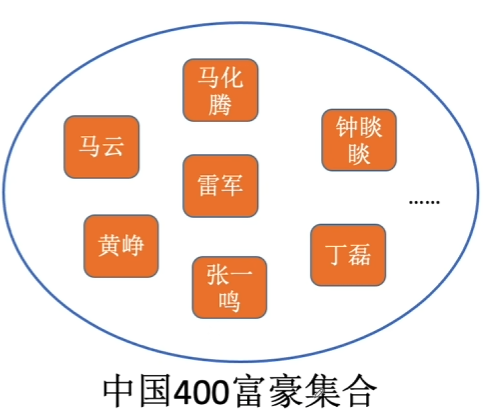
1.1.2、线性结构
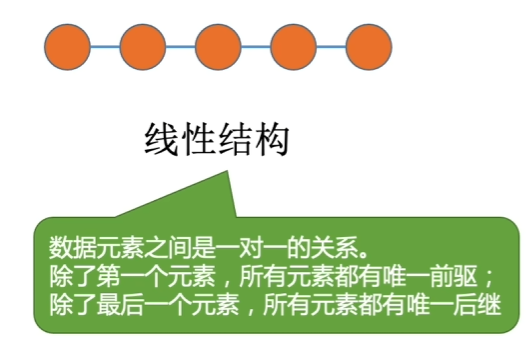
1.1.3、树型结构
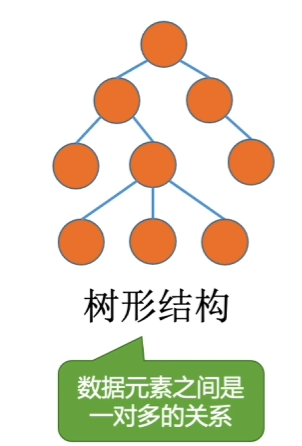
eg.
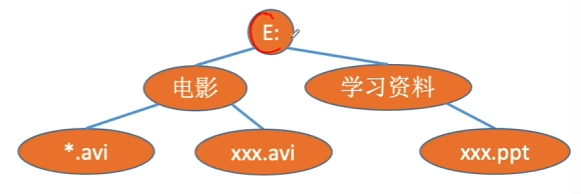
1.1.4、图结构
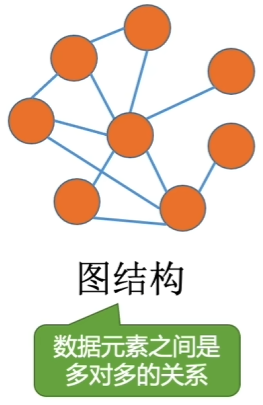
eg.
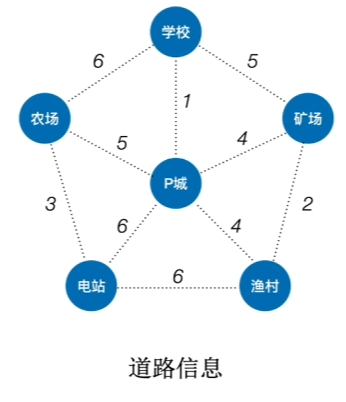
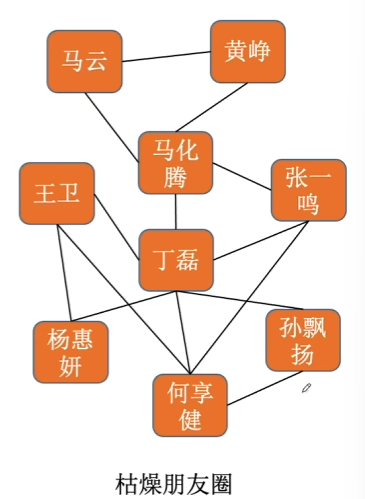
1.2、数据运算
针对某种逻辑结构,结合实际需求,定义基本运算。
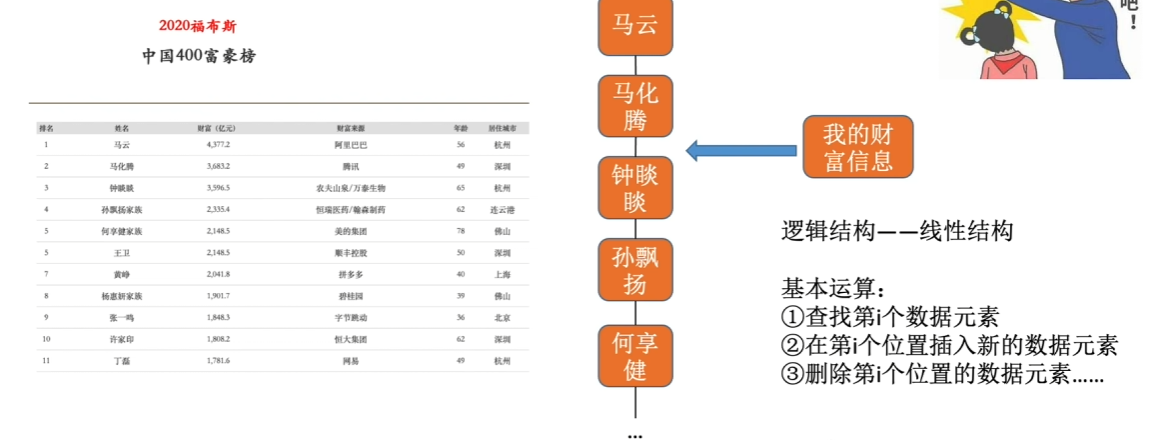
1.3、数据的物理(存储)结构
1.3.1、顺序储存
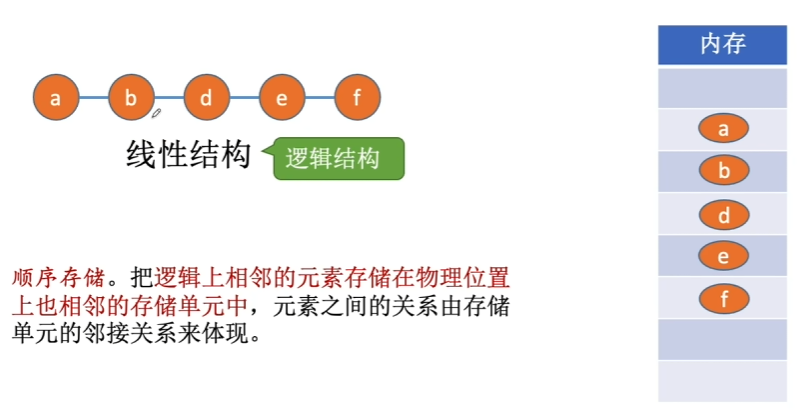
eg. 平常的数组存储数据;
1.3.2、链式存储
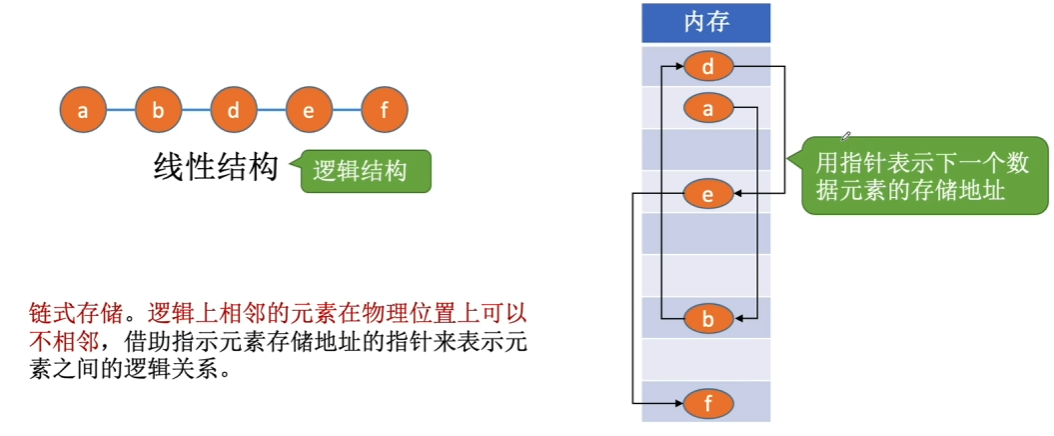
eg. FreeRtos中的 heap4 管理方式,通过指针将申请的内存,并将碎片化的内存合并;
1.3.3、索引存储
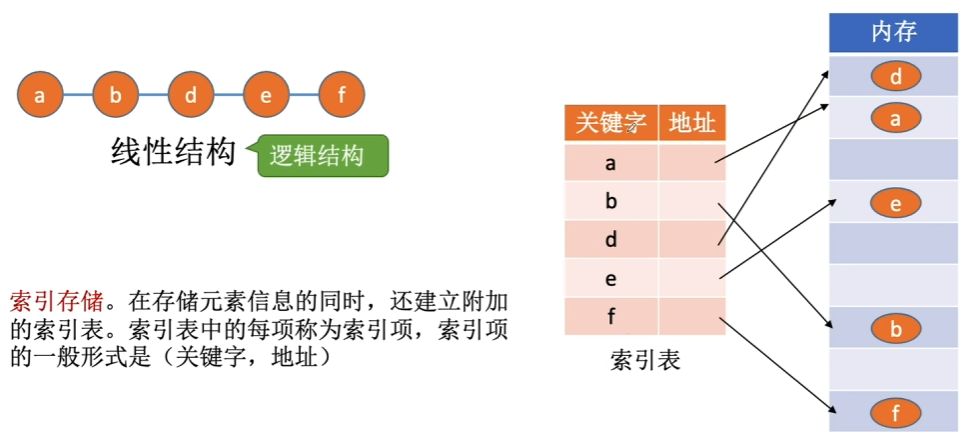
eg. 类似于CanOpen协议栈中的对象字典;
1.3.4、散列存储
![]() 具体后面章节介绍。
具体后面章节介绍。
2、算法
求解问题的步骤。(如:最简单的处理排序问题的排序算法)
2.1、算法特性
1、有穷性:算法必须总在执行有穷步之后结束,且每步都可在有穷时间内完成;
2、确定性:算法中每条指令必须有确切的含义,对于相同的输入只能得出相同的输出;
3、可行性:算法中描述的操纵都可以通过已经实现的基本运算执行有限次来实现;
4、输入:一个算法有0个或多个输入,这些取自于某个特定的对象的集合;
5、输出:一个算法有0个或多个输出,这些输出是与输入有着某种特定关系的量;
2.2、“好”算法特性
1、正确性:算法应该能够正确地解决求解问题;
2、可读性:算法应具有良好的可读性;
3、健壮性:输入非法数据时,算法能适应当地做出反应或进行处理,而不会产生莫名其妙的输出结果;
4、高效率与低存储量需求;
2.3、算法时间复杂度
评价算法的时间开销。
事前预估算法时间开销T(n)与问题规模n的关系(T表示“time”)
2.3.1、例子
这里将所有语句的时间都默认为一致,简化计算:
若T(n)的表达式很复杂,程序很冗长,上述统计的方法就不起作用了。这里就需要简化时间复杂度的表达式:



若n足够大,则可以忽略低阶的n带来的影响。可以只考虑高阶的部分。
2.3.2、计算规则
(a)加法规则
![]()
(b)乘法规则
![]()
Eg.
![]()
![]()
时间复杂度比较:
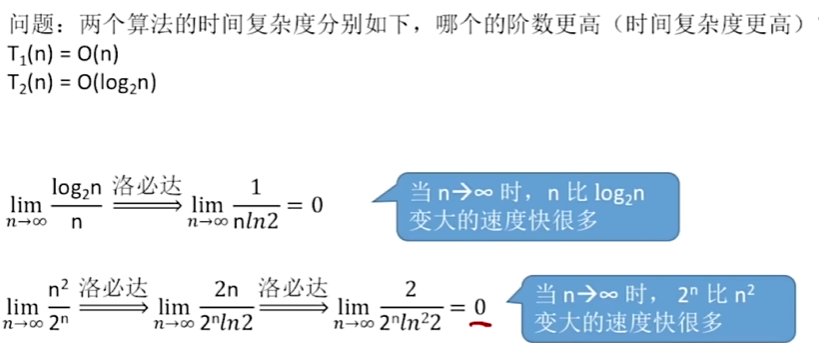
嵌套型时间复杂度:

指数型时间复杂度:

搜索数字爱你时间复杂度:

2.4、空间复杂度
空间开销与问题规模n之间的关系。
2.4.1、例子
1、算法所需的空间,和问题规模n没有关系
2、
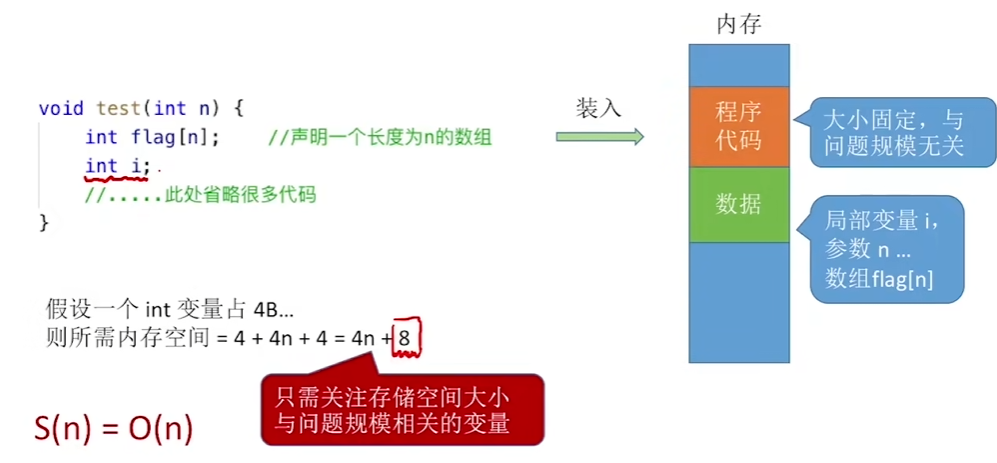
3、
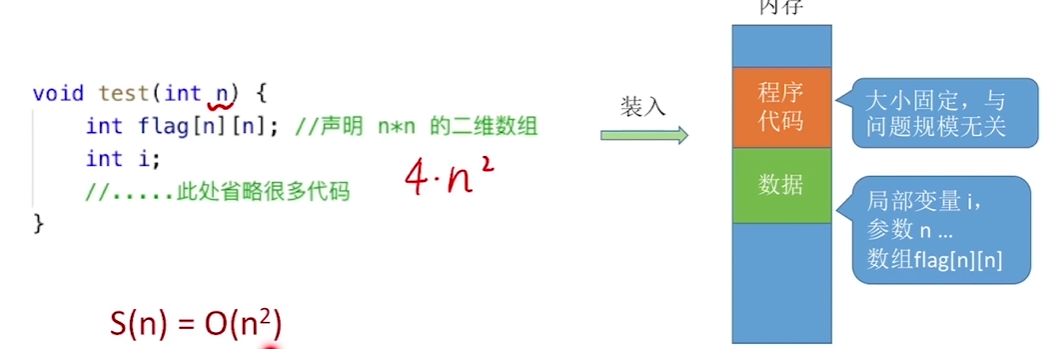
4、

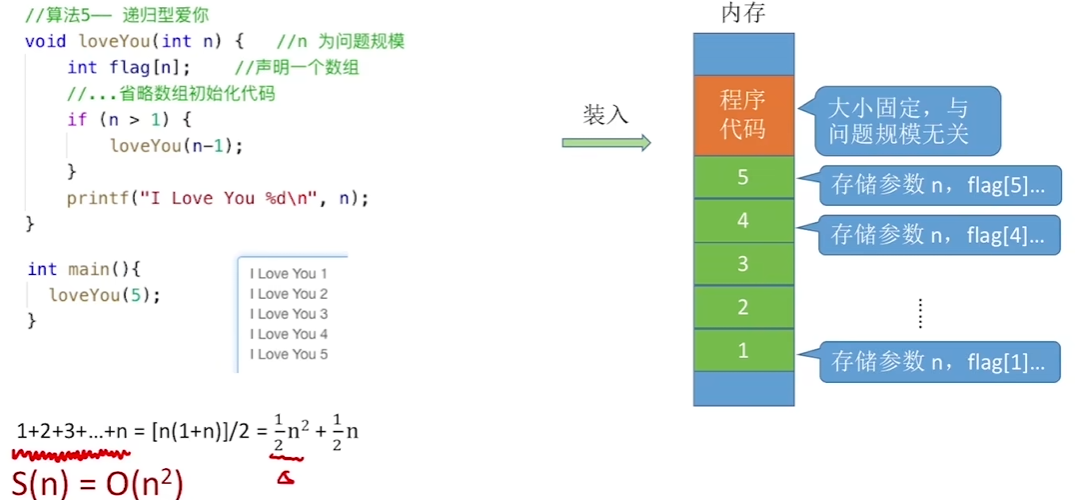
5、函数调用导致内存开销的情况(递归调用)
递归调用的层数且每次调用的空间不变,和n是一样的情况:
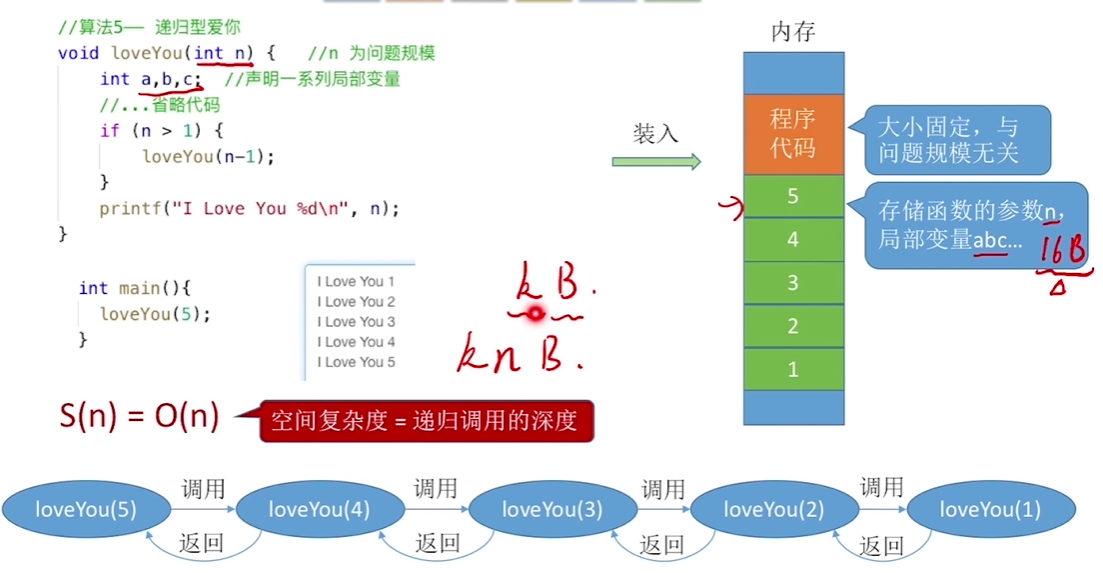
递归调用的层数且每次调用的空间随n变化: