离散数学之命题逻辑

每日一句
用最少的悔恨面对过往
用最少的挥霍面对现在
用最多的梦面对未来。

目录
每日一句
前言
一.命题:逻辑世界的 “基本单元”
1.命题的定义:能判断真假的陈述句
2.命题的分类:简单命题与复合命题
二.逻辑联结词:5 个 “角色” 记住核心定义
三.合式公式的类型与真值函数
1.真值表:命题逻辑的 “真值计算器” 与 “验证工具”
(1).真值表的核心构成:3 个关键部分
(2).真值表的制作步骤:4 步标准化流程
步骤 1:确定原子命题与组合数
步骤 2:拆解复合命题为 “子命题”
步骤 3:计算各子命题的真值
步骤 4:计算最终复合命题的真值
(3).真值表的核心用途:3 个关键场景
1. 验证公式等值:判断两个命题是否 “永远同真同假”
2. 判断命题类型:区分永真式、永假式、可满足式
3. 分析逻辑推理有效性:判断 “前提→结论” 是否为永真式
(4).注意事项:避免出错的 2 个关键点
2.合式公式的三种类型
重言式(永真式):永远为真的公式
矛盾式(永假式):永远为假的公式
可满足式:至少存在一种真值组合使公式为真
3.真值函数:公式与真值的对应关系
真值函数的个数:
公式与真值函数的关系:
四.逻辑等值公式:形象绑定,告别死记硬背
1. 双重否定律
E₁:¬¬P ⇔ P
2.等幂律:“重复运算” 的简化规则
E₂:P∨P ⇔ P
E₃:P∧P ⇔ P
3.交换律
E₄:P∨Q ⇔ Q∨P
E₅:P∧Q ⇔ Q∧P
4.结合律
E₆:(P∨Q)∨R ⇔ P∨(Q∨R)
E₇:(P∧Q)∧R ⇔ P∧(Q∧R)
5.分配律
E₈:P∧(Q∨R) ⇔ (P∧Q)∨(P∧R)
E₉:P∨(Q∧R) ⇔ (P∨Q)∧(P∨R)
6. 德摩根律
E₁₀:¬(P ∨ Q) ⇔ ¬P ∧ ¬Q
E₁₁:¬(P ∧ Q) ⇔ ¬P ∨ ¬Q
7.吸收律
E₁₂:P∨(P∧Q) ⇔ P
E₁₃:P∧(P∨Q) ⇔ P
8.零律与9.同一律
E₁₄:P∨1 ⇔ 1
E₁₅:P∧0 ⇔ 0
E₁₆:P∨0 ⇔ P
E₁₇:P∧1 ⇔ P
10.否定律
E₁₈:P∨¬P ⇔ 1
E₁₉:P∧¬P ⇔ 0
11. 蕴含等值式
E₂₀:P → Q ⇔ ¬P ∨ Q
12.等价等值式
E₂₁:P↔Q ⇔ (P→Q)∧(Q→P)
13. 逆否律
E₂₂:P → Q ⇔ ¬Q → ¬P
14.输出律
E₂₃:(P ∧ Q → R) ⇔ (P → (Q → R))
15.归谬论
E₂₄:(P→Q)∧(P→¬Q) ⇔ ¬P
总结:24 条公式的 “记忆优先级与关联逻辑”
五.全功能联结词:逻辑武器的 “最小套装”
1. 经典 “精简套装”:3 组常用组合
(1).想拼出 “P∨Q”(P 或 Q),利用德摩根律:P ∨ Q ⇔ ¬(¬P ∧ ¬Q)
(2).{¬, ∨}(非 + 或):用 “或” 和 “非” 拼出 “且”
(3).{¬, →}(非 + 蕴含):最接近数学推理的套装
2. 终极 “一件套装”:只用 1 个联结词,拼出全世界!
(1).与非(NAND):P ↑ Q ⇔ ¬(P ∧ Q)
(2).或非(NOR):P ↓ Q ⇔ ¬(P ∨ Q)
六.对偶原理:逻辑世界的 “镜面反射”
核心思想:逻辑公式的 “阴阳对称”
1. 如何制造 “对偶影子”?(操作口诀)
2. 对偶原理的 “买一送一” 魔力
总结
前言
在命题逻辑的学习中,逻辑联结词的定义是 “地基”,核心等值公式是 “承重墙”—— 只有把这两者牢牢记住,后续的公式化简、逻辑证明才能顺畅推进。下面我会用 “形象记忆锚点 + 口诀 + 应用场景” 的方式,帮你把这些核心内容刻进脑子里,避免死记硬背。
一.命题:逻辑世界的 “基本单元”
要理解逻辑联结词和公式,首先得明确 “命题” 这个起点 —— 它是构成所有逻辑表达式的 “最小积木”,没有清晰的命题定义,后续的逻辑运算就成了无本之木。
1.命题的定义:能判断真假的陈述句
严格来说,命题是具有唯一真值的陈述句,这意味着它必须同时满足两个核心条件:
条件 1:是陈述句:排除疑问句(“今天会下雨吗?”)、祈使句(“请打开窗户”)、感叹句(“天气真好啊!”),这类句子无法判断 “对或错”,因此不是命题。
条件 2:有唯一真值:要么为真(用 “1” 或 “T” 表示),要么为假(用 “0” 或 “F” 表示),不存在 “既真又假” 或 “无法确定” 的情况。
示例:“2 是偶数”(真值为 1)、“三角形有 4 条边”(真值为 0)都是命题;而 “x+1=3”(x 的值不确定,无法判断真假)、“未来人类会移民火星”(当前无法确定真值)暂不视为命题。
2.命题的分类:简单命题与复合命题
根据是否包含逻辑联结词,命题可分为两类,这也是后续学习的关键区分:
简单命题(原子命题):不包含任何逻辑联结词的 “单一陈述句”,是不可再拆分的基本单元。
示例:“太阳从东方升起”“小明喜欢数学”。通常用小写字母 p、q、r、s… 表示,比如用 p 表示 “2 是质数”,q 表示 “3 是偶数”。
复合命题:由多个简单命题通过 “逻辑联结词” 组合而成的命题,可拆分为简单命题和联结词两部分。
示例:“2 是质数,且 3 是奇数”(由 p “2 是质数”、q “3 是奇数” 通过 “且(∧)” 联结而成)、“如果明天放假,那么我去旅行”(由 p “明天放假”、q “我去旅行” 通过 “如果… 则…(→)” 联结而成)。
例题 1:命题符号化(将自然语言转化为逻辑表达式)
题目要求
用原子命题(p、q、r 等)表示下列自然语言,并写出对应的逻辑公式:
(1)小明既喜欢数学,又喜欢物理;
(2)今天下雨或刮风,但不打雷;
(3)如果明天不加班,我就去看电影或逛商场;
(4)四边形是平行四边形,当且仅当它的两组对边分别平行。解题步骤
1.定义原子命题(关键:拆分 “最小陈述句”,不包含逻辑联结词)
(1)设 p:小明喜欢数学;q:小明喜欢物理;
(2)设 p:今天下雨;q:今天刮风;r:今天打雷;
(3)设 p:明天加班;q:我去看电影;r:我逛商场;
(4)设 p:四边形是平行四边形;q:四边形的两组对边分别平行。
2.根据自然语言中的逻辑关系,选择联结词组合
(1)“既… 又…” 对应 “且(∧)”,公式:p ∧ q;
(2)“或(相容或)” 对应 “∨”,“但不” 对应 “∧ ¬”,公式:(p ∨ q) ∧ ¬r;
(3)“如果不… 就…” 对应 “¬p → (∨)”,“或” 对应 “∨”,公式:¬p → (q ∨ r);
(4)“当且仅当” 对应 “等价(↔)”,公式:p ↔ q。
思路提炼
符号化的核心是 “先拆原子命题,再找联结词”:
① 原子命题必须是 “能判断真假的单一陈述句”,避免包含 “且、或、如果” 等联结词;
② 注意自然语言的歧义:“或” 默认是 “相容或(∨)”(如 “下雨或刮风” 可同时发生),若明确 “要么… 要么…”(如 “要么去北京要么去上海”),需用 “排斥或((p∧¬q)∨(¬p∧q))”;
③ “如果 A 就 B” 统一转化为 “A→B”,“不 A” 转化为 “¬A”。
二.逻辑联结词:5 个 “角色” 记住核心定义
与其机械记符号和真值表,不如给每个联结词赋予一个 “专属形象”,让符号变成 “有故事的角色”,记忆会更深刻。
| 符号 | 名称 | 专属形象记忆(记忆锚点) | 决定性规则(口诀 + 真值关键) | 常见误区提醒 |
|---|---|---|---|---|
| ¬ | 非(否定) | 房间的单开开关:按一下开灯(状态 1→0),再按一下关灯(0→1),啪嗒两下就回到初始状态 | 一否就反,真假互换 (P 真则 ¬P 假,P 假则 ¬P 真) | 注意否定词的 “管辖范围”,比如 ¬(P∨Q) 是对整体否定,不是 ¬P∨Q |
| ∧ | 且(合取) | 电影院的严格门卫:查票时必须两个人都有票(P 真且 Q 真),才让进;少一个都不行 | 同真才真,一假则假 (只有 P=1、Q=1 时,P∧Q=1) | 日常语言中的 “并且” 可能有顺序,但逻辑中 P∧Q 和 Q∧P 完全等价 |
| ∨ | 或(析取) | 请客的大度朋友:只要有人来(P 真或 Q 真)就开心,两个人都来(P、Q 都真)更开心 | 有真就真,同假才假 (只有 P=0、Q=0 时,P∨Q=0) | 这里是 “相容或”(允许两者都真),不是 “排斥或”(要么 A 要么 B,不能都有) |
| → | 如果… 则…(蕴含) | 说话算数的老板:承诺 “完成项目(P)就发奖金(Q)”,只有 “完成项目却没发奖金(P 真 Q 假)” 时,才是骗子 | 真推假假,其余皆真 (仅 P=1、Q=0 时,P→Q=0) | 别纠结 “P 和 Q 没关系” 的情况(比如 “如果 2 是偶数,则太阳从东方升起”),逻辑中只要不是 “真推假”,就为真 |
| ↔ | 当且仅当(等价) | 两端等重的天平:左边(P)和右边(Q)重量一样(真值相同),天平才平衡;不一样就倾斜 | 同真同假,一真一假则假 (P=Q 时,P↔Q=1;P≠Q 时,P↔Q=0) | 可以理解为 “双向蕴含”:既 P→Q,又 Q→P |
三.合式公式的类型与真值函数
1.真值表:命题逻辑的 “真值计算器” 与 “验证工具”
在命题逻辑中,真值表是一种直观、系统的表格工具,用于枚举所有原子命题的真值组合,并计算对应复合命题的真值。它就像逻辑世界的 “计算器”—— 能清晰呈现命题在不同条件下的 “真 / 假” 结果,也是验证公式等值、判断命题类型(永真 / 永假 / 可满足)的核心手段。
(1).真值表的核心构成:3 个关键部分
一张完整的真值表由 “原子命题列”“真值组合列”“复合命题真值列” 三部分组成,以含 2 个原子命题(P、Q)的复合命题(如 P→Q)为例,结构如下:
| 1. 原子命题列(输入) | 2. 真值组合列(所有可能情况) | 3. 复合命题真值列(输出) |
|---|---|---|
| P | Q | P→Q |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
原子命题列:列出复合命题中所有互不相同的简单命题(原子命题),如 P、Q、R 等,是真值表的 “输入变量”。
真值组合列:枚举所有原子命题的真值组合 —— 若有 n 个原子命题,根据 “每个命题有 2 种真值(1 真 / 0 假)”,总组合数为2ⁿ(如 1 个原子命题有 2 种,2 个有 4 种,3 个有 8 种),且组合需按 “二进制递增” 顺序排列(确保不重复、不遗漏)。
复合命题真值列:根据逻辑联结词的定义(如→的 “真推假假,其余皆真”),计算每种真值组合下复合命题的最终真值,是真值表的 “输出结果”。
(2).真值表的制作步骤:4 步标准化流程
以复合命题 “¬(P∧Q)∨(¬P∨¬Q)”(验证德摩根律)为例,标准化制作步骤如下:
步骤 1:确定原子命题与组合数
复合命题中含 2 个原子命题(P、Q),因此真值组合数为 2²=4 种,先列出原子命题列(P、Q)和 4 种真值组合(按 P 从 1 到 0、Q 从 1 到 0 的顺序排列):
| P | Q |
|---|---|
| 1 | 1 |
| 1 | 0 |
| 0 | 1 |
| 0 | 0 |
步骤 2:拆解复合命题为 “子命题”
将复杂命题拆分为易计算的子命题,按 “从内层到外层” 的顺序添加列:
原命题 “¬(P∧Q)∨(¬P∨¬Q)” 可拆解为:
- 子命题 1:P∧Q(内层合取)
- 子命题 2:¬(P∧Q)(子命题 1 的否定)
- 子命题 3:¬P(P 的否定)、¬Q(Q 的否定)
- 子命题 4:¬P∨¬Q(子命题 3 的析取)
添加子命题列后,表格扩展为:
| P | Q | P∧Q | ¬(P∧Q) | ¬P | ¬Q | ¬P∨¬Q |
|---|---|---|---|---|---|---|
| 1 | 1 | |||||
| 1 | 0 | |||||
| 0 | 1 | |||||
| 0 | 0 |
步骤 3:计算各子命题的真值
根据逻辑联结词的规则,逐行计算每个子命题的真值(如 P∧Q “同真才真”,¬P “真假互换”):
| P | Q | P∧Q | ¬(P∧Q) | ¬P | ¬Q | ¬P∨¬Q |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
步骤 4:计算最终复合命题的真值
根据最外层联结词(此处为∨,“有真就真”),结合子命题 2(¬(P∧Q))和子命题 4(¬P∨¬Q)的真值,计算最终结果:
| P | Q | P∧Q | ¬(P∧Q) | ¬P | ¬Q | ¬P∨¬Q | ¬(P∧Q)∨(¬P∨¬Q) |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0∨0=0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1∨1=1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1∨1=1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1∨1=1 |
(3).真值表的核心用途:3 个关键场景
真值表不仅是 “计算工具”,更是命题逻辑的 “验证利器”,核心用途包括:
1. 验证公式等值:判断两个命题是否 “永远同真同假”
若两个复合命题在所有真值组合下的真值完全一致,则它们等值。
例如前文表格中,子命题 2(¬(P∧Q))与子命题 4(¬P∨¬Q)的真值列完全相同(1,1,1,0),可直接验证德摩根律 ¬(P∧Q)⇔¬P∨¬Q成立。
2. 判断命题类型:区分永真式、永假式、可满足式
- 永真式(重言式):所有真值组合下结果均为 1(永远为真),如 P∨¬P(真值表中全为 1)。
- 永假式(矛盾式):所有真值组合下结果均为 0(永远为假),如 P∧¬P(真值表中全为 0)。
- 可满足式:至少存在一种真值组合使结果为 1(有时为真),如 P→Q(前文表格中 3 个 1、1 个 0)。
3. 分析逻辑推理有效性:判断 “前提→结论” 是否为永真式
逻辑推理的有效性等价于 “所有前提的合取→结论” 是永真式。
例如推理 “前提:P→Q,P;结论:Q”,只需验证 “(P→Q)∧P→Q” 的真值表是否全为 1—— 计算后发现所有组合下结果均为 1,因此推理有效。
(4).注意事项:避免出错的 2 个关键点
真值组合不重复、不遗漏:n 个原子命题需列出 2ⁿ种组合,且按 “二进制顺序” 排列(如 3 个原子命题 P、Q、R,按 P 从 1 到 0、Q 从 1 到 0、R 从 1 到 0 的顺序,确保覆盖所有情况)。
子命题计算从内层到外层:复杂命题需先算内层联结词(如括号内的 P∧Q),再算外层联结词(如 ¬(P∧Q)),避免直接计算外层导致逻辑混乱。
总之,真值表是命题逻辑的 “基础工具”—— 无论是理解联结词定义、验证公式等值,还是判断推理有效性,都能通过它直观呈现逻辑规律,尤其适合初学者建立对 “逻辑真值” 的直观认知。
2.合式公式的三种类型
根据真值表中 “最终公式的真值分布”,可将合式公式分为三类:
重言式(永真式):永远为真的公式
无论原子命题取何真值,公式的真值始终为 T。
示例:“p∨¬p”(排中律)、“p→(p∨q)”(上文示例)。
验证 “p∨¬p”:p 为 T 时,¬p 为 F,p∨¬p 为 T;p 为 F 时,¬p 为 T,p∨¬p 为 T—— 所有情况均为 T,是重言式。
矛盾式(永假式):永远为假的公式
无论原子命题取何真值,公式的真值始终为 F。
示例:“p∧¬p”(矛盾律)。
验证 “p∧¬p”:p 为 T 时,¬p 为 F,p∧¬p 为 F;p 为 F 时,¬p 为 T,p∧¬p 为 F—— 所有情况均为 F,是矛盾式。
可满足式:至少存在一种真值组合使公式为真
既不是重言式也不是矛盾式,存在至少一组原子命题真值让公式为 T。
示例:“p∧q”“p→q”。
验证 “p∧q”:当 p=T、q=T 时,公式为 T;当 p=T、q=F 时,公式为 F—— 存在为真的情况,是可满足式。
三者关系:
- 重言式一定是可满足式(因为所有情况都为真,必然存在至少一种);
- 矛盾式一定不是可满足式(所有情况都为假,无任何为真的情况);
- 可满足式包含重言式和 “非重言非矛盾的公式”。
3.真值函数:公式与真值的对应关系
每一个合式公式,本质上都对应一个 “真值函数”—— 以原子命题的真值组合为输入,以公式的真值为输出的函数。若公式含 n 个原子命题,则对应一个 n 元真值函数,记为 F: {T,F}ⁿ → {T,F}。
真值函数的个数:
n 个原子命题有 2ⁿ种输入组合,每种组合的输出有 T、F 两种可能,因此 n 元真值函数共有 2^(2ⁿ) 个。
- 示例:n=1(1 个原子命题 p)时,真值函数有 2^(2¹)=4 个:
- F₁(p)=T(无论 p 取何值,输出均为 T,对应重言式 “p∨¬p”);
- F₂(p)=p(输出与 p 一致,对应公式 “p”);
- F₃(p)=¬p(输出与 p 相反,对应公式 “¬p”);
- F₄(p)=F(无论 p 取何值,输出均为 F,对应矛盾式 “p∧¬p”)。
公式与真值函数的关系:
不同的公式可能对应同一个真值函数(即 “等值公式”)。例如 “¬p∨q” 和 “p→q”,它们的真值表完全一致,对应同一个 2 元真值函数。这也是后续 “等值演算” 的核心基础 —— 通过变形,将复杂公式转化为简单的等值公式,简化逻辑推理。
例题 2:真值表应用(判断公式类型 + 验证等值)
题目要求
(1)用真值表判断公式 (p→q) ∧ p → q 的类型(永真式 / 永假式 / 可满足式);
(2)用真值表验证 德摩根律:¬(p ∨ q) ⇔ ¬p ∧ ¬q。解题步骤(1):判断公式类型
确定原子命题与真值组合:公式含 2 个原子命题(p、q),共 2²=4 种真值组合,按 “p 从 1 到 0,q 从 1 到 0” 排列:
p q 1 1 1 0 0 1 0 0 拆解子命题,逐行计算真值(联结词优先级:¬ > ∧ > →):
- 子命题 1:p→q(按 “真推假假,其余皆真” 计算);
- 子命题 2:(p→q) ∧ p(按 “同真才真” 计算);
- 最终公式:(p→q) ∧ p → q(按 “真推假假” 计算)。
完整真值表:
p q p→q (p→q)∧p (p→q)∧p → q 1 1 1 1∧1=1 1→1=1 1 0 0 0∧1=0 0→0=1 0 1 1 1∧0=0 0→1=1 0 0 1 1∧0=0 0→0=1 判断类型:所有真值组合下最终公式均为 1,因此是 永真式(这也是逻辑推理中的 “假言推理规则”,验证了推理的有效性)。
解题步骤(2):验证德摩根律
1.列出原子命题与真值组合(同(1)的 4 种组合);
2.计算左右两边公式的真值:
左边:¬(p ∨ q)(先算 p∨q,再取否定);
右边:¬p ∧ ¬q(先算 ¬p、¬q,再算合取)。
真值表:
p q p∨q ¬(p∨q)(左边) ¬p ¬q ¬p∧¬q(右边) 1 1 1 0 0 0 0 1 0 1 0 0 1 0 0 1 1 0 1 0 0 0 0 0 1 1 1 1 3.验证等值:左右两边的真值列完全一致(均为 “0,0,0,1”),因此 ¬(p ∨ q) ⇔ ¬p ∧ ¬q 成立。
思路提炼
真值表解题的关键是 “分步计算,不跳步骤”:
① 先列原子命题的所有组合(n 个原子命题列 2ⁿ行,按二进制顺序排列,避免遗漏);
② 子命题计算按 “内层到外层、优先级从高到低”(¬ > ∧/∨ > → > ↔);
③ 判断公式类型:全 1 为永真式,全 0 为永假式,有 1 有 0 为可满足式;验证等值:左右两边真值列完全相同。
四.逻辑等值公式:形象绑定,告别死记硬背
核心公式不用孤立记,而是把它和上面的 “形象锚点” 绑定 —— 公式就是 “角色的行为逻辑”,理解后自然就能推导出来。
1. 双重否定律
E₁:¬¬P ⇔ P
形象绑定:对应 “非(¬)” 的 “开关形象”—— 连着按两下开关(先 ¬P,再 ¬(¬P)),灯的状态和最开始完全一样(比如初始亮→按 1 下灭→按 2 下亮,回到初始)。
口诀:负负得正,双重否定等于肯定。
应用场景:化简公式时去掉多余的否定词,比如把 ¬¬(P→Q) 直接变成 P→Q。
2.等幂律:“重复运算” 的简化规则
这类公式解决 “同一命题重复用∨或∧连接” 的简化问题,核心是 “重复运算不改变结果”。
E₂:P∨P ⇔ P
逻辑含义:“P 或 P” 的结果仍为 P(同一命题重复析取,等价于原命题)。
通俗理解:“我去吃饭,或我去吃饭”=“我去吃饭”,重复表述不改变原意。
应用场景:化简公式中重复的析取项,例如 (P∨Q)∨P ⇔ P∨Q(先通过交换律将 P 移到前面,再用幂等律消去重复的 P)。
E₃:P∧P ⇔ P
逻辑含义:“P 且 P” 的结果仍为 P(同一命题重复合取,等价于原命题)。
通俗理解:“我写作业,且我写作业”=“我写作业”,重复条件不改变事实。
应用场景:化简公式中重复的合取项,例如 (P∧¬Q)∧P ⇔ P∧¬Q(直接消去重复的 P)。
3.交换律
E₄:P∨Q ⇔ Q∨P
逻辑含义:“P 或 Q” 与 “Q 或 P” 等价(析取运算的左右项顺序不影响真值)。
示例:“今天下雨,或今天刮风”=“今天刮风,或今天下雨”,两种表述的逻辑意义完全一致。
应用场景:调整公式中析取项的顺序,方便后续用结合律或分配律化简,例如 (P∨Q)∧R ⇔ (Q∨P)∧R(先交换 P 和 Q 的顺序,再观察是否能提取公因子)。
E₅:P∧Q ⇔ Q∧P
逻辑含义:“P 且 Q” 与 “Q 且 P” 等价(合取运算的左右项顺序不影响真值)。
示例:“小明爱学习,且小明爱运动”=“小明爱运动,且小明爱学习”,两种表述的事实不变。
应用场景:调整公式中合取项的顺序,例如 (P∧Q)∨(R∧P) ⇔ (Q∧P)∨(P∧R)(交换后可提取公因子 P,用分配律化简)。
4.结合律
这类公式对应 “加法结合律((a+b)+c=a+(b+c))”“乘法结合律((a×b)×c=a×(b×c))”,核心是 “∨和∧的分组括号可移动”。
E₆:(P∨Q)∨R ⇔ P∨(Q∨R)
逻辑含义:先将 P 和 Q 析取,再与 R 析取;等价于先将 Q 和 R 析取,再与 P 析取(析取的分组方式不影响结果)。
示例:“(吃苹果或吃香蕉)或吃橙子”=“吃苹果或(吃香蕉或吃橙子)”,最终都是 “三种水果选至少一种”。
应用场景:重组析取项的分组,方便合并同类项,例如 (P∨¬P)∨Q ⇔ P∨(¬P∨Q)(先计算 P∨¬P=1,再用同一律化简为 1∨Q=1)。
E₇:(P∧Q)∧R ⇔ P∧(Q∧R)
逻辑含义:先将 P 和 Q 合取,再与 R 合取;等价于先将 Q 和 R 合取,再与 P 合取(合取的分组方式不影响结果)。
示例:“(写数学作业且写语文作业)且写英语作业”=“写数学作业且(写语文作业且写英语作业)”,最终都是 “三种作业都写”。
应用场景:重组合取项的分组,例如 (P∧1)∧Q ⇔ P∧(1∧Q)(先计算 1∧Q=Q,再用同一律化简为 P∧Q)。
5.分配律
E₈:P∧(Q∨R) ⇔ (P∧Q)∨(P∧R)
逻辑含义:P 与 “Q 或 R” 的合取,等价于 “P 与 Q 的合取” 或 “P 与 R 的合取”(将∧分配到∨的每一项上)。
示例:“我买了(苹果或香蕉)”=“我买了苹果,或我买了香蕉”,两种表述都表示 “买的水果是苹果 / 香蕉中的一种”。
应用场景:将 “合取 + 析取” 的嵌套公式展开,方便化简,例如 P∧(¬P∨Q) ⇔ (P∧¬P)∨(P∧Q)(展开后 P∧¬P=0,最终简化为 0∨(P∧Q)=P∧Q)。
E₉:P∨(Q∧R) ⇔ (P∨Q)∧(P∨R)
逻辑含义:P 与 “Q 且 R” 的析取,等价于 “P 与 Q 的析取” 且 “P 与 R 的析取”(将∨分配到∧的每一项上)。
示例:“我吃了饭,或(我吃了面且喝了汤)”=“(我吃了饭或吃了面)且(我吃了饭或喝了汤)”,两种表述的逻辑真值完全一致(可通过真值表验证)。
应用场景:将 “析取 + 合取” 的嵌套公式展开,例如 ¬P∨(P∧Q) ⇔ (¬P∨P)∧(¬P∨Q)(展开后 ¬P∨P=1,最终简化为 1∧(¬P∨Q)=¬P∨Q)。
6. 德摩根律
德摩根律是化简 “否定合取 / 否定析取” 的关键,记住 “老板否定门卫 / 朋友” 的场景,就永远不会错。
E₁₀:¬(P ∨ Q) ⇔ ¬P ∧ ¬Q
形象绑定:“或(∨)” 是大度朋友,说 “P 来或 Q 来都可以”;现在 “非(¬)” 这个老板来否定这件事,老板说 “不行!”—— 意思是 “P 不能来(¬P),并且(∧)Q 也不能来(¬Q)”,只有两个人都不来,才能否定 “有人来” 的原说法。
应用场景:化简 “否定析取” 类公式,例如 ¬(¬P∨Q) ⇔ P∧¬Q(拆括号分否定词,∨变∧)。
口诀:否定 “或”,变 “且”,否定词分到每一项。
E₁₁:¬(P ∧ Q) ⇔ ¬P ∨ ¬Q
形象绑定:“且(∧)” 是严格门卫,说 “P 有票且 Q 有票才能进”;老板(¬)否定这个规矩,说 “不用这么严!”—— 意思是 “P 没票(¬P)也行,或者(∨)Q 没票(¬Q)也行”,只要有一个人没票,原规矩就不成立。
口诀:否定 “且”,变 “或”,否定词分到每一项。
德摩根律综合口诀:拆括号,分负号,且变或,或变且。
应用场景:化简带否定的复合公式,比如 ¬(¬P ∧ Q) ⇔ P ∨ ¬Q(拆括号分负号,∧变∨)。
7.吸收律
E₁₂:P∨(P∧Q) ⇔ P
逻辑含义:“P 或(P 且 Q)” 等价于 P(因为 “P 且 Q” 是 “P 成立” 的子集 —— 若 P 且 Q 为真,则 P 必为真,所以析取后结果就是 P)。
形象记忆:“我去玩,或(我去玩且带朋友)”=“我去玩”,“带朋友” 是 “去玩” 的附加条件,不影响 “去玩” 的核心事实。
应用场景:消去公式中 “被包含” 的合取项,例如 (P∨Q)∨((P∨Q)∧R) ⇔ P∨Q(将 “P∨Q” 视为整体,直接用吸收律消去后面的合取项)。
E₁₃:P∧(P∨Q) ⇔ P
逻辑含义:“P 且(P 或 Q)” 等价于 P(因为 “P 或 Q” 是 “P 成立” 的超集 —— 若 P 为真,则 “P 或 Q” 必为真,所以合取后结果就是 P)。
形象记忆:“我在家,且(我在家或出门)”=“我在家”,“出门” 是 “在家” 的对立选项,但 “在家” 为真时,“在家或出门” 必为真,合取后仍为 “在家”。
应用场景:消去公式中 “包含” 的析取项,例如 (P∧¬Q)∧((P∧¬Q)∨R) ⇔ P∧¬Q(将 “P∧¬Q” 视为整体,用吸收律消去后面的析取项)。
8.零律与9.同一律
这类公式涉及 “永真命题(用 1 表示,所有真值组合都为真)” 和 “永假命题(用 0 表示,所有真值组合都为假)”,是公式化简的 “终点工具”。
E₁₄:P∨1 ⇔ 1
逻辑含义:“P 或永真命题” 等价于永真命题(因为永真命题本身已为真,析取任何命题后仍为真)。
示例:“今天下雨,或 1+1=2”=“1+1=2”(1+1=2 是永真命题,所以整体为真)。
应用场景:公式化简的 “终点” 之一,例如 (P∧Q)∨1 ⇔ 1(无论 P∧Q 是真还是假,与 1 析取后都是 1)。
E₁₅:P∧0 ⇔ 0
逻辑含义:“P 且永假命题” 等价于永假命题(因为永假命题本身已为假,合取任何命题后仍为假)。
示例:“今天晴天,且 1+1=3”=“1+1=3”(1+1=3 是永假命题,所以整体为假)。
应用场景:公式化简的 “终点” 之一,例如 (P∨Q)∧0 ⇔ 0(无论 P∨Q 是真还是假,与 0 合取后都是 0)。
E₁₆:P∨0 ⇔ P
逻辑含义:“P 或永假命题” 等价于 P(因为永假命题为假,析取后结果由 P 的真值决定)。
示例:“我看书,或 1+1=3”=“我看书”(1+1=3 为假,不影响 “我看书” 的真值)。
应用场景:消去公式中的永假项,例如 (P∧¬Q)∨0 ⇔ P∧¬Q(直接去掉 0,保留核心项)。
E₁₇:P∧1 ⇔ P
逻辑含义:“P 且永真命题” 等价于 P(因为永真命题为真,合取后结果由 P 的真值决定)。
示例:“我写字,且 1+1=2”=“我写字”(1+1=2 为真,不影响 “我写字” 的真值)。
应用场景:消去公式中的永真项,例如 (P∨Q)∧1 ⇔ P∨Q(直接去掉 1,保留核心项)。
10.否定律
E₁₈:P∨¬P ⇔ 1
逻辑含义:“P 或非 P” 等价于永真命题(矛盾命题必有一真,析取后恒为真,也叫 “排中律”)。
示例:“今天下雨,或今天不下雨”—— 无论天气如何,这句话永远为真,不存在第三种可能。
应用场景:化简公式中的 “矛盾命题析取” 项,例如 (P∨¬P)∧Q ⇔ 1∧Q ⇔ Q(先通过互补律将 P∨¬P 化为 1,再用同一律化简)。
E₁₉:P∧¬P ⇔ 0
逻辑含义:“P 且非 P” 等价于永假命题(矛盾命题不可能同时为真,合取后恒为假,也叫 “矛盾律”)。
示例:“今天下雨,且今天不下雨”—— 这句话永远为假,不可能同时发生。
应用场景:化简公式中的 “矛盾命题合取” 项,例如 (P∧¬P)∨Q ⇔ 0∨Q ⇔ Q(先通过互补律将 P∧¬P 化为 0,再用同一律化简)。
11. 蕴含等值式
E₂₀:P → Q ⇔ ¬P ∨ Q
形象绑定:对应 “蕴含(→)” 的 “老板形象”—— 老板承诺 “P(完成项目)则 Q(发奖金)”,什么时候老板不算骗子?两种情况:
1.你没完成项目(¬P 为真):不管发不发奖金,老板都没违约;
2.你完成项目且老板发了奖金(Q 为真):老板守诺。
这两种情况用 “或(∨)” 连接,就是 “¬P ∨ Q”,和原蕴含式完全等价。
口诀:“推” 变 “或非”,看见→,就把前件否定、后件保留,中间变∨。
应用场景:把蕴含式转化为 “否定 + 析取”,方便后续化简或证明,比如证明 P→Q 和 ¬P∨Q 等值,直接用这个公式一步转换。
12.等价等值式
E₂₁:P↔Q ⇔ (P→Q)∧(Q→P)
13. 逆否律
E₂₂:P → Q ⇔ ¬Q → ¬P
形象绑定:还是 “老板承诺” 的场景 —— 老板说 “完成项目(P)则发奖金(Q)”(P→Q),等价于另一句话:“如果没发奖金(¬Q),那你肯定没完成项目(¬P)”(¬Q→¬P)。这是典型的 “抓骗子逻辑”:如果老板没发奖金,还说你完成了项目,那他就是骗子;所以要证明老板没骗你,只要证明 “没发奖金→没完成项目” 就行。
口诀:原命题等价于逆否命题,前件后件互换,同时加否定。
应用场景:当直接证明 P→Q 困难时,转而去证明 ¬Q→¬P(逆否命题),比如证明 “如果 n² 是偶数,则 n 是偶数”,等价于证明 “如果 n 不是偶数,则 n² 不是偶数”,后者更易证。
14.输出律
E₂₃:(P ∧ Q → R) ⇔ (P → (Q → R))
逻辑含义:如果 “P 且 Q 能推出 R”,等价于 “若 P 成立,则 Q 能推出 R”。
可以理解为:当两个条件 P 和 Q 共同导致结果 R 时,可将其中一个条件 P 作为前提,另一个条件 Q 作为蕴含的前件,即 “如果 P 已满足,那么只要 Q 成立就能推出 R”。
形象记忆:假设 “(努力学习(P)且方法正确(Q))→ 考试及格(R)”,这句话等价于 “如果努力学习(P),那么(只要方法正确(Q)→ 考试及格(R))”。
即:将两个并列条件中的一个 “输出” 为前提,另一个保留为蕴含关系的前件,逻辑意义不变。
应用场景:常用于公式的 “拆分” 或 “嵌套” 转换,例如:
化简 (A ∧ B ∧ C → D) 时,可通过输出律逐步拆分:
→ A → (B ∧ C → D)
→ A → (B → (C → D))
使公式的层次更清晰,便于后续推理或证明。
15.归谬论
E₂₄:(P→Q)∧(P→¬Q) ⇔ ¬P
逻辑含义:“如果 P 则 Q,且如果 P 则非 Q” 等价于 “非 P”(若一个前提 P 能推出两个矛盾的结论 Q 和 ¬Q,说明前提 P 本身必为假)。
形象记忆:“如果他是好人(P),则他会救人(Q);且如果他是好人(P),则他不会救人(¬Q)”—— 这两个结论矛盾,说明 “他是好人(P)” 必为假,即 “他不是好人(¬P)”。
应用场景:间接证明 “¬P”,只需证明 “P 能推出矛盾结论”,例如证明 “‘2 是奇数(P)’为假”,可证明 “若 2 是奇数(P),则 2 不能被 2 整除(Q);且若 2 是奇数(P),则 2 能被 2 整除(¬Q)”,通过归谬论得出 ¬P(2 不是奇数)。
总结:24 条公式的 “记忆优先级与关联逻辑”
为避免混淆,可按 “核心工具→基础规律→特殊场景” 的优先级记忆,同时注意公式间的推导关系:
| 记忆优先级 | 公式类别 | 关键作用 | 关联逻辑 |
|---|---|---|---|
| 最高 | 德摩根律、蕴含等值式 | 拆否定、消→(所有复杂公式化简的起点) | 德摩根律是否定运算的核心,蕴含等值式是连接→与 ¬/∨的桥梁 |
| 高 | 交换律、结合律、分配律 | 调整公式结构(展开、重组项) | 类似数学中的加减乘除规律,是公式 “变形” 的基础 |
| 中 | 双重否定律、幂等律、吸收律、输出律 | 简化冗余项(消重复、消包含项) | 基于 “否定两次为肯定”“重复运算不变”“包含项可消” 的直觉 |
| 中 | 零律、同一律、互补律 | 化简至 “终点”(得到 1 或 0) | 互补律是基础,零律 / 同一律依赖互补律推导(如 P∨1=1 可由 P∨(P∨¬P)=P∨¬P=1 推导) |
| 低 | 等价相关公式、归谬论 | 处理双向逻辑与矛盾证明 | 等价式依赖蕴含式,归谬论是蕴含式的特殊矛盾场景应用 |
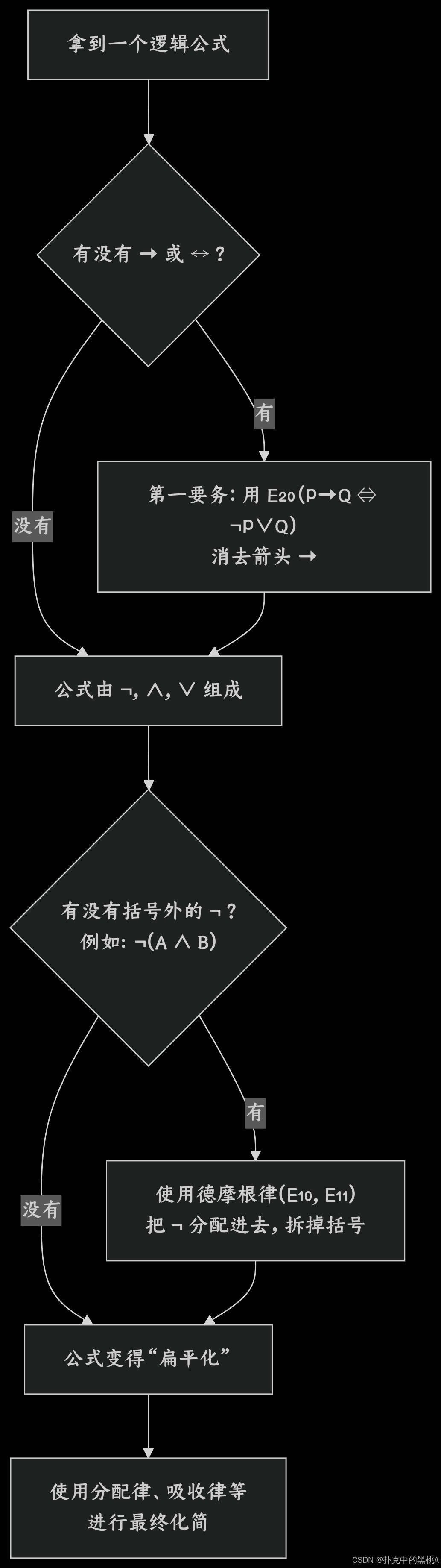
解题流程图解析
1.拿到逻辑公式:如 ¬(A ∧ B)、(P→Q)∨R 等,作为处理起点。
2.消去蕴含(→)或等价(↔):若公式含 → 或 ↔,优先用 蕴含等值式(P→Q ⇔ ¬P∨Q) 消去 →(↔ 可拆为双向 →,再分步消去),让公式仅含 ¬、∧、∨。
示例:化简 (P→Q)∧¬R → 用 E₂₀ 转化为 (¬P∨Q)∧¬R。
3.处理括号外的否定(¬):若公式有括号外的 ¬(如 ¬(A∧B)、¬(C∨D) ),用 德摩根律 拆括号、变联结词,将 ¬ 分配到单个命题上。
示例:化简 ¬(¬P∨Q) → 用德摩根律转化为 P∧¬Q。
4.公式 “扁平化” 后,用分配律、吸收律等化简:经过前两步,公式只剩 ¬、∧、∨,可继续用分配律(A∧(B∨C)⇔(A∧B)∨(A∧C) 等)、吸收律(A∨(A∧B)⇔A 等)进一步化简,直到最简形式。
示例:化简 (P∧¬Q)∨(P∧R) → 用分配律提取 P,得到 P∧(¬Q∨R)。
5.终极验证:真值表:若不确定化简结果是否正确,列出所有原子命题的真值组合,分别计算原公式和化简后公式的真值,若每一行真值一致,则化简正确。
例题 3:公式化简(用 24 条等值公式化简复杂公式)
题目要求
用核心等值公式化简下列公式,最终结果仅含 “¬、∧、∨”,且否定词仅作用于原子命题:
(1)¬(p ∧ ¬q) ∨ ¬r;
(2)(p→q) ∧ ¬q → ¬p。解题步骤(1):化简 ¬(p ∧ ¬q) ∨ ¬r
1.用德摩根律拆否定(优先处理括号外的 ¬):
¬(p ∧ ¬q) ⇔ ¬p ∨ q(德摩根律:¬(A∧B)⇔¬A∨¬B,此处 B=¬q,故 ¬B=q);2.代入原公式,整理结果:
原公式 ⇔ (¬p ∨ q) ∨ ¬r ⇔ ¬p ∨ q ∨ ¬r(结合律:(A∨B)∨C⇔A∨(B∨C),可去掉括号);3.最终化简结果:¬p ∨ ¬r ∨ q(交换律:A∨B⇔B∨A,顺序可调整,不影响真值)。
解题步骤(2):化简 (p→q) ∧ ¬q → ¬p
1.用蕴含等值式消去→(优先消去蕴含词):
- 先处理前件:p→q ⇔ ¬p ∨ q(蕴含等值式:A→B⇔¬A∨B);
- 原公式是 “(前件) → ¬p”,再次用蕴含等值式:(A→B)⇔¬A∨B,其中 A=(p→q)∧¬q,B=¬p;
- 因此原公式 ⇔ ¬[(¬p ∨ q) ∧ ¬q] ∨ ¬p;
2.用德摩根律拆否定:
¬[(¬p ∨ q) ∧ ¬q] ⇔ ¬(¬p ∨ q) ∨ ¬(¬q)(德摩根律:¬(A∧B)⇔¬A∨¬B);
进一步化简:¬(¬p ∨ q) ⇔ p ∧ ¬q(德摩根律),¬(¬q) ⇔ q(双重否定律);
因此前半部分 ⇔ (p ∧ ¬q) ∨ q;3.用分配律展开并化简:
(p ∧ ¬q) ∨ q ⇔ (p ∨ q) ∧ (¬q ∨ q)(分配律:A∨(B∧C)⇔(A∨B)∧(A∨C),此处 A=q,B=p,C=¬q);
其中 ¬q ∨ q ⇔ 1(互补律:A∨¬A⇔1),因此 ⇔ (p ∨ q) ∧ 1;4.用同一律化简:
(p ∨ q) ∧ 1 ⇔ p ∨ q(同一律:A∧1⇔A);5.代入原公式,最终化简:
原公式 ⇔ (p ∨ q) ∨ ¬p ⇔ (p ∨ ¬p) ∨ q ⇔ 1 ∨ q ⇔ 1(互补律:p∨¬p⇔1;零律:1∨A⇔1);
最终化简结果:1(永真式)。思路提炼
公式化简的 “黄金流程”:
① 第一步:消去→和↔(用蕴含等值式 A→B⇔¬A∨B,等价等值式 A↔B⇔(A→B)∧(B→A));
② 第二步:拆否定(用德摩根律将 ¬ 分配到原子命题上,消除 “¬(A∧B)”“¬(A∨B)” 形式);
③ 第三步:化简(用分配律、吸收律、互补律、零律 / 同一律等消去冗余项,如 A∧A⇔A、A∨(A∧B)⇔A、A∧¬A⇔0);
④ 目标:最终结果仅含原子命题、¬、∧、∨,且无重复项、无冗余括号。
例题 4:推理有效性验证(用真值表 + 等值演算两种方法)
题目要求
验证推理:“如果今天下雨(p),则路滑(q);今天下雨了(p);因此路滑(q)” 的有效性(即判断 “(p→q) ∧ p → q” 是否为永真式)。
方法 1:真值表法(同例题 2(1))
- 已通过真值表计算得出,“(p→q) ∧ p → q” 的所有真值均为 1,是永真式,因此推理 有效。
方法 2:等值演算法(用 24 条公式推导)
1.将推理转化为公式:推理的有效性等价于 “(前提 1 ∧ 前提 2)→ 结论”,即 (p→q) ∧ p → q;
2.用等值公式推导:
- 第一步:消去→:(p→q) ∧ p → q ⇔ ¬[(p→q) ∧ p] ∨ q(蕴含等值式:A→B⇔¬A∨B);
- 第二步:拆否定:¬[(p→q) ∧ p] ∨ q ⇔ ¬(p→q) ∨ ¬p ∨ q(德摩根律:¬(A∧B)⇔¬A∨¬B);
- 第三步:消去 p→q:¬(¬p ∨ q) ∨ ¬p ∨ q(蕴含等值式:p→q⇔¬p∨q);
- 第四步:拆否定:(p ∧ ¬q) ∨ ¬p ∨ q(德摩根律:¬(¬p∨q)⇔p∧¬q);
- 第五步:重组并化简:
(p ∧ ¬q) ∨ (¬p ∨ q) ⇔ (p ∧ ¬q) ∨ ¬(p ∧ ¬q)(德摩根律:¬p∨q⇔¬(p∧¬q));
令 A = p ∧ ¬q,则公式 ⇔ A ∨ ¬A ⇔ 1(互补律:A∨¬A⇔1);3.结论:推导结果为永真式(1),因此推理 有效。
思路提炼
- 推理有效性验证的核心逻辑:
① 推理 “前提 1,前提 2,…,前提 n → 结论” 有效,当且仅当公式 “(前提 1 ∧ 前提 2 ∧ … ∧ 前提 n) → 结论” 是永真式;
② 验证方法二选一:
- 真值表法:列出所有组合,判断公式是否全为 1;
- 等值演算法:通过等值公式推导,若最终结果为 1(永真式),则推理有效。
五.全功能联结词:逻辑武器的 “最小套装”
核心思想:用最少的 “零件” 拼出所有逻辑公式
想象你要组装一台 “逻辑公式制造机”,需要买 “逻辑零件”(联结词)。问题来了:最少买哪几个零件,就能拼出任何逻辑公式?
这组 “最少且够用” 的零件,就是极小全功能联结词集合。理解它,你就能明白 “为什么计算机只用一种门电路(如与非门)就能实现所有运算”,数学和现实的关联瞬间打通!
1. 经典 “精简套装”:3 组常用组合
{¬, ∧}(非 + 且):用 “且” 和 “非” 拼出 “或”
(1).想拼出 “P∨Q”(P 或 Q),利用德摩根律:
P ∨ Q ⇔ ¬(¬P ∧ ¬Q)
记忆场景:电影院门卫(∧)说 “必须 P 和 Q 都有票才能进”,现在 “非(¬)” 否定这个规矩,等价于 “不是(¬P 且 ¬Q)”—— 只要不是两人都没票,就至少有一人有票(P 或 Q 成立)。
(2).{¬, ∨}(非 + 或):用 “或” 和 “非” 拼出 “且”
想拼出 “P∧Q”(P 且 Q),同样用德摩根律:
P ∧ Q ⇔ ¬(¬P ∨ ¬Q)
记忆场景:朋友(∨)说 “P 或 Q 来一个就行”,现在 “非(¬)” 否定这个宽松规矩,等价于 “不是(¬P 或 ¬Q)”—— 不能有一个人没来,必须两人都来(P 且 Q 成立)。
(3).{¬, →}(非 + 蕴含):最接近数学推理的套装
拼 “且”(P∧Q):P ∧ Q ⇔ ¬(P → ¬Q)
理解:“P 且 Q 成立” = “如果 P 成立,那么 Q 不成立(P→¬Q)” 是错的(¬ 否定这个错误说法)。
场景:老板说 “如果完成项目(P),就不发奖金(¬Q)”—— 这显然和 “完成项目且发奖金(P∧Q)” 矛盾,所以否定老板的话,就等价于 P∧Q。
拼 “或”(P∨Q):P ∨ Q ⇔ ¬P → Q(蕴含等值式,前面学过!)
场景:“没完成项目(¬P),就发奖金(Q)” 等价于 “完成项目或发奖金(P∨Q)”,完美对应数学里的 “兜底承诺”。
2. 终极 “一件套装”:只用 1 个联结词,拼出全世界!
如果老板说 “只能卖你 1 种零件”,别慌,有两个 “大神级” 联结词能搞定一切 ——与非(↑)和或非(↓)。
(1).与非(NAND):P ↑ Q ⇔ ¬(P ∧ Q)
定义:“并非两者都真”—— 只有 P、Q都真时,P↑Q 为假;其他情况都为真。
形象记忆:团队里的 “挑刺专家”—— 只要不是所有人都完美(真),他就挑刺(结果为真);所有人都完美时,他没刺可挑(结果为假)。
拼 “非”(¬P):¬P ⇔ P ↑ P(P 和自己与非 = 非 P)
场景:“我和自己都完美” = 不可能,所以结果为假(¬P 为假时 P 为真,反之同理)。
拼 “且”(P∧Q):P ∧ Q ⇔ (P ↑ Q) ↑ (P ↑ Q)
逻辑:先算 P↑Q = ¬(P∧Q)(非且),再对 “非且” 与非一次,得到 ¬(¬(P∧Q)) = P∧Q(双重否定变肯定)。
(2).或非(NOR):P ↓ Q ⇔ ¬(P ∨ Q)
定义:“两者都不真”—— 只有 P、Q都假时,P↓Q 为真;其他情况都为假。
形象记忆:“绝望的悲观主义者”—— 只有所有选项都糟糕(假),他才认同(真);有一个好的(真),他就反对(假)。
拼 “非”(¬P):¬P ⇔ P ↓ P(P 和自己或非 = 非 P)
场景:“我或我自己” = 就是我自己,所以 “都不真” 只有当我自己为假时成立(¬P 为真时 P 为假,反之同理)。
拼 “或”(P∨Q):P ∨ Q ⇔ (P ↓ Q) ↓ (P ↓ Q)
逻辑:先算 P↓Q = ¬(P∨Q)(非或),再对 “非或” 或非一次,得到 ¬(¬(P∨Q)) = P∨Q(双重否定变肯定)。
全功能联结词的意义
理论上,现代计算机只用一种基础门电路(如与非门)就能实现所有计算!因为所有逻辑公式都能拆解为与非(或或非)的组合 —— 这就是数学对现实科技的底层支撑,是不是超酷?
六.对偶原理:逻辑世界的 “镜面反射”
核心思想:逻辑公式的 “阴阳对称”
在只包含 {¬, ∧, ∨} 的公式里,存在一种神奇的对称性—— 很多公式就像 “物体和镜子里的影子”,成对出现。掌握对偶原理,证明公式直接 “买一送一”!
1. 如何制造 “对偶影子”?(操作口诀)
对任意逻辑公式(仅含 ¬、∧、∨、0、1),做 3 步操作:
∧ ↔ ∨(“且” 和 “或” 互换)
0 ↔ 1(“永假” 和 “永真” 互换)
¬ 不动(否定词原地待命)
示例:
原式 A = ¬p ∨ (q ∧ r)
对偶式 A* = ¬p ∧ (q ∨ r)(∨和∧互换,¬p、q、r 不动)
原式 B = (p ∨ q) ∧ 0
对偶式 B* = (p ∧ q) ∨ 1(∨和∧互换,0 和 1 互换,其他不动)
2. 对偶原理的 “买一送一” 魔力
核心定理:如果两个公式等值(A ⇔ B),那么它们的对偶式也等值(A* ⇔ B*)。
为什么厉害?
比如你辛苦证明了分配律:
A ∨ (B ∧ C) ⇔ (A ∨ B) ∧ (A ∨ C)(或对且的分配)
根据对偶原理,直接得到它的 “镜面对称” 公式(且对或的分配):
A ∧ (B ∨ C) ⇔ (A ∧ B) ∨ (A ∧ C)
工作量直接减半!证明一个,另一个自动成立 —— 这就是逻辑世界的 “阴阳平衡”,省力又神奇!
形象记忆
对偶原理就像逻辑界的 “照镜子”—— 公式 A 在镜子里的影子是 A*,如果 A 站得稳(等值成立),那么影子 A * 也一定站得稳。
总结
现在再看离散数学,是不是觉得它不再是枯燥的公式,而是一套能解释现实、指导科技的 “思维工具”?继续往下学,你会发现更多数学和现实的奇妙关联!
