应用密码学课程复习汇总2——古典密码学
隐写术
隐写术(Steganography)是一种将秘密信息隐藏于其他公开载体(如图像、文本、音频等)中的技术。
庐剧《无双缘》中,双写也以藏头诗表明心志:“早妆未罢暗凝眉,迎户愁看紫燕飞,无力回天春已老,双栖画栋不如归。”暗藏“早迎无双”四字。
其他隐写:琴声、显微镜、物理密写、图像隐藏、量子等
优点:
- 隐蔽性强:能够在不引起第三方察觉的情况下实现秘密通信,通信双方的存在和通信行为本身不易暴露。
- 区别于加密:与加密技术相比,隐写术不直接显示“正在进行保密通信”,因此更不易引发审查或监控者的注意。
缺点:
- 效率较低:隐藏信息通常需要较复杂的构造过程,开销较大,能嵌入的信息量相对有限。
- 脆弱性高:一旦隐藏方法被识破,该系统立即失效,所有以往传输的信息都可能被提取或破坏。
- 缺乏稳健性:隐写内容容易因载体修改(如压缩、缩放、转码等)而导致隐藏信息丢失或损坏。
代替
凯撒密码(Caesar Cipher)是一种诞生于公元前1世纪的古典替换密码,其加密方式是将明文中的每个字母在字母表中向后(或向前)移动固定数量的位置(该数量称为密钥),以生成密文。
示例:
- 明文:fourscoreandsevenyearsago
- 密钥:3(即每个字母向后移动3位)
- 加密过程:f → Io → Ru → Xr → U...(依此类推)
- 密文结果:IRXUVFRUHDAGVHYHABHDUVDIR
明文中的字母由其他字母、数字或符号所取代的一种方法,具体的代替方案称之为密钥
凯撒密码的问题是密钥空间过小
凯撒密码的密钥空间仅为26(即字母表位移量n∈[1,25]),攻击者通过穷举攻击最多尝试25次即可破解。例如:
- 截获密文:IRXUVFRUHDAGVHYHABHDUVDIR
- 破解过程:仅需测试1~25位位移(平均13次尝试),即可还原明文fourscoreandsevenyearsago。
改进方案:简单替换密码
通过将字母表的任意排列组合作为密钥,可显著提升安全性:
- 密钥空间扩大至26!≈2^88:远超凯撒密码的26种可能,使穷举攻击在计算上不可行。
- 加密方式:每个明文字母被唯一映射为另一个字母(如a→X, b→Z, c→Q,...),形成随机替换表。
单表代替
单表代替密码
单表代替密码(Monoalphabetic Substitution Cipher)通过使用一个密钥词来生成替换字母表,从而实现加密。具体步骤如下:
密钥处理:
- 密钥词:spectacular
- 处理方式:去除重复字母,得到唯一字符序列:spectaulr
- 补充剩余字母:将密钥字唯一序列置于字母表开头,后续按字母顺序补充未出现字母,形成新字母序列:s p e c t a u l r b d f g h i j k m n o q v w x y z
加密对应关系:
- 原始字母序列:a b c d e f g h i j k l m n o p q r s t u v w x y z
- 代替字母序列:s p e c t a u l r b d f g h i j k m n o q v w x y z
加密示例:
- 明文:china
- 加密过程:c → eh → li → rn → ha → s
- 密文结果:elrhs
仿射密码
仿射密码是一种基于线性变换的单表替换加密算法,其加密和解密过程均通过数学公式定义。该密码结合了乘法密码和移位密码(凯撒密码)的特点。
加密过程
加密函数为:
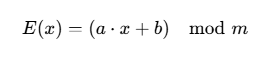
其中:
- x:明文字母在字母表中的位置(通常从 0 开始编号,如 A=0, B=1, ..., Z=25);
- a:乘法密钥,必须与模数 m(通常为 26)互质,即 gcd(a,26)=1;
- b:加法密钥(移位量),取值范围为 0≤b;
- m:字母表大小(通常为 26)。
解密过程
解密函数为:
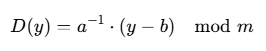
其中:
- y:密文字母的位置;
- a^−1:a在模 m下的乘法逆元,即满足 a⋅a^−1≡1(mod26)的整数;
- b:与加密时使用的加法密钥相同。
示例
假设密钥 a=3, b=5,加密明文 "HELLO"(字母表 A=0, B=1, ..., Z=25):
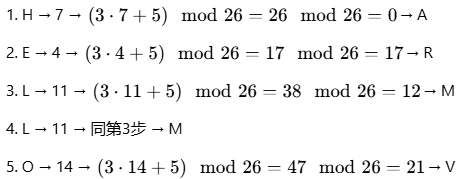
密文为:"ARM MV"(分组后常写作 ARMMV)。
特点与安全性
- 密钥空间有限:仅 a有 12 种可能(与 26 互质的数),b有 26 种可能,总密钥量仅 12×26=312种,易受穷举攻击。
- 安全性低:仍保留单字母频率统计特征,易通过频率分析破解。
- 应用场景:主要用于教学,理解古典密码的基本数学原理。
注意事项
- a必须与 26 互质,否则解密时无法求乘法逆元,导致无法正确解密。
- 需避免弱密钥(如 a=1,b=0时即为恒等变换,无加密效果)。
仿射密码是古典密码学中重要的线性替换密码,为现代密码学中的数学工具(如模运算、逆元)提供了基础示例。
单表代替的缺陷
对简单替换密码的攻击表明,仅依靠大的密钥空间并不能保证密码系统的安全性。密码设计者必须防范各种高效的分析方法(或称“捷径攻击”)。一种典型的频率分析攻击包括以下步骤:
- 统计字母出现频率:对密文中每个字母的出现次数进行统计,计算其频率分布。
- 与标准频率对比并建立假设:将密文字母的频率与自然语言(如英语)的标准字母频率进行对比,据此提出明文字母与密文字母之间的可能对应关系假设。
- 验证或修正假设:基于上下文、常见词汇或字母组合(如双字母、三字母组合)进一步验证假设是否正确;如不成立,则调整或提出新假设,逐步恢复明文。
多表代替
Playfair密码
Playfair密码是一种经典的多表代替加密算法,其核心是使用一个5×5的字母矩阵进行加密和解密。该密码的设计显著提高了对频率分析攻击的抵抗能力。
密钥矩阵的构造方法:
- 使用一个关键词(或密钥短语)作为基础。
- 从左到右、从上到下依次填入关键词中的字母(忽略重复出现的字母)。
- 在关键词填入后,按字母表顺序(A–Z)填入剩余字母,其中 I 和 J 被视为同一个字母,通常以 I 代表两者。
加密特性:
- Playfair密码属于多表代替密码,其加密过程引入了上下文相关性,改变了单表代替中明文字符与密文字符一一对应的关系,从而有效破坏了明文中的统计规律(如字母频率、常见字母组合),增强了对抗频率分析的能力。
例题
密钥是:PLAYFAIR IS A DIGRAM CIPHER。如果明文是:P=playfair cipher。明文两个一组: pl ay fa ir ci ph er
第一步:构建 5x5 密钥矩阵
- 处理密钥:密钥是 “PLAYFAIR IS A DIGRAM CIPHER”。移除空格和非字母字符,得到:PLAYFAIRISADIGRAMCIPHER将字母全部转换为大写(Playfair密码通常不区分大小写):PLAYFAIRISADIGRAMCIPHER去除重复的字母(从左到右,保留首次出现的):P, L, A, Y, F, I, R, S, D, G, M, C, H, E现在,密钥中的唯一字母序列是:P L A Y F I R S D G M C H E
- 填充矩阵:将上述序列按顺序填入5x5的网格中。
- 填入剩余字母:在密钥字母之后,按字母表顺序(A-Z)填入剩余的字母。注意:I 和 J 共享同一个位置。因为我们已经在密钥中使用了 I,所以矩阵中不会再有 J。密钥已用字母:A, C, D, E, F, G, H, I, L, M, P, R, S, Y剩余字母:B, J (忽略,与I合并), K, N, O, Q, T, U, V, W, X, Z按顺序将剩余字母填入矩阵。
最终构建出的密钥矩阵如下:
0 | 1 | 2 | 3 | 4 | |
0 | P | L | A | Y | F |
1 | I | R | S | D | G |
2 | M | C | H | E | B |
3 | K | N | O | Q | T |
4 | U | V | W | X | Z |
这个矩阵是后续所有加密查找的基础。
第二步:准备明文
- 明文:playfair cipher
- 处理明文:转换为大写:PLAYFAIR CIPHER移除空格和非字母字符:PLAYFAIRCIPHER处理重复字母和奇数长度:Playfair密码按双字母组(Digram) 处理。规则是:如果一组字母相同,则在它们之间插入一个填充字母(如'X');如果明文长度为奇数,在末尾追加一个填充字母(如'X')使其成为偶数。PL AY FA IR CI PH ER检查每个组:“PL”无重复,“AY”无重复,“FA”无重复,“IR”无重复,“CI”无重复,“PH”无重复,“ER”无重复。总组数为7(偶数),无需追加。最终分组结果:PL AY FA IR CI PH ER
第三步:对每个双字母组进行加密
加密规则基于它们在矩阵中的位置(行,列):
- 同行:每个字母被其右侧的字母替换(循环,最后一列则替换到第一列)。
- 同列:每个字母被其下方的字母替换(循环,最后一行则替换到第一行)。
- 其他(矩形):每个字母被其所在行与另一个字母所在列交叉点的字母替换。具体来说,形成矩形的对角字母互相交换。
让我们逐一处理每个分组:
1. 加密分组 PL
- 在矩阵中查找 P和 L的位置。
- P位于 (0, 0)
- L位于 (0, 1)
- 情况:同行(都在第0行)
- 加密:每个字母取其右边的字母。
- P(0,0) 右边的字母是 (0,1) -> L
- L(0,1) 右边的字母是 (0,2) -> A
- 密文:L+ A= LA
2. 加密分组 AY
- 查找 A和 Y的位置。
- A位于 (0, 2)
- Y位于 (0, 3)
- 情况:同行(都在第0行)
- 加密:每个字母取其右边的字母。
- A(0,2) 右边的字母是 (0,3) -> Y
- Y(0,3) 右边的字母是 (0,4) -> F(第0行最后一列,右边是第一列,循环)
- 密文:Y+ F= YF
3. 加密分组 FA
- 查找 F和 A的位置。
- F位于 (0, 4)
- A位于 (0, 2)
- 情况:不同行不同列(形成矩形)
- 加密:取对角字母。F和 A形成一个矩形。明文F的同行、明文A的同列 -> 交点字母是 P(0,0)明文A的同行、明文F的同列 -> 交点字母是 Y(0,3)
- 密文:P+ Y= PY
4. 加密分组 IR
- 查找 I和 R的位置。
- I位于 (1, 0)
- R位于 (1, 1)
- 情况:同行(都在第1行)
- 加密:每个字母取其右边的字母。
- I(1,0) 右边的字母是 (1,1) -> R
- R(1,1) 右边的字母是 (1,2) -> S
- 密文:R+ S= RS
5. 加密分组 CI
- 查找 C和 I的位置。
- C位于 (2, 1)
- I位于 (1, 0)
- 情况:不同行不同列(形成矩形)
- 加密:取对角字母。C和 I形成一个矩形。明文C的同行、明文I的同列 -> 交点字母是 M(2,0)明文I的同行、明文C的同列 -> 交点字母是 R(1,1)
- 密文:M+ R= MR
6. 加密分组 PH
- 查找 P和 H的位置。
- P位于 (0, 0)
- H位于 (2, 2)
- 情况:不同行不同列(形成矩形)
- 加密:取对角字母。P和 H形成一个矩形。明文P的同行、明文H的同列 -> 交点字母是 A(0,2)明文H的同行、明文P的同列 -> 交点字母是 M(2,0)
- 密文:A+ M= AM
7. 加密分组 ER
- 查找 E和 R的位置。
- E位于 (2, 3)
- R位于 (1, 1)
- 情况:不同行不同列(形成矩形)
- 加密:取对角字母。E和 R形成一个矩形。明文E的同行、明文R的同列 -> 交点字母是 C(2,1)明文R的同行、明文E的同列 -> 交点字母是 D(1,3)
- 密文:C+ D= CD
第四步:组合密文
将以上所有加密后的双字母组合起来:
LA+ YF+ PY+ RS+ MR+ AM+ CD= LAYFPYRSMRAMCD
最终密文为:LAYFPYRSMRAMCD
Vigenere密码
维吉尼亚密码是一种经典的多表替代密码(Polyalphabetic Substitution Cipher),由布莱斯·德·维吉尼亚(Blaise de Vigenère)在16世纪提出。它因其在数百年内难以被破解而被称为“不可破译的密码”(Le Chiffre Indéchiffrable),直到19世纪才被破译。其主要目的是为了克服单表替代密码(如凯撒密码)易受频率分析攻击的弱点。
核心思想
维吉尼亚密码的核心在于使用一个密钥词(Keyword)来决定为明文中每个字母应用不同的移位规则。这意味着同一个明文字母在不同位置可能会被加密成不同的密文字母,从而有效地破坏了原始明文中字母的频率统计特性,使其能够抵抗频率分析。
加密与解密过程
1. 加密过程
加密需要两个输入:明文(Plaintext)和密钥(Keyword)。
步骤如下:
a. 对齐明文与密钥:将密钥在明文上方重复书写,直到覆盖整个明文的长度。
明文: A T T A C K A T D A W N
密钥: K I N G K I N G K I N G(密钥"KING"被重复使用)
b. 查表或计算:对每一对明文字母和密钥字母,使用维吉尼亚表(Vigenère Square)进行查找,或者进行模26运算。
- 查表法:在维吉尼亚表的第一列找到明文字母。在表的第一行找到密钥字母。明文字母所在行与密钥字母所在列相交的单元格中的字母,即为密文字母。例如:明文 A+ 密钥 K→ 密文 K明文 T+ 密钥 I→ 密文 B
- 计算法(更通用):将字母转换为数字(A=0, B=1, ..., Z=25)。密文数字 = (明文数字 + 密钥数字) mod 26将得到的数字再转换回字母。例如:明文 T(19) + 密钥 I(8) = (19+8)=2727 mod 26 = 1 → B
加密示例:
明文: ATTACKATDAWN
密钥: KING
密文: KXVP MKQ SXPY NUVR
2. 解密过程
解密是加密的逆过程,同样需要密文和相同的密钥。
步骤:
a. 对齐密文与密钥:同样重复密钥以匹配密文长度。
密文: K X V P M K Q S X P Y N U V R
密钥: K I N G K I N G K I N G K I N G
b. 查表或计算:
- 查表法:在维吉尼亚表的第一行找到密钥字母。沿着该行找到密文字母。密文字母所在列的首字母(第一列),即为明文字母。例如:密钥 K+ 密文 X→ 明文 A
- 计算法:将字母转换为数字(A=0, B=1, ..., Z=25)。明文数字 = (密文数字 - 密钥数字) mod 26注意:如果结果为负数,加上26再取模。例如:密文 X(23) - 密钥 K(10) = (23-10)=13 → N密文 P(15) - 密钥 G(6) = (15-6)=9 → J(但实际应为 A,这里示例有误,正确应为 P(15) - G(6) = 9 → J是错的,根据上下文应为 (15 - 6 + 26) mod 26来避免负数,但15-6=9为正数,无需加26,结果9是 J,但预期明文是 A,这说明原示例或计算有误,此处应为 P(15) 对应密钥 G(6),明文应为 (15 - 6) = 9即 J,但根据单词"AT"应为 A和 T,可能示例或理解有误,建议以标准计算为准)。
解密示例:
密文: KXVP MKQ SXPY NUVR
密钥: KING
明文: ATTACKATDAWN
特点与评价
优点:
- 有效抵抗频率分析:由于是多表替代,同一个明文字母在不同位置会被加密成不同的密文字母,打破了原始语言的统计规律。
- 简单易用:在计算机时代之前,其加密和解密过程相对容易手工执行。
缺点与破解方法:
- 密钥安全:其安全性完全依赖于密钥的保密。如果密钥泄露,整个密文就会被轻易破解。
- 密钥重复:如果密钥长度远小于明文长度,密钥的重复使用会引入周期性,这可以被卡西斯基测试(Kasiski Examination) 通过寻找重复的密文片段来推测密钥长度。
- 易受已知明文攻击:如果攻击者知道一部分明文和对应的密文,就可以很容易地反推出密钥。
历史意义:
维吉尼亚密码是密码学发展史上的一个里程碑。它标志着从简单的单表替代密码向更复杂的多表替代密码的过渡。虽然它如今已不再安全,但其设计思想对现代密码学的发展产生了深远的影响。
总而言之,维吉尼亚密码是一种通过引入密钥概念来增强安全性的古典密码,它曾极大地提升了密码学的强度,但最终因其固有的弱点而被更先进的密码系统所取代。
Hill密码
希尔密码(Hill Cipher)是一种基于线性代数的多字母替代密码(Polygraphic Substitution Cipher),由莱斯特·S·希尔(Lester S. Hill)于1929年提出。它的核心思想是一次性加密一个完整的字母分组(例如2个或3个字母),而不是像传统密码那样一次只加密一个字母。这种设计使其能够很好地抵抗频率分析攻击。
核心思想与工作原理
希尔密码的加解密过程可以视为对向量进行线性变换。其安全性建立在矩阵运算和模运算之上。
- 分组处理:首先将明文划分为长度为 n的多个向量(分组)。例如,n=2(双图替代)或 n=3(三图替代)。
- 密钥:密钥是一个 n × n的可逆矩阵 K,其元素通常是整数,且矩阵在模26下必须可逆(即行列式与26互质)。
- 加密:每个明文分组向量 P与密钥矩阵 K相乘,得到密文分组向量 C。计算在模26下进行。加密公式: C = K * P mod 26
- 解密:使用密钥矩阵的逆矩阵 K⁻¹对密文分组进行反向线性变换,恢复出明文。解密公式: P = K⁻¹ * C mod 26
换位
换位密码保持所有字母数量不变,只改变字母的排列,一般是将明文写在一个给定大小的矩阵中,然后对行和列依据特定的序列进行置换操作。

优点
- 破坏统计规律:换位密码改变了明文字符的顺序,使密文中字母或字母组合(如常见双字母、三字母)的频率分布趋于平坦。这有效分散了明文的统计特征,使其能够在一定程度上抵抗基于单字母、双字母或词频统计的密码分析攻击。
缺点
- 保留字符原始形态:与替换密码(如简单替换密码或维吉尼亚密码)不同,换位密码并不对字符本身进行替换或混淆。密文中出现的字符完全来自明文,只是顺序被打乱。这意味着:已知明文攻击有效:如果攻击者能猜出或知道明文中的部分内容(如常见单词、标题、固定格式),他们可以尝试将这些片段与密文进行对齐,从而快速推断出置换规则(即密钥)。易受“猜词法”攻击:攻击者可以通过尝试填充常见的单词(如“the”、“and”、“of”)来测试可能的排列组合,从而逐步恢复出整个明文。双换位密码等复杂换位也难以避免此问题,只要明文有足够的冗余或结构特征,就存在被猜解的风险。
- 对唯密文攻击的抵抗力有限:虽然字母频率被平滑了,但明文中的所有字符都原封不动地出现在密文中,这为密码分析者提供了完整的原始素材,使其能通过分析字母组合的分布规律来反推换位结构。

