采用Mayavi对BEV相机外参进行可视化

一、背景介绍

在自动驾驶和计算机视觉领域，鸟瞰图(Bird’s Eye View, BEV)是一种常用的环境感知表示方式。为了构建BEV场景，通常需要融合多个相机的数据，这就涉及到相机外参(extrinsic parameters)的准确标定。本文将介绍如何使用Mayavi这一强大的3D可视化工具，对BEV系统中的6个相机外参进行可视化，帮助开发者和研究人员直观理解和验证相机空间配置。

二、什么是外参矩阵及其重要性

相机外参矩阵是一个4x4的变换矩阵，描述了相机坐标系与世界坐标系(或车辆坐标系)之间的转换关系。它包含两个部分：

1. 旋转矩阵(3x3)：表示相机坐标系相对于世界坐标系的朝向
2. 平移向量(3x1)：表示相机原点在世界坐标系中的位置

数学表示为：

[R | t]
[0 | 1]

其中R是旋转矩阵，t是平移向量。

在BEV系统中，准确的外参矩阵至关重要，因为它决定了不同相机采集的图像如何准确地映射到统一的鸟瞰视角中。外参误差会导致图像拼接错位、物体位置计算错误等问题，直接影响感知系统的可靠性。

三、为什么需要可视化相机外参

1. 验证标定结果：通过可视化可以直观检查外参标定是否正确，各相机视角是否覆盖预期区域
2. 调试与分析：当多相机融合出现问题时，可视化帮助快速定位是哪个相机的外参存在问题
3. 系统理解：帮助新团队成员理解系统的相机配置和视野范围
4. 演示与展示：为项目演示提供直观的视觉材料

四、效果图

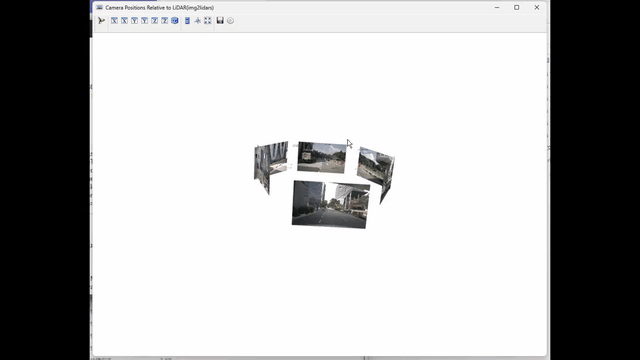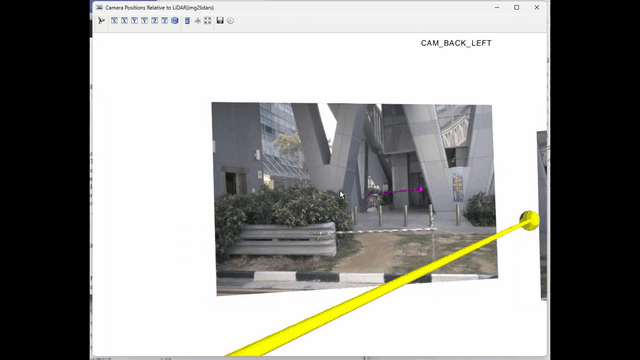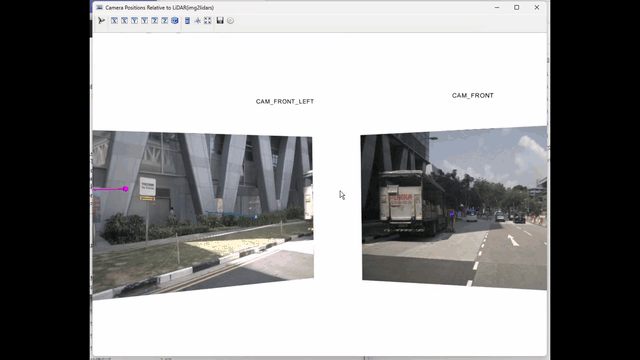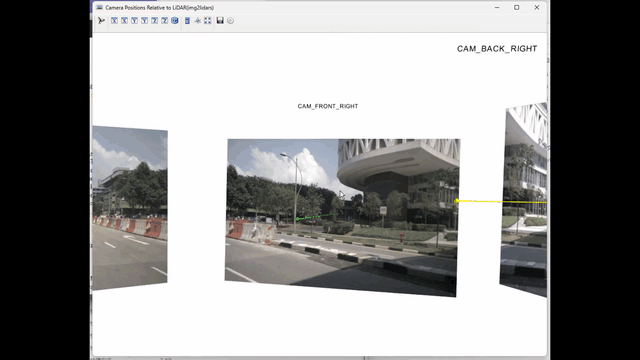
五、环境搭建

以下是实现本可视化方案所需的环境配置：

# 建议使用Python 3.8环境
https://www.python.org/ftp/python/3.8.0/python-3.8.0-amd64.exe# 升级pip
python -m pip install --upgrade pip# 安装必要的依赖库
pip install mayavi==4.7.3
pip install vtk==9.0.1
pip install configobj
pip install pyquaternion 
pip install pyqt5 
pip install numpy==1.26 
pip install matplotlib 
pip install scipy 
pip install pyyaml

六、代码实现及详解

import numpy as np
from mayavi import mlab
from pyquaternion import Quaternion
import os
import pickle# 全局变量用于控制旋转状态
current_camera_index = 0  # 当前视角指向的相机索引# 相机名称列表
CAM_NAMES = ["CAM_FRONT","CAM_FRONT_RIGHT","CAM_FRONT_LEFT","CAM_BACK","CAM_BACK_LEFT","CAM_BACK_RIGHT"
]# 相机颜色映射
CAM_COLORS = {"CAM_FRONT": (0, 0, 1),      # 蓝色"CAM_FRONT_RIGHT": (0, 1, 0), # 绿色"CAM_FRONT_LEFT": (0, 1, 1),  # 青色"CAM_BACK": (1, 0, 0),        # 红色"CAM_BACK_LEFT": (1, 0, 1),   # 洋红"CAM_BACK_RIGHT": (1, 1, 0)   # 黄色
}# 默认图像路径列表
DEFAULT_IMAGE_PATHS = ["CAM_FRONT.jpg","CAM_FRONT_RIGHT.jpg", "CAM_FRONT_LEFT.jpg","CAM_BACK.jpg","CAM_BACK_LEFT.jpg","CAM_BACK_RIGHT.jpg"
]def quaternion_to_rotation_matrix(rotation, translation):"""将四元数转换为3x3旋转矩阵，并调整平移部分参数:rotation: 四元数 [w, x, y, z] 或 [x, y, z, w]translation: 平移向量 [x, y, z]返回:4x4变换矩阵，表示从相机坐标系到世界坐标系的变换"""# 确保四元数是单位四元数q = Quaternion(rotation).normalised# 获取旋转矩阵 (从相机坐标系到世界坐标系)R_c2w = q.rotation_matrix# 计算相机中心在世界坐标系中的位置: C = -R^T * TT = np.array(translation)C = -R_c2w.T @ T# 构建从相机坐标系到世界坐标系的变换矩阵transformation_matrix = np.eye(4)transformation_matrix[:3, :3] = R_c2w   # 旋转部分transformation_matrix[:3, 3] = C        # 平移部分: 相机中心在世界坐标系中的位置return transformation_matrixdef calculate_image_corners(lidar2cam_t, R_c2w, img_width=0.5, img_height=0.3, plane_distance=0.4):"""计算相机图像平面的四个角点，考虑相机平面的倾斜参数:lidar2cam_t: 相机位置向量 [x, y, z]R_c2w: 3x3旋转矩阵，从相机坐标系到世界坐标系img_width: 图像平面宽度img_height: 图像平面高度plane_distance: 图像平面距离相机的距离返回:图像平面的四个角点坐标列表"""# 计算相机的方向向量forward_vector = R_c2w[:, 2]  # 相机的前方向（Z轴）right_vector = R_c2w[:, 0