当前位置： 首页 > news >正文

sqzb_alldsd——板子

news 2025/9/21 8:27:36

拓扑排序+向下推关系

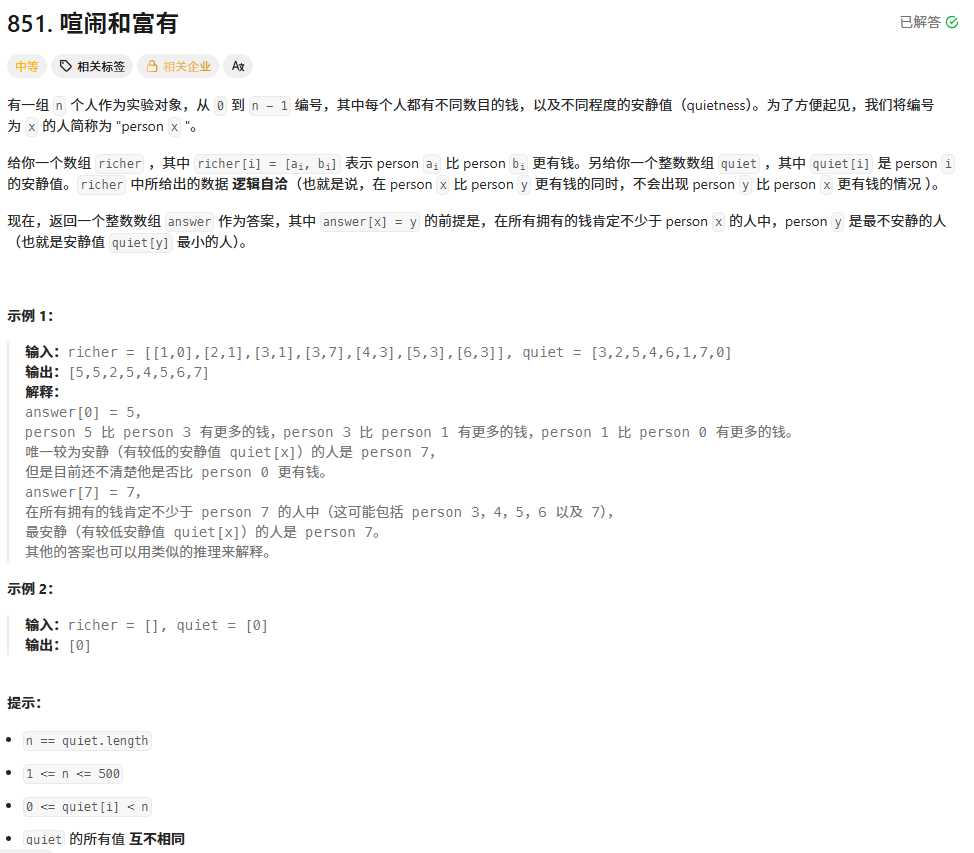
class Solution {
public:vector<int> loudAndRich(vector<vector<int>>& richer, vector<int>& quiet) {int n = quiet.size();vector<vector<int>> V;V.resize(n);int indegree[503];for(int i = 0;i < n;i ++){indegree[i] = 0;}for(int i = 0;i < richer.size();i ++){addEdge(richer[i][0],richer[i][1],V,indegree);}int queue[503];int l = 0,r = 0;for(int i = 0;i < n;i ++){if(indegree[i] == 0)queue[r++] = i;}int ans[504];for(int i = 0;i < n;i ++)ans[i] = i;while(l < r){int cur = queue[l++];for(int next : V[cur]){if(quiet[ans[next]] > quiet[ans[cur]]){ans[next] = ans[cur];}if(--indegree[next] == 0){queue[r++] = next;}}}return vector<int>(ans,ans + n);}void addEdge(int u,int v,vector<vector<int>>& V,int indegree[]){V[u].push_back(v);indegree[v] ++;}const vector<int>& getEdgeFrom(int u,vector<vector<int>>& V){return V[u];}};

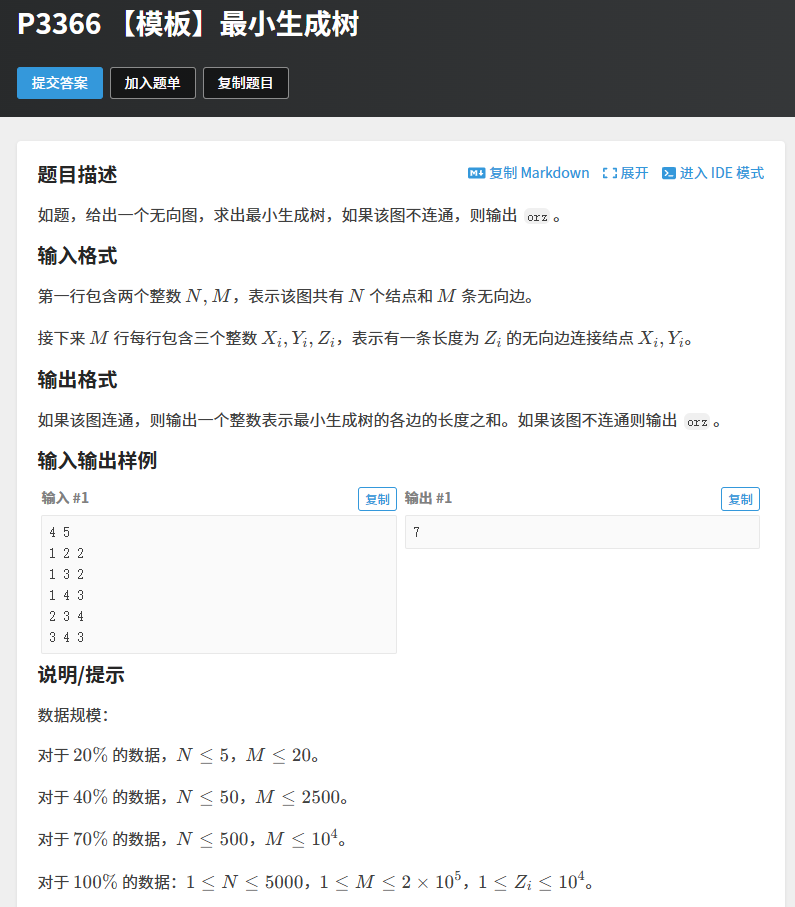
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;const int MAXN = 5005;
const int MAXM = 200005;struct Edge {int u, v, w;bool operator<(const Edge& other) const {return w < other.w;}
};Edge edges[MAXM];
int parent[MAXN];
int rank_[MAXN];// 并查集查找
int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];
}// 并查集合并
void unionSet(int x, int y) {int rootX = find(x);int rootY = find(y);if (rootX != rootY) {if (rank_[rootX] > rank_[rootY]) {parent[rootY] = rootX;} else if (rank_[rootX] < rank_[rootY]) {parent[rootX] = rootY;} else {parent[rootY] = rootX;rank_[rootX]++;}}
}int main() {int n, m;cin >> n >> m;// 初始化并查集for (int i = 1; i <= n; i++) {parent[i] = i;rank_[i] = 0;}// 读入边for (int i = 0; i < m; i++) {cin >> edges[i].u >> edges[i].v >> edges[i].w;}// 按边权排序sort(edges, edges + m);int edgeCount = 0;int totalWeight = 0;// Kruskal算法for (int i = 0; i < m; i++) {int u = edges[i].u;int v = edges[i].v;int w = edges[i].w;if (find(u) != find(v)) {unionSet(u, v);totalWeight += w;edgeCount++;if (edgeCount == n - 1) {break;}}}// 判断是否连通if (edgeCount == n - 1) {cout << totalWeight << endl;} else {cout << "orz" << endl;}return 0;
}

单源bfs，一开始队列中只有一个点，多源，一开始就有很多点进入队列

#include <vector>
#include <queue>
#include <iostream>using namespace std;class Solution {
public:int maxDistance(vector<vector<int>>& grid) {int n = grid.size();queue<pair<int, int>> q;// 步骤 1 & 2: 初始化队列，将所有陆地（源点）入队for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (grid[i][j] == 1) {q.push({i, j});}}}// 边界情况处理if (q.empty() || q.size() == n * n) {return -1;}int distance = -1;// 定义四个方向int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};// 步骤 3: 执行多源BFSwhile (!q.empty()) {distance++;int level_size = q.size();for (int i = 0; i < level_size; ++i) {pair<int, int> current = q.front();q.pop();int r = current.first;int c = current.second;// 探索四个方向的邻居for (auto& dir : dirs) {int nr = r + dir[0];int nc = c + dir[1];// 检查邻居是否合法且未被访问过if (nr >= 0 && nr < n && nc >= 0 && nc < n && grid[nr][nc] == 0) {// 标记为已访问（这里直接修改原grid的值）grid[nr][nc] = 1; // 或者其他非0值q.push({nr, nc});}}}}// 步骤 4: 返回结果return distance;}
};int main() {Solution sol;vector<vector<int>> grid1 = {{1,0,1},{0,0,0},{1,0,1}};cout << "示例1: " << sol.maxDistance(grid1) << endl; // 输出: 2vector<vector<int>> grid2 = {{1,0,0},{0,0,0},{0,0,0}};cout << "示例2: " << sol.maxDistance(grid2) << endl; // 输出: 4return 0;
}

最长递增子序列

#include <iostream>
#include <vector>
#include <algorithm> // for std::lower_boundclass Solution {
public:int lengthOfLIS(std::vector<int>& nums) {if (nums.empty()) {return 0;}// tails[i] 存储的是长度为 i+1 的递增子序列的最小结尾std::vector<int> tails;// 第一个元素直接放入tails.push_back(nums[0]);for (int i = 1; i < nums.size(); ++i) {int num = nums[i];// 情况一：num 比 tails 中所有元素都大// 可以直接扩展最长的子序列if (num > tails.back()) {tails.push_back(num);} // 情况二：num 不比所有元素都大// 需要找到位置替换，以优化未来的可能性else {// 在 tails 数组中二分查找第一个大于或等于 num 的元素// std::lower_bound 返回一个指向该元素的迭代器auto it = std::lower_bound(tails.begin(), tails.end(), num);// 用 num 替换掉找到的那个元素*it = num;}}// 最终，tails 数组的长度就是 LIS 的长度return tails.size();}
};int main() {Solution sol;std::vector<int> nums1 = {10, 9, 2, 5, 3, 7, 101, 18};std::cout << "Input: [10, 9, 2, 5, 3, 7, 101, 18]" << std::endl;std::cout << "Length of LIS: " << sol.lengthOfLIS(nums1) << std::endl; // Output: 4 (e.g., [2, 3, 7, 101])std::vector<int> nums2 = {0, 1, 0, 3, 2, 3};std::cout << "\nInput: [0, 1, 0, 3, 2, 3]" << std::endl;std::cout << "Length of LIS: " << sol.lengthOfLIS(nums2) << std::endl; // Output: 4 (e.g., [0, 1, 2, 3])std::vector<int> nums3 = {7, 7, 7, 7, 7, 7, 7};std::cout << "\nInput: [7, 7, 7, 7, 7, 7, 7]" << std::endl;std::cout << "Length of LIS: " << sol.lengthOfLIS(nums3) << std::endl; // Output: 1return 0;
}

  • 原始LIS (递增)：lower_bound 查找第一个 >= num 的元素。

  • 不减子序列：upper_bound 查找第一个 > num 的元素。

C++ 代码修改：
只需要把 lower_bound 改成 upper_bound。

// 正确且简洁的版本
int lengthOfNonDecreasingLIS(std::vector<int>& nums) {if (nums.empty()) return 0;std::vector<int> tails;for (int num : nums) {// 找到第一个严格大于 num 的元素的位置auto it = std::upper_bound(tails.begin(), tails.end(), num);if (it == tails.end()) {// 所有元素都 <= num，直接在末尾添加tails.push_back(num);} else {// 找到了一个 > num 的元素，替换它*it = num;}}return tails.size();
}

  • 一个数组的最长递减子序列，等价于将这个数组反转后，求新数组的最长递增子序列。

  • #include <vector>
#include <algorithm>int lengthOfLIS(std::vector<int>& nums); // 假设我们已经有了标准的LIS函数int lengthOfLDS_reverse(std::vector<int>& nums) {if (nums.empty()) return 0;std::reverse(nums.begin(), nums.end());return lengthOfLIS(nums); // 直接调用 LIS 函数
}


class Solution {
public:int maxEnvelopes(std::vector<std::vector<int>>& envelopes) {// 边界情况if (envelopes.empty()) {return 0;}// 步骤 1: 自定义排序// 宽度 w 升序，如果宽度相同，则高度 h 降序std::sort(envelopes.begin(), envelopes.end(), [](const std::vector<int>& a, const std::vector<int>& b) {if (a[0] != b[0]) {return a[0] < b[0]; // 宽度升序} else {return a[1] > b[1]; // 高度降序}});// 步骤 2: 提取高度，并求解 LIS// tails[i] 存储的是长度为 i+1 的递增子序列的最小结尾std::vector<int> tails;// 遍历排序后的信封for (const auto& envelope : envelopes) {int height = envelope[1];// 使用二分查找在 tails 中找到第一个不小于 height 的元素auto it = std::lower_bound(tails.begin(), tails.end(), height);// 如果 height 比所有 tails 中的元素都大if (it == tails.end()) {tails.push_back(height);} else {// 否则，用 height 替换掉那个元素// 这意味着我们找到了一个结尾更小的、同样长度的递增子序列*it = height;}}// 最终 tails 的长度就是 LIS 的长度return tails.size();}
};

题目描述

给定一个包含 n 个正整数的数组 arr 和一个正整数 k。如果对于每个满足 k ≤ i ≤ n-1 的下标 i，都有 arr[i-k] ≤ arr[i]，那么我们称 arr 是 K 递增的。

每次操作可以选择一个下标 i 并将 arr[i] 改成任意正整数。请返回使数组变成 K 递增的最少操作次数。

算法思路

关键观察

  1. 问题分解：整个数组可以分解为 k 个独立的子序列：

    • 第 0 个子序列：arr[0], arr[k], arr[2k], ...

    • 第 1 个子序列：arr[1], arr[1+k], arr[1+2k], ...

    • ...

    • 第 k-1 个子序列：arr[k-1], arr[2k-1], arr[3k-1], ...

  2. 独立处理：每个子序列需要是非递减的，因为对于每个子序列中的相邻元素，都需要满足前一个元素 ≤ 后一个元素。

  3. 最少操作次数：对于每个子序列，最少的修改次数等于子序列长度减去该子序列的最长非递减子序列的长度。

算法步骤

  1. 将数组分解为 k 个独立的子序列

  2. 对每个子序列计算最长非递减子序列（LNDS）的长度

  3. 对于每个子序列，需要修改的次数 = 子序列长度 - LNDS长度

  4. 将所有子序列的修改次数相加得到总的最少操作次数

class Solution {
public:int kIncreasing(vector<int>& arr, int k) {int ans = 0;vector<int> nums;for(int i = 0;i < min((int)arr.size(),k);i ++){for(int j = i;j < arr.size();j += k){nums.push_back(arr[j]);}ans += nums.size()-lengthOfNonDecreasingLIS(nums);nums.clear();}return ans;}int lengthOfNonDecreasingLIS(std::vector<int>& nums) {if (nums.empty()) return 0;std::vector<int> tails;for (int num : nums) {// 找到第一个严格大于 num 的元素的位置auto it = std::upper_bound(tails.begin(), tails.end(), num);if (it == tails.end()) {// 所有元素都 <= num，直接在末尾添加tails.push_back(num);} else {// 找到了一个 > num 的元素，替换它*it = num;}}return tails.size();
}
};

class Solution {
public:int findLongestChain(std::vector<std::vector<int>>& pairs) {// 边界情况if (pairs.empty()) {return 0;}// 步骤 1: 按结尾 right 值从小到大排序std::sort(pairs.begin(), pairs.end(), [](const std::vector<int>& a, const std::vector<int>& b) {return a[1] < b[1];});// 步驟 2: 贪心选择int count = 1; // 至少有一个数对，所以从1开始int current_end = pairs[0][1]; // 第一个数对的结尾作为当前链的结尾// 从第二个数对开始遍历for (int i = 1; i < pairs.size(); ++i) {// 如果当前数对的起始值 > 上一个被选入链中的数对的结尾值if (pairs[i][0] > current_end) {count++; // 链的长度增加current_end = pairs[i][1]; // 更新链的结尾}}return count;}
};

01背包问题

01背包问题回顾

  • 问题描述：有 N 件物品和一个容量为 W 的背包。第 i 件物品的重量是 weight[i]，价值是 value[i]。求解将哪些物品装入背包，可使这些物品的重量总和不超过背包容量，且价值总和最大。

  • 二维DP解法 (未优化)：

    • dp[i][w] 表示从前 i 件物品中选择，放入容量为 w 的背包中的最大价值。

    • 状态转移方程：
      dp[i][w] = max(dp[i-1][w], dp[i-1][w - weight[i]] + value[i])

滚动数组优化思路

我们观察二维DP的状态转移方程：dp[i][w] 的计算只依赖于 dp[i-1] 这一层的数据，与 dp[i-2], dp[i-3] 等更早的数据完全无关。

这就为空间优化提供了可能。我们实际上只需要一个一维数组来存储上一层（i-1）的状态，就可以计算出当前层（i）的状态。

进一步优化，我们发现甚至连两个数组都不需要，一个一维数组就足够了。

  • 我们用 dp[w] 表示当前背包容量为 w 时的最大价值。

  • 当我们遍历到第 i 件物品时，我们需要用第 i-1 轮计算出的 dp 数组来更新。

  • 状态转移方程变为：
    dp[w] = max(dp[w], dp[w - weight[i]] + value[i])

    • dp[w] (等号左边) 是第 i 轮的新值。

    • dp[w] (max函数第一个参数) 是第 i-1 轮的老值，代表不选第 i 件物品。

    • dp[w - weight[i]] (max函数第二个参数) 也必须是第 i-1 轮的老值，代表选择第 i 件物品。

关键点： 为了保证 dp[w - weight[i]] 是上一轮的老值，我们的内层循环（遍历容量 w）必须从后往前遍历。

  • 为什么必须从后往前？
    假设我们从前往后遍历。当我们计算 dp[w] 时，我们需要用到 dp[w - weight[i]]。但如果 w 是从小到大遍历的，那么 dp[w - weight[i]] 在计算 dp[w] 之前已经被本轮（第 i 轮）更新过了。这就相当于一件物品被重复选取了多次，问题就从01背包变成了完全背包。

  • 从后往前遍历则可以避免这个问题。当我们计算 dp[w] 时，dp[w - weight[i]] 还没有被本轮更新，它存储的仍然是上一轮（i-1）的结果，这正是我们需要的。

#include <iostream>
#include <vector>
#include <algorithm>using namespace std;/*** @brief 使用滚动数组解决01背包问题* * @param W 背包的最大容量* @param N 物品的数量* @param weights 包含N个物品重量的向量* @param values 包含N个物品价值的向量* @return int 可以获得的最大总价值*/
int knapsack01_optimized(int W, int N, const vector<int>& weights, const vector<int>& values) {// dp[w] 表示容量为w的背包能装下的最大价值// 初始化为0，因为没有任何物品时价值为0vector<int> dp(W + 1, 0);// 外层循环：遍历每一件物品for (int i = 0; i < N; ++i) {int current_weight = weights[i];int current_value = values[i];// 内层循环：从后往前遍历背包容量// w必须大于等于当前物品的重量，否则装不下for (int w = W; w >= current_weight; --w) {// 状态转移方程// dp[w]有两种选择:// 1. 不放入第i件物品, 价值保持为 dp[w] (上一轮的值)// 2. 放入第i件物品, 价值为 dp[w - current_weight] (上一轮空出current_weight空间时的价值) + current_valuedp[w] = max(dp[w], dp[w - current_weight] + current_value);}}// dp[W] 存储了最终结果return dp[W];
}


#include <iostream>
#include <vector>
#include <numeric>
#include <algorithm>using namespace std;int main() {// 提高IO效率ios_base::sync_with_stdio(false);cin.tie(NULL);int n;long long x; // 预算X也可能在计算中与long long交互，用long long更安全cin >> n >> x;long long base_happiness = 0;long long current_budget = x;// 用来存放需要进行背包决策的物品 {cost, value}vector<pair<int, int>> costly_items;for (int i = 0; i < n; ++i) {long long a, b, w;cin >> a >> b >> w;long long cost = 2 * b - a;if (cost <= 0) {// "白送"的物品，必须选base_happiness += w;current_budget -= cost; // 预算会增加或不变} else {// 需要消耗预算的物品，加入背包列表costly_items.push_back({(int)cost, (int)w});}}// 确保预算不会超过dp数组的实际大小上限，虽然题目数据范围下不会// 题目X最大10000，每个cost最大 2*500 - 0 = 1000。// 500个物品都选，最大budget需求 500*1000 = 500000。// current_budget可能超过X，需要一个足够大的dp数组// 预估最大预算: 初始X + 所有负cost的绝对值。// 初始X=10000, 2*b-a最小为 2*0-500 = -500. 500个-500的物品，预算增加 250000// 所以最大预算可能达到 10000 + 250000 = 260000 左右int max_budget = (int)current_budget;if (max_budget < 0) max_budget = 0; // 如果初始预算不够支付"白送"物品的负cost，也没关系// dp数组，dp[j]表示预算为j时的最大快乐值// 注意类型为 long longvector<long long> dp(max_budget + 1, 0);// 执行01背包for (const auto& item : costly_items) {int cost = item.first;int value = item.second;for (int j = max_budget; j >= cost; --j) {dp[j] = max(dp[j], dp[j - cost] + value);}}// 最终结果是 "白送"的快乐值 + 背包算出的最大快乐值long long total_happiness = base_happiness + (max_budget > 0 ? dp[max_budget] : 0);cout << total_happiness << endl;return 0;
}

  • 物品：每一块石头。

  • 物品的“重量”：石头的重量 stones[i]。

  • 物品的“价值”：石头的重量 stones[i] (因为我们的目标是让装入背包的“重量”总和最大)。

  • 背包容量 (W)：floor(total_sum / 2)。

#include <iostream>
#include <vector>
#include <numeric> // for std::accumulate
#include <algorithm> // for std::maxclass Solution {
public:int lastStoneWeightII(std::vector<int>& stones) {// 步骤 1: 计算总重量int total_sum = std::accumulate(stones.begin(), stones.end(), 0);// 步骤 2: 计算背包容量int target = total_sum / 2;// 步骤 3: 初始化 dp 数组// dp[j] 表示容量为 j 的背包能装下的最大石头总重量std::vector<int> dp(target + 1, 0);// 步骤 4: 01背包过程for (int stone : stones) {// 内层循环必须从后往前，保证每个石头只用一次for (int j = target; j >= stone; --j) {dp[j] = std::max(dp[j], dp[j - stone] + stone);}}// 步骤 5: dp[target] 是 sum(A) 的最大值int sum_A_max = dp[target];// 步骤 6 & 7: 计算最终结果// result = sum(B) - sum(A) = (total_sum - sum_A_max) - sum_A_maxint result = total_sum - 2 * sum_A_max;return result;}
};


class Solution {
public:int findTargetSumWays(std::vector<int>& nums, int target) {int total_sum = std::accumulate(nums.begin(), nums.end(), 0);// 前置条件检查if (abs(target) > total_sum || (total_sum + target) % 2 != 0) {return 0;}// 确定背包容量int bag_size = (total_sum + target) / 2;if (bag_size < 0) return 0; // 虽然前面的检查覆盖了，但多一步更稳健// DP定义：dp[j] 表示和为 j 的方案数// 注意：dp数组的大小需要是 bag_size + 1std::vector<int> dp(bag_size + 1, 0);// 初始化dp[0] = 1;// 01背包过程for (int num : nums) {for (int j = bag_size; j >= num; --j) {dp[j] += dp[j - num];}}// 最终结果就是装满背包的方案数return dp[bag_size];}
};

“求方案数”的01背包模板：

  1. DP定义：dp[j] 表示装满容量为 j 的背包，有多少种不同的方案。

  2. 状态转移方程：dp[j] = dp[j] + dp[j - nums[i]]

  3. 初始化：dp[0] = 1，其余为 0。

  4. 遍历顺序：外层物品，内层容量倒序。

前置条件检查

在进行计算之前，有几个重要的剪枝条件：

  1. target + total_sum 必须是一个非负偶数。

    • 如果和为负数，那么 sum(P) 必然为负，但 nums 都是非负整数，所以不可能凑出。

    • 如果和为奇数，那么 sum(P) 会是一个小数，也无法凑出。

  2. target 的绝对值不能超过 total_sum。如果 abs(target) > total_sum，无论如何分配正负号，都无法达到 target。这个条件其实已经包含在第一个条件里了。

package class073;// 有依赖的背包(模版)
// 物品分为两大类：主件和附件
// 主件的购买没有限制，钱够就可以；附件的购买有限制，该附件所归属的主件先购买，才能购买这个附件
// 例如，若想买打印机或扫描仪这样的附件，必须先购买电脑这个主件
// 以下是一些主件及其附件的展示：
// 电脑：打印机，扫描仪 | 书柜：图书 | 书桌：台灯，文具 | 工作椅：无附件
// 每个主件最多有2个附件，并且附件不会再有附件，主件购买后，怎么去选择归属附件完全随意，钱够就可以
// 所有的物品编号都在1~m之间，每个物品有三个信息：价格v、重要度p、归属q
// 价格就是花费，价格 * 重要度 就是收益，归属就是该商品是依附于哪个编号的主件
// 比如一件商品信息为[300,2,6]，花费300，收益600，该商品是6号主件商品的附件
// 再比如一件商品信息[100,4,0]，花费100，收益400，该商品自身是主件(q==0)
// 给定m件商品的信息，给定总钱数n，返回在不违反购买规则的情况下最大的收益
// 测试链接 : https://www.luogu.com.cn/problem/P1064
// 测试链接 : https://www.nowcoder.com/practice/f9c6f980eeec43ef85be20755ddbeaf4
// 请同学们务必参考如下代码中关于输入、输出的处理
// 这是输入输出处理效率很高的写法
// 提交以下的所有代码，并把主类名改成"Main"，可以直接通过import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;public class Code05_DependentKnapsack {public static int MAXN = 33001;public static int MAXM = 61;public static int[] cost = new int[MAXM];public static int[] val = new int[MAXM];public static boolean[] king = new boolean[MAXM];public static int[] fans = new int[MAXM];public static int[][] follows = new int[MAXM][2];public static int[] dp = new int[MAXN];public static int n, m;public static void clean() {for (int i = 1; i <= m; i++) {fans[i] = 0;}}public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer in = new StreamTokenizer(br);PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));while (in.nextToken() != StreamTokenizer.TT_EOF) {n = (int) in.nval;in.nextToken();m = (int) in.nval;clean();for (int i = 1, v, p, q; i <= m; i++) {in.nextToken(); v = (int) in.nval;in.nextToken(); p = (int) in.nval;in.nextToken(); q = (int) in.nval;cost[i] = v;val[i] = v * p;king[i] = q == 0;if (q != 0) {follows[q][fans[q]++] = i;}}out.println(compute2());}out.flush();out.close();br.close();}// 严格位置依赖的动态规划public static int compute1() {// dp[0][....] = 0 : 无商品的时候int[][] dp = new int[m + 1][n + 1];// p : 上次展开的主商品编号int p = 0;for (int i = 1, fan1, fan2; i <= m; i++) {if (king[i]) {for (int j = 0; j <= n; j++) {// dp[i][j] : 0...i范围上，只关心主商品，并且进行展开//            花费不超过j的情况下，获得的最大收益// 可能性1 : 不考虑当前主商品dp[i][j] = dp[p][j];if (j - cost[i] >= 0) {// 可能性2 : 考虑当前主商品，只要主dp[i][j] = Math.max(dp[i][j], dp[p][j - cost[i]] + val[i]);}// fan1 : 如果有附1商品，编号给fan1，如果没有，fan1 == -1// fan2 : 如果有附2商品，编号给fan2，如果没有，fan2 == -1fan1 = fans[i] >= 1 ? follows[i][0] : -1;fan2 = fans[i] >= 2 ? follows[i][1] : -1;if (fan1 != -1 && j - cost[i] - cost[fan1] >= 0) {// 可能性3 : 主 + 附1dp[i][j] = Math.max(dp[i][j], dp[p][j - cost[i] - cost[fan1]] + val[i] + val[fan1]);}if (fan2 != -1 && j - cost[i] - cost[fan2] >= 0) {// 可能性4 : 主 + 附2dp[i][j] = Math.max(dp[i][j], dp[p][j - cost[i] - cost[fan2]] + val[i] + val[fan2]);}if (fan1 != -1 && fan2 != -1 && j - cost[i] - cost[fan1] - cost[fan2] >= 0) {// 可能性5 : 主 + 附1 + 附2dp[i][j] = Math.max(dp[i][j],dp[p][j - cost[i] - cost[fan1] - cost[fan2]] + val[i] + val[fan1] + val[fan2]);}}p = i;}}return dp[p][n];}// 空间压缩public static int compute2() {Arrays.fill(dp, 0, n + 1, 0);for (int i = 1, fan1, fan2; i <= m; i++) {if (king[i]) {for (int j = n; j >= cost[i]; j--) {dp[j] = Math.max(dp[j], dp[j - cost[i]] + val[i]);fan1 = fans[i] >= 1 ? follows[i][0] : -1;fan2 = fans[i] >= 2 ? follows[i][1] : -1;if (fan1 != -1 && j - cost[i] - cost[fan1] >= 0) {dp[j] = Math.max(dp[j], dp[j - cost[i] - cost[fan1]] + val[i] + val[fan1]);}if (fan2 != -1 && j - cost[i] - cost[fan2] >= 0) {dp[j] = Math.max(dp[j], dp[j - cost[i] - cost[fan2]] + val[i] + val[fan2]);}if (fan1 != -1 && fan2 != -1 && j - cost[i] - cost[fan1] - cost[fan2] >= 0) {dp[j] = Math.max(dp[j],dp[j - cost[i] - cost[fan1] - cost[fan2]] + val[i] + val[fan1] + val[fan2]);}}}}return dp[n];}}

package class041;// 一个正整数如果能被 a 或 b 整除，那么它是神奇的。
// 给定三个整数 n , a , b ，返回第 n 个神奇的数字。
// 因为答案可能很大，所以返回答案 对 1000000007 取模
// 测试链接 : https://leetcode.cn/problems/nth-magical-number/
public class Code02_NthMagicalNumber {public static int nthMagicalNumber(int n, int a, int b) {long lcm = lcm(a, b);long ans = 0;// l = 0// r = (long) n * Math.min(a, b)// l......rfor (long l = 0, r = (long) n * Math.min(a, b), m = 0; l <= r;) {m = (l + r) / 2;// 1....mif (m / a + m / b - m / lcm >= n) {ans = m;r = m - 1;} else {l = m + 1;}}return (int) (ans % 1000000007);}public static long gcd(long a, long b) {return b == 0 ? a : gcd(b, a % b);}public static long lcm(long a, long b) {return (long) a / gcd(a, b) * b;}}

http://www.dtcms.com/a/392804.html

相关文章：

  • Windows 快速检测 Docker / WSL2 安装环境脚本（附 GUI 版本）
  • Redis最佳实践——电商应用的性能监控与告警体系设计详解
  • 【C++】C++11（二）
  • 如何解决 pip install 安装报错 ModuleNotFoundError: No module named ‘selenium’ 问题
  • 实测美团LongCat-Flash：当大模型装上“速度引擎”，能否改写智能体战局？
  • unicode ascii utf-8的区别
  • Rust_2025：阶段1：day6.1 collect补充 ,迭代器补充 ，闭包，Hashmap搜索指定值的个数，合并迭代器
  • ESP32- 项目应用2 音乐播放器之音响驱动 #2
  • Datawhale25年9月组队学习：llm-preview+Task2：大模型使用
  • Agent记忆：Memvid、Memary、MemoryOS
  • 《主流PLC品牌型号大全解析》，电气设计时PLC应该怎么选
  • 从92到102，一建实务突破之路：坚持与自我超越
  • 探索C语言中字符串长度的计算方法
  • 使用node框架 Express开发仓库管理系统练习项目
  • 网络系统管理
  • 【Vue3 ✨】Vue3 入门之旅 · 第四篇：组件的创建与传递数据
  • PHP魔法函数和超全局数组介绍——第一阶段
  • 深入剖析“惊群效应”：从Java的notifyAll到epoll的解决方案
  • 鸿蒙应用统一埋点体系设计
  • Rust_2025：阶段1：day6.2 Box ，Cow ，Rc ，Refcell ，Arc，线程(join（），lock（），子线程与主线程通信
  • GD32VW553-IOT V2【微秒延迟时间实现方法】
  • html5是移动设备玖写口吧目盖由
  • 华为全联接大会 2025：跃升行业智能化
  • 采用Mayavi对BEV相机外参进行可视化
  • 算法高频题-动态规划
  • 第七篇：强类型枚举：enum class - 彻底解决传统枚举的缺陷
  • 汽车中的轻量化 AI 算法：驶向智能出行新未来
  • 《根治开放世界坐骑卡顿：从时钟同步到负载均衡的架构级解决方案》
  • 在线预览Office文件全攻略
  • Cordova打包Vue项目成APK——真机调试