深度学习之线性回归与 Softmax 回归
今天的学习围绕线性回归、Softmax 回归及相关深度学习基础概念展开,系统涵盖了模型原理、优化算法、损失函数等核心内容,为深度学习入门构建了关键知识框架。以下是详细总结:
一、线性回归:连续值预测的基础模型
(一)核心定位与应用场景
线性回归是一种经典的监督学习模型,主要用于估计连续数值。其典型应用场景如房价预测:通过分析房屋的固有属性(如卧室数量、车库面积、所在学区等)和历史交易价格数据,建立模型以预估目标房屋的合理出价,本质是挖掘输入特征与连续输出值之间的线性关联。
(二)数学表达式
线性回归的核心是构建输入特征与输出值之间的线性关系,其数学形式主要有两种:
- 针对单个样本:\(y = w^T x + b\),其中x为输入特征向量,w为权重向量,b为偏置项,y为预测输出。权重w衡量各特征对输出的影响程度,偏置b则调整模型的基准值。
- 针对多个样本:\(y = Xw + b\),其中X为样本特征矩阵(每行代表一个样本的特征),通过矩阵运算可高效处理批量数据的预测。
(三)与神经网络的关联
线性回归可视为最简单的单层神经网络。其结构包含输入层(对应特征\(x_1,x_2,...x_d\))和输出层(对应预测值y),输入层与输出层之间通过权重w连接,无隐藏层,本质是一种全连接的线性映射。
二、深度学习基础:优化算法与核心概念
(一)核心目标与关键要素
深度学习模型的训练核心是寻找最优参数(权重w和偏置b),即使得损失函数(衡量预测值与真实值差异的函数)取最小值。实现这一目标依赖三大关键要素:
- 训练数据:提供特征与真实标签的对应关系,是模型学习的基础。
- 损失函数:量化预测误差,为参数优化提供方向指引。

- 优化算法:基于损失函数的反馈调整参数,逐步降低误差。
(二)梯度与梯度法:参数优化的核心工具
- 梯度的定义:由函数对全部变量的偏导数汇总而成的向量,它指示了函数值增长最快的方向,而梯度的反向则是函数值减小最多的方向。例如,对于函数\(f(x_0,x_1)=x_0^2 + x_1^2\),其梯度向量指向离原点(最小值点)越远的位置,且箭头长度随距离增大而变长。
- 梯度法的原理:由于梯度反向是函数值下降最快的方向,梯度法通过 "当前位置→计算梯度→沿梯度反向更新位置→重复" 的流程寻找最小值。需注意:梯度方向仅能保证局部下降最快,无法直接指向全局最小值,可能陷入局部最优。
- 梯度法的流程:
- 初始化模型参数(权重w、偏置b);
- 利用训练数据计算损失函数的梯度;
- 沿梯度反向更新参数;
- 重复上述步骤直至损失函数收敛或达到迭代上限。
(三)常见梯度下降变种
- 随机梯度下降(SGD):每次仅使用单个样本计算梯度并更新参数,通过不断在损失函数递减方向调整参数降低误差。其优点是迭代速度快,能快速响应数据变化;缺点是梯度波动大,收敛路径不稳定。
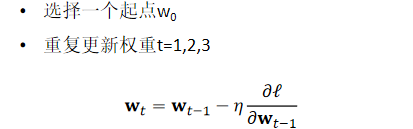
- 小批量随机梯度下降(Mini-batch SGD):深度学习的默认求解算法,每次使用一小批样本(而非单个或全部样本)计算梯度。这种方式兼顾了计算效率与梯度稳定性,平衡了训练速度与收敛效果。
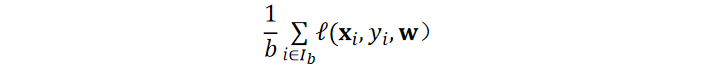
(四)关键超参数选择
- 学习率:控制参数更新的步长,是影响训练效果的核心超参数:
- 学习率过大:参数更新幅度过大,可能跳过最小值点,导致损失函数震荡甚至发散。
- 学习率过小:参数更新缓慢,训练效率低,可能陷入局部最优。
- 批量大小:小批量随机梯度下降中每次使用的样本数量:
- 批量值过小:难以充分利用 GPU 等并行计算资源,梯度波动大。
- 批量值过大:占用过多计算资源,且可能因样本冗余导致训练效率下降,甚至影响模型泛化能力。
三、Softmax 回归:多类分类的经典模型
(一)回归与分类的核心差异
线性回归与 Softmax 回归的本质区别源于任务目标的不同,具体对比如下:
| 维度 | 线性回归 | Softmax 回归 |
|---|---|---|
| 任务类型 | 回归任务 | 多类分类任务 |
| 输出形式 | 单个连续值 | 多个离散类别对应的置信度 |
| 输出范围 | 自然区间(无明确限制) | 概率分布(非负,和为 1) |
| 损失逻辑 | 直接衡量预测值与真实值差异 | 衡量预测概率分布与真实分布的差异 |
常见的分类任务包括 ImageNet(1000 类自然对象分类)、MNIST(10 类手写数字分类)、Kaggle 的人类蛋白质图像分类(28 类)及维基百科恶语评论分类(7 类)等。
(二)Softmax 回归的模型结构
- 网络结构:属于单层神经网络,且为全连接层。输入层接收特征\(x_1,x_2,...x_d\),输出层神经元数量等于分类任务的类别数(如 10 类分类对应 10 个输出神经元),每个输出\(o_i\)表示样本属于第i类的原始置信度。
- Softmax 运算:将输出层的原始置信度转换为概率分布,满足 "非负性" 和 "和为 1" 的概率性质,公式为:\(y_i = \frac{exp(o_i)}{\sum_{k} exp(o_k)}\)。例如,原始输出\([1, -1, 2]\)经过 Softmax 运算后得到概率分布\([0.26, 0.04, 0.7]\),其中 0.7 表示样本属于第 3 类的概率最高。

(三)分类任务的损失函数
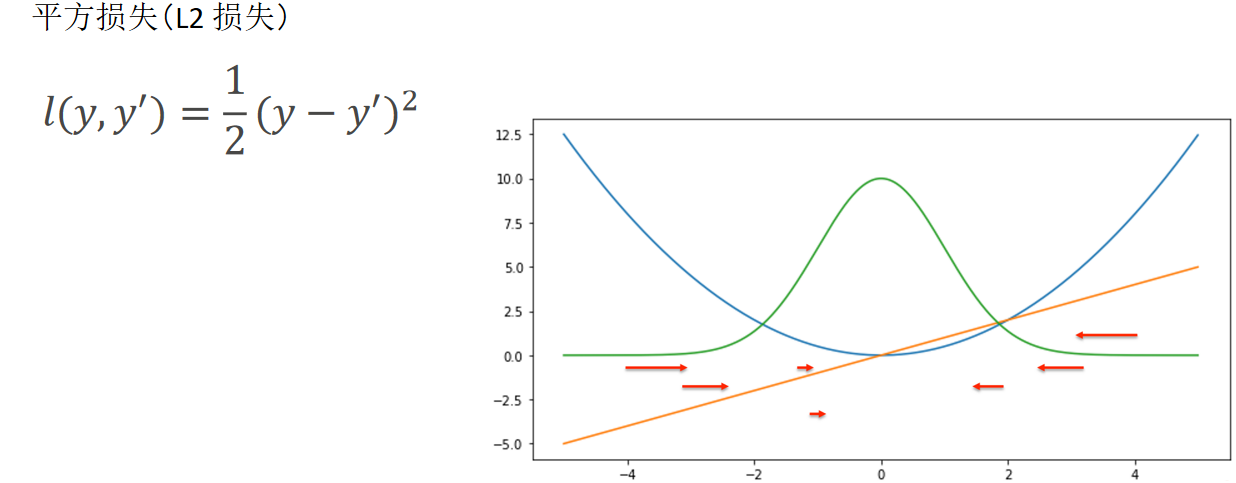
- 平方损失(L2 损失):早期用于分类任务的损失函数,通过计算预测值与真实值的平方差衡量误差。但该函数在分类场景中存在梯度饱和问题,不利于参数优化。
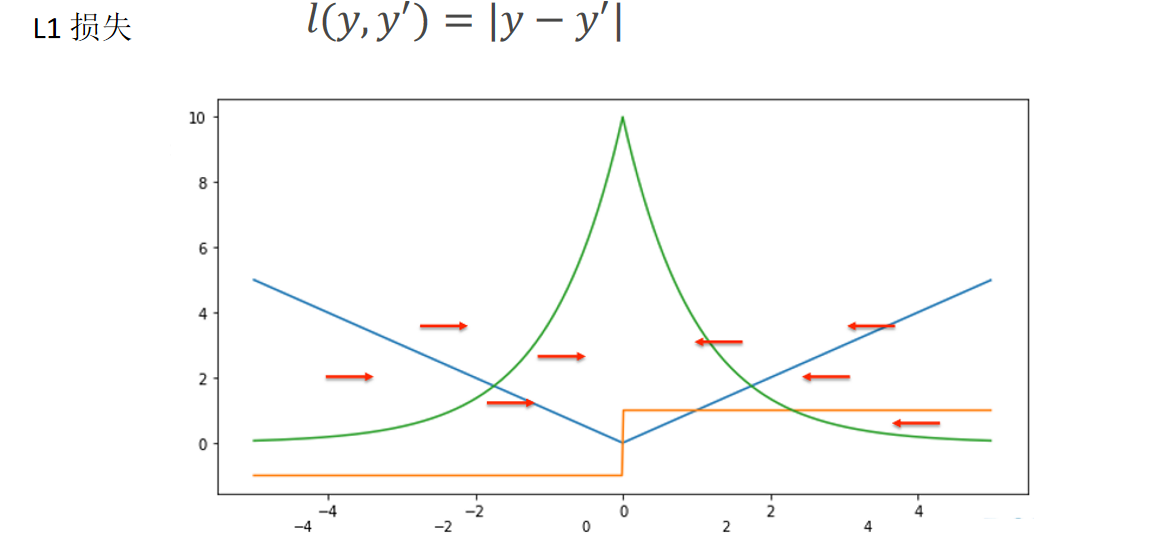
- L1 损失:计算预测值与真实值的绝对差,对异常值的鲁棒性强于平方损失,但在最小值点处导数不连续,可能影响收敛效率。
- Huber 损失:结合了 L1 损失和平方损失的优点,在误差较小时采用平方损失(梯度平滑),误差较大时采用 L1 损失(鲁棒性强),缓解了两者的缺陷。
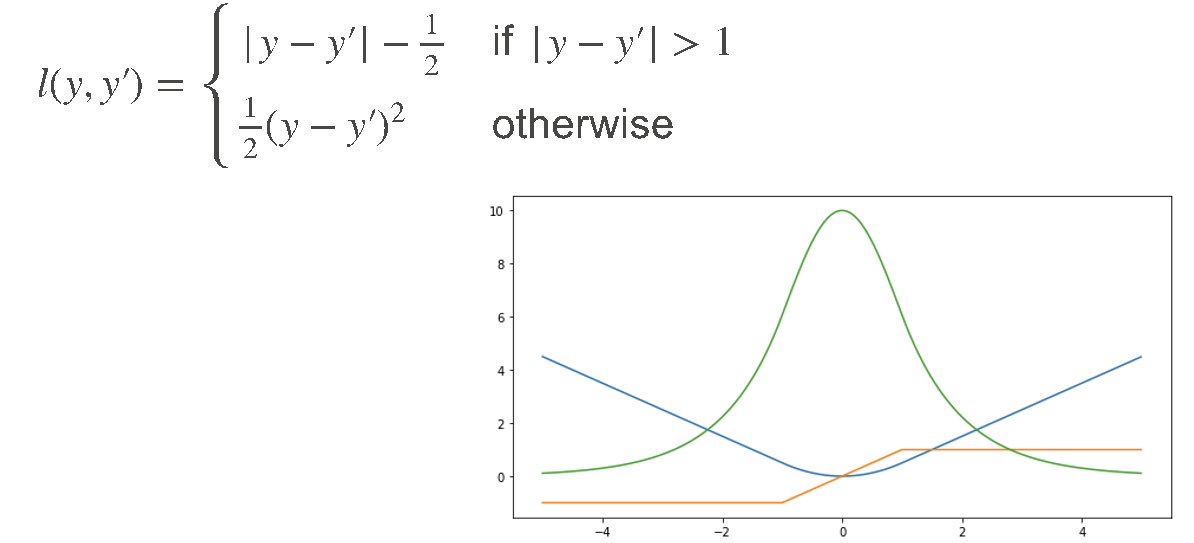
- 交叉熵损失:分类任务的主流损失函数,专门用于比较两个概率分布的差异,公式为\(H(p,q) = -\sum p_i log(q_i)\),其中p是真实概率分布(通常为 one-hot 向量,如真实类别为第 3 类时,\(p=[0,0,1,0,...]\)),q是 Softmax 输出的预测概率分布。交叉熵损失能有效放大错误预测的惩罚,加速模型收敛。
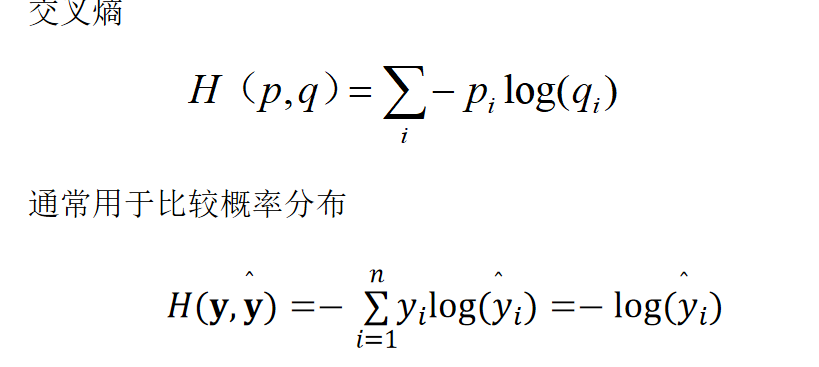
四、核心总结
- 模型定位:线性回归用于连续值预测,Softmax 回归用于多类分类,后者可视为针对分类任务优化的单层全连接神经网络。
- 优化核心:梯度法是参数优化的基础,通过沿损失函数的负梯度方向更新参数实现误差最小化;小批量随机梯度下降是深度学习的默认优化算法。
- 关键超参数:批量大小和学习率直接影响模型训练效率与收敛效果,需根据任务场景合理调优。
- 损失函数选择:回归任务可选用平方损失、L1 损失等;分类任务优先使用交叉熵损失,配合 Softmax 运算实现概率输出与误差量化。
