当前位置：首页 > news >正文

目标计数（3）Object Counting: You Only Need to Look at One

news 2025/9/18 7:17:43

论文地址：Object Counting: You Only Need to Look at One
一、摘要

本文旨在解决一次性物体计数（one-shot object counting）这一具有挑战性的任务。给定一张包含新颖的、先前未见过的类别物体的图像，该任务的目标是仅凭一个支持性的边界框示例，计数出所需类别中的所有实例。为此，我们提出了一种计数模型，您只需要查看一个实例（Look At One instance, LaoNet）。首先，一个特征相关模块结合了自注意力（Self-Attention）和相关注意力（Correlative-Attention）模块，以学习内部关系和相互关系。这使得网络对于不同实例之间旋转和尺寸的不一致性具有鲁棒性。其次，设计了一种尺度聚合（Scale Aggregation）机制，以帮助提取具有不同尺度信息的特征。与现有的少样本计数方法相比，LaoNet 在保持高收敛速度的同时，实现了最先进（state-of-the-art）的结果。

二、介绍

物体计数因其广泛的应用（如人群监控、交通监测、野生动物保护和库存管理）而变得越来越重要。大多数现有的计数方法 [1, 2, 3] 都专注于特定的单一类别。然而，当将它们应用于新类别时，它们的性能会急剧下降。同时，收集所有类别并为其标注以进行训练是极其困难和昂贵的。

对人类而言，泛化能力使我们能够在没有太多先验知识和经验的情况下学习并处理各种视觉任务。我们对这种卓越的能力感到惊讶，并在这项工作中专注于这种学习范式，设计一个网络，使其在仅给定一个示例的情况下就能有效地识别和计数新类别。我们遵循 [4] 中的少样本设置，并将其修改为一次性物体计数（one-shot object counting）。即，模型以一张包含未见过的新类别的图像和一个包含所需类别示例实例的支持边界框作为输入，然后预测图像中的物体数量。

然而，这存在两个主要挑战。首先，物体计数任务包含许多不同的类别，甚至同一图像中存在多个类别。此外，在少样本设置中，这些类别在训练和推理阶段不会重叠。这意味着模型需要具备强大的区分不同类别特征的能力，同时还需要具备对同一类别实例进行有效关联的能力。其次，在一次性计数中，模型仅从一个支持实例中学习。大部分困难源于这样一个事实：支持样本可能在其他实例（例如，大小和姿态）上有所不同。因此，要求模型在面对这些变化时保持不变性，而无需看到不同实例之间的共性。

因此，在本文中，我们提出了一个名为 LaoNet 的有效网络用于一次性物体计数。它由三个主要部分组成：特征提取、特征相关和密度回归器，如图1所示。特征相关模型和特征提取模型经过精心设计，以解决上述两个挑战。

我们提出了基于自注意力（Self-Attention）和相关注意力（Correlative-Attention）模块的特征相关模块，分别学习内部关系和相互关系。自注意力鼓励模型更多地关注重要特征及其相关性，提高了信息提炼的效率。先前的少样本计数方法 [4, 5] 通常利用卷积操作来匹配图像特征和支持特征之间的相似性。然而，由于卷积核是从具有默认大小和旋转角度的支持特征中推导出来的，该操作将在很大程度上依赖于支持特征的质量以及不同实例间物理属性的一致性。相反，我们设计的特征相关模型受益于两种注意力模块，并通过考虑所有相关性来解决上述问题。

我们进一步在尺度提取中提出了一种尺度聚合（Scale Aggregation）机制，以处理不同类别和不同实例之间的尺度变化。通过从多子空间学习特征，该模型在保持空间一致性的同时聚合了各种尺度信息。

总而言之，我们的贡献有三方面。

我们设计了一个名为 LaoNet（一个您只需要查看一个实例的网络）的新颖网络，用于一次性物体计数。通过结合自注意力和相关注意力模块，LaoNet 以高精度和高效率挖掘新类别物体之间的相关性。
我们提出了一种尺度聚合机制，以提取更全面的特征并融合来自支持框的多尺度信息。
实验结果表明，我们的模型在 FSC-147 [4] 和 COCO [6] 数据集上的一次性设置（无需微调）中取得了最先进（state-of-the-art）的结果，并有显著提升。

简要总结

本段是一篇关于一次性物体计数（One-shot Object Counting）的论文引言，提出了名为LaoNet的解决方案。

研究背景与问题：
- 重要性：物体计数应用广泛（监控、交通、生态等）。
- 现有方法局限：大多数方法只能处理单一特定类别，泛化到新类别时性能急剧下降，且为所有类别收集标注数据成本极高。
- 灵感来源：人类的强大泛化能力，只需一个例子就能学习新概念。
任务定义：一次性物体计数。模型输入为：1) 一张包含未知类别物体的图像，2) 该类别中一个实例的边界框（支持示例）。输出是该类别在图像中的总数量。
核心挑战：
- 挑战一（区分与关联）：需要同时区分不同类别的物体，并关联同一类别的实例，且训练和测试的类别完全不重叠。
- 挑战二（实例差异）：仅凭一个示例，模型必须克服同类物体在大小、姿态等方面的巨大差异。
解决方案（LaoNet）：
- 整体结构：包含特征提取、特征相关、密度回归三部分。
- 创新点一（特征相关模块）：使用自注意力（捕捉图像内部特征关系）和相关注意力（匹配图像与支持示例）替代传统的卷积匹配，从而对物体的大小和旋转变化更加鲁棒。
- 创新点二（尺度聚合机制）：专门设计用于处理物体尺度变化，从多子空间提取并融合特征。
主要贡献：
- 提出了用于一次性计数的LaoNet网络。
- 引入了结合两种注意力的特征相关模块和尺度聚合机制。
- 在FSC-147和COCO数据集上取得了最先进（SOTA） 的性能。

核心思想：这篇论文的核心是解决如何让模型像人一样，仅凭一个例子就能学会计数任意新类别的物体。其关键技术是使用更强大的注意力机制来理解物体间的相似性，并有效处理尺度、旋转等变化，从而实现优异的泛化能力。

三、最近工作

物体计数方法可以简要分为两种类型。
基于检测的方法[7] 通过详尽地检测图像中的每个目标来计数物体的数量。但它们依赖于复杂的标注，例如边界框。
基于回归的方法[1, 2] 通过学习预测一个密度图来进行计数，密度图中的每个值代表目标物体在相应位置的密度。计数预测等于密度图的总和。

然而，大多数计数方法都是类别特定的，例如用于人群 [1, 2, 8, 9, 10, 11]、汽车 [3, 12]、植物 [13] 或细胞 [14, 15]。它们只专注于一个类别，当迁移到其他类别时，会失去原有的良好性能。此外，大多数传统方法通常依赖数万个实例来训练一个计数模型 [2, 8, 9, 11, 3, 12]。

为了显著减少为特定类别训练计数模型所需的样本数量，近年来，少样本计数（few-shot counting）任务得到了发展。其关键在于模型的泛化能力，即处理来自少量标注示例的新类别。研究 [16] 提出了一种用于类别无关计数（class-agnostic counting）的通用匹配网络（GMN）。然而，它仍然需要几十到几百个新类别的示例进行适应才能获得良好性能。CFOCNet 被提出用以匹配和利用同一类别内物体之间的相似性 [5]。工作 [4] 提出了一个少样本适应与匹配网络（FamNet）来学习特征相关性和少样本适应，并引入了一个名为 FSC-147 的少样本计数数据集。

当标注示例的数量减少到一个时，该任务就演变为一次性计数（one-shot counting）。在其他视觉任务中，研究人员开发了用于一次性分割（one-shot segmentation）[17] 和一次性目标检测（one-shot object detection）[18, 19] 的方法。与通常每个对象至少使用三个实例的少样本设置 [4] 相比，只有一个实例可用的一次性设置显然更具挑战性。

值得一提的是，基于检测的方法[20, 21, 22] 在少样本和一次性计数任务中表现较差。一个主要原因是它在训练阶段需要所有实例的额外且昂贵的边界框标注，而我们关注的一次性计数方法依赖于点标注（dot annotations）和仅一个支持框（supporting box）。为了进一步说明这一点，我们在第 4.3 节进行了实验，与基于检测的方法进行比较，并验证所提出的用于一次性计数的网络。

简要总结

本段是论文的相关工作（Related Work）部分，主要回顾了物体计数领域的技术路线，并定位了本文研究（一次性计数）的挑战性和创新性。

技术路线分类：
- 基于检测的方法：先检测每个实例再计数。缺点：依赖边界框标注，成本高。
- 基于回归的方法（密度图）：预测密度图再求和得到总数。这是当前主流方法，也是本文采用的基础范式。
领域发展脉络：
- 早期（类别特定）：模型只擅长一种物体（如人、车），需要大量数据训练，泛化能力差。
- 近期（少样本计数）：旨在减少对新类别数据量的需求，追求泛化能力。代表工作有GMN（需要几十上百个示例）、CFOCNet、FamNet（并发布了FSC-147数据集）。
- 本文（一次性计数）：将少样本计数推向了更极端的条件——仅需一个示例。这与一次性分割、检测等任务一样，是更具挑战性的研究方向。
为何不采用检测方法：
- 明确指出基于检测的路线不适合少样本/一次性计数任务。因为其训练需要大量边界框标注，而一次性计数方法仅需更易获取的点标注和一个支持框，成本更低。论文后续的实验部分会对此进行验证。

核心思想：这段内容通过梳理学术脉络，清晰地阐述了本研究的定位：它属于基于密度回归的范式，并站在了少样本计数研究的最前沿（一次性），同时论证了其方法（依赖点标注）相对于检测方法（依赖边界框）在标注成本上的优势。

四、方法

4.1. 问题定义
一次性物体计数包含一个训练集 $(It,st,yt)∈T(I_t, s_t, y_t) \in \mathcal{T}$ 和一个查询集 $(Iq,sq)∈Q(I_q, s_q) \in \mathcal{Q}$ ，其中的类别是互斥的。模型的每个输入包含一张图像 $I$ 和一个支持边界框 $s$ ，该边界框标注了所需类别的一个物体。在训练集中，有丰富的点标注 $y_t$ 可用于监督模型。在推理阶段，我们的目标是让模型学会使用由 $s_q$ 采样的一个支持类别实例，来计数 $I_q$ 中的新物体。

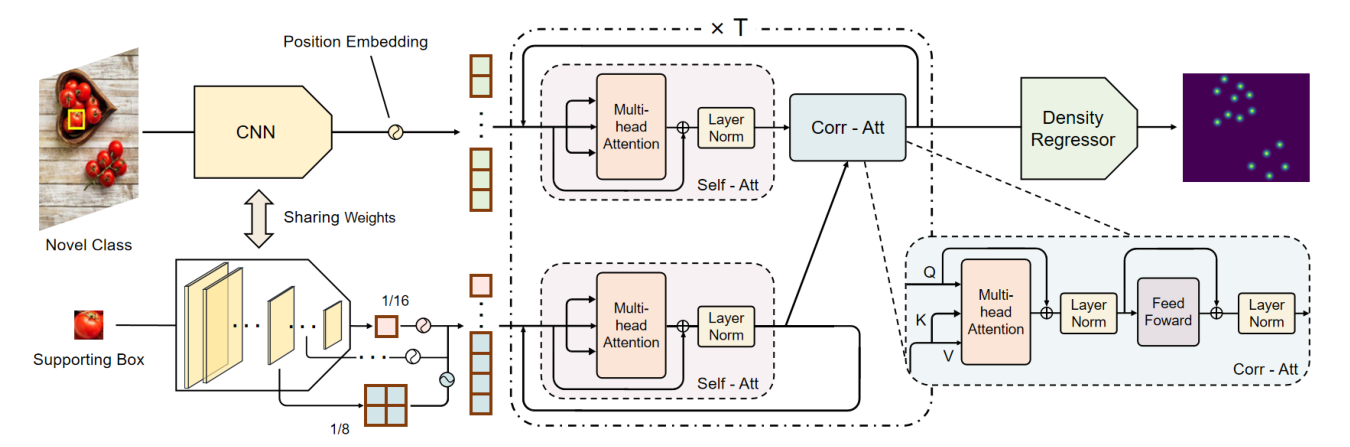
在这里插入图片描述
图1展示了所提出的LaoNet用于单样本目标计数的整体架构。查询图像和支持框都被输入到卷积神经网络（CNN）中以提取特征。支持特征在不同尺度间进行聚合。然后，带有唯一位置嵌入的扁平化特征被传输到特征关联模型中，该模型包含自注意力（Self-Attentions）和关联注意力（Correlative Attentions）。最后，采用密度回归器来预测最终的密度图。

3.2. 特征相关
由于模型需要仅从一个支持物体学习计数，因此高效地抓住特征之间的相关性至关重要。因此，我们基于自注意力（Self-Attention）和相关注意力（Correlative-Attention）模块构建了特征相关模型，分别用于学习内部关系和相互关系。

如图1（紫色块）所示，我们的自注意力模块由一个多头注意力（MA）和一个层归一化（LN）组成。我们首先介绍注意力的定义 [23]，给定查询 $Q\mathbf{Q}$ 、键 $K\mathbf{K}$ 和值向量 $V\mathbf{V}$ ：

$A(Q,K,V∣W)=Softmax((QWQ)(KWK)⊤d+PE)(VWV)\text{A}(\mathbf{Q}, \mathbf{K}, \mathbf{V} | \mathbf{W}) = \text{Softmax}\left( \frac{(\mathbf{Q}\mathbf{W}^Q)(\mathbf{K}\mathbf{W}^K)^\top}{\sqrt{d}} + \text{PE} \right) (\mathbf{V}\mathbf{W}^V)$

其中 $Softmax\text{Softmax}$ 是softmax函数， $1d\frac{1}{\sqrt{d}}$ 是基于向量维度 $d$ 的缩放因子。 $W:WQ,WK,WV∈Rd×d\mathbf{W}: \mathbf{W}^Q, \mathbf{W}^K, \mathbf{W}^V \in \mathbb{R}^{d \times d}$ 是投影的权重矩阵， $PE\text{PE}$ 是位置嵌入。

为了利用更多的表示子空间，我们采用具有多个注意力头的扩展形式：

$MA(Q,K,V)=Concat(head1,…,headh)WOwhereheadi=A(Q,K,V∣Wi)\begin{aligned} \text{MA}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) &= \text{Concat}(\text{head}_1, \dots, \text{head}_h) \mathbf{W}^O \\ \text{where} \quad \text{head}_i &= \text{A}(\mathbf{Q}, \mathbf{K}, \mathbf{V} | \mathbf{W}_i) \end{aligned}$

表示维度被并行的注意力头划分，其中参数矩阵 $Wi:WiQ,WiK,WiV∈Rd×d/h\mathbf{W}_i: \mathbf{W}_i^Q, \mathbf{W}_i^K, \mathbf{W}_i^V \in \mathbb{R}^{d \times d/h}$ 且 $WO∈Rd×d\mathbf{W}^O \in \mathbb{R}^{d \times d}$ 。

计数任务中的一个挑战性问题是存在许多复杂的干扰物。为了有效削弱这些不相关背景的负面影响，我们在图像特征中应用多头自注意力来学习内部关系，并鼓励模型更多地关注可计数的重复性物体。

我们将查询图像和支持框区域的特征序列表示为 $X\mathbf{X}$ 和 $S\mathbf{S}$ ，大小分别为 $X∈RHW×C\mathbf{X} \in \mathbb{R}^{HW \times C}$ 和 $S∈Rhw×C\mathbf{S} \in \mathbb{R}^{hw \times C}$ 。精炼后的查询特征通过以下公式计算：

$X~=LN(MA(XQ,XK,XV)+X)\tilde{\mathbf{X}} = \text{LN}( \text{MA}(\mathbf{X}_Q, \mathbf{X}_K, \mathbf{X}_V) + \mathbf{X} )$

采用层归一化（LN）来平衡数值范围。

同时，由于一次性计数问题中只有一个支持物体，精炼物体内的显著特征对于计数效率和准确性是必要且有益的。因此，我们将另一个自注意力模块应用于支持特征，并获得精炼后的 $S~\tilde{\mathbf{S}}$ 。

先前的少样本计数方法 [4, 5] 通常采用卷积操作，其中支持特征作为卷积核来匹配目标类别的相似性。然而，结果将在很大程度上依赖于支持特征的质量和物体属性（包括旋转和尺度）的一致性。

为此，我们提出了一个相关注意力模块来学习查询特征和支持特征之间的相互关系，并减轻不相关属性的约束。

具体来说，我们通过学习不同特征序列之间的相关性来扩展 MA，并添加一个前馈网络（FFN）来融合特征，即：

$X∗=Corr(X~,S~)=G(MA(X~Q,S~K,S~V)+X~)\mathbf{X}^* = \text{Corr}(\tilde{\mathbf{X}}, \tilde{\mathbf{S}}) = \mathcal{G}( \text{MA}(\tilde{\mathbf{X}}_Q, \tilde{\mathbf{S}}_K, \tilde{\mathbf{S}}_V) + \tilde{\mathbf{X}} )$

$G\mathcal{G}$ 包含两个 LN 和一个以残差形式存在的 FFN（图1中的浅蓝色块）。最终， $X∗\mathbf{X}^*$ 和 $S~\tilde{\mathbf{S}}$ 将作为新的特征序列馈入循环中，每个循环包含两个自注意力模块和一个相关注意力模块。

3.3. 特征提取与尺度聚合
为了从图像中提取特征序列，我们使用 VGG-19 作为主干网络。对于查询图像，最终层的输出被直接展平并传输到自注意力模块。对于支持框，由于透视原因实例之间存在不可控的尺度变化，我们提出了一种尺度聚合机制来融合不同的尺度信息。

给定 $l$ 作为 CNN 中的层数，我们聚合不同尺度的特征图：

$S=Concat(Fl(s),Fl−1(s),…,Fl+1−δ(s))\mathbf{S} = \text{Concat}( \mathbf{F}_l(s), \mathbf{F}_{l-1}(s), \dots, \mathbf{F}_{l+1-\delta}(s) )$

其中 $Fi\mathbf{F}_i$ 表示第 $i$ 层的特征图， $δ∈[1,l]\delta \in [1, l]$ 决定用于聚合的层数。

同时，我们利用标识位置嵌入来帮助模型在注意力模型中区分整合后的尺度信息。通过采用固定的正弦绝对位置嵌入 [23]，来自不同尺度的特征序列仍然可以保持位置之间的一致性，即：

$PE(posj,2i)=sin⁡(posj/100002i/d)PE(posj,2i+1)=cos⁡(posj/100002i/d)\begin{aligned} \text{PE}(pos_j, 2i) &= \sin(pos_j / 10000^{2i/d}) \\ \text{PE}(pos_j, 2i+1) &= \cos(pos_j / 10000^{2i/d}) \end{aligned}$

$i$ 是维度， $pos_j$ 是第 $j$ 个特征图的位置。

3.4. 训练损失
我们使用欧几里得距离来衡量估计的密度图与真实密度图之间的差异，真实密度图是根据 [1] 的方法基于标注点生成的。损失定义如下：

$LE=∥Dgt−D∥22L_E = \| \mathbf{D}_{gt} - \mathbf{D} \|_2^2$

其中 $D\mathbf{D}$ 是估计的密度图， $Dgt\mathbf{D}_{gt}$ 是真实密度图。为了提高局部模式的一致性，我们还采用了 SSIM 损失，计算遵循 [8]。通过整合以上两个损失函数，我们得到：

$L_E + \lambda L_{\text{SSIM}}$

其中 $λ\lambda$ 是平衡权重。

简要总结

本段详细描述了LaoNet网络的方法论部分，涵盖了问题定义、核心模块设计及训练细节。

问题形式化（3.1）：
- 训练集：包含图像 ( $I_t$ )、支持框 ( $s_t$ ) 和密集点标注 ( $y_t$ )。
- 查询/测试集：包含图像 ( $I_q$ ) 和支持框 ( $s_q$ )，其类别与训练集互斥。
- 目标：训练模型利用一个支持框，在推理时计数查询图像中的同类物体。
核心创新：特征相关（3.2）：
- 动机：传统方法用支持特征当卷积核，对物体尺度、旋转敏感。
- 自注意力 (Self-Attention)：用于精炼查询图像特征 ( $X~\tilde{\mathbf{X}}$ ) 和支持特征 ( $S~\tilde{\mathbf{S}}$ )，使模型关注重要区域，抑制背景干扰。
- 相关注意力 (Correlative-Attention)：核心创新。用精炼后的支持特征 ( $S~\tilde{\mathbf{S}}$ ) 作为 Key 和 Value，精炼后的查询特征 ( $X~\tilde{\mathbf{X}}$ ) 作为 Query，进行注意力计算。这实现了鲁棒的相似性匹配，减少了对物体具体形态（如旋转、尺度）的依赖。
- 循环结构：将相关注意力的输出再次输入自注意力模块，进行多次精炼。
特征提取与多尺度处理（3.3）：
- 主干网络：VGG-19。
- 尺度聚合 (Scale Aggregation)：另一核心创新。从CNN的多个不同层提取支持框的特征并将其拼接，以捕获多尺度信息。
- 位置嵌入 (PE)：使用Transformer式的正弦编码，为聚合后的多尺度特征提供位置信息，保持空间一致性。
损失函数（3.4）：
- 主损失：密度图欧几里得损失 ( $L_E$ )。
- 辅助损失：SSIM损失 ( $LSSIML_{\text{SSIM}}$ )，用于改善密度图的局部结构相似性。
- 总损失：加权和 $L_E + \lambda L_{\text{SSIM}}$ 。

核心思想：LaoNet通过注意力机制（特别是相关注意力）取代传统的卷积匹配，从而更智能、更鲁棒地衡量图像特征与支持示例之间的相似性，克服了物体在形态、尺度上的变化问题。同时，多尺度特征聚合进一步增强了模型处理尺度变化的能力。

五、实验

4.1. 实现细节与评估指标
我们通过一个上采样层和三个带有 ReLU 激活函数的卷积层来设计密度回归器。前两层的核大小为 $\times 3$ ，最后一层为 $\times 1$ 。对每张训练图像采用随机缩放和翻转。使用 Adam [24] 优化器，学习率为 $0.5 \times 10^{-5}$ 来优化参数。我们设置注意力头数 $h$ 为 4，相关循环次数 $T$ 为 2，聚合层数 $δ\delta$ 为 2，损失平衡参数 $λ\lambda$ 为 $10^{-4}$ 。

采用平均绝对误差 (MAE) 和均方根误差 (RMSE) 来衡量我们方法的性能。它们定义为：
$MAE=1M∑i=1M∣Nigt−Ni∣,RMSE=1M∑i=1M(Nigt−Ni)2,\begin{aligned} \text{MAE} &= \frac{1}{M} \sum_{i=1}^{M} |N_i^{gt} - N_i|, \\ \text{RMSE} &= \sqrt{ \frac{1}{M} \sum_{i=1}^{M} (N_i^{gt} - N_i)^2 }, \end{aligned}$
其中 $M$ 和 $N^{gt}$ 分别是图像的数量和真实计数。预测计数 $N$ 通过对估计的密度图 $D\mathbf{D}$ 积分计算得到。

4.2. 数据集
FSC-147 [4] 包含总共 6135 张图像，为少样本计数问题而收集。每张图像中，三个随机选择的对象实例用边界框标注，而其他实例用点标注。89 个对象类别共 3659 张图像被划分为训练集。分别有 29 个类别共 1286 和 1190 张图像被划分为验证集和测试集。

MS-COCO [6] 是一个大型数据集，广泛用于目标检测和实例分割。在 val2017 集中，有 80 个常见对象类别共 5000 张图像，包含复杂的日常场景。我们遵循 [17] 生成四个训练/测试分割，每个分割包含 60 个训练类别和 20 个测试类别。

4.3. 与少样本方法的比较
我们在上述两个少样本计数数据集上进行了实验，以评估所提出的网络。由于现有的专门为一次性计数设计的方法很少，为了进行全面评估，我们修改了 FamNet [4] 和 CFOCNet [5] 以适应此设置，并与其他少样本计数方法 [25, 26, 16, 27, 17] 进行了比较。

首先，表 1 显示了在 FSC-147 上的定量结果。我们列出了先前少样本检测和计数方法在 3-shot 设置下的七个结果，以及最先进的计数方法在 1-shot 设置下的两个结果以进行比较。FamNet [4] 的结果在测试期间使用了适应策略。
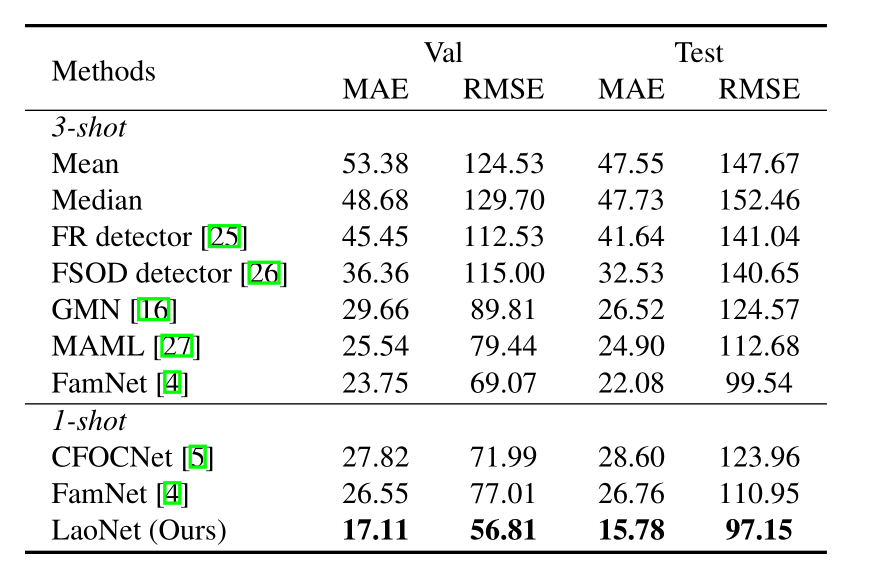在这里1111图片描述表1

值得注意的是，我们的一次性 LaoNet 优于所有先前的少样本方法，甚至是那些在 3-shot 设置下的方法，且无需任何微调策略。我们创造了新的记录，在验证集上将 FamNet 的 MAE 误差从 26.55 降低到 17.11，RMSE 从 77.01 降低到 56.81；在测试集上将 MAE 从 26.76 降低到 15.78，RMSE 从 110.95 降低到 97.15。
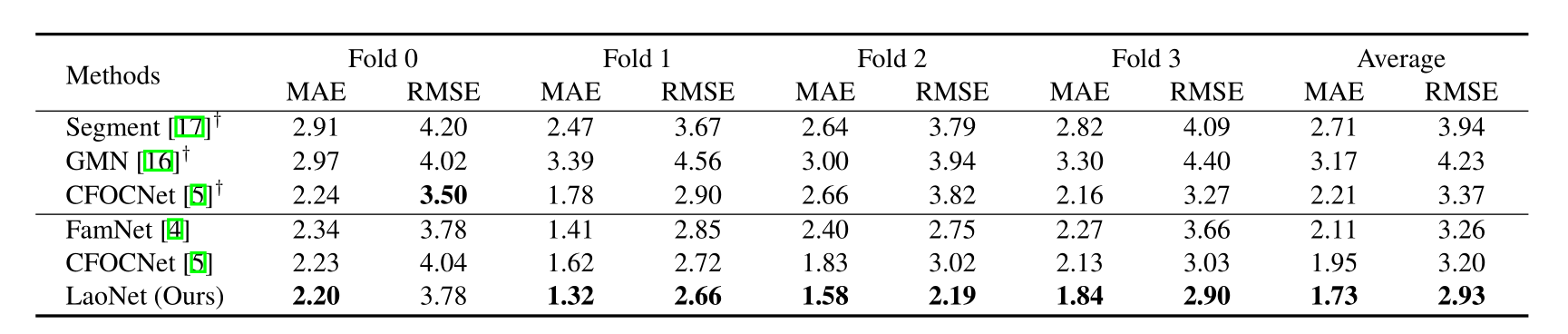
在这里插入图片描述
表2

其次，表 2 显示了在 COCO val2017 的四个分割（folds）上的结果。表中上半部分带有 $†\dagger$ 的方法遵循 [5] 中的实验设置。即，在训练和测试期间，支持示例是从数据集中的所有实例中选择的，这在需要所有实例都用边界框标注的情况下是费力且昂贵的。而我们的设置只允许每张图像有一个固定的实例，我们重新进行了 CFOCNet [5] 的实验。结果表明，我们的方法在 COCO 数据集上保持了卓越的性能。

4.4. 讨论
不同组件的贡献。我们在 FSC-147 上研究了不同组件对准确性的贡献。结果如表 3 所示，每一行报告了从 LaoNet 中移除一个组件或一个项后的结果。用于学习内部关系的两个特征序列的自注意力模块，分别将测试集的 MAE 准确率提高了 19.9% 和 15.7%，将 RMSE 提高了 9.5% 和 13.1%。与其他两项相比，自注意力模块对我们模型的性能贡献最大。
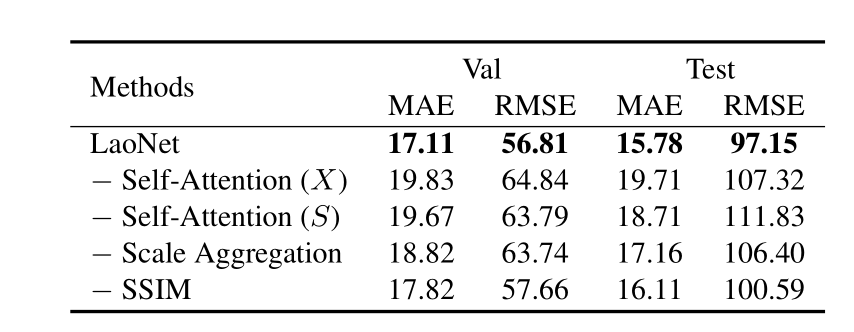
在这里插入图片描述
表3
尺度聚合机制对 RMSE 的帮助更大。结果证明了在多尺度聚合下的鲁棒性贡献。最后，SSIM 损失通过降低 MAE 和 RMSE 进一步提高了计数精度。

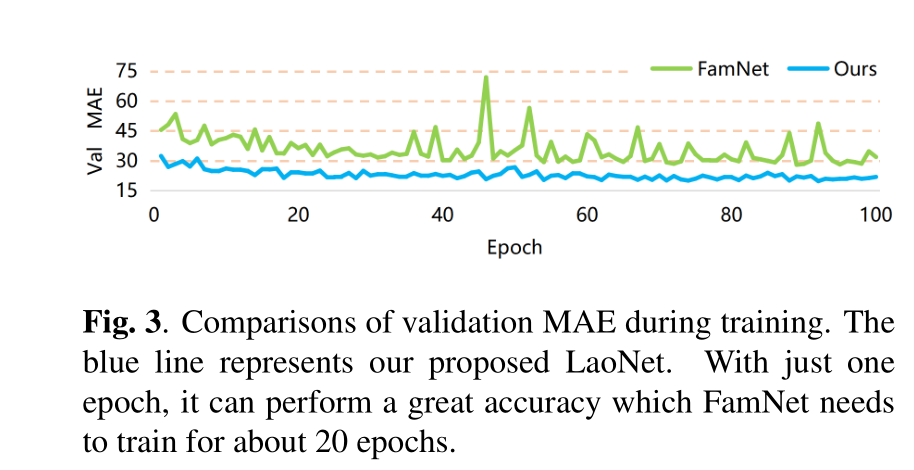
收敛速度。我们进行了实验来衡量收敛速度和性能稳定性。我们选择 FamNet [4] 作为 LaoNet 的基线，两者都使用预训练的 CNN 主干网络和 Adam 优化器。我们在 FSC-147 上训练两个模型，并报告了 100 个周期（epoch）的验证 MAE。

如图 3 所示，我们的模型比 FamNet 具有更快的收敛速度和更好的稳定性。仅用 2 个周期，我们的方法就达到了较低的计数误差，而 FamNet 需要 40 个周期才能达到。同时，我们方法的收敛过程平稳且稳定，而 FamNet 的收敛过程则起伏不定，有多个尖峰，最高误差达到 70。
在这里插入图片描述

与目标检测器的比较。目标检测器可以通过预测的检测数量来用于计数任务。然而，即使这些检测器处理的是它们训练过的类别（而非一次性设置），它们的计数性能仍然有限。我们从 FSC147 验证集和测试集中选取了与 MS-COCO 数据集共享类别的 FSC-147-COCO 子集图像，并进行了定量实验。

如表 4 所示的结果，我们将 LaoNet 与几个在 MS-COCO 上使用数千个标注示例充分预训练过的目标检测器进行了比较。然而，我们的方法（用于计数未见过的类别）仍然大幅优于那些在训练中已经见过这些类别的基于检测的方法。
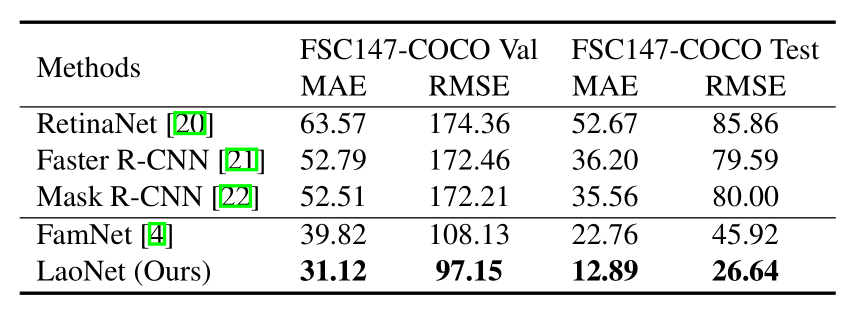
在这里插入图片描述
表4

简要总结

本段是论文的实验部分，通过大量对比和消融实验验证了LaoNet方法的有效性、高效性和优越性。

实验设置：
- 网络细节：密度回归器由1个上采样层和3个卷积层构成。
- 训练细节：使用Adam优化器，学习率 $0.5 \times 10^{-5}$ ；采用了数据增强（随机缩放和翻转）。
- 关键超参数：注意力头数 $h = 4$ ，相关循环 $T = 2$ ，聚合层数 $δ=2\delta=2$ ，损失权重 $λ=10−4\lambda=10^{-4}$ 。
- 评估指标：MAE（衡量平均误差）和RMSE（对大误差更敏感）。
数据集：
- FSC-147：少样本计数基准数据集，包含6135张图像，89/29/29个类别分别用于训练/验证/测试。
- MS-COCO：通用目标数据集，按[17]的方法划分为4个60/20类别分割，用于测试泛化性。
主要结果（SOTA性能）：
- 在FSC-147上：LaoNet在1-shot设置下的性能显著优于所有对比方法（包括它们的3-shot性能），无需任何测试时适应（fine-tuning），创造了新记录。
- 在MS-COCO上：LaoNet在更具挑战性的设置（每图仅一个固定支持实例）下，性能也大幅优于重新实验的CFOCNet等对比方法，证明了其强大的泛化能力。
分析讨论：
- 消融实验：证明了各个组件的有效性。自注意力模块贡献最大，其次是尺度聚合机制和SSIM损失。
- 收敛速度：LaoNet的收敛速度远快于FamNet（2 epoch vs. 40 epoch达到相近误差），且训练过程更稳定（误差曲线平滑无剧烈波动）。
- 与检测器对比：即使与在COCO上预训练好的成熟检测器（RetinaNet, Faster R-CNN, Mask R-CNN）相比，LaoNet在计数任务上的表现也遥遥领先。这凸显了一次性计数范式（依赖点标注）相对于检测计数范式（依赖大量边界框标注）的优越性和高效性。