线性回归与 Softmax 回归:从基础模型到深度学习入门
在深度学习的知识体系中,线性回归与 Softmax 回归是两大基石模型 —— 前者是解决连续值预测的 “入门利器”,后者则是打通 “回归到分类” 的关键桥梁。本文将结合基础原理、核心算法与实际应用场景,带你系统梳理这两个模型的核心逻辑,为深度学习进阶打下坚实基础。
一、线性回归:连续值预测的 “入门款”
线性回归的本质是 “用线性关系拟合数据,实现连续值预测”,比如根据房屋面积、地段等特征估计房价,或是根据历史销量预测未来业绩。它的核心逻辑简单易懂,却蕴含了深度学习中 “模型构建 - 损失计算 - 参数优化” 的完整流程。
1. 核心原理:用线性方程描述数据关系
线性回归的核心是构建 “输入特征” 与 “输出预测值” 之间的线性映射,最经典的单特征场景可表示为:
y = wx + b
其中,x是输入特征(如房屋面积),y是预测输出(如房价),w(权重)表示特征对输出的影响程度(面积每增加 1㎡,房价增加w元),b(偏置)是基础偏移量(无特征输入时的基准值)。
当输入包含多个特征(如房屋面积、卧室数量、距离地铁的距离)时,模型会扩展为多元线性回归,用向量形式更简洁地表示为:
y = Xw + b
这里X是特征矩阵(每行代表一个样本,每列代表一个特征),w是权重向量,通过矩阵运算实现多特征对输出的综合影响。
2. 从 “预测” 到 “优化”:损失函数与梯度下降
线性回归的目标是让 “预测值” 尽可能接近 “真实值”,这就需要通过两个关键步骤实现:定义 “误差”,再找到最小化误差的参数。
(1)损失函数:衡量预测与真实的差距
损失函数是 “量化误差” 的工具,线性回归中最常用的是均方损失(L2 损失),即计算所有样本 “预测值与真实值差值的平方和”
损失值越小,说明模型拟合效果越好 —— 我们的目标就是找到让损失函数最小的w和b。
(2)梯度下降:找到最优参数的 “导航仪”
由于无法直接通过公式求解复杂场景下的最优w和b,我们需要借助 “梯度下降” 这一优化算法,像 “走下坡路” 一样逐步逼近损失最小值。
其核心逻辑可概括为 3 步:
- 初始化参数:随机设定w和b的初始值;
- 计算梯度:梯度是 “损失函数对每个参数的偏导数汇总”,它指示了 “损失函数减小最快的方向”—— 就像指南针,告诉我们下一步往哪走能更快靠近最小值;
- 更新参数:沿着梯度反方向(因为梯度指向 “损失增大” 的方向)逐步调整参数
(3)优化升级:小批量随机梯度下降
传统梯度下降需要 “一次性计算所有样本的梯度”(即批量梯度下降),当样本量过大(如百万级)时,计算效率极低。为此,小批量随机梯度下降(Mini-batch SGD) 成为主流:
- 每次从所有样本中随机抽取一小批(如 32 个或 64 个样本);
- 基于这一小批样本计算梯度并更新参数;
- 既保证了计算效率(避免全量样本的高负载),又能通过随机性避免陷入局部最小值。
需要注意的是,小批量的 “批量大小” 也是关键超参数:太小会浪费计算资源(无法利用 GPU 并行计算),太大则会降低参数更新的灵活性,通常需根据数据量和硬件性能调整(常见取值为 32、64、128)。
3. 实际应用:从 “房价预测” 看线性回归的价值
线性回归的应用场景遍布生活与工业:
- 房地产领域:根据房屋面积、户型、地段等特征预测房价(PPT 中 “看中一个房,估计价格出价” 的场景);
- 金融领域:根据历史股价、成交量等数据预测未来股价走势;
- 电商领域:根据商品点击率、浏览时长预测用户购买概率(虽为概率,但本质是连续值预测)。
它的优势在于 “解释性强”—— 通过权重w的大小,能清晰判断每个特征的重要性(如 “卧室数量” 的权重比 “阳台面积” 大,说明卧室数量对房价影响更显著),这是很多复杂模型(如深度学习)难以替代的。
二、Softmax 回归:打通 “回归到分类” 的桥梁
线性回归解决 “连续值预测”,而现实中更多场景需要 “离散类别预测”—— 比如识别手写数字是 0-9 中的哪一个(10 分类)、判断评论是 “正面 / 负面 / 中性”(3 分类)。Softmax 回归正是为解决 “多分类问题” 而生,它在 linear 层的基础上增加了 “概率转换”,让模型能输出 “每个类别的置信度”。
1. 核心定位:从 “回归” 到 “分类” 的关键转变
先明确回归与分类的核心差异:
任务类型 | 输出形式 | 目标场景 | 示例 |
回归 | 连续值 | 预测具体数值 | 房价、销量、温度 |
分类 | 离散类别 | 预测属于哪一类 | 手写数字识别、垃圾邮件判断 |
Softmax 回归的核心作用,是将 “线性回归的连续输出” 转化为 “符合分类任务的概率输出”—— 它先通过 linear 层计算每个类别的 “原始得分”,再通过 Softmax 运算将得分转换为 “非负、和为 1” 的概率,最终选择概率最大的类别作为预测结果。
2. 两大核心步骤:先算 “得分”,再转 “概率”
(1)第一步:Linear 层计算类别得分
与线性回归类似,Softmax 回归的第一步是通过线性映射计算每个类别的 “原始得分”。假设要解决K分类问题(如 10 类手写数字识别),输入特征为X(样本数 × 特征数),则类别得分可表示为:
O = XW + b
其中O是得分矩阵(每行代表一个样本,每列代表一个类别的得分),W是权重矩阵(列数等于类别数K),b是偏置向量。
这一步的本质是 “为每个类别计算一个线性得分”,得分越高,说明样本属于该类别的 “原始置信度” 越高 —— 但此时得分可能为负、且总和不为 1,无法直接作为概率解释。
(2)第二步:Softmax 运算转换为概率
为了让 “得分” 符合 “概率” 的属性(非负、和为 1),需要通过 Softmax 函数进行转换
3. 损失计算:用交叉熵替代均方损失
分类任务的 “误差” 不能再用线性回归的均方损失 —— 均方损失对 “类别概率” 的惩罚不够精准,容易导致模型收敛慢、分类准确率低。Softmax 回归中,交叉熵损失是更优选择,它的核心是 “惩罚‘预测概率与真实标签偏差大’的情况”。
(1)交叉熵损失的核心逻辑
交叉熵原本是信息论中 “衡量两个概率分布差异” 的指标,在分类任务中,“真实标签” 可视为 “理想概率分布”(如样本属于第 3 类,则真实分布为[0, 0, 1, 0, ..., 0]),“模型预测概率” 是 “实际分布”。交叉熵损失的公式为:
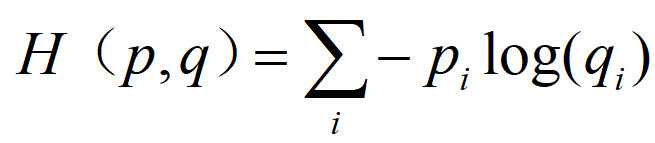
若模型对正确类别的预测概率为 1(完全准确),损失为 0;若预测概率为 0.1(严重偏差),损失为-log(0.1)≈2.3,惩罚力度显著大于均方损失。
4. 应用场景:从图像到文本的多分类任务
Softmax 回归作为 “基础分类模型”,广泛应用于各类多分类场景,也是深度学习中 “分类任务输出层” 的核心组件:
- 图像分类:MNIST 手写数字识别(10 分类)、ImageNet 自然物体分类(1000 分类),通过 Softmax 将卷积层输出的特征转换为类别概率;
- 文本分类:Kaggle 恶语评论分类(7 类,如 “toxic”“insult”“threat”),将文本的向量特征映射为不同类别评论的概率;
- 生物识别:蛋白质显微镜图像分类(28 类),辅助生物医学领域的细胞类型识别。
值得注意的是,Softmax 回归本质是 “单层神经网络”,且是 “全连接层”—— 每个类别得分的计算都依赖所有输入特征,这一特性也让它成为深度学习网络(如 CNN、Transformer)分类输出层的 “标准配置”。
三、总结:两大模型的核心价值与学习启示
线性回归与 Softmax 回归虽简单,却承载了深度学习的核心思想,总结来看有三大关键启示:
- 模型设计需 “适配任务”:连续值预测用线性回归,离散分类用 Softmax 回归 —— 模型的输出形式、损失函数必须与任务目标匹配,这是所有深度学习模型设计的基本原则;
- 优化算法是 “模型生效” 的关键:无论是线性回归还是 Softmax 回归,都依赖梯度下降(及小批量变体)实现参数优化,理解 “梯度指引方向、学习率控制步长” 的逻辑,是掌握复杂深度学习优化算法(如 Adam、RMSprop)的基础;
- 从 “简单” 到 “复杂” 的进阶路径:线性回归是 “单输出线性模型”,Softmax 回归是 “多输出线性模型 + 概率转换”,二者可视为 “单层神经网络”—— 在此基础上增加隐藏层,就能构建深度神经网络,开启更复杂的任务(如图像生成、自然语言理解)。
掌握这两个基础模型,不仅能解决实际场景中的简单预测与分类问题,更能帮你打通 “从传统机器学习到深度学习” 的思维链路 —— 后续再学习 CNN、RNN 等复杂模型时,你会发现它们的核心逻辑,依然是 “线性映射 + 非线性激活 + 梯度优化” 的延伸。
