【Leetcode hot 100】105.从前序与中序遍历序列构造二叉树
问题链接
105.从前序与中序遍历序列构造二叉树
问题描述
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
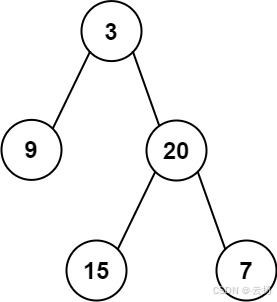
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
问题解答
解题思路
二叉树的前序遍历遵循「根 → 左 → 右」的顺序,中序遍历遵循「左 → 根 → 右」的顺序。基于这两个特性,可通过「分治思想」构造二叉树,核心步骤如下:
- 确定根节点:前序遍历的第一个元素就是当前二叉树的根节点。
- 分割左右子树:在中序遍历中找到根节点的索引,该索引左侧的元素构成左子树的中序序列,右侧构成右子树的中序序列。
- 递归构建子树:根据中序左子树的长度,可确定前序遍历中左子树和右子树的范围(前序左子树长度 = 中序左子树长度),再递归构建左、右子树。
为优化效率(避免每次在中序中线性查找根节点),可提前用哈希表存储中序序列中「元素 → 索引」的映射,将查找时间从 O(n) 降至 O(1)。
完整代码实现
import java.util.HashMap;
import java.util.Map;// 题目给定的 TreeNode 类(无需自己定义,此处为方便理解展示)
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {// 哈希表:存储中序序列的「元素-索引」映射,用于快速查找根节点位置private Map<Integer, Integer> inorderMap;// 前序数组(全局变量,避免递归时重复传参)private int[] preorder;public TreeNode buildTree(int[] preorder, int[] inorder) {// 1. 处理边界条件:若前序数组为空,直接返回空树if (preorder == null || preorder.length == 0) {return null;}// 2. 初始化全局变量this.preorder = preorder;this.inorderMap = new HashMap<>();// 填充哈希表:key=中序元素,value=元素在中序数组中的索引for (int i = 0; i < inorder.length; i++) {inorderMap.put(inorder[i], i);}// 3. 调用递归辅助函数,初始边界为整个数组的范围// 参数含义:前序左边界、前序右边界、中序左边界、中序右边界return build(0, preorder.length - 1, 0, inorder.length - 1);}/*** 递归构建二叉树的辅助函数* @param preLeft 前序序列当前子树的左边界* @param preRight 前序序列当前子树的右边界* @param inLeft 中序序列当前子树的左边界* @param inRight 中序序列当前子树的右边界* @return 当前子树的根节点*/private TreeNode build(int preLeft, int preRight, int inLeft, int inRight) {// 递归终止条件:左边界 > 右边界,说明当前子树为空if (preLeft > preRight) {return null;}// 4. 确定当前根节点(前序序列的第一个元素)int rootVal = preorder[preLeft];TreeNode root = new TreeNode(rootVal);// 5. 找到根节点在中序序列中的索引,分割左右子树int rootInIdx = inorderMap.get(rootVal);// 左子树的节点个数 = 根节点索引 - 中序左边界int leftSubtreeSize = rootInIdx - inLeft;// 6. 递归构建左子树// 前序左子树范围:[preLeft+1, preLeft + leftSubtreeSize](跳过根节点,长度=左子树节点数)// 中序左子树范围:[inLeft, rootInIdx-1](根节点左侧)root.left = build(preLeft + 1, preLeft + leftSubtreeSize, inLeft, rootInIdx - 1);// 7. 递归构建右子树// 前序右子树范围:[preLeft + leftSubtreeSize + 1, preRight](左子树之后到末尾)// 中序右子树范围:[rootInIdx+1, inRight](根节点右侧)root.right = build(preLeft + leftSubtreeSize + 1, preRight, rootInIdx + 1, inRight);// 返回当前子树的根节点return root;}
}
代码解释
- TreeNode 类:题目已定义,用于表示二叉树的节点,包含值、左子节点和右子节点。
- 全局变量:
inorderMap:存储中序序列的元素与索引映射,避免递归中重复线性查找。preorder:存储前序序列,减少递归传参开销。
- 主函数
buildTree:- 处理边界条件(空数组)。
- 初始化哈希表,填充中序序列的映射关系。
- 调用递归辅助函数,传入初始边界(整个数组范围)。
- 递归辅助函数
build:- 终止条件:左边界 > 右边界时,返回空(子树为空)。
- 取前序左边界元素作为当前根节点。
- 通过哈希表找到根节点在中序的索引,计算左子树节点数。
- 递归构建左、右子树,确定子树的前序/中序边界范围。
复杂度分析
- 时间复杂度:O(n),其中 n 为二叉树的节点数。哈希表初始化需 O(n),递归构建每个节点仅需 O(1)(哈希表查找),整体为 O(n)。
- 空间复杂度:O(n)。哈希表存储 n 个元素(O(n)),递归栈的深度最坏为 O(n)(斜树,如左链树或右链树),平均为 O(log n)(平衡树),故整体为 O(n)。
