最短路径和关键路径的算法

如下图
当我们在求下图的最短路径时，可以采用迪杰斯特拉算法和弗洛伊德算法

迪杰斯特拉算法
原理：每次比较每个顶点与起始顶点之间的权值，并找出最小权值的那一个顶点，最后，利用path数组进行反推

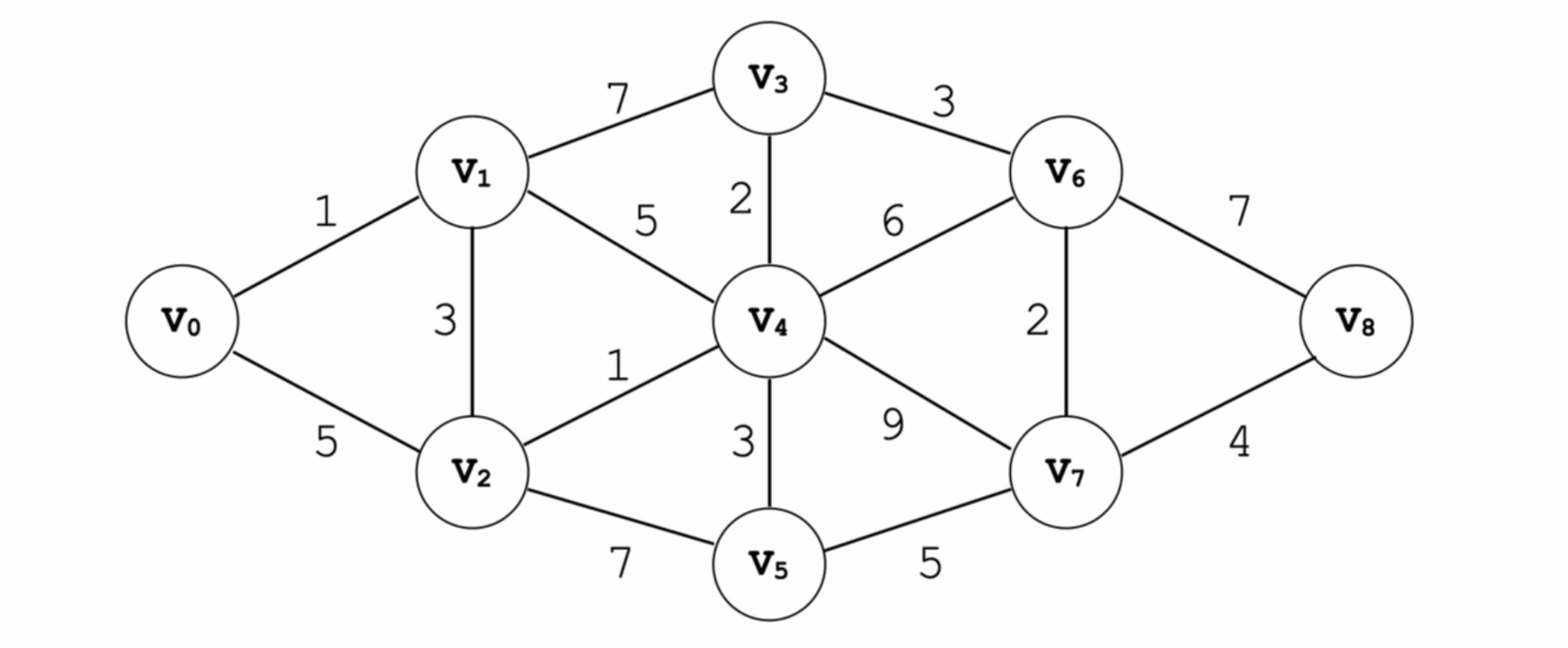
代码如下

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100
#define MAX 0x10000
typedef int VertexType;
typedef int EdgeType;
typedef struct
{VertexType vertex[MAXSIZE];EdgeType arc[MAXSIZE][MAXSIZE];int vertex_num;int edge_num;
}Mat_Graph;
void CreateGraph(Mat_Graph* G)
{G->vertex_num = 9;G->edge_num = 16;for (int i = 0;i < G->vertex_num;i++){G->vertex[i] = i;}for (int i = 0;i < G->vertex_num;i++){for (int j = 0;j < G->vertex_num;j++){if (i == j){G->arc[i][j] = 0;}else{G->arc[i][j] = MAX;}}}G->arc[0][1] = 1;G->arc[0][2] = 5;G->arc[1][2] = 3;G->arc[1][3] = 7;G->arc[1][4] = 5;G->arc[2][4] = 1;G->arc[2][5] = 7;G->arc[3][4] = 2;G->arc[3][6] = 3;G->arc[4][5] = 3;G->arc[4][6] = 6;G->arc[4][7] = 9;G->arc[5][7] = 5;G->arc[6][7] = 2;G->arc[6][8] = 7;G->arc[7][8] = 4;for (int i = 0;i < G->vertex_num;i++){for (int j = 0;j < G->vertex_num;j++){G->arc[j][i] = G->arc[i][j];}}
}
//选择顶点
int choose(int distance[], int found[], int vertex_num)
{int min = MAX;int minpos = -1;for (int i = 0;i < vertex_num;i++){if (distance[i] < min && found[i] == 0){min = distance[i];minpos = i;}}return minpos;
}
//迪杰斯特拉算法
void dijstra(Mat_Graph* G, int begin)
{int found[MAXSIZE];//确定顶点是否被遍历int path[MAXSIZE];//数组值表示距离数组下标代表的点最近的点int distance[MAXSIZE];//每一个顶点距离起始点的距离for (int i = 0;i < G->vertex_num;i++){found[i] = 0;path[i] = -1;distance[i] = G->arc[begin][i];}found[0] = 1;distance[0] = 0;int next;for (int i = 1;i < G->vertex_num;i++){next = choose(distance, found, G->vertex_num);found[next] = 1;for (int j = 0;j < G->vertex_num;j++){if (found[j] == 0){if (distance[next] + G->arc[next][j] < distance[j]){//每次替换距离值distance[j] = distance[next] + G->arc[next][j];path[j] = next;}}}}for (int i = 1;i < G->vertex_num;i++){printf("V0->V%d : %d\n", i, distance[i]);int j = i;printf("V%d<-", i);{while(path[j] != -1){printf("V%d<-", path[j]);j = path[j];}}printf("V0\n");}
}
int main()
{Mat_Graph G;CreateGraph(&G);dijstra(&G, 0);return 0;
}

运行结果如下

表示是利用path数组进行反推

弗洛伊德算法

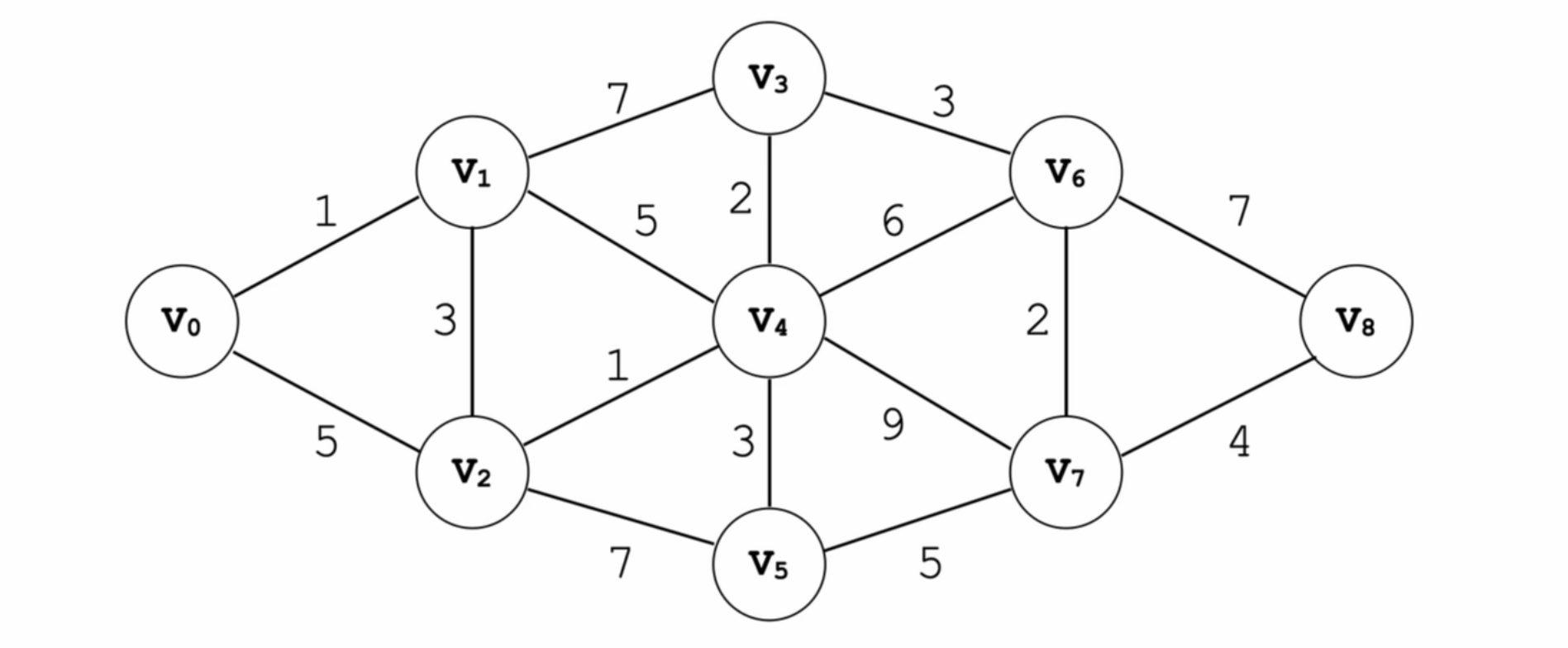
弗洛伊德算法是利用两个数组来进行判断两个顶点之间的最短路径是否经过了中间结点
代码如下

//弗洛伊德算法
void floyd(Mat_Graph* G)
{int path[MAXSIZE][MAXSIZE];//判断是否存在中间结点int distance[MAXSIZE][MAXSIZE];//两点之间的距离for (int i = 0;i < G->vertex_num;i++){for (int j = 0;j < G->vertex_num;j++){path[i][j] = j;distance[i][j] = G->arc[i][j];}}for (int i = 0;i < G->vertex_num;i++){for (int j = 0;j < G->vertex_num;j++){for (int k = 0;k < G->vertex_num;k++){if (distance[j][k] > distance[j][i] + distance[i][k]){distance[j][k] = distance[j][i] + distance[i][k];path[j][k] = path[j][i];}}}}int k;for (int i = 0;i < G->vertex_num;i++){for (int j = i + 1;j < G->vertex_num;j++){printf("V%d->V%d  weight:%d  ", i, j, distance[i][j]);k = path[i][j];printf("path:V%d->", i);while (k != j){printf("V%d->", k);k = path[k][j];}printf("V%d\n", j);}printf("\n");}
}
int main()
{Mat_Graph G;CreateGraph(&G);floyd(&G);return 0;
}

运行结果如下（只是其中i=0的一部分）