控制建模matlab练习14:线性状态反馈控制器-③极点配置
此练习,主要是使用状态空间方程来设计控制器的方法和思路:
①系统建模;
②系统的能控性;
③极点配置;
④最优化控制LQR;
⑤轨迹追踪;
以下是,第③部分:极点配置;
一、系统模型
还是以前面的①系统建模;里面的这个模型为基础进行分析。
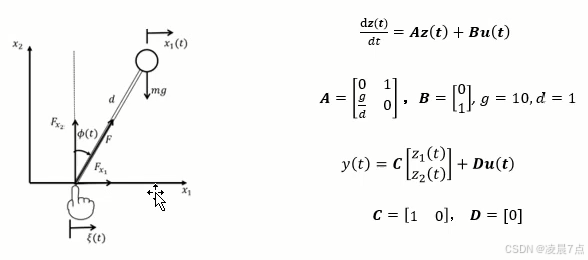
- 先介绍一下这个极点配置:(引用书中的介绍)
- 本质上说,这依然是比例控制,但相较于传统方法(只反馈位移信息),所有的状态信息(包括位移和速度)都被用作反馈,因此有两个比例增益 k1 k2 。
- 并且,状态矩阵的特征值对应于传递函数的极点。
- 所以,这种设计思路就被称为极点配置。
二、分析与控制器设计
- 书中分析这个系统,是一个不稳定的系统。若想要改变平衡点的性质,则需要设计合适的输入 u(t) ,并且在设计之前,也要先判断系统的能控性。
- 通过分析,说明只依靠输出的比例反馈控制不能满足设计要求,所以需要考虑设计全状态反馈控制器,可以令 u(t) = -Kz(t) ,其中 K=[k1 k2] 。全状态的反馈,将 z(t) 完全反馈到系统当中。
- 此时的输入 u(t) 就与所有状态变量 z(t) 有关。
- 得到闭环系统 (A - BK)z(t) = Aclz(t)
- 再通过求闭环控制系统的状态矩阵 Acl的特征值,希望两个特征值均为-1<0(此时平衡点将变成稳定节点),因此可解出 k1 、 k2 。

- 在MATLAB中的代码如下:
clc;clear;close all;
%% 定义参数g=10;d=1;
%% 定义矩阵A=[0 1;g/d 0];B=[0;1];C = [1, 0];D = 0;
%% 建立状态空间方程表达式
sys = ss(A,B,C,D);
%% 定义初始状态
z0=[pi/20;0];
%% 定义系统控制
K = [1+g/d 2];%% 此时设计好之后,再定义的闭环系统
%% 此时没有B矩阵了,B矩阵为0
sys_cl=ss(A-B*K,[0; 0],C,D);
%% 对初始条件的响应
t=0:0.01:10; %% 时间间隔
[y,t,z]=initial(sys_cl,z0,t);
%% 绘图
%% z1
subplot (2,1,1);
plot(t,z(:,1));
legend('角度:z1(t)');
grid on
%% z1
subplot (2,1,2);
plot(t,z(:,2));
legend('角速度:z2(t)');
grid on三、运行结果
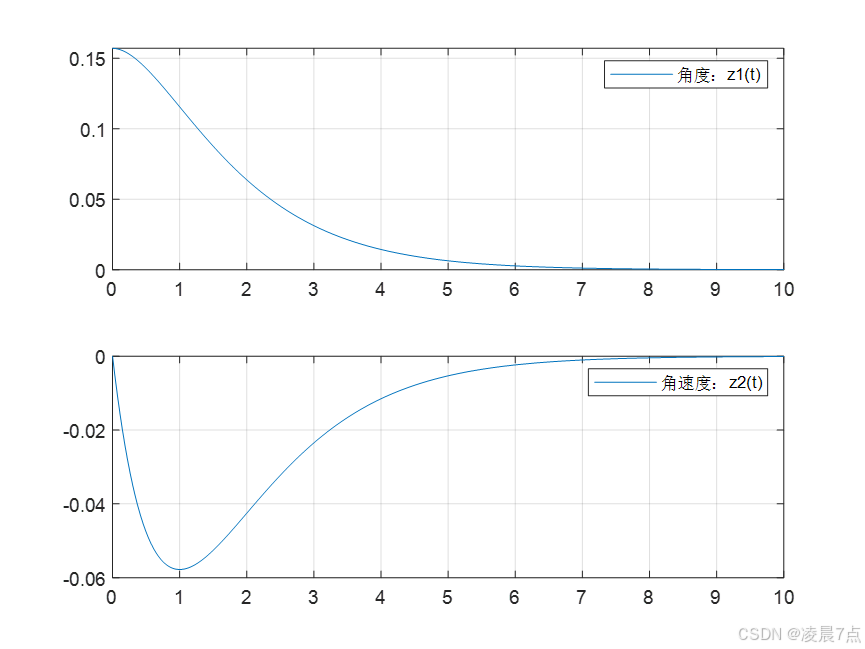
- 图中看出,角度 z1(t) ,从初始位置 π/20 开始,逐渐变成0;
- 而角速度 z2(t) ,因为初始状态就是0,所以先是向下变化,再变为0。(因为看前面模型图,角速度是要向回走,往反方向,所以是负的)
- 这里 k1 k2 的选择,将会决定系统的收敛速度和决定系统输入的值,而此练习的 k1 k2 是随机选择的。
- 如果考虑更多的条件,则需要再用到最优化控制;在下一个练习,则看如何使用最优化的思路来设计 k1 、 k2 。
学习来源:《控制之美》[卷1],王天威
