数据结构算法：顺序表

一.寄包柜

1.题目

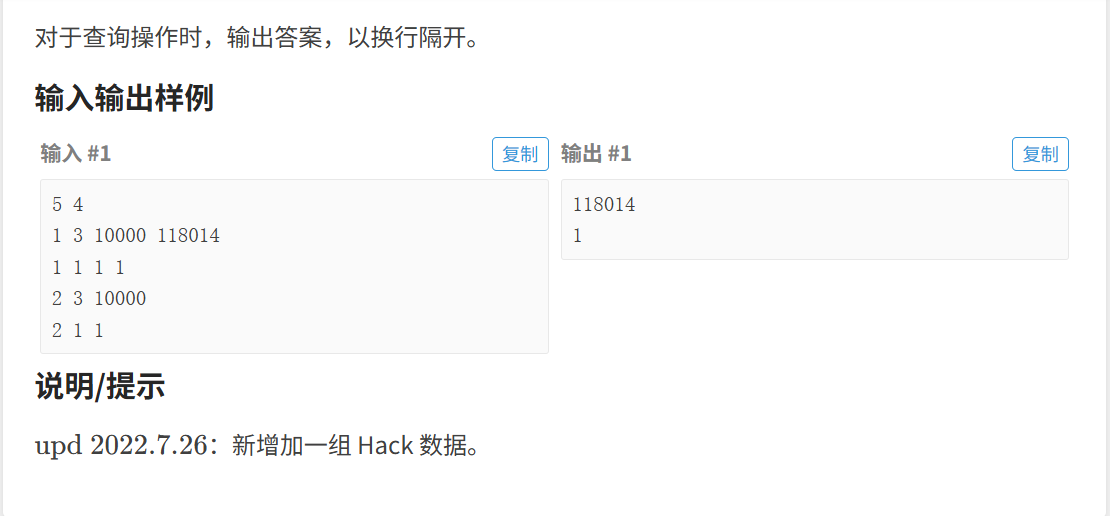
如何创建数组？

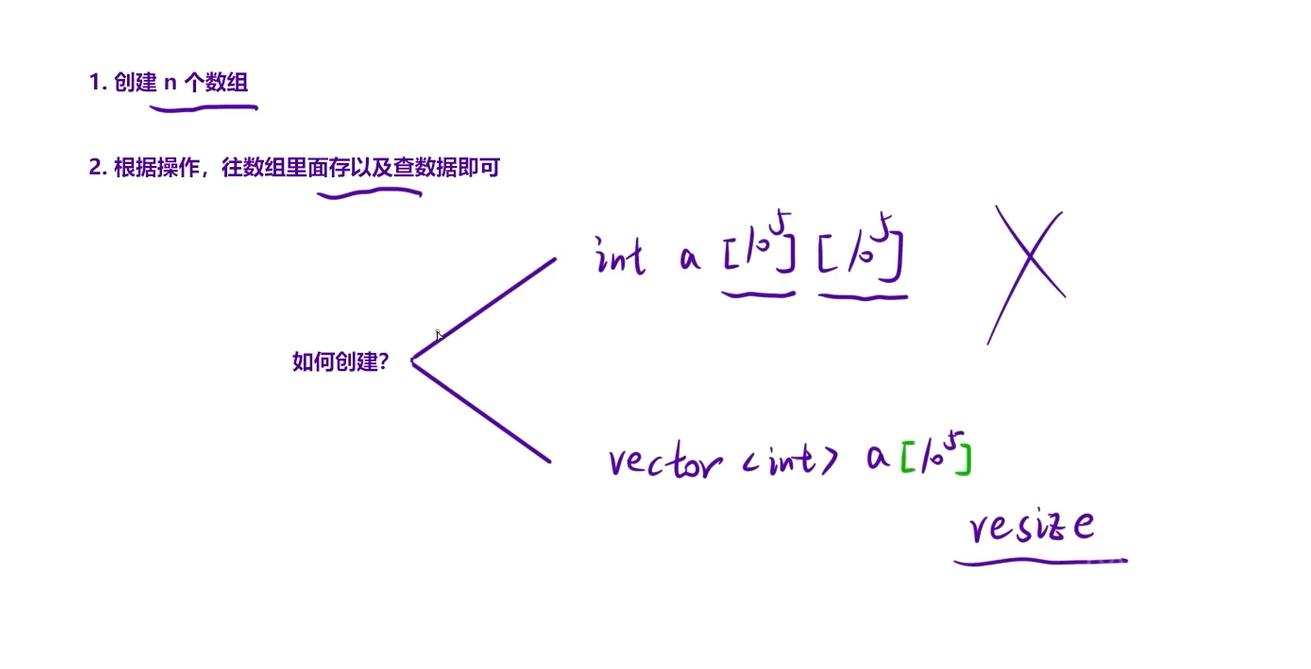
1. 需求本质

需要创建 n 个动态数组，支持：

• 按需存数据（存时扩展数组大小）
• 快速查数据（直接访问指定位置）

2. 传统静态数组的缺陷

用 int a[10^5][10^5] 这类静态二维数组：

• 内存爆炸：10^5×10^5 个 int 占约 40GB 内存（实际根本存不下）
• 无法动态扩展：数组大小编译时固定，无法适配“格子数量不确定”的需求

3. 动态方案：向量的数组

用 vector<int> a[10^5] （或题目中的 vector<int> a[N] ）：

• 每个 a[i] 是独立的 vector<int> ，支持动态扩容（用 resize 按需扩展）
• 内存更高效：只有实际存数据的 vector 会占用空间，空柜子不浪费内存

4. 核心逻辑

1. 创建结构：用 vector<int> a[MAX_N] 预分配足够的“柜子”（MAX_N 是题目给的柜子数上限，如 1e5+10 ）
2. 存数据：
   • 操作类型 1 时，检查 a[i] 当前大小 → 不够则 resize(j+1) 扩展 → 直接赋值 a[i][j] = k
3. 查数据：
   • 操作类型 2 时，直接访问 a[i][j] 输出（题目保证查询的格子“存过东西”，无需额外判断）

5. 关键优势

• 动态适配：vector 自动管理内存，存数据时按需扩容，避免静态数组的内存浪费
• 代码简洁：比手动管理指针/动态数组更简单，直接用 resize 和下标访问

总结

面对“需要 n 个动态数组”的场景，用 vector 的数组（如 vector<int> a[MAX_N] ）替代静态二维数组，通过 resize 动态扩展容量，既满足“存/查数据”需求，又能高效利用内存。

2.解题思路

2.1题目分析

题目模拟超市寄包柜场景，有 n 个寄包柜（可对应代码里的 vector<int> a[N] 结构，用数组存多个 vector 来管理不同柜子），q 次操作，操作分两种：

• 操作 1（存物品）：往第 i 个柜子的第 j 个格子存物品 k ，若格子不够就扩展柜子容量。
• 操作 2（查物品）：查询第 i 个柜子的第 j 个格子里的物品并输出。

2.2具体解题逻辑拆解步骤

1. 数据结构选择：
   用 vector<int> a[N] ，N 设为 1e5 + 10 适配题目柜子数量上限。a[i] 对应第 i 个寄包柜，用 vector 好处是可动态扩容，满足“格子数量不定、按需扩展”需求。
   比如存物品时，若柜子当前格子数不够，通过 resize 扩展，像代码里 if (a[i].size() <= j) { a[i].resize(j + 1); } ，保证能存到第 j 个格子（下标从 0 还是 1 ？看题目描述“格子编号从 1 开始”，但这里 j 直接用，实际是把格子当从 0 开始存，不过题目操作里存和查的逻辑能对应上，因为存的时候按 j 位置设值，查的时候直接取 a[i][j] ）。

2. 输入处理：
   先读 n（柜子数，虽然这里 vector<int> a[N] 直接用 N ，n 实际没约束数组大小，这里可能是题目描述里 n 范围给参考，代码写法可优化，但不影响逻辑 ）和 q（操作次数），然后循环 q 次处理每个操作。

3. 操作分支：

   • 操作 1（存物品）：读 op=1 、柜子号 i 、格子号 j 、物品 k 。先判断柜子 a[i] 当前大小够不够放 j 位置（a[i].size() <= j ），不够就扩容到 j + 1 ，然后把 a[i][j] 设为 k ，实现存物品。
   • 操作 2（查物品）：读 op=2 、柜子号 i 、格子号 j ，直接输出 a[i][j] ，因为题目保证查询的格子“存过东西”，所以不用额外判断越界（实际严谨点可加，但题目给了保证，代码就简化了 ）。

2.3总结

代码核心是用数组 + 动态数组（vector ） 组合，适配题目“柜子数量多、每个柜子格子数动态变化”的需求，通过 vector 的 resize 灵活扩容存物品，直接下标访问实现查询，逻辑简洁且能满足题目操作要求 。

2.4参考代码

#include<iostream>
#include<vector>
using namespace std;// 定义常量作为向量数组的最大容量
const int N = 1e5 + 10;//1e5 是科学计数法，表示 10^5（即 100000）int main()
{// 定义一个包含N个向量的数组，每个向量存储int类型数据vector<int> a[N];int n, q;cin >> n >> q;  // 读取数据范围和查询次数// 处理q次查询操作while (q--){int op, i, j, k;cin >> op >> i >> j;// 操作1：在第i个向量的第j个位置插入数据kif (op == 1){cin >> k;// 如果当前向量大小不足，扩展到j+1的大小if (a[i].size() <= j){a[i].resize(j + 1);}a[i][j] = k;}// 操作2：查询第i个向量的第j个位置的数据并输出else{cout << a[i][j] << endl;}}return 0;
}

二.移动零

1.题目

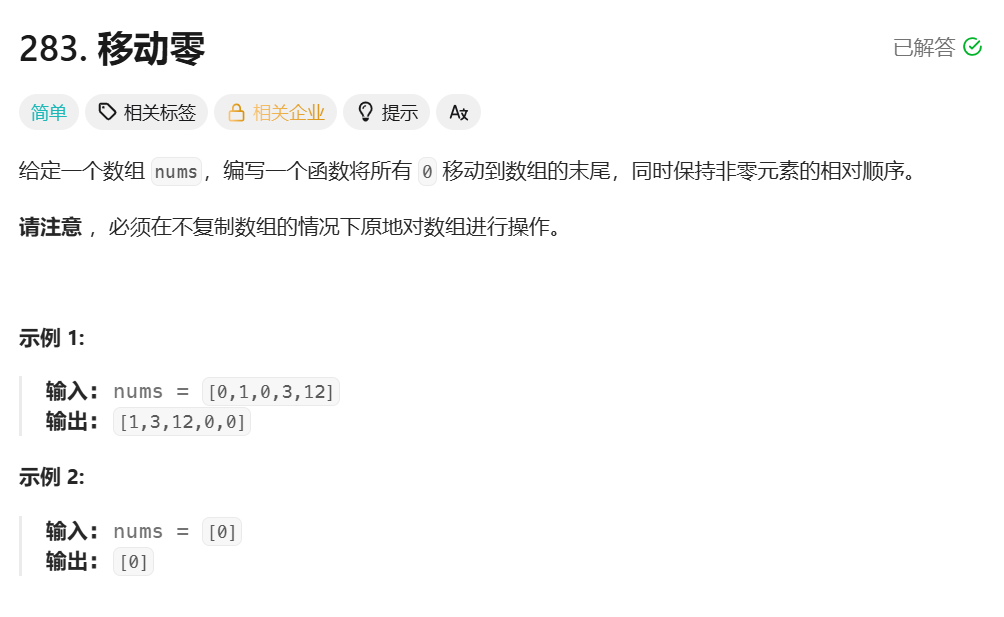
2.解题思路

---

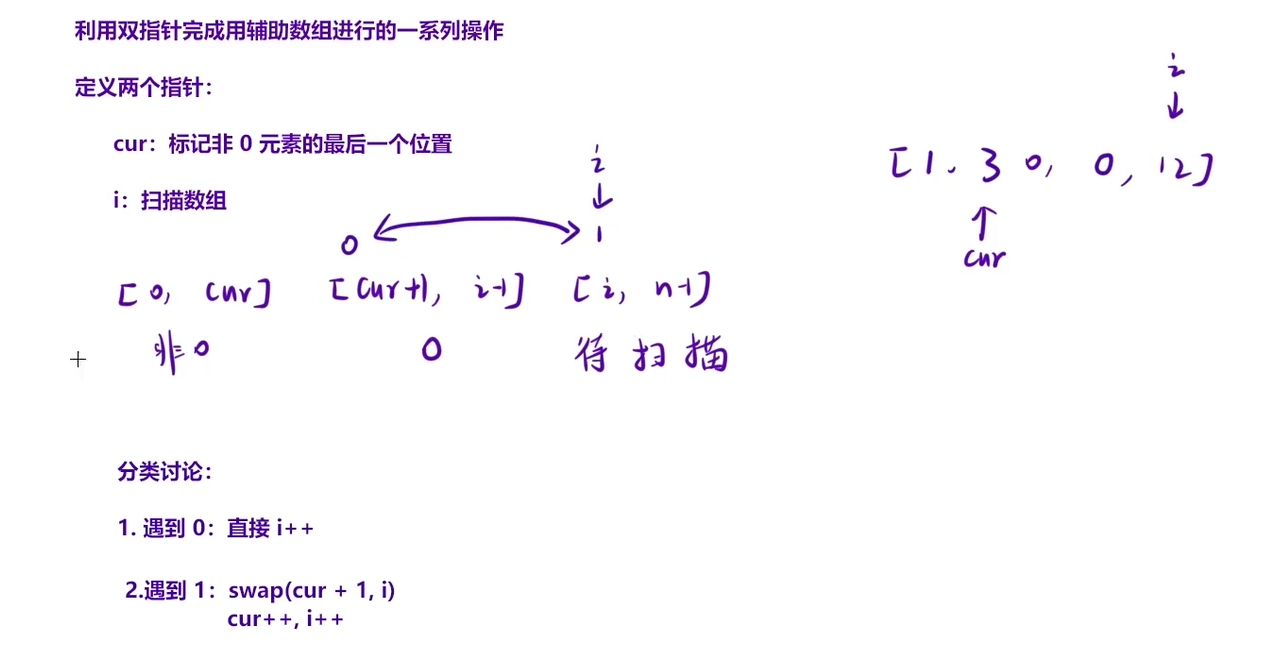
2.1解题核心思路（双指针法）

通过两个指针分工协作，原地调整数组元素位置：

• cur 指针：标记已处理好的非零元素的最后位置（初始为 -1，表示还未找到非零元素 ）。
• i 指针：遍历数组，扫描每个元素。

过程拆解：

1. 遍历数组时，i 逐个检查元素：
   • 若 nums[i] == 0：说明是待移动的零，i 直接后移（跳过零，集中处理非零）。
   • 若 nums[i] != 0：说明是需要“前移”的非零元素，执行两步：
     • 交换 nums[cur + 1] 和 nums[i]（把非零元素放到 cur 之后的位置，保证非零相对顺序）。
     • cur++（更新非零元素的最后位置），i++（继续遍历）。
2. 遍历结束后，cur 之后的位置（cur+1 到数组末尾）全填充 0（若有需要移动的零，此时已被交换到这些位置 ）。

---

2.2代码实现（C++ ）

#include<iostream>
#include <vector>
using namespace std;
class Solution {
public:void moveZeroes(vector<int>& nums) {for(int i=0,cur=-1;i<nums.size();i++)if(nums[i]) swap(nums[++cur],nums[i]);}
};

代码逻辑验证（以示例 1 为例）：
输入：nums = [0,1,0,3,12]

• 初始：cur = -1，i = 0 → nums[0] = 0 → i++（i=1）。
• i=1：nums[1] = 1 ≠ 0 → cur++（cur=0）→ 交换 nums[0] 和 nums[1] → 数组变为 [1,0,0,3,12] → i++（i=2）。
• i=2：nums[2] = 0 → i++（i=3）。
• i=3：nums[3] = 3 ≠ 0 → cur++（cur=1）→ 交换 nums[1] 和 nums[3] → 数组变为 [1,3,0,0,12] → i++（i=4）。
• i=4：nums[4] = 12 ≠ 0 → cur++（cur=2）→ 交换 nums[2] 和 nums[4] → 数组变为 [1,3,12,0,0] → i++（结束遍历）。

最终输出符合要求：[1,3,12,0,0]

---

2.3复杂度分析

• 时间复杂度：(O(n))
  只需遍历数组一次（i 从 0 到 n-1），每个元素最多被交换/访问一次，效率与数组长度线性相关。

• 空间复杂度：(O(1))
  仅用了常数级别的额外空间（cur 和循环变量 i），真正实现原地操作，符合题目要求。

---

这种双指针法是数组“原地调整”类题的经典思路，掌握后可迁移解决类似问题（如“移除元素”“排序数组中的奇偶分离”等 ）。

三.颜色分类

1.题目

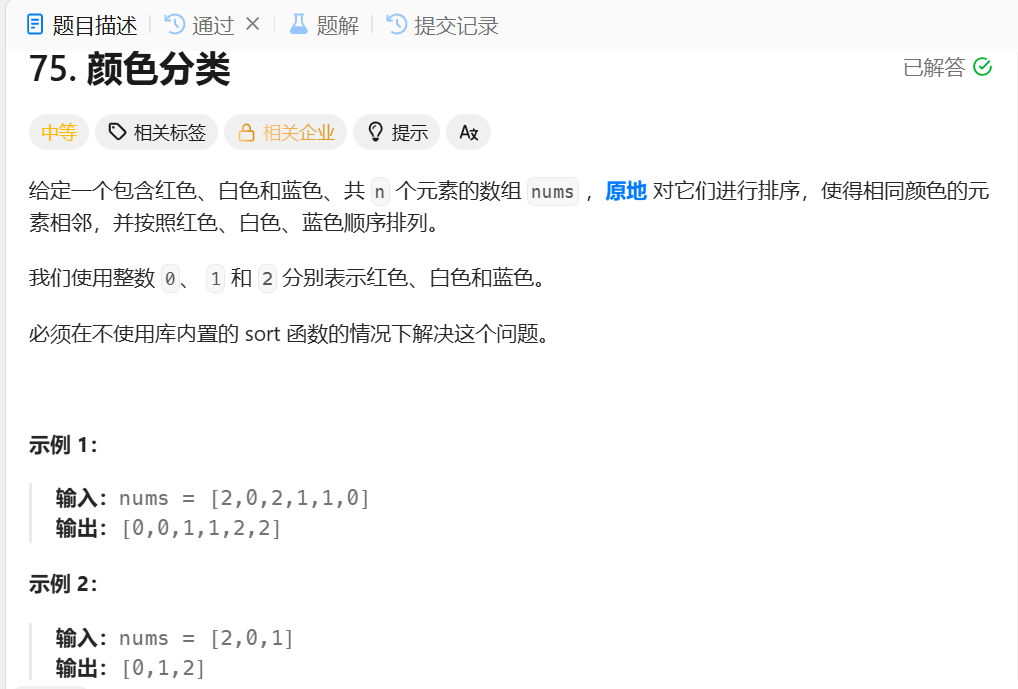
2.解题思路

2.1sortColors01 函数解析

核心思路：分两轮遍历，先把所有 0 移到数组前面，再把所有 1 移到 0 后面（剩下的自然是 2），本质是两次 “冒泡” 式的交换。

void sortColors01(vector<int>& nums) {size_t cur = -1, i = 0;// 第一轮：把所有 0 放到数组前面while (i < nums.size()) {if (nums[i] == 0) swap(nums[++cur], nums[i]);++i;}// 第二轮：把所有 1 放到 0 的后面i = 0; while (i < nums.size()) {if (nums[i] == 1) swap(nums[++cur], nums[i]);++i;}
}

1. 第一轮遍历（处理 0）：

   • cur 初始为 -1，表示 “已排好的 0 的最后位置”。
   • 遍历数组时，遇到 nums[i] == 0，就把 nums[i] 和 nums[++cur] 交换（++cur 先让 cur 指向待交换的位置，再交换），相当于把 0 逐步 “挤” 到数组前面。
   • 比如输入 [2,0,2,1,1,0]，第一轮结束后，cur 会停在最后一个 0 的位置，数组变成 [0,0,2,1,1,2]。

2. 第二轮遍历（处理 1）：

   • 重置 i = 0，cur 延续第一轮的位置（此时指向最后一个 0）。
   • 遍历数组时，遇到 nums[i] == 1，同样用 swap(nums[++cur], nums[i]) 把 1 移到 0 的后面。
   • 第二轮结束后，1 全部排到 0 之后，剩下的 2 自然就在最后，数组最终变为 [0,0,1,1,2,2]。

缺点：需要遍历数组两次，效率不如一次遍历的算法（如 sortColors02）。

2.2sortColors02 函数解析

核心思路：三指针法（一次遍历），用 left 标记 0 的右边界，right 标记 2 的左边界，i 遍历数组，根据 nums[i] 的值与 0/2 交换，逐步收缩边界。

void sortColors02(vector<int>& nums) {size_t left = -1, right = nums.size(), i = 0;while (i < right) { if (nums[i] == 0) swap(nums[++left], nums[i++]);else if (nums[i] == 1) i++; else if (nums[i] == 2) swap(nums[--right], nums[i]); }
}

结合图片

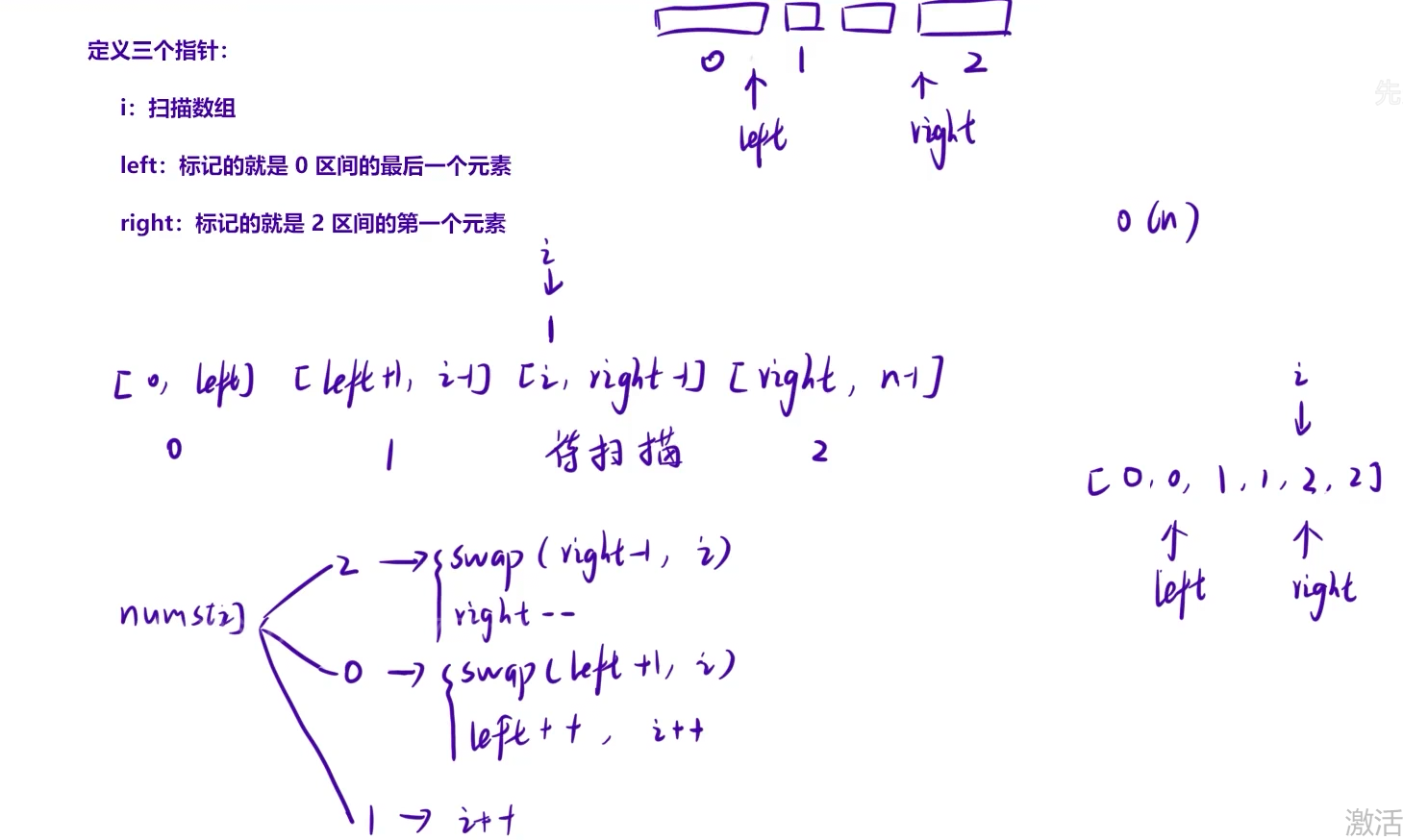
1. 指针含义：

   • left：初始 -1，表示 “已排好的 0 的最后位置”（left + 1 是下一个放 0 的位置）。
   • right：初始 nums.size()，表示 “已排好的 2 的最前位置”（right - 1 是前一个放 2 的位置）。
   • i：遍历指针，负责扫描数组，处理每个元素。

2. 分支逻辑：

   • nums[i] == 0：
     • 交换 nums[++left] 和 nums[i]：把 0 放到 left 的下一个位置，同时 i++ 继续遍历（因为交换后 nums[i] 是之前 nums[++left] 的值，已经处理过）。
   • nums[i] == 1：直接 i++，1 本身就在 “中间区域”，无需交换。
   • nums[i] == 2：
     • 交换 nums[--right] 和 nums[i]：把 2 放到 right 的前一个位置，但不执行 i++（因为交换后 nums[i] 是之前 nums[--right] 的值，可能是 0/1/2，需要重新判断）。

优点：只需遍历数组一次，时间复杂度 O(n)，效率更高，是本题的经典最优解法。

2.3两种方法对比

维度	sortColors01	sortColors02
遍历次数	两次遍历	一次遍历
时间复杂度	O(2n)（等价 O(n)，但常数更大）	O(n)
实现思路	分两轮 “整理” 0 和 1	三指针一次遍历，同时处理 0、1、2
经典性	基础思路	本题最优解法（荷兰国旗问题经典解）

总的来说，sortColors01 是分步处理（先管 0，再管 1），而 sortColors02 是一次遍历 + 三指针，更高效、更贴近 “荷兰国旗问题” 经典解法，实际刷题/面试中优先掌握 sortColors02 的思路。

四.合并两个有序数组

1.题目

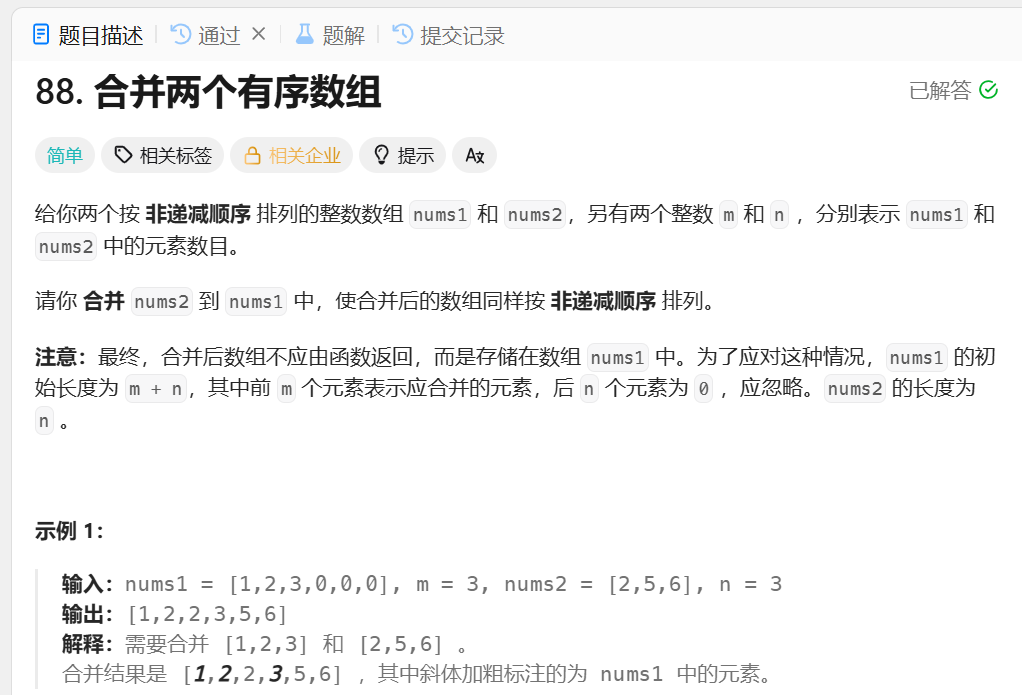
2.解题思路

2.1 题目核心要求

• 输入：两个非递减有序数组 nums1（长度 m + n，前 m 个有效，后 n 个占位 0）、nums2（长度 n）。
• 输出：合并 nums2 到 nums1，最终 nums1 仍非递减有序，且不返回新数组，直接修改 nums1。

2.2 两类解法思路（对应归并排序 “合并阶段” 经典逻辑）

解法一：利用辅助数组（归并排序核心思路）

核心逻辑：

1. 开一个辅助数组，长度 m + n，用来临时存储合并结果。
2. 用 cur1 遍历 nums1 前 m 个元素，cur2 遍历 nums2，cur 遍历辅助数组：
   • 比较 nums1[cur1] 和 nums2[cur2]，把较小值放到辅助数组，对应指针后移。
   • 某个数组遍历完，把另一个数组剩余元素直接 “搬” 到辅助数组。
3. 最后把辅助数组的结果拷贝回 nums1，完成合并。
   

对应图片示例（以 nums1 = [1,2,3,0,0,0], m=3；nums2 = [2,5,6], n=3 为例）：

• 辅助数组初始为空，cur1 指向 nums1[0]，cur2 指向 nums2[0]。
• 比较 1（nums1[0]）和 2（nums2[0]）→ 选 1 放入辅助数组，cur1++。
• 比较 2（nums1[1]）和 2（nums2[0]）→ 选 2 放入辅助数组，cur1++/cur2++。
• 持续此过程，最终辅助数组是 [1,2,2,3,5,6]，再拷贝回 nums1。

参考代码：

void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {vector<int> temp(m + n); // 辅助数组int cur1 = 0, cur2 = 0, cur = 0;while (cur1 < m && cur2 < n) {if (nums1[cur1] < nums2[cur2]) {temp[cur++] = nums1[cur1++];} else {temp[cur++] = nums2[cur2++];}}// 处理剩余元素while (cur1 < m) temp[cur++] = nums1[cur1++];while (cur2 < n) temp[cur++] = nums2[cur2++];// 拷贝回 nums1for (int i = 0; i < m + n; i++) {nums1[i] = temp[i];}
}

特点：

• 优点：逻辑直观，是归并排序 “合并两个有序数组” 的标准步骤，理解后能打通归并排序核心逻辑。
• 缺点：需要额外 O(m + n) 空间（辅助数组）。

解法二：原地合并（本题最优解，利用 nums1 后面的 0 占位）

核心逻辑：
利用 nums1 后面 n 个 0 的 “空闲位置”，从后往前遍历（避免正向遍历覆盖有效元素）：

• cur1 指向 nums1 有效元素末尾（m - 1 位置），cur2 指向 nums2 末尾（n - 1 位置），cur 指向 nums1 最终末尾（m + n - 1 位置）。
• 比较 nums1[cur1] 和 nums2[cur2]，把较大值放到 nums1[cur]，对应指针前移，cur 前移。
• 某个数组遍历完，剩下的元素已经在 nums1 里（或直接 “搬” 完 nums2 剩余元素）。

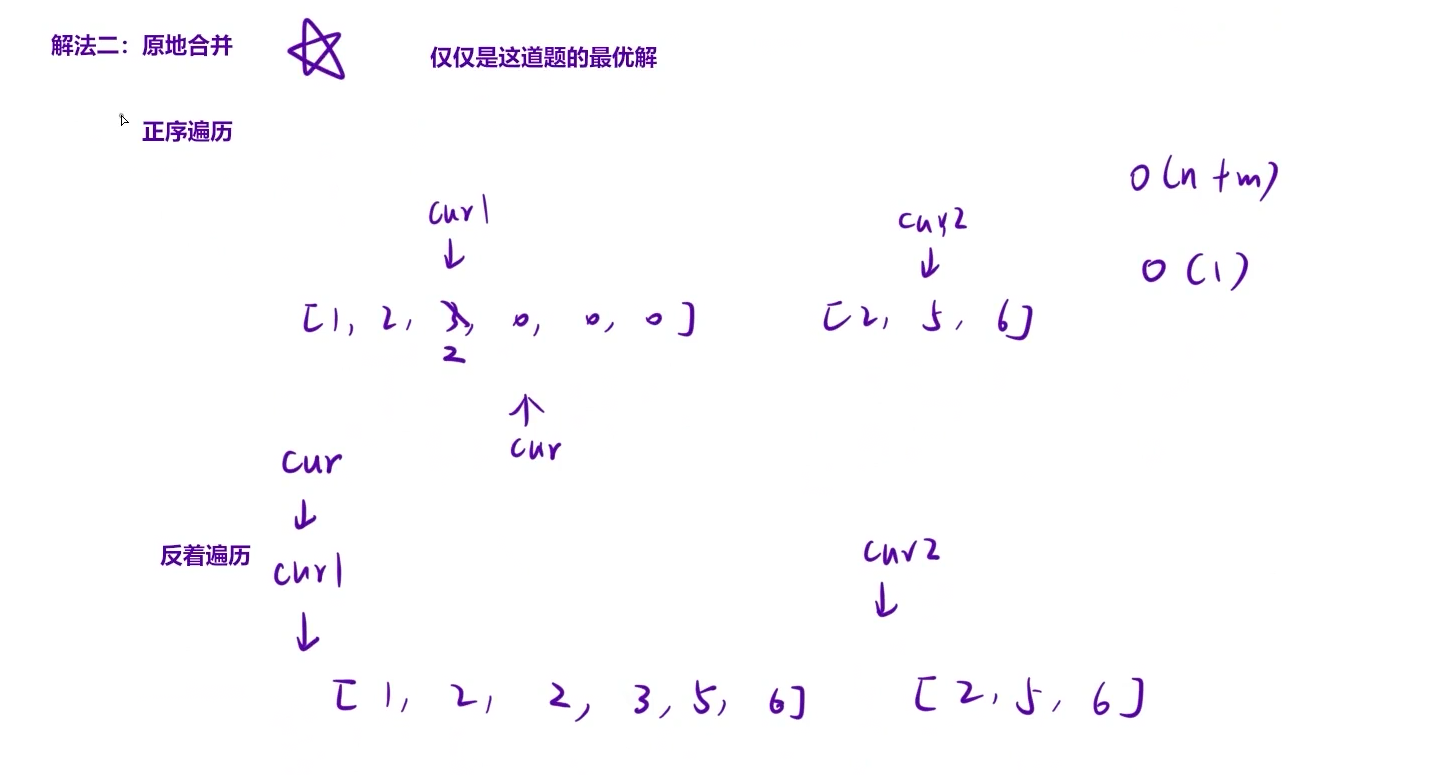
对应图片示例（同样用 nums1 = [1,2,3,0,0,0], m=3；nums2 = [2,5,6], n=3 为例）：

• 初始：cur1 = 2（nums1[2] = 3），cur2 = 2（nums2[2] = 6），cur = 5（nums1[5]）。
• 比较 3 和 6 → 选 6 放到 nums1[5]，cur2--，cur--。
• 比较 3 和 5 → 选 5 放到 nums1[4]，cur2--，cur--。
• 持续此过程，最终 nums1 变成 [1,2,2,3,5,6]。

参考代码：

void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {int cur1 = m - 1, cur2 = n - 1;int cur = m + n - 1;while (cur1 >= 0 && cur2 >= 0) {if (nums1[cur1] > nums2[cur2]) {nums1[cur--] = nums1[cur1--];} else {nums1[cur--] = nums2[cur2--];}}// nums2 可能还有剩余（nums1 已经处理完时），直接搬过去while (cur2 >= 0) {nums1[cur--] = nums2[cur2--];}
}

特点：

• 优点：无需额外空间（O(1) 空间复杂度），利用题目中 nums1 末尾的 0 占位，效率更高，是本题的最优解法。
• 缺点：逻辑是 “从后往前”，需要理解指针反向遍历的思路，和归并排序正向辅助数组思路互补。

2.3 额外补充：“暴力合并 + 排序”

代码逻辑是 “暴力合并 + 排序”，虽然能解决问题，但效率很低（不推荐实际用）：

void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {if (nums2.empty()) return;size_t i = m - 1; for (auto& e : nums2) {nums1[++i] = e; // 把 nums2 元素放到 nums1 后面的 0 里}sort(nums1.begin(), nums1.end()); // 直接排序，时间复杂度 O((m+n)log(m+n))
}

问题：

• 题目要求利用 “两个数组已经有序” 的条件优化，但这段代码直接 sort，没利用有序性，效率比前面两种思路差（尤其数据量大时）。
• 仅适合面试中 “快速写一个能跑的代码”，不是本题考察的核心算法逻辑（归并合并思路）。

2.4 总结（两类解法对比 + 选择建议）

解法	空间复杂度	时间复杂度	核心思路	适用场景
辅助数组（解法一）	O(m + n)	O(m + n)	正向双指针，依赖辅助数组存储	归并排序合并阶段（通用场景）
原地合并（解法二）	O(1)	O(m + n)	反向双指针，利用空闲位置	本题最优解（空间敏感场景）
暴力合并 + 排序	O(1)	O((m+n)log(m+n))	无视有序性，暴力排序	仅临时调试，不推荐实际用

实际刷题/面试中：

• 若考 “归并排序原理”，优先用辅助数组解法（理解归并核心）；
• 若题目明确 “原地合并” 要求（如本题），必须用反向双指针的原地解法；
• 暴力排序写法别在面试正经场合用，会暴露没理解题目 “有序数组合并” 的优化点 。

理清 “合并两个有序数组” 的不同思路，核心是理解 辅助数组正向合并 和 原地反向双指针 的逻辑差异。