当前位置：首页 > news >正文

A Large Scale Synthetic Graph Dataset Generation Framework的学习笔记

news 2025/8/24 13:49:07

文章的简介

作者提出了一个可扩展的合成图生成框架，能够从真实图中学习结构和特征分布，并生成任意规模的图数据集，支持：

节点和边的结构生成
节点和边的特征生成
特征与结构的对齐（Aligner）

它区别于GraphWorld完全自定义参数生成具有各种统计属性的“fake graph”，也不同于传统的图数据集OGB完全取之于真实世界。

文中涉及的一些公式，下面是我对它的理解

图结构生成

目的与动机

目标是生成一个结构上与原始图相似的图结构（即邻接矩阵）。
为了支持生成亿万边规模的图，采用了模型驱动的生成方法，而非深度学习式逐点生成。
核心方法是基于Stochastic Kronecker Graph (SKG) 的思想，是对 R-MAT 的一种泛化。

问题定义

输入图定义为：
$G = (S, F_V, F_E)$
其中

$S = (V, E)$ ：图的结构（节点和边）
$F_V$ ：节点特征矩阵
$F_E$ ：边特征矩阵

目标是学习一个概率分布 $ρ(G)\rho(G)$ ，从中采样生成新图 $G^∼pmodel(G)\hat G \sim p_{model}(G)$ 。

Kronecker图生成机制 / R-MAT（Recursive MATrix）

使用一个基础概率矩阵 $θs=[abcd],a+b+c+d=1\theta_s = \begin{bmatrix} a & b \\ c & d \end{bmatrix},a+b+c+d=1$ ，通过Kronecker乘法（克罗内克积）生成一个规模为 $n=2^m$ 个节点的随机图（通常为有向图），边数为 $E$ ，同时能产生真实网络常见的“幂律度分布、社区/核心-边缘结构”等特征。
支持生成非对称、非方阵邻接矩阵，适用于异构图（如 K-partite 图）。
对于 K-partite 图，邻接矩阵是一个块矩阵，每个块表示不同类型节点之间的连接。

其中最关键的是 $θs\theta_s$ 概率矩阵，它决定“每次二分递归时往哪一个象限走”的偏好。

节点编号与二进制

每个图有 $n=2^m$ 个节点。给每一个节点一个m位二进制编号(0到 $2^m-1$ )。
一条边 $(u, v)$ 对应到邻接矩阵里的一格（第 $u$ 行第 $v$ 列）。R-MAT 会通过递归选择象限的方式，逐步确定这格的位置，也就逐位确定 $u$ 和 $v$ 的二进制位。

生成一条边：从开始到结束的 4 步

我们生成一条边时，从整块 $2m×2m2^m \times 2^m$ ，重复 $m$ 次“选象限”的动作

从整块开始（还不知道源/目标的任何一位）。
一次递归划分：把当前块分成四个象限
- 左上（Top-Left, TL）概率 $a$
- 右上（TR）概率 $b$
- 左下（BL）概率 $c$
- 右下（BR）概率 $d$
落到某象限后，该象限就相当于“把源或目标的最高未确定那一位写成 0/1”：
- 选到上半（TL 或 TR）：源端(行)这一位是 0；选到下半（BL 或 BR）：源端这一位是 1。
- 选到左半（TL 或 BL）：目标端（列）这一位是 0；选到右半（TR 或 BR）：目标端这一位是 1。
- 于是，这一次递归需要同时确定了 $u$ 的一位和 $v$ 的一位。
缩小到该象限，继续做下一次递归（再次四分、再次按 $a, b, c, d$ 选择），直到坐满 $m$ 次。此时两端的 $m$ 位都定了，得到了一个具体的 $(u, v)$ ，这样就确立了一条边。

一条边的“落点”是 $m$ 次独立象限选择的产物。重复上面流程 $E$ 次，即可得到 $E$ 条边。（可允许多重边/自环，具体看实现是否去重或拒绝自环）。

和 3.2 节里推导 $c^kout\hat c_k^{out}$ 对齐

内部的二项分布概率质量函数

其实就是把“选象限”的四个概率合并成对行与列的边际：

源端（行）选择“上半/下半”的概率分别是
$Pr(源=上)=a+b\triangleq p, Pr(源=下)=c+d\triangleq 1- p.$
目标端（列）选择“左半/右半”的概率分别是
$Pr(目标=左)=a+c\triangleq 1, Pr(目标=右)=b+d\triangleq 1- q.$
于是，在每一层递归：
源端这一位是 0（上半）的概率为 $p$ ，是 1（下半）的概率为 $1 - p$ ；
目标端这一位是 0（左半）的概率为 $q$ ，是 1（右半）的概率为 $1 - q$ 。

因为每层都是独立同分布，这就带来一个关键结论：
某个固定源节点 $u$ （它的二进制里有 $i$ 个 1）在一次“抽一条边”里被选为源的单次概率是 $r_i=p^{m-i}(1-p)^i$
只与“1 的个数 i”有关，不依赖具体哪些位是 1。这样“有 i 个 1 的节点”一共有 $(mi)\binom{m}{i}$ 个，而且它们的单次概率都相同——这正是 3.2 节里分层求和内部的二项分布的概率公式的来源。

一个具体的小例子（m=2）

设 $m = 2 \Rightarrow n = 4$ 个节点，节点编号 00,01,10,11。
设 $a = 0.45, b = 0.15, c = 0.15, d = 0.25$ （满足和为 1）。
- $p = a + b = 0.60 ； q = a + c = 0.60$ 。
生成一条边需要 2 次象限选择。比如两次都抽到 TR（右上）：
- 第 1 次 TR：源位=0（上），目标位=1（右）；
- 第 2 次 TR：源位=0（上），目标位=1（右）；
- 得到 $(源节点 u = 00, 目标节点 v = 11)$ 。这条边的路径概率是 $b \times b$ 。

反过来想，假如给定了一个源节点（比如 $u = 10$ ，二进制有 $i = 1$ 个 1），则让它作为一条边的源的单次概率是 $r_1=p^{m-i}(1-p)^i=0.6^1 * 0.4^1=0.24$ 。

外部的二项分布概率质量函数

文中提到先生成与输入图等大小的图（这里假设要生成的图是无向节点异构边同构图），即生成邻接矩阵 $A^\hat A$ 的大小是 $\times m$ ，生成图 $G^\hat G$ 节点数量是 $n + m$ （因为异构这里 $n, m$ 分别表示两种类型），而后在拓展。其中用一个二维概率分布矩阵 $θ\theta$ 来描述在生成图中某个节点对之间存在边的概率，即 $A^∼θ\hat A \sim \theta$ 。
$θ=θS⊗min⁡(m,n)⊗θH⊗max⁡(0,n−m)⊗θV⊗max⁡(0,m−n)\theta = \theta_S^{\otimes \min(m,n)} \otimes \theta_H^{\otimes \max(0,n-m)} \otimes \theta_V^{\otimes \max(0,m-n)}$
这个矩阵不是直接给定的，而是通过多个 Kronecker 积构造出来的(参看上一节)，以便模拟真实图的结构特性（如幂律分布、社区结构等）。其中：
$θS=[abcd],θH=[q1−q],θV=[p1−p]\theta_S = \begin{bmatrix} a & b \\ c & d \end{bmatrix}, \quad \theta_H = \begin{bmatrix} q & 1 - q \end{bmatrix}, \quad \theta_V = \begin{bmatrix} p \\ 1 - p \end{bmatrix}$

$\lceil \log_2 M \rceil, \quad n = \lceil \log_2 N \rceil$
这里是因为R-MAT 是在一个 $2m(行数)×2n（列数）2^m(行数) \times 2^n（列数）$ 的邻接矩阵上生成边。R-MAT 的二分递归必须工作在 2 的幂次规模，但是现实中我们想要的节点数 $M, N$ 不一定正好是 2 的整数次幂。所以要取上整，保证覆盖，然后再裁掉多余的。
$\quad q = a + c$
其中 $θH,θV\theta_H, \theta_V$ 分别表示用于扩展 Kronecker 种子矩阵 $θS\theta_S$ 的两个边缘矩阵，它们分别控制图在横向（列）和纵向（行）的扩展方式。它们的设计是为了生成非方形的邻接矩阵，从而支持异构图或 $K$ -部图的生成。这里用于表示在 $n > m$ 时用 $θH\theta_H$ 拓展，相等时不拓展，否则用 $θV\theta_V$ 拓展。（KDD的发表版里公式表述有错，请注意）。
为了仿照输入图的属性， $θS\theta_S$ 的定义比较讲究，定义了目标函数
$J(θS)∝∑kin=0kmaxin(ckin−c^kin)2+∑kout=0kmaxout(ckout−c^kout)2 J(\theta_S) \propto \sum_{k^{\text{in}}=0}^{k_{\text{max}}^{\text{in}}} \left( c_k^{\text{in}} - \hat{c}_k^{\text{in}} \right)^2 + \sum_{k^{\text{out}}=0}^{k_{\text{max}}^{\text{out}}} \left( c_k^{\text{out}} - \hat{c}_k^{\text{out}} \right)^2$
其中 $c_k^{in}$ 表示输入图 $G$ 中入度为 $k$ 的节点数量， $c^kin\hat c_k^{in}$ 则是估计的生成图 $G^\hat G$ 中入度为 $k$ 的节点数量，同理可推别的。其中 $c^kout\hat c_k^{out}$ 定义为：
$c^kout=(Ek)∑i=0m(mi)[pm−i(1−p)i]k⋅[1−(pm−i(1−p)i)]E−k\hat{c}_k^{\text{out}} = \binom{E}{k} \sum_{i=0}^{m} \binom{m}{i} \left[ p^{m-i}(1-p)^i \right]^k \cdot \left[ 1 - \left( p^{m-i}(1-p)^i \right) \right]^{E-k}$
其外部也是一个二项分布概率质量函数，这里

把“抽一条边、源端击中某节点”看作一次伯努利试验，成功概率取决于该节点所属的“ $i$ 类”概率 $r_i$ 。
抽 E 条边（独立同分布）→ 该节点的出度 $Binomial(E,r_i)$ ；
则出度为 $k$ 的概率就是
$\binom{E}{k}r_i^k(1-r_i)^{E-k}$
每个 $i$ 类都有 $(mi)\binom{m}{i}$ 个节点，对所有的 $i$ 汇总，就得到“出度为 $k$ 的节点数的期望” $c^kout\hat c_k^{out}$

整个流程常见实现细节/变体

去重与自环：有的实现允许多重边/自环（生成更快）；有的会在采样后拒绝自环或去重，会稍增耗时。
- 多重边 (multiple edges)：在抽 $E$ 条边时，因为每条边都是独立随机的，所以可能多次落在同一个位置 $(u, v)$ 。这就产生了相同的边重复出现。
  比如节点 00 → 11 这条边可能被抽中 5 次，那么结果图里就有 5 条相同的边。
- 自环 (self-loop)：边的源端和目标端是同一个节点，即 $(u, u)$ 。
  比如 10 → 10，这种边在很多场景下不是我们想要的。

(a) 允许多重边/自环
做法：生成多少就记多少，不做过滤。
优点：实现简单，速度最快（每次递归选象限 → 写下结果 → 下一条）。
结果：图可能会有重复边，也可能有节点自己指向自己。
常见用途：做大规模随机基准测试时（比如只关心度分布的大体形状），允许多重边/自环没关系。
(b) 去重/去自环
去自环：如果生成的边是 $(u, u)$ ，就丢弃，重新采样。
去重：如果生成的边在集合里已经有了，就丢弃，重新采样。
优点：得到的图是“简单图”（simple graph），即没有重复边和自环。很多图算法理论默认输入是简单图。
缺点：需要检查和重采样，带来额外的开销。尤其当E接近 $n^2$ （非常稠密）时，重复率会很高，代价可能很大。

噪声/抖动：为避免棋盘状伪影，常在每层对 $(a, b, c, d)$ 进行轻微扰动或随机打乱节点标签（label permutation）。

R-MAT每次递归选择象限时都用同一个固定概率矩阵,重复 $m$ 次 → 节点编号和边的分布跟二进制位高度相关。结果是：
1.节点的出度/入度不光依赖概率，还依赖它二进制编号的“模式”（多少个 1，多少个 0）。
2.邻接矩阵可视化时会出现一种棋盘格（checkerboard）样的规律性伪影：某些大块区域特别稠密，某些大块特别稀疏，看起来像分层的棋盘格，而不是自然网络里平滑的社区/局部密集结构。
这就是所谓的 R-MAT 伪影 (artifacts)。
为了缓解这种人为模式，人们引入随机扰动：
(a) 概率扰动（noise / jitter）
在每一层递归时，不直接用固定的 $(a, b, c, d)$ ，而是加上一点小的随机噪声。例如 $a′=a+ϵa,b′=b+ϵb,c′=c+ϵc,d′=d+ϵd,a'=a+\epsilon_a, b'=b+\epsilon_b, c'=c+\epsilon_c, d'=d+\epsilon_d,$
然后再正规化保证它们加起来为 1。这样，每一层递归的选择概率都会有细微差别，避免边总是严格落在固定模式的位置。
(b) 标签随机化（label permutation）
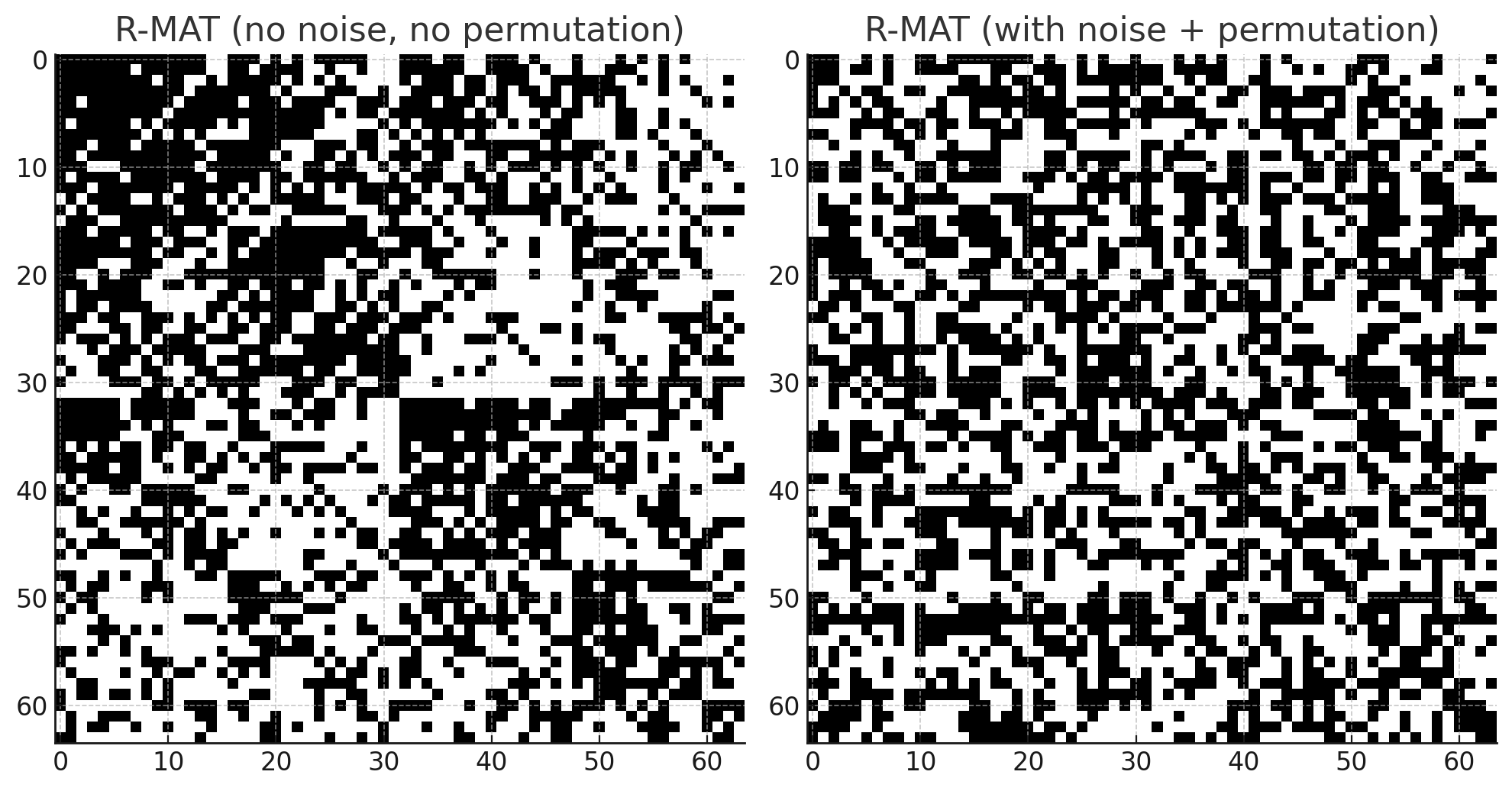
在生成边之后，把节点的编号随机打乱一次（或者在生成过程中，间歇性打乱节点标签）。本质上就是“洗掉”二进制编号和度分布之间的强耦合关系，让边的分布更接近自然网络。示意图大概长这样

无向图：生成后把 $(u, v)$ 当作无向边，或只保留 $u < v$ 的一半。
关系到 Kronecker/SKG：R-MAT 与后来的 Stochastic Kronecker Graph (SKG) 在思想上是对应的（一边“递归抽象限”，一边“Kronecker 乘生成矩阵”），参数可相互映射。