算法训练营day60 图论⑩ Bellman_ford 队列优化算法、判断负权回路、单源有限最短路（修改后版本）

        增加对最短路径的优化算法、负权回路、单源有限最短的讲解

Bellman_ford 队列优化算法

--------------------------------------------------------------------------------

        8.24更新：该算法是针对带负值的最短路径的优化算法，核心通过队列来实现，代码中visit数组来标记在队列中的元素，以防重复入队，每次循环一个节点的出度，即自该节点出发的边，模拟过程中队列判断n次（均由队列实现，具体次数无循环语句要求）

--------------------------------------------------------------------------------

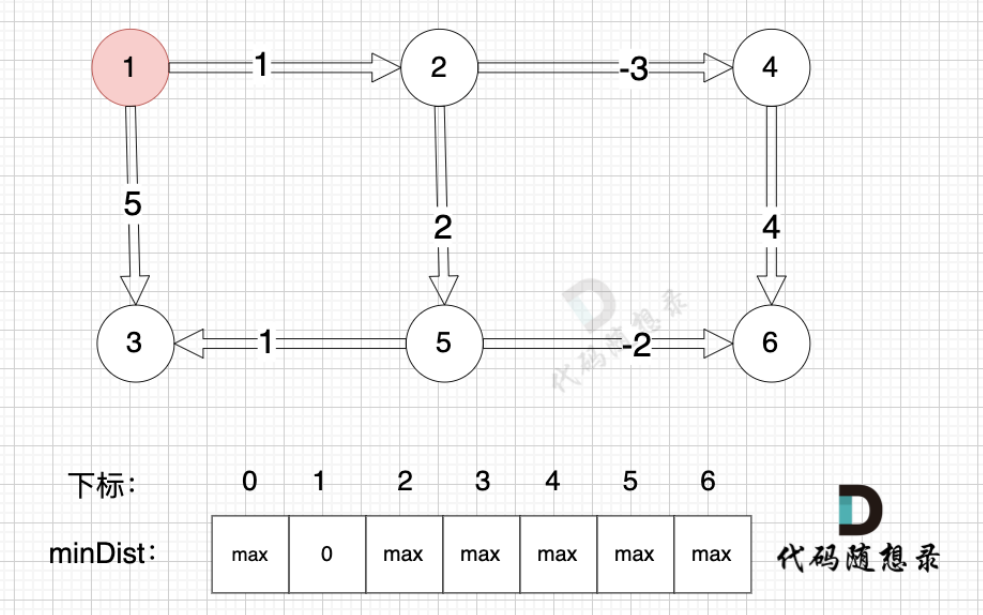
        我们之前的松弛算法，是对所有边进行松弛，真正有效的松弛，只有松弛 边（节点1->节点2） 和 边（节点1->节点3）。而松弛 边（节点4->节点6），边（节点5->节点3）等等 都是无效的操作，因为 节点4 和 节点 5 都是没有被计算过的节点。所以 Bellman_ford 算法 每次都是对所有边进行松弛，其实是多做了一些无用功。

        只需要对 上一次松弛的时候更新过的节点作为出发节点所连接的边 进行松弛就够了。

        基于以上思路，如何记录 上次松弛的时候更新过的节点呢？用队列来记录。简单理解就是每次mindist数组中被更新过的位置就是需要入栈的元素，然后栈顶元素进行松弛操作出栈，同时被修改的元素入栈，最后完成所有的循环（其实用栈也行，对元素顺序没有要求）

效率分析

        如果图越稠密，则 SPFA的效率越接近与 Bellman_ford。反之，图越稀疏，SPFA的效率就越高。一般来说，SPFA 的时间复杂度为 O(K * N) K 为不定值，因为 节点需要计入几次队列取决于 图的稠密度。

        SPFA（队列优化版Bellman_ford） 在理论上 时间复杂度更胜一筹，但实际上，也要看图的稠密程度，如果 图很大且非常稠密的情况下，虽然 SPFA的时间复杂度接近Bellman_ford，但实际时间消耗 可能是 SPFA耗时更多。

代码实现

        最根本的理解，我们这个代码是以边为主的，注意本题没有 负权回路 。

import collectionsdef main():n, m = map(int, input().strip().split())edges = [[] for _ in range(n + 1)]for _ in range(m):src, dest, weight = map(int, input().strip().split())edges[src].append([dest, weight])minDist = [float("inf")] * (n + 1)minDist[1] = 0que = collections.deque([1])visited = [False] * (n + 1)visited[1] = Truewhile que:cur = que.popleft()visited[cur] = Falsefor dest, weight in edges[cur]:if minDist[cur] != float("inf") and minDist[cur] + weight < minDist[dest]:minDist[dest] = minDist[cur] + weightif visited[dest] == False:que.append(dest)visited[dest] = Trueif minDist[-1] == float("inf"):return "unconnected"return minDist[-1]if __name__ == "__main__":print(main())

Bellman_ford 判断负权回路

--------------------------------------------------------------------------------

        8.24更新：核心思路就是多松弛一次，看mindist数组有没有变化（负权回路会导致mindist数组变化)，优化算法中的判断负权回路：如果节点加入队列的次数 超过了 n-1次 ，那么该图就一定有负权回路。

        怎么判断数组有没有变化？还是一样的逻辑，看有没有变小即可

        最后一点，普通方法把边都遍历一遍这种，没有什么特别的说法，直接多松弛一次即可，但是优化算法中的负权回路，因为引入了队列，所以一定记得对于队列内已经进入的元素不要重复进入，（这个是上一题目中的基本内容了），这里的拓展我认为有一些主动写错来纠偏的部分了，反而可能更加容易引起误导

--------------------------------------------------------------------------------

        本题是要我们判断 负权回路，也就是图中出现环且环上的边总权值为负数。如果在这样的图中求最短路的话， 就会在这个环里无限循环 （也是负数+负数 只会越来越小），无法求出最短路径。

        在上期博客中，bellman_ford 算法的核心就是一句话：对 所有边 进行 n-1 次松弛。 在没有负权回路的图中，松弛 n 次以上 ，结果不会有变化。但本题有 负权回路，如果松弛 n 次，结果就会有变化了，因为 有负权回路 就是可以无限最短路径（一直绕圈，就可以一直得到无限小的最短距离）。

        那么解决本题的 核心思路，就是在 n-1 次松弛 的基础上，再多松弛一次，看minDist数组 是否发生变化。

Bellman-Ford方法

import sysdef main():input = sys.stdin.readdata = input().split()index = 0n = int(data[index])index += 1m = int(data[index])index += 1grid = []for i in range(m):p1 = int(data[index])index += 1p2 = int(data[index])index += 1val = int(data[index])index += 1# p1 指向 p2，权值为 valgrid.append([p1, p2, val])start = 1  # 起点end = n    # 终点minDist = [float('inf')] * (n + 1)minDist[start] = 0flag = Falsefor i in range(1, n + 1):  # 这里我们松弛n次，最后一次判断负权回路for side in grid:from_node = side[0]to = side[1]price = side[2]if i < n:if minDist[from_node] != float('inf') and minDist[to] > minDist[from_node] + price:minDist[to] = minDist[from_node] + priceelse:  # 多加一次松弛判断负权回路if minDist[from_node] != float('inf') and minDist[to] > minDist[from_node] + price:flag = Trueif flag:print("circle")elif minDist[end] == float('inf'):print("unconnected")else:print(minDist[end])if __name__ == "__main__":main()

SPFA方法

        这里涉及的问题是节点重复入队，导致本应n-1次结束的过程，没有按时结束，我们需要记录哪些节点已经出队列了，哪些节点在队列里面，对于还在队列内部的节点不要重复入队

from collections import deque
from math import infdef main():n, m = [int(i) for i in input().split()]graph = [[] for _ in range(n+1)]min_dist = [inf for _ in range(n+1)]count = [0 for _ in range(n+1)]  # 记录节点加入队列的次数for _ in range(m):s, t, v = [int(i) for i in input().split()]graph[s].append([t, v])min_dist[1] = 0  # 初始化count[1] = 1d = deque([1])flag = Falsewhile d:  # 主循环cur_node = d.popleft()for next_node, val in graph[cur_node]:if min_dist[next_node] > min_dist[cur_node] + val:min_dist[next_node] = min_dist[cur_node] + valcount[next_node] += 1if next_node not in d: # 二刷的时候再好好理解d.append(next_node)if count[next_node] == n:  # 如果某个点松弛了n次，说明有负回路flag = Trueif flag:breakif flag:print("circle")else:if min_dist[-1] == inf:print("unconnected")else:print(min_dist[-1])if __name__ == "__main__":main()

Bellman_ford 单源有限最短路

--------------------------------------------------------------------------------

        8.24更新：节点数量为n，起点到终点，最多是 n-1 条边相连。 那么对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。这个n - 1要理解，这也是松弛的最基本逻辑，就不多讲了。（如果对以上讲解看不懂，建议详看 kama94.城市间货物运输I ）

        但是仅有这个理解是不够的，这里我还是要吐槽一下，可能是我没看视频，我认为这道题目的文字版解析说的不好，可能是我没有理解到位，我认为出现问题的本质是：在修改过程中修改了已经遍历过的节点的值，地基变了，自然下一轮中所有的值都会修改，引起这个问题的本质是：路径中存在负权回路，而不是文字版讲解中说的：基于了本次松弛的 minDist数值，而不是上一次 松弛时候minDist的数值。这个讲解歪曲了这个问题的本质，反而让全文显得很啰嗦并且具有误导性。

        解决这个问题的方法是：解决负权环路的判断，如何解决？环路最少有两条边，隔开这两条边，也就是文字版解析中给出的解决方法，但是这个是后验的，不可以在开始就把问题归结到这一点上

        最后dijkstra显然是不能用的

--------------------------------------------------------------------------------

        注意题目中描述是 最多经过 k 个城市的条件下，而不是一定经过k个城市，也可以经过的城市数量比k小，但要最短的路径。对于部分路径节点多但是距离短的结果增加了要求

        在 这个系列的第一个题目 中我们讲了：对所有边松弛一次，相当于计算 起点到达 与起点一条边相连的节点 的最短距离。节点数量为n，起点到终点，最多是 n-1 条边相连。 那么对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。本题是最多经过 k 个城市， 那么是 k + 1条边相连的节点。 

Bellman-Ford方法求解单源有限最短路

def main():# 輸入n, m = map(int, input().split())edges = list()for _ in range(m):edges.append(list(map(int, input().split() )))start, end, k = map(int, input().split())min_dist = [float('inf') for _ in range(n + 1)]min_dist[start] = 0# 只能經過k個城市，所以從起始點到中間有(k + 1)個邊連接# 需要鬆弛(k + 1)次for _ in range(k + 1):update = Falsemin_dist_copy = min_dist.copy()for src, desc, w in edges:if (min_dist_copy[src] != float('inf') and min_dist_copy[src] + w < min_dist[desc]):min_dist[desc] = min_dist_copy[src] + wupdate = Trueif not update:break# 輸出if min_dist[end] == float('inf'):print('unreachable')else:print(min_dist[end])if __name__ == "__main__":main()

SPFA方法求解单源有限最短路

from collections import deque
from math import infdef main():n, m = [int(i) for i in input().split()]graph = [[] for _ in range(n+1)]for _ in range(m):v1, v2, val = [int(i) for i in input().split()]graph[v1].append([v2, val])src, dst, k = [int(i) for i in input().split()]min_dist = [inf for _ in range(n+1)]min_dist[src] = 0  # 初始化起点的距离que = deque([src])while k != -1 and que:visited = [False for _ in range(n+1)]  # 用于保证每次松弛时一个节点最多加入队列一次que_size = len(que)temp_dist = min_dist.copy()  # 用于记录上一次遍历的结果for _ in range(que_size):cur_node = que.popleft()for next_node, val in graph[cur_node]:if min_dist[next_node] > temp_dist[cur_node] + val:min_dist[next_node] = temp_dist[cur_node] + valif not visited[next_node]:que.append(next_node)visited[next_node] = Truek -= 1if min_dist[dst] == inf:print("unreachable")else:print(min_dist[dst])if __name__ == "__main__":main()