第十七周-通用量子门与Deutsch-Jozsa算法
目录
摘要
一、协议的量子线圈呈现
二. 量子门的通用性(Universality)
状态距离与操作距离
通用性的定义
通用性的必要条件
常见的通用门集合
效率与Solovay-Kitaev定理
三. 相位反冲(Phase Kickback)
基本设置
四. Deutsch问题
问题描述
经典与量子对比
量子算法步骤
五. Deutsch-Jozsa问题
问题描述
经典与量子对比
量子算法步骤
六、总结
摘要
本文探讨了量子计算的三个核心概念:1)通用量子门集合,通过有限门组合实现任意酉操作,其中{CNOT,H,T}门集合具有通用性;2)相位反冲技术,将函数信息转化为相位变化;3)Deutsch-Jozsa算法,展示了量子计算在函数判定问题上的指数加速优势。研究表明,量子计算通过通用门集合和相位反冲等技术,在特定问题上展现出超越经典计算的潜力。
Abstrac
tThis paper explores three core concepts of quantum computing: 1) Universal quantum gate set, which achieves arbitrary unitary operations through combinations of a finite set of gates, among which the {CNOT, H, T} gate set is universal; 2) Phase kickback technique, which converts function information into phase changes; 3) Deutsch-Jozsa algorithm, demonstrating the exponential speed-up of quantum computing in function determination problems. The study shows that quantum computing, through techniques such as universal gate sets and phase kickback, exhibits potential to surpass classical computation in specific problems.
一、协议的量子线圈呈现
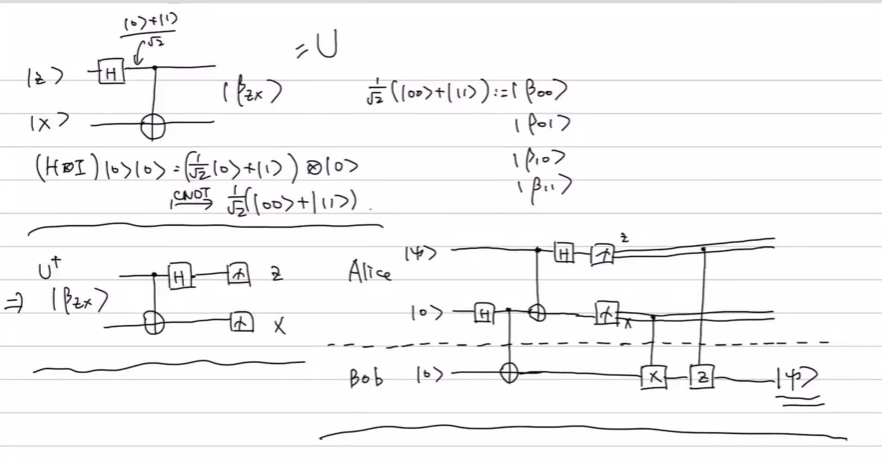
二. 量子门的通用性(Universality)
在量子计算中,我们希望使用有限的量子门集合来实现任意复杂的量子操作,并以此量化计算的复杂性和容错能力。这就涉及到对任意量子态的逼近问题。
状态距离与操作距离
-
状态距离定义为:
∥∣ψ⟩−∣ϕ⟩∥=(⟨ψ∣−⟨ϕ∣)(∣ψ⟩−∣ϕ⟩)∥∣ψ⟩−∣ϕ⟩∥=(⟨ψ∣−⟨ϕ∣)(∣ψ⟩−∣ϕ⟩)

-
操作距离定义为:
E(U,V)=max∣ψ⟩∥U∣ψ⟩−V∣ψ⟩∥E(U,V)=∣ψ⟩max∥U∣ψ⟩−V∣ψ⟩∥
例如,E(X,I)=2E(X,I)=2,因为 X∣−⟩=∣+⟩X∣−⟩=∣+⟩,与 I∣−⟩=∣−⟩I∣−⟩=∣−⟩ 的距离为2。
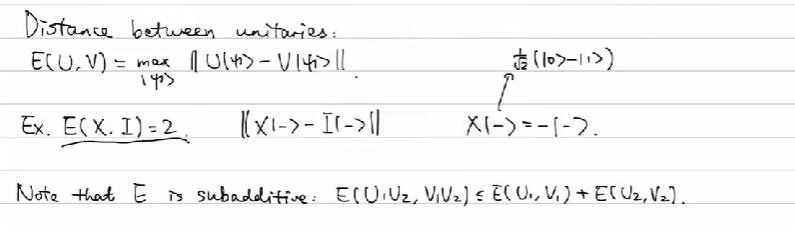
通用性的定义
一个量子门集合是通用的,如果对于任意正整数 nn、任意 nn 量子比特的酉操作 UU 和任意 ϵ>0ϵ>0,都可以从该集合中找到一组门 V1,V2,…,VkV1,V2,…,Vk,使得:
E(U,V1V2⋯Vk)≤ϵE(U,V1V2⋯Vk)≤ϵ
通用性的必要条件
-
必须包含一个纠缠门(如CNOT),能将乘积态转换为纠缠态。
-
对于单量子比特门,必须能实现任意旋转,尤其是非有理数倍 ππ 的旋转。
常见的通用门集合
-
{CNOT, H, T},其中 T=RZ(π4)=(100eiπ/4)T=RZ(4π)=(100eiπ/4)
通过组合 HTHTHTHT 或 THTHTHTH 可以实现无理数角度旋转,从而逼近任意单比特门。

效率与Solovay-Kitaev定理
-
并非所有 nn 量子比特的酉操作都可以用多项式数量的门实现。
-
Solovay-Kitaev定理:对于任意封闭且包含逆操作的通用单比特门集合,任何单比特门都可以用 O(log4(1/ϵ))O(log4(1/ϵ)) 个门逼近到误差 ϵϵ。
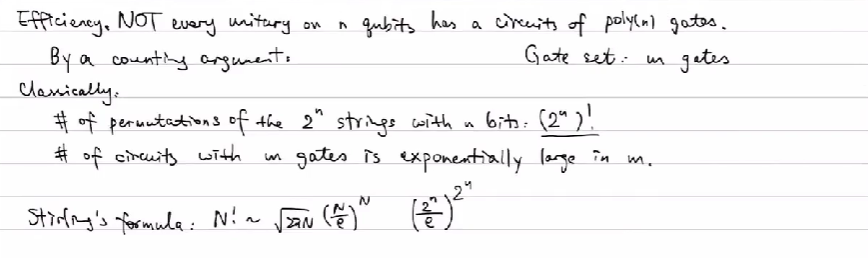

三. 相位反冲(Phase Kickback)
相位反冲是量子算法中一种重要的技术,用于将函数的相位信息“反冲”到前一个寄存器中。
基本设置
考虑一个查询问题:
∣x⟩∣y⟩→∣x⟩∣y⊕f(x)⟩∣x⟩∣y⟩→∣x⟩∣y⊕f(x)⟩
如果我们将第二个寄存器初始化为 ∣−⟩=12(∣0⟩−∣1⟩)∣−⟩=21(∣0⟩−∣1⟩),则:
∣x⟩∣−⟩→(−1)f(x)∣x⟩∣−⟩∣x⟩∣−⟩→(−1)f(x)∣x⟩∣−⟩
函数的取值 f(x)f(x) 以相位的形式出现在第一个寄存器中,这就是相位反冲。
四. Deutsch问题
问题描述
给定一个黑盒函数 f:{0,1}→{0,1}f:{0,1}→{0,1},判断 ff 是常数函数还是平衡函数(即 f(0)⊕f(1)=0f(0)⊕f(1)=0 或 1)。
经典与量子对比
-
经典算法:需要2次查询才能确定。
-
量子算法:仅需1次查询。

量子算法步骤
-
初始状态:∣0⟩∣1⟩∣0⟩∣1⟩
-
对第一个寄存器作用 HH,第二个寄存器也作用 HH 得到 ∣−⟩∣−⟩:
∣0⟩∣1⟩→H⊗H∣+⟩∣−⟩∣0⟩∣1⟩H⊗H∣+⟩∣−⟩ -
作用 UfUf:
∣+⟩∣−⟩→12((−1)f(0)∣0⟩+(−1)f(1)∣1⟩)∣−⟩∣+⟩∣−⟩→21((−1)f(0)∣0⟩+(−1)f(1)∣1⟩)∣−⟩ -
对第一个寄存器再次作用 HH:
-
若 f(0)=f(1)f(0)=f(1),得到 ∣0⟩∣0⟩
-
若 f(0)≠f(1)f(0)=f(1),得到 ∣1⟩∣1⟩
-
测量第一个寄存器即可判断 ff 是常数还是平衡。
五. Deutsch-Jozsa问题
问题描述
给定一个黑盒函数 f:{0,1}n→{0,1}f:{0,1}n→{0,1},已知 ff 要么是常数函数,要么是平衡函数(即一半输入输出0,一半输出1)。要求确定 ff 是哪一种。
经典与量子对比
-
经典确定性算法:最坏情况下需要 2n−1+12n−1+1 次查询。
-
量子算法:仅需1次查询。

量子算法步骤
-
初始状态:∣0⟩⊗n∣1⟩∣0⟩⊗n∣1⟩
-
对所有寄存器作用 HH:
∣0⟩⊗n∣1⟩→H⊗n⊗H∑x∈{0,1}n12n∣x⟩∣−⟩∣0⟩⊗n∣1⟩H⊗n⊗Hx∈{0,1}n∑2n1∣x⟩∣−⟩ -
作用 UfUf:
∑x12n∣x⟩∣−⟩→∑x(−1)f(x)2n∣x⟩∣−⟩x∑2n1∣x⟩∣−⟩→x∑2n(−1)f(x)∣x⟩∣−⟩ -
对前 nn 个寄存器再次作用 H⊗nH⊗n:
∑x(−1)f(x)2n∣x⟩→H⊗n∑yay∣y⟩x∑2n(−1)f(x)∣x⟩H⊗ny∑ay∣y⟩其中:
ay=12n∑x(−1)f(x)+x⋅yay=2n1x∑(−1)f(x)+x⋅y -
测量前 nn 个寄存器:
-
若得到 y=0⋯0y=0⋯0,则 ff 是常数函数;
-
否则,ff 是平衡函数。


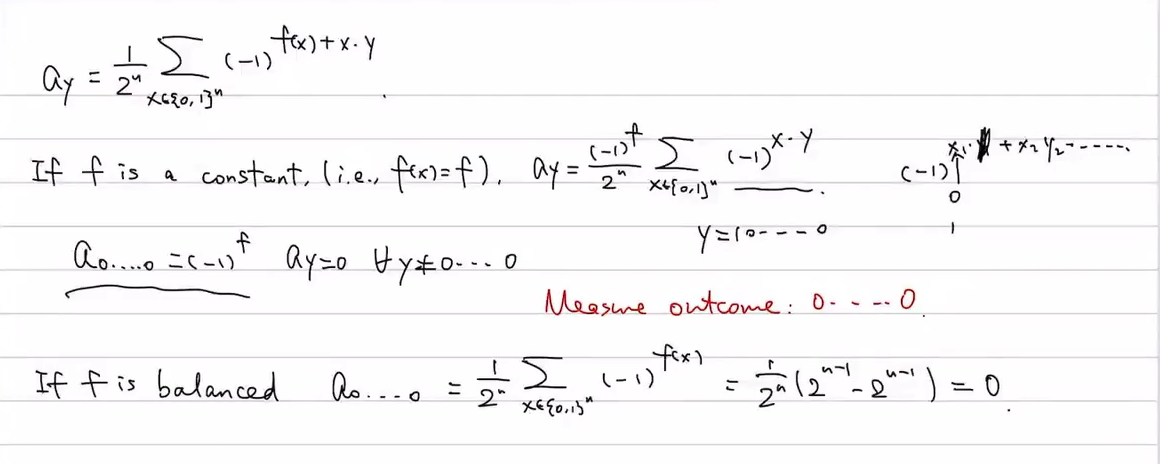

-
六、总结
量子计算之所以强大,首先在于它拥有一套可以搭建任何复杂计算的"基础积木"—这就是量子门的通用性。而相位反冲就像是一个巧妙的戏法,让量子算法能够把关键信息巧妙地传递和转化。这两者结合,孕育出了像Deutsch-Jozsa这样令人惊叹的算法——它解决了一个经典计算机需要检查超过一半可能性才能确定答案的问题,而量子计算机只需要看一眼就能给出确定无疑的答案。虽然用经典的随机抽样方法也能以较高概率猜对结果,但量子计算的魅力就在于它能一击即中,这种在确定性计算上的绝对优势,让我们看到了它解决某些难题的巨大潜力。
