【数据结构】顺序栈的基本操作
目录
一、数据结构定义:顺序栈的存储结构
二、基础操作算法
1. 初始化栈(InitStack)
2. 判断栈空(StackEmpty)
3. 判断栈满(StackFull)
4. 求栈长度(StackLength)
5. 清空栈(ClearStack)
6. 销毁栈(DestroyStack)
7. 入栈(Push)
8. 出栈(Pop)
9. 获取栈顶元素(GetTop)
三、扩展操作算法
1. 栈扩容(ExpandStack)
2. 栈遍历(TraverseStack)
3. 栈复制(CopyStack)
4. 栈比较(CompareStack)
四、典型应用:进制转换(Conversion)
五、顺序栈的基本操作的代码完整实现
(一)C++代码
(二)Python代码
(三)Java代码
六、程序运行结果展示
(一)C++程序运行截图
(二)Python程序运行截图
(三)Java程序运行截图
七、算法整体总结
一、数据结构定义:顺序栈的存储结构
typedef int SElemType; // 栈元素类型(可替换为其他类型,如char、struct等)
typedef struct {SElemType *base; // 栈底指针:指向数组起始位置(固定不变,除非扩容)SElemType *top; // 栈顶指针:指向栈顶元素的**下一个位置**(空栈时与base重合)int stacksize; // 当前栈的最大容量(数组长度)int increment; // 扩容增量:栈满时自动扩容的大小
} SqStack;
设计思想:用动态数组(base指向的连续内存)存储栈元素,通过top与base的差值计算栈中元素数量,通过stacksize限制最大容量,increment支持动态扩容。
二、基础操作算法
1. 初始化栈(InitStack)
void InitStack(SqStack &S, int incr = INCREMENT) {S.base = new SElemType[MAXSIZE]; // 分配初始容量为MAXSIZE的数组if (!S.base) { // 内存分配失败检查cerr << "内存分配失败,栈初始化失败!" << endl;exit(EXIT_FAILURE);}S.top = S.base; // 空栈:栈顶指针与栈底指针重合S.stacksize = MAXSIZE; // 初始容量S.increment = (incr > 0) ? incr : INCREMENT; // 确保扩容增量为正数
}
算法逻辑:
- 为栈分配初始内存(大小
MAXSIZE),base指向内存首地址; - 空栈时
top与base指向同一位置,stacksize记录初始容量,increment设置扩容步长; - 处理内存分配失败的异常(直接退出程序,避免后续错误)。时间复杂度:O (1)(仅内存分配和指针赋值)。
2. 判断栈空(StackEmpty)
bool StackEmpty(SqStack S) {return (S.base == S.top); // 栈顶与栈底重合 → 空栈
}
算法逻辑:栈的本质是 “top指针移动”:空栈时top未移动,与base指向同一位置,直接通过指针比较判断。时间复杂度:O(1)。
3. 判断栈满(StackFull)
bool StackFull(SqStack S) {return (S.top - S.base == S.stacksize); // 元素数量等于最大容量 → 栈满
}
算法逻辑:top - base计算当前元素数量(因top指向栈顶元素下一个位置,差值即元素个数),若等于stacksize则栈满。时间复杂度:O(1)。
4. 求栈长度(StackLength)
int StackLength(SqStack S) {return (S.top - S.base); // 指针差值即元素个数
}
算法逻辑:利用指针算术:top与base均指向同类型数组元素,差值即为两指针间的元素数量(栈中有效元素个数)。时间复杂度:O(1)。
5. 清空栈(ClearStack)
void ClearStack(SqStack &S) {if (S.base) { // 栈已初始化(base非空)S.top = S.base; // 重置栈顶指针至栈底 → 逻辑清空(不释放内存)}
}
算法逻辑:“清空” 是逻辑操作,无需删除元素或释放内存,只需将top指针重置为base,后续入栈会覆盖原有元素。时间复杂度:O(1)。
6. 销毁栈(DestroyStack)
void DestroyStack(SqStack &S) {if (S.base) { // 栈已初始化delete[] S.base; // 释放动态分配的数组内存S.base = S.top = nullptr; // 指针置空,避免野指针S.stacksize = 0; // 容量清零S.increment = 0; // 扩容增量清零}
}
算法逻辑:“销毁” 是物理操作,释放base指向的动态内存(彻底删除所有元素),并将所有指针和属性重置,避免内存泄漏。时间复杂度:O (1)(内存释放操作视为常数时间)。
7. 入栈(Push)
bool Push(SqStack &S, SElemType e) {// 栈满时尝试扩容,若扩容失败则入栈失败if (StackFull(S) && !ExpandStack(S)) {cerr << "栈已满且扩容失败,无法入栈!" << endl;return false;}*S.top++ = e; // 先将元素e存入top指向的位置,再将top指针后移一位return true;
}
算法逻辑:
- 检查栈是否已满:若满则调用
ExpandStack扩容,扩容失败则返回false; - 入栈操作:将元素
e存入top当前指向的位置,然后top指针后移(指向新的栈顶空位)。核心细节:*S.top++ = e等价于*S.top = e; S.top++;,符合栈顶指针 “先存后移” 的规则。时间复杂度:O (1)(无扩容时);O (n)(扩容时,需复制原数组元素,n 为当前栈容量)。
8. 出栈(Pop)
bool Pop(SqStack &S, SElemType &e) {if (StackEmpty(S)) { // 空栈无法出栈cerr << "栈为空,无法出栈!" << endl;return false;}e = *--S.top; // 先将top指针前移一位,再取出该位置的元素return true;
}
算法逻辑:
- 检查栈是否为空:空栈则返回
false; - 出栈操作:
top指针先前移一位(指向栈顶元素),再将该元素的值通过引用e返回。核心细节:e = *--S.top等价于S.top--; e = *S.top;,符合栈顶指针 “先移后取” 的规则。时间复杂度:O(1)。
9. 获取栈顶元素(GetTop)
bool GetTop(SqStack S, SElemType &e) {if (StackEmpty(S)) { // 空栈无栈顶元素cerr << "栈为空,无栈顶元素!" << endl;return false;}e = *(S.top - 1); // 栈顶元素在top指针的前一个位置return true;
}
算法逻辑:栈顶元素位于top指针的前一个位置(因top指向栈顶元素的下一个空位),直接通过S.top - 1访问,不移动top指针(与出栈的区别)。时间复杂度:O(1)。
三、扩展操作算法
1. 栈扩容(ExpandStack)
bool ExpandStack(SqStack &S) {// 分配新内存:原容量 + 扩容增量SElemType *newBase = new SElemType[S.stacksize + S.increment];if (!newBase) { // 内存分配失败cerr << "内存分配失败,栈扩容失败!" << endl;return false;}// 复制原栈元素到新内存(字节数 = 原容量 * 元素大小)memcpy(newBase, S.base, S.stacksize * sizeof(SElemType));delete[] S.base; // 释放原内存// 更新指针和容量:top指针位置 = 新基地址 + 原元素个数(top - base)S.top = newBase + (S.top - S.base);S.base = newBase; // 新基地址S.stacksize += S.increment; // 容量增加cout << "栈已扩容,新容量:" << S.stacksize << endl;return true;
}
算法逻辑:当栈满时,通过 “重新分配更大内存→复制原元素→释放旧内存→更新指针” 实现动态扩容:
- 分配大小为
stacksize + increment的新内存; - 用
memcpy复制原数组所有元素到新内存(保证数据不丢失); - 释放原内存,避免泄漏;
- 更新
base为新内存地址,top为新地址 + 原元素个数(保持栈顶位置不变),stacksize增加。时间复杂度:O (n)(n 为当前栈容量,因需复制所有元素)。空间复杂度:O (n + increment)(新内存大小)。
2. 栈遍历(TraverseStack)
void TraverseStack(SqStack S, void (*visit)(SElemType)) {if (StackEmpty(S)) {cout << "栈为空,无元素可遍历!" << endl;return;}SElemType *p = S.base; // 从栈底开始遍历cout << "栈元素(从栈底到栈顶):";while (p < S.top) { // 遍历至栈顶(top前一个位置)visit(*p++); // 调用回调函数处理元素(如打印),指针后移cout << " ";}cout << endl;
}// 回调函数:打印元素
void PrintElem(SElemType e) {cout << e;
}
算法逻辑:从栈底(base)到栈顶(top前一个位置)依次访问元素,通过回调函数visit处理元素(此处为打印):
- 遍历顺序:栈底→栈顶(与栈的 “后进先出” 特性无关,仅为完整访问所有元素);
- 灵活性:通过不同的
visit函数可实现多种遍历操作(如求和、查找等)。时间复杂度:O (n)(n 为栈长度,需访问每个元素)。
3. 栈复制(CopyStack)
bool CopyStack(SqStack S, SqStack &T) {DestroyStack(T); // 先销毁T的原有数据,避免内存泄漏// 为T分配与S相同的容量和扩容增量T.increment = S.increment;T.stacksize = S.stacksize;T.base = new SElemType[T.stacksize];if (!T.base) { // 内存分配失败cerr << "内存分配失败,栈复制失败!" << endl;return false;}// 复制元素:T的元素个数 = S的元素个数(top - base)T.top = T.base + (S.top - S.base);memcpy(T.base, S.base, (S.top - S.base) * sizeof(SElemType));return true;
}
算法逻辑:将栈S的所有元素和属性复制到栈T,保证T与S完全一致:
- 先销毁
T原有数据(避免内存泄漏); - 为
T分配与S相同的容量和扩容增量; - 复制
S的元素到T(通过memcpy),并设置T.top使元素个数与S相同。时间复杂度:O (n)(n 为S的长度,需复制所有元素)。
4. 栈比较(CompareStack)
bool CompareStack(SqStack S, SqStack T) {if (StackLength(S) != StackLength(T)) { // 长度不同则直接不等return false;}// 逐个比较元素(从栈底到栈顶)SElemType *p = S.base, *q = T.base;while (p < S.top && q < T.top) {if (*p++ != *q++) { // 有一个元素不同则不等return false;}}return true; // 长度相同且所有元素相同
}
算法逻辑:判断两个栈是否 “完全相等”(元素序列和长度均相同):
- 先比较长度:长度不同则直接返回
false; - 再逐个比较元素(从栈底到栈顶):若所有元素对应相等则返回
true,否则false。时间复杂度:O (n)(n 为栈长度,最坏情况需比较所有元素)。
四、典型应用:进制转换(Conversion)
void Conversion(int num, int base) {if (base < 2 || base > 16) { // 校验进制合法性(2-16进制)cerr << "进制必须在2-16之间!" << endl;return;}SqStack stack;InitStack(stack);int n = num;char digits[] = "0123456789ABCDEF"; // 16进制字符映射表// 特殊处理:0的转换if (n == 0) {Push(stack, 0);} else {bool isNegative = false;if (n < 0) { // 处理负数(先转为正数,最后加负号)isNegative = true;n = -n;}// 核心:除基取余法,余数入栈(后出栈即得转换结果)while (n > 0) {Push(stack, n % base); // 余数入栈n = n / base; // 商继续计算}if (isNegative) { // 负数标记cout << "-";}}// 出栈并打印结果(栈中余数的逆序即转换结果)cout << num << " 转换为 " << base << " 进制是:";SElemType e;while (Pop(stack, e)) {cout << digits[e]; // 用映射表输出字符(如10→A)}cout << endl;DestroyStack(stack); // 销毁临时栈
}
算法逻辑:利用栈的 “后进先出” 特性实现十进制到base进制(2-16)的转换,核心是 “除基取余法”:
- 原理:十进制数
num除以base,余数为base进制的低位,商继续除以base,直到商为 0;最后将余数逆序排列即得结果(栈恰好可实现 “逆序”)。 - 步骤:
- 处理特殊情况:
num=0直接入栈 0; - 处理负数:先转为正数,转换后加负号;
- 除基取余:
n = num,循环计算n % base(余数入栈)和n = n / base(商); - 出栈输出:栈中余数的出栈顺序即为转换结果的正确顺序(因先入栈的余数是低位,后出栈)。
- 处理特殊情况:
- 字符映射:用
digits数组将 10-15 映射为 'A'-'F'(支持 16 进制)。
时间复杂度:O (logₖn)(n 为十进制数大小,k 为目标进制,循环次数为 n 除以 k 的次数)。
五、顺序栈的基本操作的代码完整实现
(一)C++代码
#include <iostream>
#include <cstring>
#include <windows.h> // 引入Windows系统头文件
using namespace std;#define MAXSIZE 100 // 初始栈容量
#define INCREMENT 10 // 栈扩容增量// 栈元素类型定义(可根据需要修改为其他类型)
typedef int SElemType;// 顺序栈结构定义
typedef struct {SElemType *base; // 栈底指针SElemType *top; // 栈顶指针(指向栈顶元素的下一个位置)int stacksize; // 当前栈的最大容量int increment; // 扩容增量(可动态调整)
} SqStack;// 函数声明
void InitStack(SqStack &S, int incr = INCREMENT); // 初始化栈(可指定扩容增量)
bool StackEmpty(SqStack S); // 判断栈是否为空
bool StackFull(SqStack S); // 判断栈是否已满
int StackLength(SqStack S); // 获取栈长度
void ClearStack(SqStack &S); // 清空栈
void DestroyStack(SqStack &S); // 销毁栈
bool Push(SqStack &S, SElemType e); // 入栈(支持自动扩容)
bool Pop(SqStack &S, SElemType &e); // 出栈(通过引用返回元素)
bool GetTop(SqStack S, SElemType &e); // 获取栈顶元素(通过引用返回)
void TraverseStack(SqStack S, void (*visit)(SElemType)); // 遍历栈元素
bool ExpandStack(SqStack &S); // 栈扩容
bool CopyStack(SqStack S, SqStack &T); // 复制栈(S复制到T)
bool CompareStack(SqStack S, SqStack T); // 比较两个栈是否相等
void Conversion(int num, int base); // 应用:进制转换(利用栈)
void PrintElem(SElemType e); // 声明PrintElem函数,用于遍历// 测试函数
int main() {SetConsoleOutputCP(CP_UTF8); // 强制控制台使用UTF-8解析输出SqStack S, T;SElemType e;// 初始化栈InitStack(S, 20); // 自定义扩容增量为20cout << "初始化栈S完成,初始容量:" << S.stacksize << endl;// 测试入栈cout << "\n=== 入栈测试 ===" << endl;for (int i = 1; i <= 150; i++) { // 超过初始容量,测试扩容if (Push(S, i)) {if (i % 30 == 0) { // 每30个元素打印一次状态cout << "已入栈" << i << "个元素,当前栈长度:" << StackLength(S) << endl;}}}// 测试遍历cout << "\n=== 遍历测试 ===" << endl;TraverseStack(S, PrintElem);// 测试栈顶元素cout << "\n=== 栈顶元素测试 ===" << endl;if (GetTop(S, e)) {cout << "当前栈顶元素:" << e << endl;}// 测试出栈cout << "\n=== 出栈测试 ===" << endl;for (int i = 0; i < 5; i++) {if (Pop(S, e)) {cout << "出栈元素:" << e << ",剩余栈长度:" << StackLength(S) << endl;}}// 测试复制栈cout << "\n=== 复制栈测试 ===" << endl;if (CopyStack(S, T)) {cout << "栈S复制到栈T成功!" << endl;cout << "栈T的元素:";TraverseStack(T, PrintElem);}// 测试比较栈cout << "\n=== 比较栈测试 ===" << endl;cout << "栈S和栈T是否相等:" << (CompareStack(S, T) ? "是" : "否") << endl;Push(T, 999); // 修改栈Tcout << "栈T添加元素999后,是否相等:" << (CompareStack(S, T) ? "是" : "否") << endl;// 测试清空栈cout << "\n=== 清空栈测试 ===" << endl;ClearStack(S);cout << "清空栈S后,栈是否为空:" << (StackEmpty(S) ? "是" : "否") << endl;// 测试进制转换应用cout << "\n=== 进制转换测试 ===" << endl;Conversion(123, 2); // 十进制123转二进制Conversion(255, 16); // 十进制255转十六进制Conversion(-100, 8); // 十进制-100转八进制Conversion(0, 10); // 十进制0转十进制// 销毁栈DestroyStack(S);DestroyStack(T);cout << "\n所有栈已销毁,程序结束!" << endl;return 0;
}// 初始化栈
void InitStack(SqStack &S, int incr) {S.base = new SElemType[MAXSIZE];if (!S.base) {cerr << "内存分配失败,栈初始化失败!" << endl;exit(EXIT_FAILURE);}S.top = S.base;S.stacksize = MAXSIZE;S.increment = (incr > 0) ? incr : INCREMENT; // 确保扩容增量为正数
}// 判断栈是否为空
bool StackEmpty(SqStack S) {return (S.base == S.top);
}// 判断栈是否已满
bool StackFull(SqStack S) {return (S.top - S.base == S.stacksize);
}// 获取栈长度
int StackLength(SqStack S) {return (S.top - S.base);
}// 清空栈
void ClearStack(SqStack &S) {if (S.base) {S.top = S.base; // 仅需重置栈顶指针}
}// 销毁栈
void DestroyStack(SqStack &S) {if (S.base) {delete[] S.base; // 释放堆内存S.base = S.top = nullptr; // 避免野指针S.stacksize = 0;S.increment = 0;}
}// 栈扩容
bool ExpandStack(SqStack &S) {SElemType *newBase = new SElemType[S.stacksize + S.increment];if (!newBase) {cerr << "内存分配失败,栈扩容失败!" << endl;return false;}// 复制原有元素memcpy(newBase, S.base, S.stacksize * sizeof(SElemType));// 释放旧内存delete[] S.base;// 更新栈指针和容量S.top = newBase + (S.top - S.base);S.base = newBase;S.stacksize += S.increment;cout << "栈已扩容,新容量:" << S.stacksize << endl;return true;
}// 入栈(支持自动扩容)
bool Push(SqStack &S, SElemType e) {// 栈满时尝试扩容if (StackFull(S) && !ExpandStack(S)) {cerr << "栈已满且扩容失败,无法入栈!" << endl;return false;}*S.top++ = e; // 先赋值后移动栈顶指针return true;
}// 出栈(通过引用返回元素)
bool Pop(SqStack &S, SElemType &e) {if (StackEmpty(S)) {cerr << "栈为空,无法出栈!" << endl;return false;}e = *--S.top; // 先移动栈顶指针后取值return true;
}// 获取栈顶元素(通过引用返回)
bool GetTop(SqStack S, SElemType &e) {if (StackEmpty(S)) {cerr << "栈为空,无栈顶元素!" << endl;return false;}e = *(S.top - 1); // 栈顶指针前一个位置是栈顶元素return true;
}// 遍历栈元素(从栈底到栈顶)
void TraverseStack(SqStack S, void (*visit)(SElemType)) {if (StackEmpty(S)) {cout << "栈为空,无元素可遍历!" << endl;return;}SElemType *p = S.base;cout << "栈元素(从栈底到栈顶):";while (p < S.top) {visit(*p++);cout << " ";}cout << endl;
}// 显示元素的函数(用于遍历)
void PrintElem(SElemType e) {cout << e;
}// 复制栈(将栈S复制到栈T)
bool CopyStack(SqStack S, SqStack &T) {// 先销毁T的原有数据DestroyStack(T);// 初始化T,容量与S相同T.increment = S.increment;T.stacksize = S.stacksize;T.base = new SElemType[T.stacksize];if (!T.base) {cerr << "内存分配失败,栈复制失败!" << endl;return false;}// 复制元素T.top = T.base + (S.top - S.base);memcpy(T.base, S.base, (S.top - S.base) * sizeof(SElemType));return true;
}// 比较两个栈是否相等(元素序列和长度均相同)
bool CompareStack(SqStack S, SqStack T) {// 长度不同则直接不等if (StackLength(S) != StackLength(T)) {return false;}// 逐个比较元素SElemType *p = S.base, *q = T.base;while (p < S.top && q < T.top) {if (*p++ != *q++) {return false;}}return true;
}// 应用:利用栈实现进制转换(十进制转base进制,base在2-16之间)
void Conversion(int num, int base) {if (base < 2 || base > 16) {cerr << "进制必须在2-16之间!" << endl;return;}SqStack stack;InitStack(stack);int n = num;char digits[] = "0123456789ABCDEF"; // 16进制以下的数字字符// 特殊情况:0的转换if (n == 0) {Push(stack, 0);} else {// 处理负数bool isNegative = false;if (n < 0) {isNegative = true;n = -n;}// 取余入栈while (n > 0) {Push(stack, n % base);n = n / base;}// 负数标记if (isNegative) {cout << "-";}}// 出栈并打印结果cout << num << " 转换为 " << base << " 进制是:";SElemType e;while (Pop(stack, e)) {cout << digits[e];}cout << endl;DestroyStack(stack);
}
(二)Python代码
class SqStack:def __init__(self, increment=10):"""初始化栈"""self.MAXSIZE = 100 # 初始栈容量self.base = [0] * self.MAXSIZE # 栈底(用列表模拟动态数组)self.top = 0 # 栈顶指针(指向栈顶元素的下一个位置,初始为0)self.stacksize = self.MAXSIZE # 当前栈的最大容量self.increment = increment if increment > 0 else 10 # 扩容增量def is_empty(self):"""判断栈是否为空"""return self.top == 0def is_full(self):"""判断栈是否已满"""return self.top == self.stacksizedef length(self):"""获取栈长度"""return self.topdef clear(self):"""清空栈"""self.top = 0 # 仅重置栈顶指针def destroy(self):"""销毁栈"""self.base = []self.top = 0self.stacksize = 0self.increment = 0def expand(self):"""栈扩容"""try:# 创建新的更大容量的列表new_base = [0] * (self.stacksize + self.increment)# 复制原有元素for i in range(self.stacksize):new_base[i] = self.base[i]# 更新栈属性self.base = new_baseself.stacksize += self.incrementprint(f"栈已扩容,新容量:{self.stacksize}")return Trueexcept MemoryError:print("内存分配失败,栈扩容失败!")return Falsedef push(self, e):"""入栈(支持自动扩容)"""# 栈满时尝试扩容if self.is_full() and not self.expand():print("栈已满且扩容失败,无法入栈!")return Falseself.base[self.top] = eself.top += 1return Truedef pop(self):"""出栈(返回元素和操作结果)"""if self.is_empty():print("栈为空,无法出栈!")return None, Falseself.top -= 1return self.base[self.top], Truedef get_top(self):"""获取栈顶元素"""if self.is_empty():print("栈为空,无栈顶元素!")return None, Falsereturn self.base[self.top - 1], Truedef traverse(self, visit_func):"""遍历栈元素(从栈底到栈顶)"""if self.is_empty():print("栈为空,无元素可遍历!")returnprint("栈元素(从栈底到栈顶):", end="")for i in range(self.top):visit_func(self.base[i])print(" ", end="")print()def print_elem(e):"""用于遍历的打印函数"""print(e, end="")def copy_stack(s):"""复制栈(s复制到新栈)"""t = SqStack(s.increment)# 销毁原有数据(在Python中只需重置即可)t.base = [0] * s.stacksizet.stacksize = s.stacksizet.top = s.top# 复制元素for i in range(s.top):t.base[i] = s.base[i]return tdef compare_stack(s, t):"""比较两个栈是否相等"""if s.length() != t.length():return Falsefor i in range(s.top):if s.base[i] != t.base[i]:return Falsereturn Truedef conversion(num, base):"""应用:利用栈实现进制转换(十进制转base进制,base在2-16之间)"""if base < 2 or base > 16:print("进制必须在2-16之间!")returnstack = SqStack()n = numdigits = "0123456789ABCDEF" # 16进制以下的数字字符# 特殊情况:0的转换if n == 0:stack.push(0)else:# 处理负数is_negative = Falseif n < 0:is_negative = Truen = -n# 取余入栈while n > 0:stack.push(n % base)n = n // base# 负数标记if is_negative:print("-", end="")# 出栈并打印结果print(f"{num} 转换为 {base} 进制是:", end="")while not stack.is_empty():elem, _ = stack.pop()print(digits[elem], end="")print()# 测试函数
def main():# 初始化栈s = SqStack(20) # 自定义扩容增量为20print(f"初始化栈S完成,初始容量:{s.stacksize}")# 测试入栈print("\n=== 入栈测试 ===")for i in range(1, 151): # 超过初始容量,测试扩容if s.push(i):if i % 30 == 0: # 每30个元素打印一次状态print(f"已入栈{i}个元素,当前栈长度:{s.length()}")# 测试遍历print("\n=== 遍历测试 ===")s.traverse(print_elem)# 测试栈顶元素print("\n=== 栈顶元素测试 ===")top_elem, success = s.get_top()if success:print(f"当前栈顶元素:{top_elem}")# 测试出栈print("\n=== 出栈测试 ===")for _ in range(5):elem, success = s.pop()if success:print(f"出栈元素:{elem},剩余栈长度:{s.length()}")# 测试复制栈print("\n=== 复制栈测试 ===")t = copy_stack(s)print("栈S复制到栈T成功!")print("栈T的元素:", end="")t.traverse(print_elem)# 测试比较栈print("\n=== 比较栈测试 ===")print(f"栈S和栈T是否相等:{'是' if compare_stack(s, t) else '否'}")t.push(999) # 修改栈Tprint(f"栈T添加元素999后,是否相等:{'是' if compare_stack(s, t) else '否'}")# 测试清空栈print("\n=== 清空栈测试 ===")s.clear()print(f"清空栈S后,栈是否为空:{'是' if s.is_empty() else '否'}")# 测试进制转换应用print("\n=== 进制转换测试 ===")conversion(123, 2) # 十进制123转二进制conversion(255, 16) # 十进制255转十六进制conversion(-100, 8) # 十进制-100转八进制conversion(0, 10) # 十进制0转十进制# 销毁栈s.destroy()t.destroy()print("\n所有栈已销毁,程序结束!")if __name__ == "__main__":main()(三)Java代码
import java.util.Arrays;// 顺序栈类实现
public class SqStack {private int[] base; // 栈底(用数组模拟)private int top; // 栈顶指针(指向栈顶元素的下一个位置)private int stacksize; // 当前栈的最大容量private int increment; // 扩容增量private static final int MAXSIZE = 100; // 初始栈容量private static final int DEFAULT_INCREMENT = 10; // 默认扩容增量// 构造函数(可指定扩容增量)public SqStack(int incr) {this.increment = incr > 0 ? incr : DEFAULT_INCREMENT;this.base = new int[MAXSIZE];this.top = 0;this.stacksize = MAXSIZE;}// 默认构造函数public SqStack() {this(DEFAULT_INCREMENT);}// 判断栈是否为空public boolean isEmpty() {return top == 0;}// 判断栈是否已满public boolean isFull() {return top == stacksize;}// 获取栈长度public int length() {return top;}// 清空栈public void clear() {top = 0; // 仅重置栈顶指针}// 销毁栈(Java中由垃圾回收机制处理,这里仅做重置)public void destroy() {base = null;top = 0;stacksize = 0;increment = 0;}// 栈扩容private boolean expand() {try {// 创建新的更大容量的数组int newSize = stacksize + increment;int[] newBase = new int[newSize];// 复制原有元素System.arraycopy(base, 0, newBase, 0, stacksize);// 更新栈属性base = newBase;stacksize = newSize;System.out.println("栈已扩容,新容量:" + stacksize);return true;} catch (OutOfMemoryError e) {System.err.println("内存分配失败,栈扩容失败!");return false;}}// 入栈(支持自动扩容)public boolean push(int e) {// 栈满时尝试扩容if (isFull() && !expand()) {System.err.println("栈已满且扩容失败,无法入栈!");return false;}base[top++] = e;return true;}// 出栈(返回元素,通过返回值null表示失败)public Integer pop() {if (isEmpty()) {System.err.println("栈为空,无法出栈!");return null;}return base[--top];}// 获取栈顶元素(返回元素,通过返回值null表示失败)public Integer getTop() {if (isEmpty()) {System.err.println("栈为空,无栈顶元素!");return null;}return base[top - 1];}// 遍历栈元素(从栈底到栈顶)public void traverse(VisitFunction visitor) {if (isEmpty()) {System.out.println("栈为空,无元素可遍历!");return;}System.out.print("栈元素(从栈底到栈顶):");for (int i = 0; i < top; i++) {visitor.visit(base[i]);System.out.print(" ");}System.out.println();}// 函数式接口:用于遍历操作@FunctionalInterfacepublic interface VisitFunction {void visit(int e);}// 复制栈(复制当前栈到新栈)public static SqStack copyStack(SqStack s) {SqStack t = new SqStack(s.increment);// 销毁原有数据并重新初始化t.stacksize = s.stacksize;t.base = new int[t.stacksize];t.top = s.top;// 复制元素System.arraycopy(s.base, 0, t.base, 0, s.top);return t;}// 比较两个栈是否相等public static boolean compareStack(SqStack s, SqStack t) {if (s.length() != t.length()) {return false;}for (int i = 0; i < s.top; i++) {if (s.base[i] != t.base[i]) {return false;}}return true;}// 应用:利用栈实现进制转换(十进制转base进制,base在2-16之间)public static void conversion(int num, int base) {if (base < 2 || base > 16) {System.err.println("进制必须在2-16之间!");return;}SqStack stack = new SqStack();int n = num;char[] digits = "0123456789ABCDEF".toCharArray(); // 16进制以下的数字字符// 特殊情况:0的转换if (n == 0) {stack.push(0);} else {// 处理负数boolean isNegative = false;if (n < 0) {isNegative = true;n = -n;}// 取余入栈while (n > 0) {stack.push(n % base);n = n / base;}// 负数标记if (isNegative) {System.out.print("-");}}// 出栈并打印结果System.out.print(num + " 转换为 " + base + " 进制是:");while (!stack.isEmpty()) {int elem = stack.pop();System.out.print(digits[elem]);}System.out.println();stack.destroy();}// 测试函数public static void main(String[] args) {// 初始化栈SqStack s = new SqStack(20); // 自定义扩容增量为20System.out.println("初始化栈S完成,初始容量:" + s.stacksize);// 测试入栈System.out.println("\n=== 入栈测试 ===");for (int i = 1; i <= 150; i++) { // 超过初始容量,测试扩容if (s.push(i)) {if (i % 30 == 0) { // 每30个元素打印一次状态System.out.println("已入栈" + i + "个元素,当前栈长度:" + s.length());}}}// 测试遍历System.out.println("\n=== 遍历测试 ===");s.traverse(e -> System.out.print(e));// 测试栈顶元素System.out.println("\n\n=== 栈顶元素测试 ===");Integer topElem = s.getTop();if (topElem != null) {System.out.println("当前栈顶元素:" + topElem);}// 测试出栈System.out.println("\n=== 出栈测试 ===");for (int i = 0; i < 5; i++) {Integer elem = s.pop();if (elem != null) {System.out.println("出栈元素:" + elem + ",剩余栈长度:" + s.length());}}// 测试复制栈System.out.println("\n=== 复制栈测试 ===");SqStack t = copyStack(s);System.out.println("栈S复制到栈T成功!");System.out.print("栈T的元素:");t.traverse(e -> System.out.print(e));System.out.println();// 测试比较栈System.out.println("\n=== 比较栈测试 ===");System.out.println("栈S和栈T是否相等:" + (compareStack(s, t) ? "是" : "否"));t.push(999); // 修改栈TSystem.out.println("栈T添加元素999后,是否相等:" + (compareStack(s, t) ? "是" : "否"));// 测试清空栈System.out.println("\n=== 清空栈测试 ===");s.clear();System.out.println("清空栈S后,栈是否为空:" + (s.isEmpty() ? "是" : "否"));// 测试进制转换应用System.out.println("\n=== 进制转换测试 ===");conversion(123, 2); // 十进制123转二进制conversion(255, 16); // SqStack十进制255转十六进制conversion(-100, 8); // 十进制-100转八进制conversion(0, 10); // 十进制0转十进制// 销毁栈s.destroy();t.destroy();System.out.println("\n所有栈已销毁,程序结束!");}
}
六、程序运行结果展示
(一)C++程序运行截图
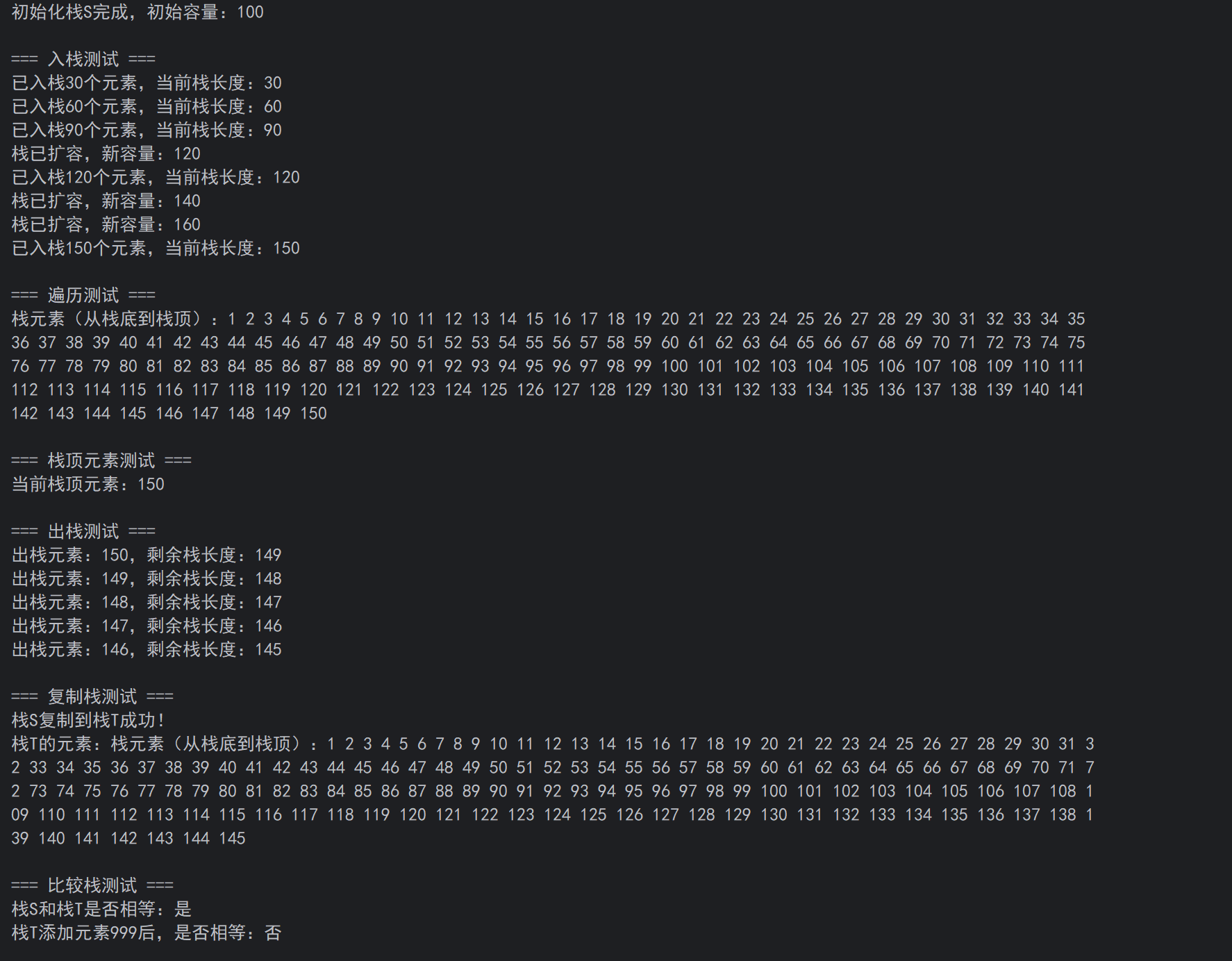
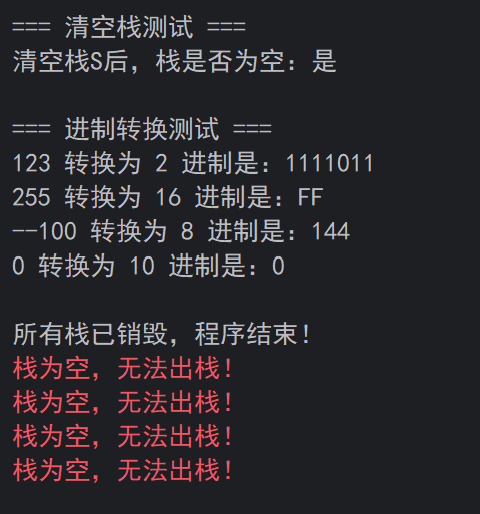
(二)Python程序运行截图
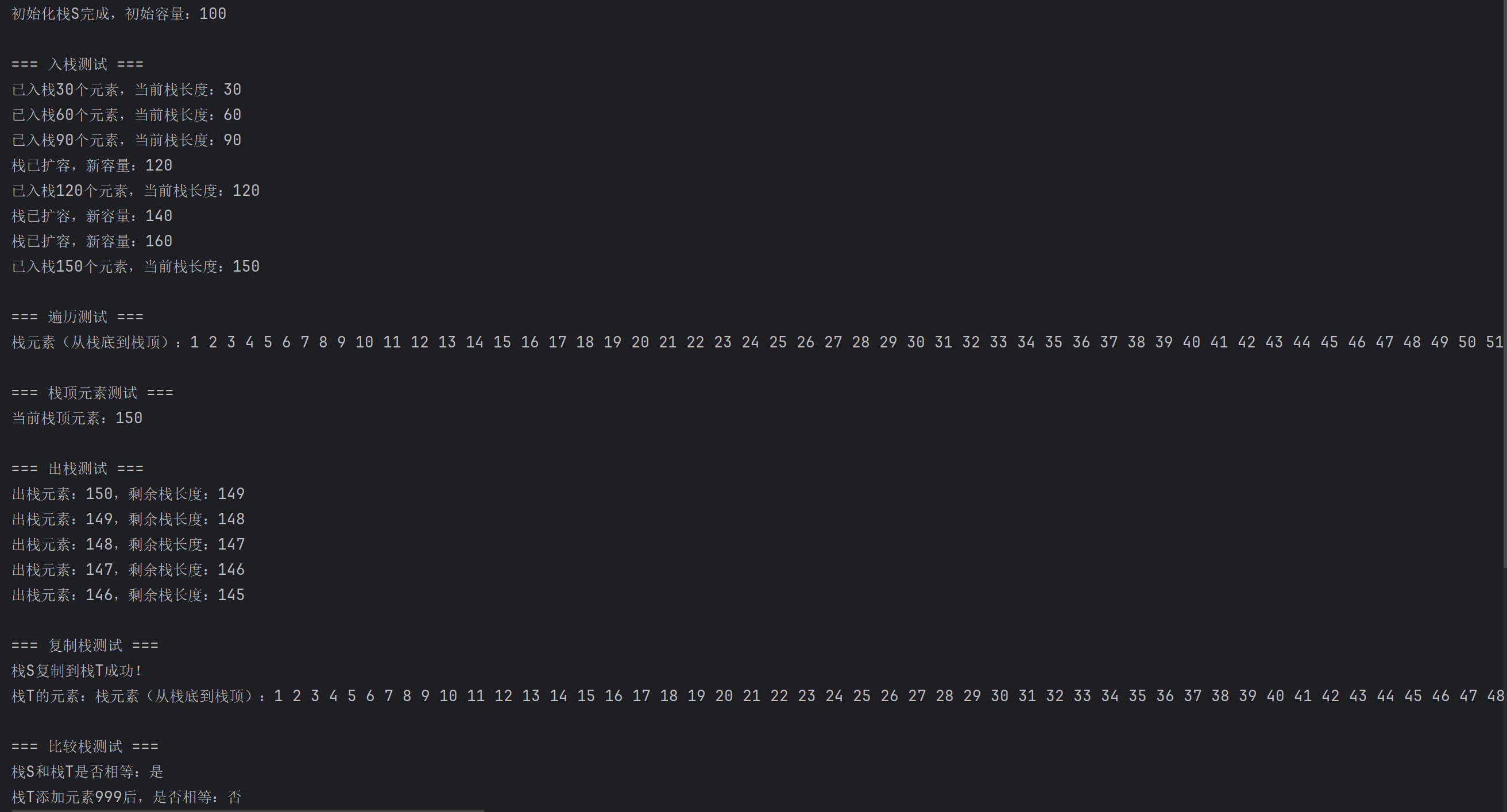

(三)Java程序运行截图
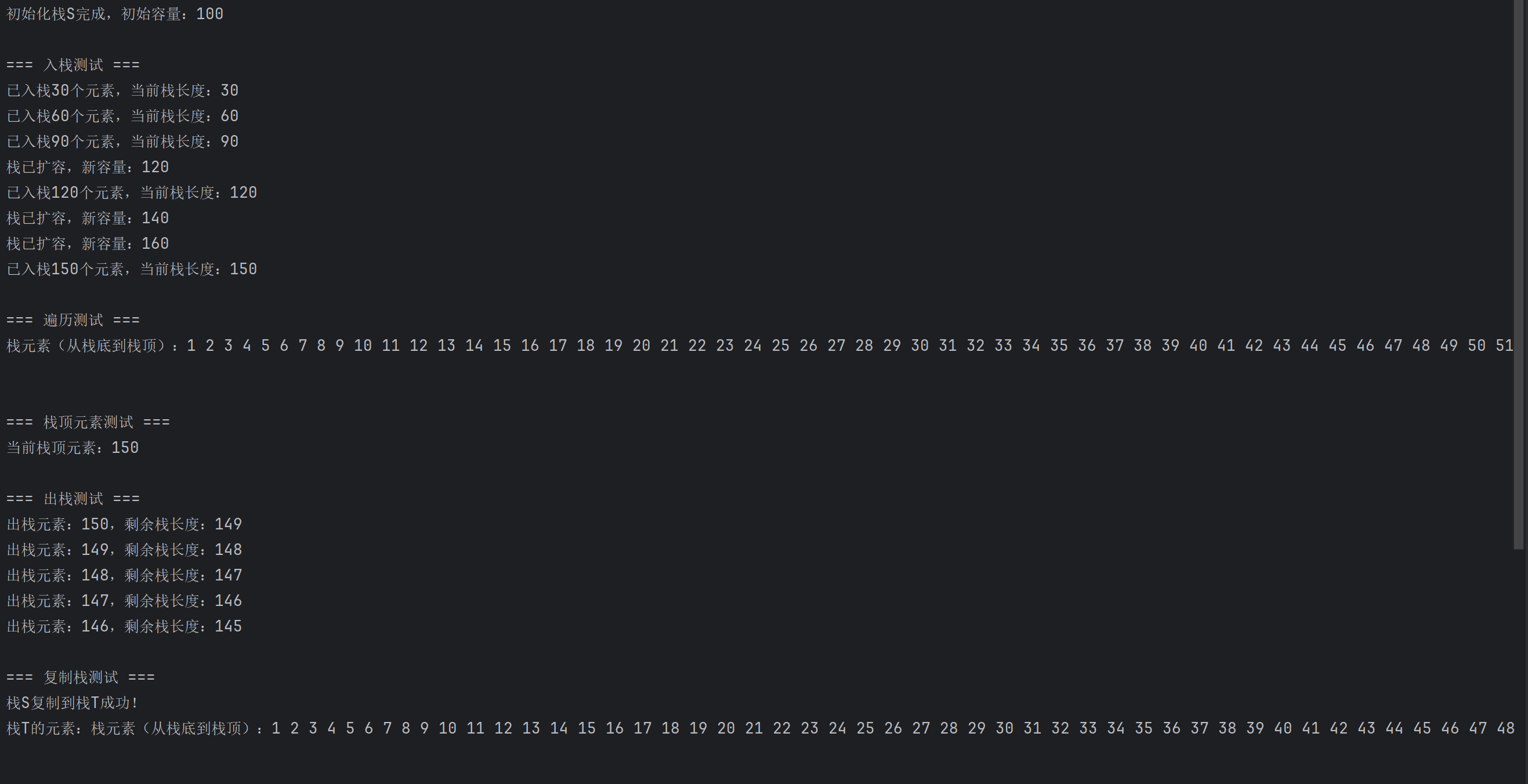

七、算法整体总结
该代码通过 “动态数组 + 指针” 实现了顺序栈的完整操作,核心算法围绕栈的 “后进先出” 特性展开:
- 基础操作:通过指针移动实现元素的入栈、出栈等,时间复杂度均为 O (1)(无扩容时);
- 扩展操作:扩容、复制等涉及元素复制,时间复杂度为 O (n),但保证了栈的灵活性;
- 典型应用:进制转换利用栈的逆序特性,高效实现数制转换,体现了栈在 “逆序处理” 场景中的优势。
整体设计兼顾了功能性(完整操作集)、健壮性(异常处理、内存管理)和扩展性(可修改元素类型、扩容增量),是顺序栈实现的经典案例。
