当前位置：首页 > news >正文

Numpy 手搓线性回归

news 2025/10/5 6:27:30

生成模拟数据

import numpy as np
import matplotlib.pyplot as plt
# 生成模拟数据
np.random.seed(42)
X = 2 * np.random.rand(200, 1) # 200 行、1 列的二维数组，就是200个x
Y = 4 + 3 * X + np.random.randn(200, 1)
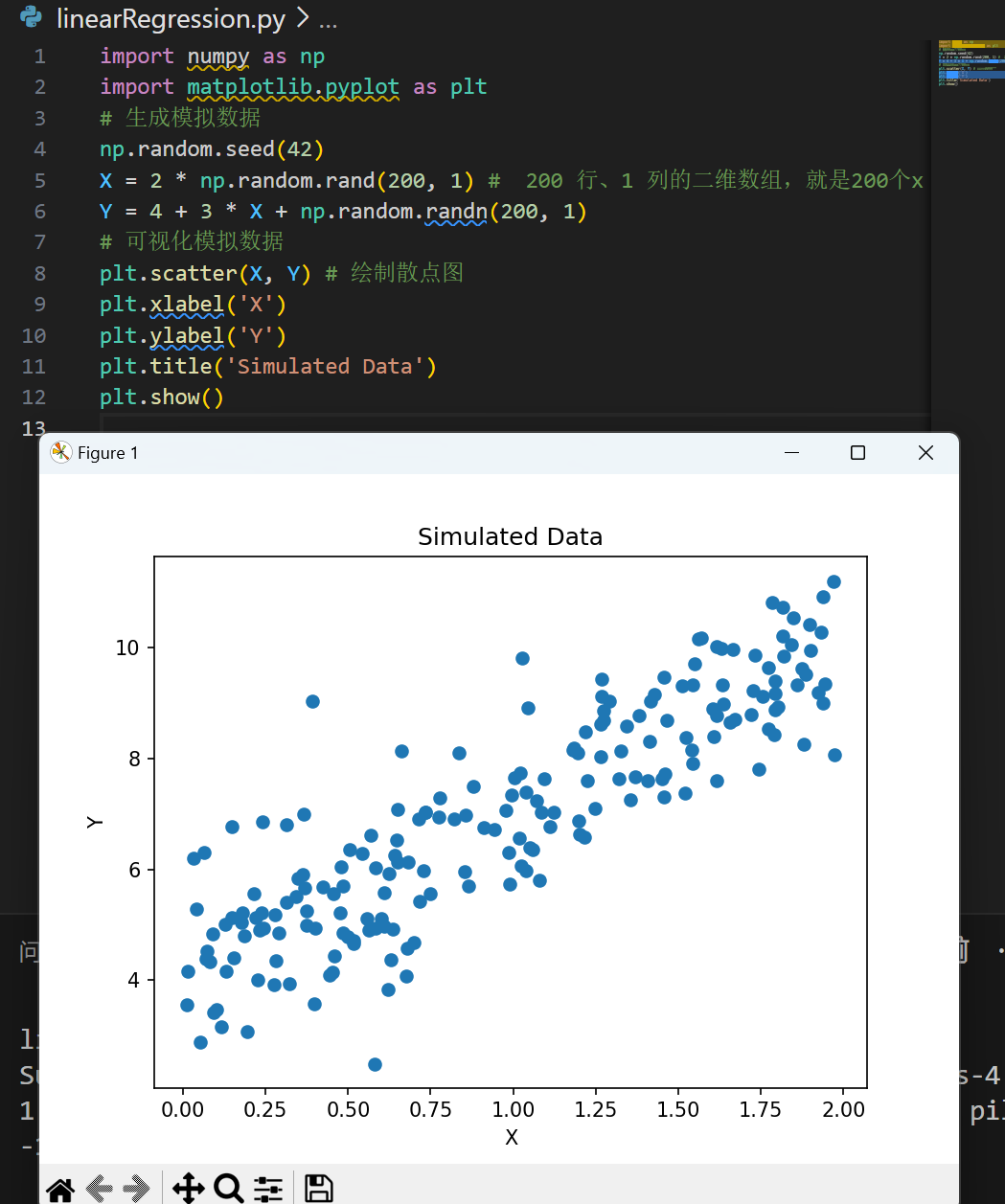
# 可视化模拟数据
plt.scatter(X, Y) # 绘制散点图
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Simulated Data')
plt.show()

以梯度下降完成线性回归

# 将偏执项b作为一个特征融入矩阵运算
b_X = np.c_[np.ones((200, 1)),X]
# 定义学习率，迭代次数和样本数量
rate = 0.01
iterations = 1000
m = 200
# 参数theta
theta = np.random.randn(2, 1)
# 损失函数的梯度下降
for _ in range(iterations):
temp = 1/m * b_X.T.dot( b_X.dot(theta) - Y)
theta = theta - rate * temp
X_new = np.array([[0], [2]]) # 覆盖原始X的取值范围（0到2）
X_new_b = np.c_[np.ones((2, 1)), X_new] # 同样添加偏置项列（全为1）
y_hat = X_new_b.dot(theta) # 计算预测值
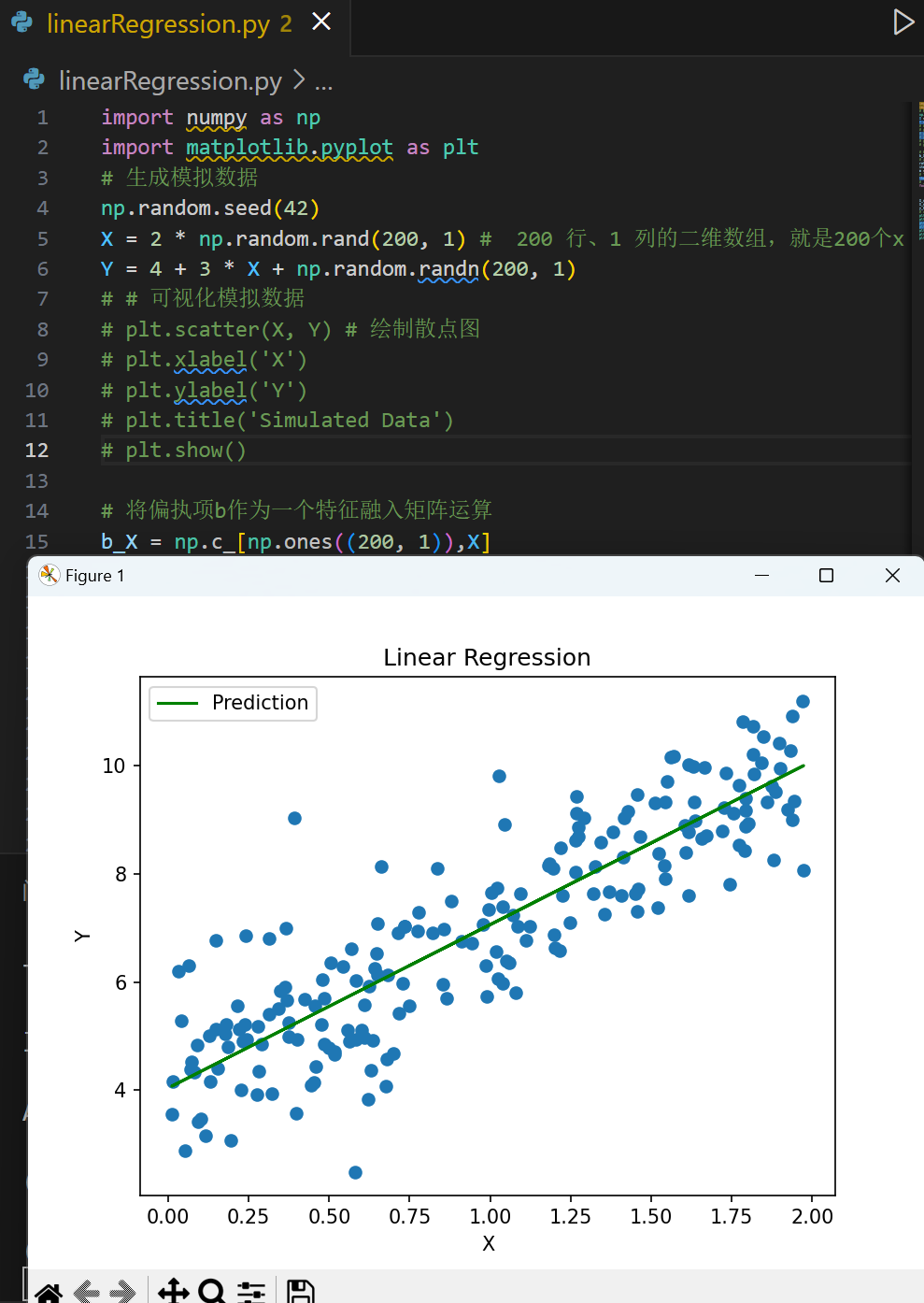
# 绘制图像
plt.plot(X, b_X.dot(theta), 'g-', label='Prediction')
plt.scatter(X, Y)
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.title('Linear Regression')
plt.show()

绘制结果

完整代码

import numpy as np
import matplotlib.pyplot as plt
# 生成模拟数据
np.random.seed(42)
X = 2 * np.random.rand(200, 1) # 200 行、1 列的二维数组，就是200个x
Y = 4 + 3 * X + np.random.randn(200, 1)
# # 可视化模拟数据
# plt.scatter(X, Y) # 绘制散点图
# plt.xlabel('X')
# plt.ylabel('Y')
# plt.title('Simulated Data')
# plt.show()
# 将偏执项b作为一个特征融入矩阵运算
b_X = np.c_[np.ones((200, 1)),X]
# 定义学习率，迭代次数和样本数量
rate = 0.01
iterations = 1000
m = 200
# 参数theta
theta = np.random.randn(2, 1)
# 损失函数的梯度下降
for _ in range(iterations):
temp = 1/m * b_X.T.dot( b_X.dot(theta) - Y)
theta = theta - rate * temp
X_new = np.array([[0], [2]]) # 覆盖原始X的取值范围（0到2）
X_new_b = np.c_[np.ones((2, 1)), X_new] # 同样添加偏置项列（全为1）
y_hat = X_new_b.dot(theta) # 计算预测值
# 绘制图像
plt.plot(X, b_X.dot(theta), 'g-', label='Prediction')
plt.scatter(X, Y)
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.title('Linear Regression')
plt.show()