Codeforces Round 1052 (Div. 2) C. Wrong Binary Searchong Binary Search

题目意思：

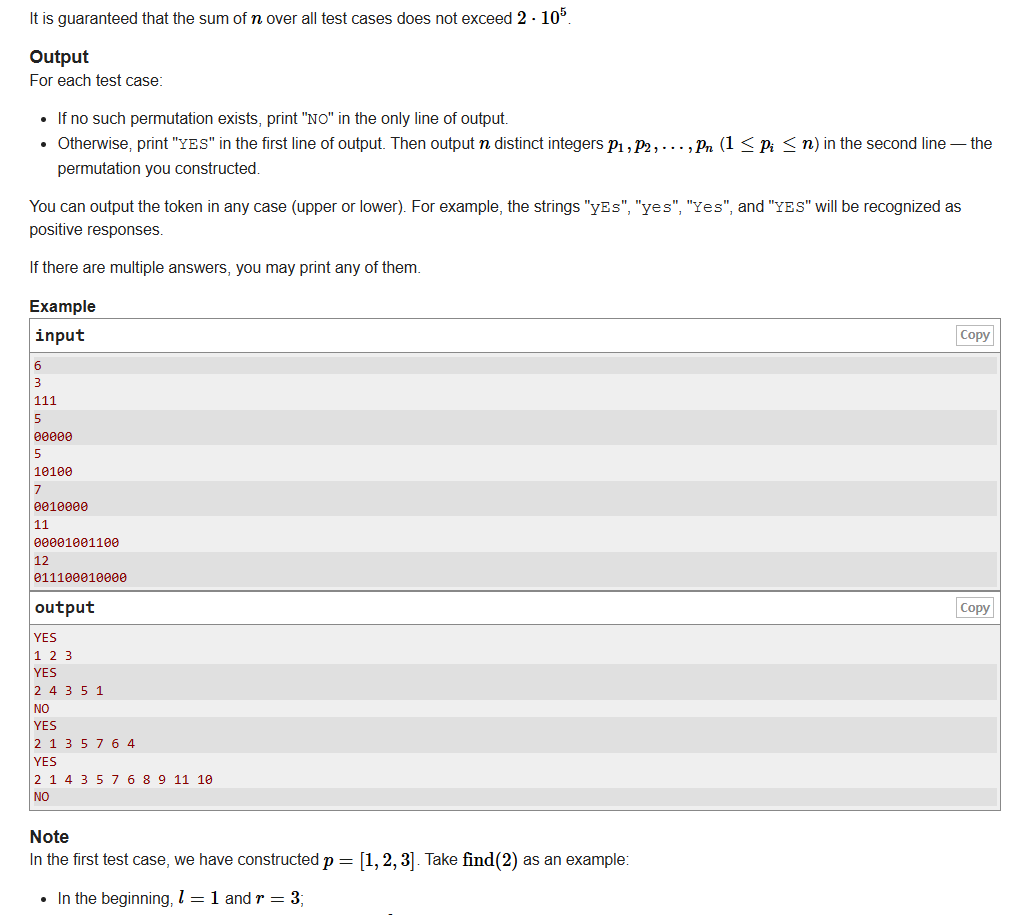
给一个二进制字符串，字符串下标从1开始，如果s[i]为1则i为稳定点，反正为不稳定点，需要我们依据伪代码构造一个长度为n的排序，使得排序中的每个数都满足对应s中的稳定点与不稳定点。

思路：

伪代码二分原理：
fun(x)
m为区间[l,r]上一个点
如果 p[m]==x，返回m
否则：
如果区间右端点的值大于p[m]，r=m-1
否则 l=m+1

简单地说：
伪代码只会判断p[m]是否大于x！！！
伪代码只会判断p[m]是否大于x！！！
伪代码只会判断p[m]是否大于x！！！
若大于x就缩短右边界
反正缩短做左边界

而对于稳定点：
当且仅当find(x)==x时，x才为稳定点，也就是p[x]=x
若find(x)!=x，或未定义，那么x都是不稳定点，也就是p[x]!=x
要使得i点为稳定点，首先必须保证p[i]=i;

之后就要让伪代码能搜到结点i
因为伪代码任取一点m,只会判断p[m]是否大于x，如果比i大就收缩右端点
如果比i小就收缩左端点
因此只要i在区间[l,r]上就必须保证[l,i-1]上的数都小于i，[i+1,r]上的数都大于i
这样就可以使得无论在区间上取到哪个数，无论怎么收缩，i都包含在收缩后的边界内，直至搜到i
然而在所有的稳定点必然是按照从小到大排列的基础上：

1.相邻稳定点之间：如果有非稳定点，则非稳定点个数一定>=2，即2相邻稳定点之间距离=2时无效
证：
如果非稳定点个数=1，举例：s=101的情况下，1为稳定点，2为不稳定点，3为稳定点
在p[1]=1,p[3]=3的基础上，p[2]只能为2
那么p=123，结点2就成了稳定点，与s=101不符

如果非稳定点个数>=2，如非稳定点个数=2，举例：s=1001,1为稳定点，2为不稳定点，3为不稳定点 4为稳定点
下标区间[2,3]只要做到比1大，比4小即可，那么 p=1324 同样可以保证 1,4稳定，2,3不稳定
因为伪代码任取一点m,只会判断p[m]是否大于x，
区间上除1之外的所有点都是比1大的，所以在搜索1时只会不断收缩右边界，直至搜到1
区间上除4之外的所有点都是比4大的，所以在搜索4时只会不断收缩左边界，直至搜到4
非稳定点个数>2时同理

2.最小稳定点之前：如果有非稳定点，则非稳定点个数一定>=2，即第一个稳定点为2时无效
如果非稳定点个数=1，举例：s=011的情况下，1为不稳定点，2为稳定点，3为稳定点
p[1]的位置只能是1，此时i就成了稳定点，与s不符

如果非稳定点个数>=2，如非稳定点个数=2，举例：s=0011,1为不稳定点，2为不稳定点，3为稳定点 4为稳定点
p可以为1234,也可以为2134；当p=2134时，因为所有数都比3，4小所以会不断收缩左边界
非稳定点个数>2时同理

3.最大稳定点之后：如果有非稳定点，则非稳定点个数一定>=2，即最后一个稳定点为n-1时无效
证明过程同2.

在上述推导过程中不难看出，在构造排序时，可以利用稳定点将整个排序拆分成若干子区间
在子区间上逆序构造排序即可

AC代码：

#include<iostream>
#include<vector>
using namespace std;
vector<int> a;//存储所有稳定点
vector<int> p;
void build(int l, int r) {//构造函数int len = r - l + 1;if (len % 2 == 0) {for (int i = r;i >= l;i--) {p.push_back(i);}}else {int k = (r + l) / 2;for (int i = r;i >= l;i--) {if (i != k) {p.push_back(i);}}p.push_back(k);}
}
int main() {int t;cin >> t;getchar();while (t--) {a.clear();p.clear();int n;cin >> n;getchar();string s;cin >> s;a.push_back(0);for (int i = 0;i < n;i++) {if (s[i] == '1') {a.push_back(i + 1);}}if (a.size() == 1) {//没有稳定点cout << "YES" << endl;for (int i = n;i >= 1;i--) {cout << i << " ";}cout << endl;}else if (a.size() == n + 1) {//所有点都是稳定点cout << "YES" << endl;for (int i = 1;i <= n;i++) {cout << i << " ";}cout << endl;}else {bool flag = 1;int ll = a[1];//第一个稳定点int rr = a.back();//最后一个稳定点if (ll == 2 || rr == n - 1) {cout << "NO" << endl;continue;}for (int i = 1;i < a.size();i++) {if (a[i] - a[i - 1] == 2) {//稳定点之间距离=2且不为0flag = 0;break;}}if (!flag) {cout << "NO" << endl;}else {	cout << "YES" << endl;//  构造排序for (int i = 1;i < a.size();i++) {int l = a[i - 1] + 1;int r = a[i] - 1;if (l < r) {build(l, r);}p.push_back(a[i]);}if (a.back() < n) {//处理末尾int l = a.back() + 1;int r = n;build(l, r);}for (int i : p) {cout << i << " ";}cout << endl;}}}return 0;
}