当前位置：首页 > news >正文

伽利略 | 近代科学的奠定 / 函数观念的演变

news 2025/9/29 6:10:25

注：本文为 “伽利略 | 近代科学奠定 / 函数观念演变” 相关合辑。
略作重排，如有内容异常，请看原文。

伽利略是如何奠定近代科学的？| 贤说八道

原创曹则贤返朴 2021 年 12 月 06 日 08：05

本文为曹则贤著《磅礴为一》第一章。

**《磅礴为一》一书的内容简介：**本书为继《一念非凡》和《惊艳一击》之后的 “曹则贤科学教育一字系列” 第三本，书名语出庄子《逍遥游》“旁礴万物以为一”，副标题 “通才型学者的风范” 则明确了本书的主角为科学史上一些被称为 polymath 的人。本书正文十二篇，每篇介绍一位通才学者，内容包括小传、主要学术成就及其在科学史上的影响等，涉及人物有伽利略、帕斯卡、欧拉、杨、克里福德、格拉斯曼、哈密顿、勒庞、庞加莱、薛定谔、彭罗斯等。认真探讨通才型学者的教育过程、成长过程及其创造生涯，对于未来学者的培养或有些许启发意义。

本书适合具有高中以上文化各智识阶层人士阅读。

撰文***|***曹则贤（中国科学院物理研究所）

天不生仲尼，万古如长夜。

——[宋 ] 唐庾

摘要伽利略是近代科学的奠基人、近代物理的奠基人，被誉为神眷顾的数学家、托斯卡纳的阿基米德、艺术与科学的真正鉴赏者、天才的手艺人、学术自由的烈士。伽利略将有效定量化带入了物理学，用天体观测结果否定了地心说，制作了测温仪，发现了惯性定律、单摆周期公式、落体公式，以及被追认为伽利略相对论的关于运动的认识。伽利略留下了大量思想充盈、文笔优美的著作，那是物理学的启蒙典籍。

1 伽利略小传

如果不是为生活所迫，谁肯把自己弄得满身才华？我以为这句话就是个玩笑，没想到世界上还真有这样的人。意大利历史上就曾有过这么样的一个人，他被誉为 divine mathematician（神眷顾的数学家），Tuscan Archimedes（托斯卡纳的阿基米德），true connoisseur of arts and science（真正的科学与艺术鉴赏家），是第一个把有效定量化（effective quantification）引入物理学从而让物理学不再如从前那样仅仅是定性描述（qualitative description）的人，是亚里士多德学说的对头、哥白尼学说的捍卫者、数学的标准制定者、耶稣会士痛恨的人、学术自由的烈士（the sworn enemy of Aristotle，the champion of Copernicus，the standard - bearer of mathematics，the bête noire of the Jesuits，or the best - known of all martyrs to academic freedom）。这些可不是什么才华不才华的事儿，事关对人类的启蒙。这个人就是伽利略（图 1）。伽利略是个全面型的天才人物，但也是在艰难困苦中取得那些辉煌成就的。有评论称，若不是为了混口饭吃，伽利略可能不会成为这其中的任何一个角色（Galileo would have become none of these things had he not to work for a living）。

图 1. 近代科学奠基人伽利略

伽利略（Galileo Galilei，1564.02.15 - 1642.01.08），出生于意大利的比萨，祖上是佛罗伦萨国的贵族，原姓 Bonajuti。伽利略姓名的正确拼法也许应该是 Galileo de Galilei，但西方文献中用名 Galileo 和姓 Galilei 称呼他的都有。伽利略的父亲文琴佐（Vincenzo Galilei）是个天才型学者，擅长数学、音乐和音乐理论，著有《关于古代音乐与现代音乐的对话》一书。作为一个六个孩子的父亲，文琴佐没在伽利略身上花太多的时间，然而这不妨碍他的这个儿子成为近代科学的奠基人。正如薛定谔的传记作者 Walter Moore 所言，一个天才的出现首先基因必须要对（the genes must be right）。伽利略看来拥有天才的基因，思维活跃且充满智慧，小时候就善于制造各种玩具和机械模型，缺少的部分就自己发明把它补上。伽利略很早就获得了古典教育（指基于希腊语、拉丁语古典文献的教育），闲暇时光用于音乐与绘画的学习，其音乐、绘画方面的能力都是第一流的。伽利略会很多乐器，还曾想以绘画为业，其对绘画的批评为同时代人高度认同。文琴佐认识到了儿子的天分，决定支持他上大学。1580 年伽利略上了家乡的比萨大学，按照其父亲的愿望选择学医，因为当医生挣钱多。不过，伽利略很快就对数学和自然哲学产生了强烈的兴趣。1581 年，17 岁的伽利略把目光瞄向了教堂里的吊灯，窥破了单摆运动的规律。紧接着，19 岁的伽利略又开始研究阿基米德研究过的流体静力学。他写论文谈论水中的静平衡，谈论比重，这引起了前辈数学家的注意。因为伽利略一下子就搞定了这个研究，他因此被推荐给了托斯卡纳大公斐迪南一世（Ferdinand I de’ Medici，the grand duke of Tuscany）。在这位贵人的庇护下，25 岁的伽利略于 1589 年获得了在比萨大学教数学的职位，从此他的科学发现历程一发不可收。

伽利略被誉为近代科学的奠基人，近代物理学的奠基人。物理一词源于希腊文的自然（φυσις），物理学作为一门学问起源于后人安德罗尼柯（Andronicus of Rhodes，约公元前 60 年）编著的亚里斯多德（Aristotle，384 - 322 BC）的著作，与近代物理相对应的就是亚里斯多德物理学。亚里斯多德的物理、力学信条基本没有经验的支持。伽利略不是第一个挑战亚里斯多德信条的人，但他知道自己有能力给世界一个坚实的、全新的思维模式，他注定是一个理性和实验哲学新学派的奠基人。伽利略的新哲学化、智慧化方式是把每一个断言都交由实验检验，或者直接验证，或者去揭示其可能性与恰当性。伽利略把定量化表述引入了物理学，他做了一系列实验来研究亚里斯多德论断的真伪。一旦成功地证明了亚里斯多德的错误，伽利略就会公开指责，这让他从当时的学术团体收获了越来越多的反对力量。笔者以为，伽利略思考极限情形的能力、忽略细节的能力、抽象思考的能力和数学表达的能力是他成为近代科学奠基人的基本保证。

伽利略在世时即已获得先知的形象，他的声望、他著述的价值得到了同时代人的认可。自此之后，全世界任何打算教授初等物理以及刚进入物理学研究的人都应该认真研读伽利略的著作，那里是物理学和物理学研究方法、哲学的源头。伽利略著述的部分目录如下：

La bilancetta（小天平）（1586，意大利文）
De motu antiquiora（论运动之旧作）（c. 1590，拉丁文）
Le mecaniche（力学）（c.1600，意大利文）
Le operazioni del compasso geometrico et militare（测地与军用圆规实操）（1606，意大利文）
Sidereus nuncius（星信）（1610，拉丁文）
Discorso intorno alle cose che stanno in su l’acqua，o che in quella si muovono（论可浮于水面或在其中运动的物体）（1612，意大利文）
Istoria e dimostrazioni intorno alle macchie solari（太阳黑点的描述与演示）（1613，意大利文）
Discorso del flusso e reflusso del mare（论潮汐）（1616，意大利文）
Discorso delle Comete（论彗星）（1619，意大利文）
Il Saggiatore（试金者）（1623，意大利文）
Dialogo sopra i due massimi sistemi del mondo（关于两种主要世界体系的对话）（1632，意大利文）
Discorsi e Dimostrazioni Matematiche，intorno a due nuove scienze（关于两种新科学的讨论与数学论证）（1638，意大利文）
Lettera a Madama Cristina di Lorena granduchessa di Toscana（写给托斯卡纳大公夫人的信）（1615，意大利文。此书意在为哥白尼学说辩护）

意大利在 1890 - 1909 年期间出版了 Le opere di Galileo Galilei（edizione nazionale），《伽利略文集》（国家版），厚厚的二十卷。一个人的著作有国家版，也算是最高荣誉了。

2 伽利略的科学成就

伽利略是近代科学 —— 特别指物理学 —— 的奠基人，这是爱因斯坦 1954 年说的（Albert Einstein，Ideas and opinions，Crown Publishers（1954））。从伽利略留下的著作可见，伽利略为我们引入了系统的物理学研究方法，将定量化引入自然规律的表述。单摆公式、惯性定律、落体公式这些都是物理学的初步内容，也是最基础的内容，因此其内涵是要具有深厚的物理知识以后反过头来仔细品味才能体会到的。

2a）单摆的周期公式

伽利略的父亲为他在比萨大学选的是医学专业，有人调侃这是罕有的伽利略不适宜学习的专业。伽利略学医很不积极，但对学数学特别来劲儿，为此伽利略的父亲曾要求老师教数学点到为止就算了。在这段别扭的日子里（~1581 年），伽利略对比萨大学附近的大教堂里的吊灯发生了兴趣。吊灯来回晃荡（图 2），这就是后来我们初等物理课本中用单摆（pendulum，悬挂）给模型化了的现象。吊灯来回晃荡一趟所需的时间差不多（以运动在一侧的相继两次转向为准。因为空气阻力等原因，摆动幅度其实是一直在减小的，但这不妨碍认定单摆运动是周期性的。仔细想想为什么），故而猜测单摆是周期运动。伽利略发现，虽然吊灯里油的多少是变化着的，但那个固定好高度的吊灯的摆动周期是等时的（isochronous），于是得到结论：单摆的周期与摆锤（垂，pendulum）的重量无关。吊灯里的油若烧干了，就会被从教堂穹顶处放下来添油，这就有了观察一个摆长不断增加的单摆运动的机会。伽利略发现，摆绳越长，摆动周期越长。注意，那是个没有秒量级时间测量的时代（日晷只能大致划分时辰），伽利略用自己的脉搏标定吊灯晃动的周期。摆绳越长，摆动周期越长，那到底是遵循什么样的规律呢？伽利略给出的关系是周期平方同摆长成正比（注意， $y = kx^2$ 是类型的关系呃）。实际上，伽利略关于单摆研究的报告出现于 1602 年 11 月给朋友的一封信中。当然，基于现代物理知识我们知道，单摆只是在小振幅的情形下才近似地是单调振动。根据牛顿力学，摆的运动方程为 $\frac {d^2 \theta}{dt^2} + \frac {mg}{l} \sin \theta = 0$ ，其中 $m$ 是摆锤质量， $l$ 是摆绳长度， $g$ 是重力加速度（表征地球对地面上物体的吸引能力，其本质上是地球质量密度分布的反映）， $θ\theta$ 是摆绳偏离垂直方向的夹角，对于 $θ≈0\theta \approx 0$ 的情形，方程约化为 $d2θdt2+glθ=0\frac {d^2 \theta}{dt^2} + \frac {g}{l} \theta = 0$ 。此方程的解为简谐振动，周期为 $\pi \sqrt {\frac {l}{g}}$ 。

伽利略曾指导儿子据此制作摆钟，但未成功。1656 年，荷兰人惠更斯（Christiaan Huygens，1629 - 1695）做出了第一架摆钟，直到 1930 年前后摆钟都是人类最精确的时间计量设备。这是后话。

图 2. 比萨教堂里的 “伽利略的吊灯”

2b）测温仪与落体运动规律

冷热是人们熟知的自然现象，如何表述、量化冷热程度是由来已久的需求。测温仪（thermoscope，热 + 看）可看作是温度计（thermometer，热 + 量）的前身，能显示温度的变化，但未进行量化，没有具体的读数 —— 温度计有读数的前提是要有温度的标度（temperature scale），那需要热力学和别的物理学，初学热力学者应特别留意。简单的测温仪可以就是一个细长管支撑的玻璃泡，细长管的下端埋入水中。温度变化造成玻璃泡内空气气压的改变，从而造成可观察的细长管中水柱的升降。据说伽利略在 1593 年就意识到了制作测温仪的原理，1606 年跟朋友提起过他发明了测温仪。当然，测温仪所依据的气体或液体的性质（体积、压强）随温度变化的事实，古希腊时即已被认识到。实际上，测温仪在伽利略时代已经广为应用，其发明与改进是一个漫长的物理学进程，感兴趣的读者可参考专门著作，这是热力学的入门处。

但是，伽利略就是伽利略，在测温仪上他的成就可不是就定性地感知温度变化那么简单。伽利略的测温仪是个柱状密封容器，内有密度随温度变化有较明显变化的溶液（比如水加酒精以及一些脂类物质，可能由于重力和化学性质的因素还会出现不同密度物质的分层），以及几个（平均）密度不同但也在溶液密度附近的悬浮件。悬浮件是中空的玻璃泡，加上金属配重以调节其平均密度（图 3）。这样，当温度改变时，玻璃柱内液体的密度（及其分布）就会改变，相应地悬浮件的悬浮形态（哪些悬浮件会悬浮在液体中，悬浮在什么位置）就会改变，由此可以定性地判断温度的变化。然而，请记住，这里利用的是阿基米德的浮力原理，而伽利略是精研阿基米德学说的思想者。伽利略注意到（如下这段是笔者编排的，忘了在哪里读到的了），给定密度的液体，则密度比液体大的悬浮件会沉下去（初始时以加速运动的方式，距离若足够大会由于液体的粘滞力而最终变成匀速下降），密度比液体小的悬浮件保持浮在液面上，后者可以理解为下落（加）速度为零。现在，设想一开始液体的密度足够大，所有的悬浮件都浮在液面上，即下落加速度皆为零。减小液体的密度，就有一些悬浮件沉下去，但是不同步，还有一些继续浮在液面上。进一步减小液体的密度重新开始实验，则原先能沉下去的悬浮件会下落得更快些，而原先浮在液面上的某些悬浮件也能沉下去了。至少对那些刚能沉下去的悬浮件来说，它就有了得以在下落过程中追赶比它重（比它比重大）的同伴的意义了。那么，设想我们一直减小液体的密度，那就一直有密度更小的悬浮件在液体中加入了下落过程且不同比重的悬浮件之间的下落过程的差别越来越小（差别不是由液体密度造成的吗？不是有所有悬浮件的加速度都是零的初始状态的吗？）。那么，在极限情形下当液体的密度为零时，即在真空中，重物下落会是什么样的情形？唯一合理的答案是，所有的物体（管它重量是否相同、比重是否相同）在重力场中同步下落。这个结论在后来的爱因斯坦广义相对论中表现为爱因斯坦修改了惯性运动的定义：引力以外的外力为零时，物体的运动为惯性运动。

伽利略认识到了落体是同步的，与重量（质量）无关。这与亚里斯多德的物理信条相抵触，也与日常生活中未经抽象的观察不一致，如何说服同时代的人就是一件非常艰难的事儿。据说伽利略曾登上比萨的斜塔，演示不同重量的铁球是同步下落的。不过，这件轶事只见于伽利略的追随者维维安尼（Vincenzo Viviani）为伽利略所写的传记中，伽利略自己没有提及过。近代更有五花八门的验证同步下落的所谓实验，属于正经物理以外的物理探究。我愿意再次强调，不存在能验证下落同步的实验。引力场中不同重量（质量）的物体同步下落，或者在更高阶的层面上表达，纯粹引力场中物体的运动是惯性运动，得到这样的结论靠的是抽象的威力。不理解抽象的力量，物理不算入门。

此外，伽利略关于测温仪的思考还引向了热的原子论概念，此见于他 1623 年撰写的小册子 Il saggiatore （试金者）。

图 3. 伽利略的温度仪（当代复制品）

2c）惯性定律与落体运动公式

关于惯性定律的发现，伽利略在一个斜坡的对面放上另一个斜坡（图 4），他发现从左侧斜坡上滚下的小球，在对面坡上会爬上差不多同样的高度，而对面斜坡的仰角影响不大。如果将坡面弄得足够光滑，小球差不多在对面的斜坡上能达到其初始落下时所在的高度。作为理想状态（零摩擦），有理由认为小球会回复到下落时的高度，与对面斜坡的仰角无关。那么，作为极限情形，当对面斜坡的仰角为零也就是根本没有坡给小球爬升时，小球该怎么办？它努力想达到初始下落时的高度，但又一点高度也没能获得。结果呢，就是小球只能一直往前运动。于是可得到结论：受外力合力为零的物体，保持原有的运动状态不变。后来，这成了牛顿力学三定律中的第一定律，即惯性定律。是开普勒（Johannes Kepler，1571 - 1630）把物体对抗运动变化的趋势称为惯性的。请注意，质量、惯性和惯性质量完全是一回事儿（参见拙著《物理学咬文嚼字》）。

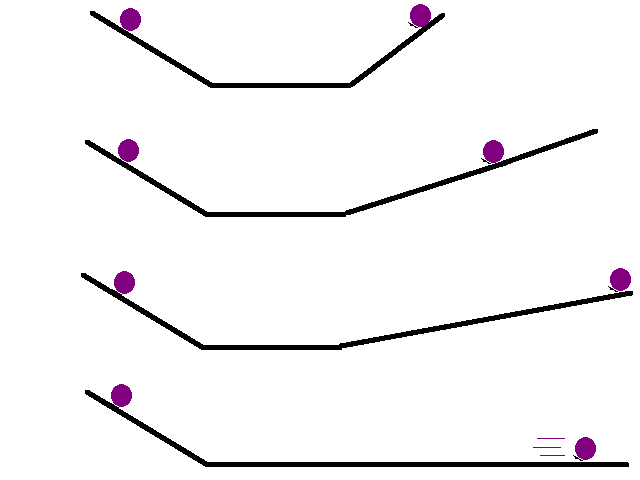
图 4. 相对的斜坡与其上小球的运动

那么，如何对落体运动加以定量地研究呢？我们知道，从 20 米的高处落下的物体，到达地面的时间大约为 2 秒，在伽利略时代，没有钟表、没有高速摄影，这可如何研究？伽利略发现，在斜坡上滚下的小球，如果斜坡的仰角足够小，下落时间就足够长，长到能进行有意义测量的程度。约在 1604 年，伽利略将一个木制斜坡的仰角做到小至 17°（图 5）。伽利略在斜坡上装上位置可调的铃铛，金属小球滚过铃铛时，会让铃铛发出响声宣告小球的经过。伽利略调节铃铛的位置，使得听到的铃铛声有（近似）相等的间隔，测量铃铛之间的间距（对于第一个铃铛，则是其到小球开始下落处的距离，开始下落处一般选为斜坡的顶端），发现间距之比约为 1:3:5:7……（此处没有精确测量。精确测量加计算机模拟，能将简单的规律都弄丢了。物理学是用头脑建立起来的）。这意思是说，随着时间单位的增加注释 [1]，小球滚过的距离为 $1^2：2^2：3^2：4^2$ …… 于是得落体定律 $\propto t^2$ 。此部分内容见于伽利略的《关于两种新科学的对话》。等到有了微积分，我们知道落体公式为 $\frac {1}{2} a t^2$ 。对于自由落体， $\frac {1}{2} g t^2$ ， $g$ 是重力加速度。注意，这里又是 $y = k x^2$ 类型的关系。实际上，法国中世纪学者奥雷斯姆（Nicole Oresme，1320~1325？-1382）此前曾得到过匀加速运动的距离 - 时间平方律。

图 5. 伽利略研究下落运动的设施

2d）望远镜与星信

前后放置的两片眼镜片有对远处物体成像的效果。1608 年，荷兰眼镜商李普希（Hans Lippershey，1570 - 1619）申请了望远镜的专利。1609 年，伽利略知道这个消息后就自己磨镜子制作了望远镜，在《星信》一书中他称之为 perspicillum，其放大倍数有 8x 和 10x 的，后来有能达到 20 x 的（图 6）。1611 年，希腊数学家 Giovanni Demisiani 基于希腊语的 τῆλε（tele，远）和 σκοπεῖν（scopein，看）造了 telescope 一词儿。利用简单的自制望远镜，伽利略宣称因此能观察到的星星比肉眼看到的多十倍都不止。伽利略完成了对月亮表面的观察，发现其上有深坑和高山并推测山的高度，观察到了木星的四颗卫星。这些都在《星信》一书中有具体的描述。Sidereus Nuncius 一书有英译本 Starry messenger，中文据此译为《星际信使》。国际上早有学者指出，正确的英译应该是 starry message—— 来自星星的消息，愚以为译成《星信》更确切些。1610 年底伽利略观察了金星的相（phase of Venus）注释 [2]，结果见于 1613 年出版的《太阳黑点的描述与演示》一书（图 7）。

图 6. 存放在佛罗伦萨伽利略博物馆的伽利略用过的望远镜

图 7. 伽利略绘制的金星的相图

伽利略的望远镜观察给西方文明带来了巨大的冲击。月球表面的坑与山的发现，说明月亮不是一个完美的球体，这与西方宗教的一大重要信仰，即天国里的星球是完美的球，星星的轨道是完美的圆，相抵触。观察到金星的相，说明金星不是绕地球转动的；而木星的四颗卫星的发现，更是说明木星也可以是转动的中心，这正应了哥白尼的日心说以及天上有许多太阳的学说。这就是说，地球不是宇宙的中心，太阳也不是宇宙的中心，宇宙中有许多看似是转动中心的地方。这些内容和西方宗教信仰起了严重冲突。

3 伽利略的对话体著作

伽利略的著述是近代科学的初始文献，对于想成为物理老师、物理学家的人们来说，其参考价值不可估量。笔者对伽利略著作的情感是相见恨晚，因见到太晚、理解太少而倍感遗憾。限于篇幅，此处仅简要介绍他的两本长篇对话体著述。

3a）关于两种主要世界体系的对话

Dialogo sopra i Due Massimi Sistemi del Mondo 一书于 1632 年用意大利语写成，这算是欧洲学术史上的大事，因为此前的学术著作是要用拉丁语写的。后来，该书于 1635 年被译成了拉丁文本，名为 Systema cosmicum（宇宙体系），英文译名为 Dialogue Concerning the Two Chief World Systems，在世界上影响甚广。本书比较此前的托勒密（Claudius Ptolemaeus，~100 - 170 AD）宇宙体系，即地心说，与新的哥白尼（Nicolaus Copernicus，1473 - 1543）宇宙体系，即日心说。此书撰写时的书名是《关于潮汐的对话》。学物理的都明白，是因为地球上水的涨落让人感知到了来自月亮的引力（场），也会引起关于地球是否运动的思考。书的结构设定为是在三个人之间分四天进行的对话的记录。三个对话主角分别名为 Salviati，一个为伽利略代言的智者；Sagredo，一个有些文化但是不持立场的人；还有 Simplicio，其是托勒密和亚里斯多德学说的拥趸，一个亚里斯多德学派或者说逍遥学派的学者（peripatetic philosopher）。这三个人各有原型，前两个姓氏来自伽利略的熟人，而第三个人的姓氏，Simplicio，按照伽利略的说法是取自著名的亚里斯多德派学者 Simplicius。但是，Simplicio 的意大利语本义就是头脑简单者的意思，讽刺之意溢于言表。Simplicio 的字面意思和在对话中的话语使得对话看似是一本攻击亚里斯多德地心说同时又为哥白尼日心说辩护的书。此书于 1632 年出版，仅仅到了 1633 年，伽利略就被教廷怀疑是异端分子因此被宗教裁判所讯问并从此被软禁，书也上了禁书目录直到 1835 年才被解禁。顺带说一句，此书不只是谈论世界体系的问题，还包括什么是好的科学啊，以及吉尔伯特（William Gilbert，1544 - 1603）**注释 [3]**的磁学研究啊，等等。

借助书中人 Salviati 之口，伽利略反驳了亚里斯多德的宇宙体系，比如他的月亮之下才有变化而月亮之外的世界没有变化的论点，论据就是观测到的 1572 年和 1604 年的新星爆发以及移动着的太阳黑子的存在。为了说明地球在运动但为什么人类却感觉不到，伽利略引入了著名的在大船舱中的力学实验 —— 此一划时代的思想实验，这就是后来于 1909 年被追认为伽利略相对论的内容（见下）。除此之外，伽利略反驳旧宇宙体系的论证还包括提供了金星的相的存在作为证据 —— 这是托勒密体系解释不了的，以及太阳黑子的移动，这可是用托勒密体系解释起来万分复杂的。实际上，金星的相，太阳黑子的存在，都是从前的宇宙理论中所没有的，若用于证明地球是静止的那肯定是错的。伽利略用潮汐来证明地球是运动着的。当然，用潮汐现象的力学去证明地球不是静止的并不正确。爱因斯坦后来就说，如果伽利略不是耍小脾气的话，也是不会认为他的论证是正确的。

《关于两种主要世界体系的对话》一书的最大价值在于产生了所谓的伽利略相对论。关于运动是相对的，伽利略的论证是一条大船虽然经过了长途跋涉我们依然能确认船上装粮食的口袋的位置，我们关切的是粮食口袋相对于船的位置，它相对于船没有运动。再者，如果大自然能让地球以外的那么大的天体都以那么大的速度推移，为啥要单单放过地球？如果将地球这个被认为唯一不动的存在从整个宇宙的图像中移去，那所谓的运动接下来会发生什么？**注释 [4]**伽利略以 “表明所有用来反对地球运动的那些实验全然无效的一个实验” 为题，详细叙述了在一个封闭船舱内发生的现象。伽利略写道：“为了最终表明实验（揭示匀速运动）的完全无效，我觉得此处正好给各位展示一个容易进行验证的途径。把你和几位朋友一起关进一艘大船甲板下的主舱里，带上几只苍蝇，几只蝴蝶，以及别的能飞的小动物。再带上一大碗水，水里有鱼；吊起一只瓶子，让里面的水滴到下面放置的广口容器中。船静止时，请仔细观察小动物在船舱里是以同样的速度四处乱飞的。鱼儿游动，无所谓是朝着哪个方向；水滴会落到正下方的容器里；朝你的朋友扔过去个什么东西，你也无需在这个方向上加把劲儿，那个方向上省点力儿，扔出去的距离都是一样的；双脚起跳，你在不同方向上会跳出去一样远。当你仔细做了这些观察（毫无疑问，船静止的时候事情就应该是这个样子的）后，让船以任何速度前行，只要速度是均匀而非忽快忽慢的。你将会看到前述效应不会有一丝儿改变，你也不能从这些观察判断出船到底是走是停。起跳，你会越过跟从前一样的距离，不会是朝着船尾跳得远而朝着船头跳得近一些儿，尽管船在高速前行，在你浮在空中的时候你脚下的船板（在你往船尾跳时）在相反的方向上一直前行。朝对面的同伴扔个什么东西，你也无需因为他是在船头或者船尾的方向而格外用力。水滴会像从前一样落到正下方的容器而不是飘向船尾，尽管下落过程中船往前窜出了一大截。碗中的鱼儿往前游和往后游一样轻松，会一样自在地游向碗边的鱼食。最后提一下，蝴蝶和苍蝇会继续四下乱飞，而不会朝船尾聚集，好像因为不得不总停留在空中跟船分离又要长途旅行而终于累了跟不上船的行程似的。再者，如果点着什么东西升起了烟，那烟会直直地升起形成一团小云彩，静止在那里，既不往前也不往后。这些（船动与静时）效应相对应的原因是，大船的运动为其所容纳之所有物体共享，包括空气。这就是为什么我说过你要呆在甲板下的原因；如果是在开放的空间中，空气就不能跟上船的行程了，则我们所说的效应多少会有些不同。无疑地，烟要比空气自身更落后一截，苍蝇，还有蝴蝶，会被空气裹挟而落后，因而若它们跟船离得远的话就跟不上船的行程。但是让它们保持靠近船，它们就能轻松地跟上；因为船，连带着它周围的空气，是一个整体。因为类似的缘故，当我们骑马的时候，会看到一些苍蝇和牛虻会老跟着我们的马，在马身上从这块儿飞到那块儿。” 伽利略在这里想要说明的一个根本思想是：“不能以任何力学实验来判断一艘船是静止还是在以任何速度匀速行驶中。” 自然可以由此推论，对于地球的运动，人们也无法觉察到。后来在 1909 年，爱因斯坦把伽利略这个思想当成（特定层面上的）相对论，称之为伽利略相对论。如果用公式表示，愚以为可作如下理解。设若宇宙的规律可用方程 $(r，t；\lambda) = 0$ 来描述，伽利略相对论要求函数 $f$ 满足如下条件：“若有 $(r，t；\lambda) = 0$ ，则对任意常数 $v$ ，必然有 $vt，t；\lambda) = 0$ 。” 伽利略时空变换为 $\rightarrow t$ ， $\rightarrow x + vt$ ， $\rightarrow y$ ， $\rightarrow z$ 。关于相对论，读者请参见拙著《相对论 - 少年版》。

3b）关于两种新科学的对话

1638 年，据说是因为青年维维安尼的上门拜师让软禁中的伽利略再次燃起了对科学的热情，他又用意大利文写成了 Discorsi e Dimostrazioni Matematiche intorno a Due Nuove Scienze 一书。该书书名的字面意思是 “关于两种新科学的讨论与数学论证”，但英译名为 Dialogue Concerning Two New Sciences，依据英译本的中译本就成了《关于两种新科学的对话》注释 [5]。这样，在英文和中文学术圈里便有了伽利略的两个对话体著作的说法。坊间流传的关于伽利略成就及思想的介绍，其中涉及这两本书中的内容就经常混淆，让人哭笑不得。

《关于两种新科学的对话》一书谈论的主题是物质结构与运动定律这两种新科学。书的结构依然是 Salviati、Sagredo 和 Simplicio 三人之间的对话，分四天进行。第一天的内容围绕固体抗（resistenza）断裂的问题。当然，学问发生的原动力多来自应用的需求，固体断裂的问题来自造船业的需求。引入注目的是书中基于对浮力的认识建议用铁造船。第二天是关于物质结合的原因的。用现代的话说，这是关于固体物理、材料力学和结构力学的学问，本书所谓的第一种新科学可理解为这几个学科的萌芽。伽利略注意到材料的抗拉能力胜过抗折能力，对相关问题亚里斯多德和阿基米德都分析过，但就严格性而言还是要数阿基米德。这一部分引起笔者注意的是，就科学方法而言，伽利略告诉我们事物既可以以脱离物质的抽象形式也可以以同事物相联系的具体形式加以考察。今天我们可以说，其实这两者都是必要的。第三天的讨论是关于运动的，包括匀速运动和自然的加速运动，第四天是关于抛体运动的。用当代的话说，这涉及运动学、动力学、引力、弹道学等内容。在伽利略之前很少有人对运动进行过真正的研究。这本书的价值在于它描述的是近代物理学的萌芽，这个对于物理学家的培养太重要了。多少对物理学和物理研究方法一无所知的人不自觉地当上了物理学家。顺便说一句，伽利略的《试金者》一书包含着更多如何做科学的思想，此书可看作伽利略的科学宣言。

4 对地动说的坚持

“E pur si mouve”，依然是它（地球）在动，是人类文明史上一句著名的格言，它被当作不畏邪恶势力坚持真理的榜样宣言。据说是在 1633 年当伽利略被要求收回地球绕太阳运动的观点时，他说了这句话。不过，这句话很可能是后人伪托的（… the motto much more likely to be apocryphal）。所谓伽利略说出过这句话一事，最早见于 1757 年意大利人 Giuseppe Baretti 的英文书 The Italian library（意大利文库）“This is the celebrated Galileo，who was in the Inquistion for six years，and put to the torture，for saying，that the Earth moved. The moment he was set at liberty，he looked up to the sky and down to the ground，and，stamping with his foot，in contemplative mood，said，Eppur si mouve注释 [6]；that is，still it moves，meaning the earth.” 而 “E pur si muove” 的确切字样是 1911 年首次在一幅据信是 1643 或者 1645 完成的、题为 Galileo in prison（狱中的伽利略）的油画中发现的（图 8）。后来，有艺术史家发现了同名的画，判断其很可能是 19 世纪的作品。但是，不管怎样，伽利略发现了地动说的诸多证据，做了详尽的分析说明，面对罗马教廷的压力依然坚持了自己的观点。伽利略开创了近代科学，为人类文明之一支带来了复兴，带来了此后以科学、技术为依托的人类文明的巨大进步。作为一个物理学者，细读伽利略的著作，笔者对他充满景仰之情。当然了，伽利略也有他的局限性。伽利略接受不了 distorted circle 的概念，自然也不接受椭圆天文学，即开普勒的行星轨道为椭圆轨道的天文学。Distorted circle，指的是椭圆（ellipsis），ellipsis 的本义就是差一点、有点儿残缺（ecliptic）。开普勒的行星运动第一、第二定律发表于 1609 年，到伽利略辞世中间有长达 33 年的时间，倘若伽利略接受了开普勒的椭圆天文学（又是耍小脾气了？），真不知道他会做出什么发现来。

图 8. Jules van Belle 所画的 “狱中的伽利略”

意大利是罗马帝国的根，国中又有超国家的宗教势力中心。就日心说而言，提出日心说的波兰人哥白尼于 1543 年去世，关于行星绕太阳运动的三大定律则是德国人开普勒分别于 1609 年（第一、第二定律）和 1619 年（第三定律）就公开发表了的，然而因为支持日心说注释 [7]，伽利略在 1632 年发表了《关于两种主要世界体系的对话》以后随即就在 1633 年被软禁了。近代物理诞生于意大利这个希腊邻居那里，有其必然性。薛定谔就曾说，什么是科学？科学就是用希腊人的方式思考。但那时的意大利无疑地也是最有能力不欢迎科学的地方，这一点想来就太有讽刺意味了。或者是很有启发意义？

5 多余的话

近年笔者在精研了一些数学物理巨擘的经历与成就之后，觉得优秀的人物首先是生就的，好的教育是第二位的。孩子的起跑线就是其出生时父母的状态，此一世他之成就所能达到的最高境界已成定局，那天花板高也罢、低也罢，就在那儿了。剩下的是他要把属于他的人生走好，而这依然是多参数的函数，有很多的偶然因素。让孩子找到他的天分所在、爱好所在，让他们过一个或轻松或紧张但都是无怨无悔的人生也许更重要。伽利略是个生来多才多艺的聪明人，但其父却能让他在大学里去选学罕有的他不适合学的学科，医学，世上也是难得有这么离谱的轶事。所幸伽利略的天才是那一点儿弯路拐不走的，瞥一眼欧几里得的《几何原本》就足以让他回到自己的使命上来。

伽利略无疑地是一位天才，其高超的思考能力、动手能力、表达能力体现在做科学和玩艺术等多个方面，这种能力显然不都是后天通过教育得到的。当然，后天的教育，来自家庭的小环境和来自社会的大环境的，对一个人的成长也是有甚至是有决定性的影响的。伽利略的著作以对话体而闻名，如果注意到伽利略的父亲文琴佐曾于 1581 年撰有 Dialogo della musica antica e della moderna （古代与现代音乐的对话），你就明白伽利略为什么爱写对话了。在那个时期，意大利的对话文本（Il dialogo）可是有传统的。

伽利略的著作是物理学的源头，它会教你怎样从头做物理研究，怎样成为一个好的物理教育工作者。笔者在 1988 年左右就买了一本意汉词典（Dizionario Italiano - Cinese），但却从没有想过要认真地去读伽利略，现在想来真是后悔。伽利略可是近代物理的奠基人啊，为什么我受的基础物理教育学中对他着墨甚少呢？这不合逻辑。

参考文献

Antonio Favaro （ed.），Le Opere di Galileo Galilei （伽利略文集），Barbera （1909）.
John Elliot Drinkwater Bethune，The Life of Galileo Galilei，Bibliobazaar （2008）.
Stillman Drake，Galileo：A very short introduction，Oxford （1980）.
Mario Livio，Galileo and the Science deniers，Simon & Schuster （2020）.
Matteo Valleriani，Galileo Engineer，Springer （2010）.
Mario Livio，Did Galileo Truly Say，“And Yet It Moves”？ A Modern Detective Story，Scientific American，May，2020

注释

[1] 时间单位就是精确的、全同的时间间隔，用整数计数。如果认为时间单位不严格相等，那前提是你有尺度更小的时间单位了。

[2] Phase，相，就是外观的意思。月球、金星从地球上看起来是什么样子当然与太阳 - 地球 - 该星体三者的相对位置有关，但是把 phase 译成相位、位相依然是个大错误！Phase 里面没有任何与位置有关的字面内容。在谈论 phase of matter，物相，phase diagram，相图，时会让人误以为这里的相与位相无关而实际上它们是一回事儿！

[3] 此位英国学者于 1600 年造了 electricus 一词。

[4] 这个走极端的、抽象的论证方式伽利略会一再用到。愚以为这是最有意义的研究方法。

[5] 如果不得不读译文，还是选择根据原文的译文才好。译文若还需经过一道转手，忠实于作者原义就更是奢望了。

[6] 一直有 “E pur si mouve” 和 “Eppur si mouve” 两种写法。

[7] 日心说也不对。笔者以为在相对论的观点下，宇宙无心处处心。

回眸 | 科学史上的巨人 —— 近代实验科学先驱者伽利略

北京科协 2024 年 02 月 15 日 16：07 北京

1564 年 2 月 15 日伽利略出生，他是意大利天文学家、物理学家和工程师。 伽利略被称为 “观测天文学之父”“现代物理学之父”“科学方法之父” 和 “现代科学之父”。他的许多成就具有开创性，为科学的进步做出了巨大的贡献，是科学史上的一位巨人。460 年后的今天，我们就来回顾他的成就。

伽利略・伽利雷（1564 年 2 月 15 日～1642 年 1 月 8 日）享年 77 岁，他是第一个使用望远镜观测天体的人。他在 1609 年发明了一种望远镜，可以放大天体的图像。这个发明使他能够观测到以前无法看到的天体，如木星的卫星和月球表面的细节。这些观测结果推翻了当时的天文学理论，证明了日心说的正确性。

伽利略发现了木星的四个卫星，这是第一个被发现的行星卫星系统。 这个发现证明了行星不一定是孤独的天体，它们可以有卫星围绕着它们旋转。这个发现也证明了日心说的正确性，因为木星的卫星不可能围绕地球旋转。

**伽利略使用望远镜观测月球，发现了月球表面的细节。**这些观测结果推翻了当时的天文学理论，证明了月球不是完美的天体，而是有地形和结构的。伽利略还观测到太阳黑子，这是太阳表面的暗斑。他的观测结果证明了太阳不是完美的天体，而是有结构和变化的。这个发现也证明了日心说的正确性，因为太阳黑子的位置和数量随着时间的推移而变化。

伽利略的结果和理论为牛顿的万有引力定律的发现奠定了基础。他的观测结果证明了天体之间存在引力作用，这个引力作用可以解释行星的运动和卫星的轨道。这个发现对牛顿的万有引力定律的发现提供了重要的预示。

**伽利略对天文学的贡献是不可估量的。**他的发现和理论推动了天文学的发展，为现代天文学的研究奠定了基础。他的成就也证明了人类的智慧和勇气，激励着我们不断探索宇宙的奥秘。

物理学成就巨大

伽利略是第一个把实验引进力学的科学家，他利用实验和数学相结合的方法确定了一些重要的力学定律。
伽利略是最早对动力学作了定量研究的人。1589 - 1591 年，他对物体的自由下落运动作了细致的观察，从实验和理论上否定了统治两千年的亚里士多德的落体运动观点。
伽利略对运动基本概念，包括重心、速度、加速度等都作了详尽研究并给出了严格的数学表达式。尤其是加速度概念的提出，在力学史上是一个里程碑。
伽利略对摆的运动作过长期的观察和研究。在后来的研究中指出单摆的周期和摆长度的平方根成反比。这一规律为后来计时机构（摆钟）的设计提供了根据。
伽利略在发现惯性定律的基础上，提出了相对性原理：力学规律在所有惯性坐标系中是等价的。力学过程对于静止的惯性系和运动的惯性系是完全相同的。

科学方法之父

十六至十七世纪由于自然科学发展的需要，要求对中世纪的研究方法进行变革。伽利略主张自然科学要坚决地同臆测的方法和神秘的观点决裂。赞成用观察、实验和数学方法相结合研究自然界，这在方法论的发展历史上意义十分重大。

古希腊和中世纪的科学家，对科学问题只是停留在定性的描述，满足于质的原因的解答。例如，物体为什么运动？是由于物体有外力推动，天体运行是由于天使推动；重物为什么会从高处落到地上，而不是飞向天空？是因为重物的天性是要回到地的中心；至于鸟要在空中飞，鱼要在水中游，都是因为鸟和鱼的本性如此。

亚里士多德物理学的这种研究方法，着重点在于探求事物的终极原因，采用的是直观的猜测，它最终只能导至神学。伽利略却相反，他不仅认为物理学原理必须来自观察和实验，并接受实践的验证；而且他还认为物理学的研究应寻求量的公理，即研究物体是怎样运动的，并用数学的公式定量地表示出物体运动的规律。这一研究方法的转变是方法论上的重大变革，“是历来关于科学方法论的最深刻、最有成效的思想”。

伽利略的研究方法直接促进了近代自然科学的发展。 他把力学与数学相结合，寻求数学公式表达运动的规律，使力学研究从猜测物体运动的原因上升为研究并证明运动的若干性质，为力学及其他科学开拓了研究的新天地。他的方法被牛顿等近代物理学大师所继承，创立了经典力学，推动了科学的发展。伽利略的研究方法同时也促进了数学的发展，由于力学和其他科学以及生产实践的需要，使数学家努力去寻求新的数学工具，微积分正是由此而产生的。所以，伽利略的科学方法论，使人们从中世纪经院式的演绎法的死胡同中摆脱出来，对创立实验科学和以后科学的发展有着深远的影响。

综编：中国科学报、“星空探秘” 公众号、果壳

函数观念的演变史：从伽利略到狄利克雷

曹亮吉
最后修改日期：2/17/2002

一、引言

文艺复兴以后，西方的科学观可以以 Galileo Galilei（1564~1642 年）的看法为代表。他认为大自然是依数学方式建构的，人只要掌握各种现象的基本数学关系，就可以靠数学加以推演。将自然科学数量化，寻求其间的数学关系并加以推演，就成了研究自然科学的新方法。科学革命对数学的影响之一就是促使函数观念渐趋成熟；当然，函数观念的成熟也使科学研究带来许多方便。

二、函数观念的早期发展

（一）Galilei 的发现

Galilei 研究落体运动，发现“物体在空中下降的距离（从静止开始计算）与所经过时间的平方成正比”、“物体从高度固定的斜板滑落所需的时间与斜板的长度成正比”。也就是说他发现了距离与时间或时间与长度之间的数学关系。距离随时间而变或时间随长度而变，用现在的说法就是：距离是时间的函数或时间是长度的函数。研究运动也引出更多的曲线──点动成曲线，而曲线和函数之间，也经由解析几何的引入，变得不可分离。

（二）解析几何与函数

用坐标的方法研究曲线，就是把曲线以 $x$ 、 $y$ 的关系式表示，然后用代数的方法加以处理。反过来，如果采取 Fermat 式的解析几何观，从任何一个 $x$ 、 $y$ 的关系式出发，探讨它所代表的曲线的几何性质，那么函数观念的重要性更显而易见了，因为 $x$ 、 $y$ 之间的关系常以函数的方法出现。

（三）初等函数的形成

函数到底是什么呢？最早的想法认为：一个函数是一个代数式子，只含变数以及加减乘除开方等符号，渐渐地，所谓超越（代数的）函数，如 $e^x$ 、 $sin⁡x\sin x$ 、 $cos⁡x\cos x$ 等等地加了进来，加上种种曲线的研究，现在所谓的初等函数，在十八世纪上半叶就已经非常清楚了。

三、函数与微积分

（一）Newton 的幂级数方法

为了求得一个函数的导数，Newton（1642~1727 年）尽量把函数写成幂级数，譬如，为了求得 $h)^\alpha$ （ $α\alpha$ 为实数）的导函数，Newton 利用的幂级数

$h)^\alpha = x^\alpha + \alpha x^{\alpha - 1} h + \text{（含有 $h$ 因数的项）}$

而得

$\alpha x^{\alpha - 1} + \text{（含有 $h$ 因数的项）}$

因此当 $h$ 趋近于 0 时，就得

$\alpha x^{\alpha - 1}$

（二）十八世纪的函数观念

到了十八世纪，数学家干脆认定函数就是幂级数。譬如

$a_0 + a_1 x + a_2 x^2 + \dots$

则

$a_1 + \text{（含有 $h$ 因数的项）}$

因此当 $h$ 趋近于 0 时，就得 $f'(x) = a_1$ 。由此可以导出：一个函数（幂级数）各项的微分和就是原函数的微分；反过来，一个函数各项的积分和就是原函数的积分。这么一来，函数的微积分变得非常简单；当然他们忽略了幂级数的收敛问题。

四、函数观念的挑战与扩展

（一）波动问题与 Euler 的观点

“函数就是幂级数”是十八世纪众所公认的观念，但波动问题的兴起，使得这种观念不时遭到挑战，迫使 Euler（1707~1783 年）也承认：最先开始时，弦所成的曲线 $y = f (x)$ 可以是任意的，只要是连续的，但不一定可以用幂级数来表示。

（二）Fourier 的三角级数

到了 Fourier（1768~1830 年）研究热传导时，他发现他必须把初期条件函数 $f (x)$ 以三角级数的方式展开：

$\frac{a_0}{2} + \sum_{n=1}^{\infty} (a_n \cos n x + b_n \sin n x)$

而

$an=1π∫−ππf(x)cos⁡nxdxa_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos n x \, dx$

$bn=1π∫−ππf(x)sin⁡nxdxb_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin n x \, dx$

根据传统的做法，他原假定 $f (x)$ 为幂级数才能得到这样的表示法，但他注意到 $a_n$ 、 $b_n$ 只不过是函数

$∫−ππf(x)cos⁡nxdx和∫−ππf(x)sin⁡nxdx\int_{-\pi}^{\pi} f(x) \cos n x \, dx \quad \text{和} \quad \int_{-\pi}^{\pi} f(x) \sin n x \, dx$

的曲线之下的面积而已，所以不管 $y = f (x)$ 是怎样的曲线， $a_n$ 、 $b_n$ 都可以计算而得。他试了种种的函数 $f (x)$ ，求取头几个 $a_n$ 、 $b_n$ 的值，发现将由此而得的三角级数头几项和所代表的曲线与原来的曲线 $y = f (x)$ 相比较，都相当接近。所以 Fourier 深信“任何”函数 $f (x)$ 都可以表成三角级数之和。

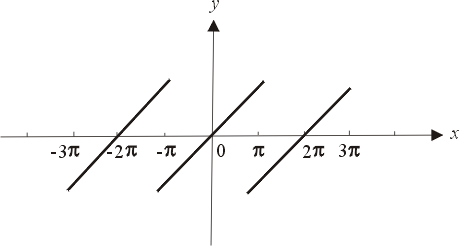
在这里插入图片描述

（三）三角级数与函数观念的再检讨

三角级数的兴起引起了函数观念的再检讨。譬如在 $y = f (x) = x$ 中，若 $x$ 在 $(−π,π)(-\pi, \pi)$ 之内，则 $f (x)$ 的三角级数表示式，因周期性的关系，会将区间内的曲线，在区间外一再重复，如图一所示。也就是说，由许多断线所组成的图形居然可以用一个级数来表示！既然如此，图一也可以当做一个函数 $g (x)$ ，虽然用简单的式子来表示时，它需要分段处理：

$y = f (x) = x,$

若 $x$ 在 $(−π,π)(-\pi, \pi)$ 之内，则

$\begin{cases} x, & \text{若 } -\pi < x < \pi \\ g(x + 2\pi), & \text{若 } x \geq \pi \\ g(x - 2\pi), & \text{若 } x \leq -\pi \end{cases}$

推而广之，可以分段用熟知的式子表示者也可以看成函数，在十八世纪时很少人会有这样的认识。

五、函数观念的澄清

（一）Dirichlet 的定义

Fourier 宣称“任何”函数都可以表成三角级数之和的看法更值得检讨，因为到底什么是函数，Fourier 也说不清楚。函数观念的澄清是 Dirichlet（1805~1859 年）研究 Fourier 论之后的重要贡献之一。他认为 $y = f (x)$ 是个函数的意思是说： $f$ 是一个规则，它告诉我们说，变数 $x$ 之值固定了，其相应唯一的 $y$ 值是什么。 $f$ 不一定要是个式子，它只要能说清楚 $x$ 到 $y$ 之间的对应是什么就好了。有了 Dirichlet 的函数观念，数学家才能谈什么时候 $a_n$ 、 $b_n$ 之值可以确定，什么相对应的三角级数在特定的区间内和原来的函数是一致的。

（二）函数的表示方法

虽然 Dirichlet 有了函数最一般的定义，通常我们总希望用式子来表示一个函数所提供的规则。但什么是式子呢？譬如，我们都承认 $f(x) = x^2 + x + 1$ 是个式子；其实它代表一段叙述，告诉我们函数对应的规则：把变数 $x$ 自乘，加上变数本身，再加上 1，就是变数对应的 $y$ 值。只因我们太习惯多项式所代表的意义，所以认为它是个式子，而不认为它代表的是一段叙述。再如 $\sqrt{x}$ 也是一样，初学的人认为它代表一段叙述，但习焉不察后就成了式子。 $f (x) = [x]$ 代表不超过 $x$ 的最大整数，更是一个明显的例子。除了多项式、幂级数、三角级数外，更一般的函数项级数，譬如以 Bessel 函数或 Legendre 多项式为通项的级数，都可以看成式子。

（三）“暗”式子与“明”式子

除了“明”的式子外，还有些“暗”的式子。“暗”的式子指的是以参数函数、隐函数、微分方程式、积分方程式等来表示自变数 $x$ 与他变数 $y$ 之间的数学关系。怎样化暗为明自然是最重要的课题之一。

六、函数的几何表示

（一）函数与曲线

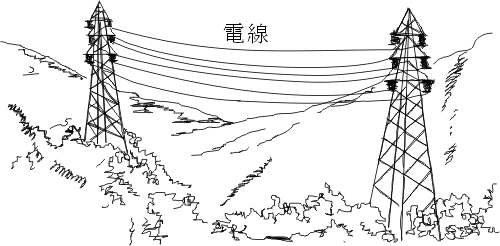
式子之外，函数最常以曲线的形式出现。当然，每当有曲线出现，数学家总是想办法把它量化，以式子的形式表示，好方便研究。譬如行星运行的轨道，是个椭圆，其（隐）函数为 $x2a2+y2b2=1\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ 。譬如两电线杆之间的电线所成的曲线（见图二），称为悬垂线。我们发现物理的观点，坐标之间的关系可以用微分方程式表示；解了此方程式，就得悬垂线的函数为
$\frac{a(e^{x/a} + e^{-x/a})}{2}$

双曲余弦函数与悬链线方程

一、函数表达式的关联与转化

给定函数 $\frac{a(e^{x/a} + e^{-x/a})}{2}$ ，其本质是双曲余弦函数的变形形式，具体转化逻辑如下：

1. 双曲余弦函数（ $cosh⁡(x)\cosh(x)$ ）

双曲函数是一类与三角函数（如正弦、余弦）性质相似，但基于双曲线而非圆定义的数学函数。其中，双曲余弦函数定义式为：
$cosh⁡(x)=ex+e−x2\cosh(x) = \frac{e^x + e^{-x}}{2}$

“h”是“hyperbolic”（双曲的）的缩写。

2. 变量替换推导等价形式

对双曲余弦函数的自变量进行替换，令自变量为 $xa\frac{x}{a}$ （ $a$ 为常数），将其代入核心定义式，可得：
$cosh⁡(xa)=ex/a+e−x/a2\cosh\left(\frac{x}{a}\right) = \frac{e^{x/a} + e^{-x/a}}{2}$

3. 关联原函数

将上述替换后的式子两边同时乘以常数 $a$ ，即可与给定函数 $ y = \frac{a(e^{x/a} + e^{-x/a})}{2} $ 完全对应，得到等价形式：
$\cosh\left(\frac{x}{a}\right)$

二、常数 $a$ 对函数图像的影响

常数 $a$ 是函数的尺度因子（scaling factor），直接决定函数图像的形状，具体通过“垂直伸缩”和“水平伸缩”双向影响：

1. 垂直方向影响（振幅/高度）

$a$ 作为双曲余弦函数 $cosh⁡(xa)\cosh\left(\frac{x}{a}\right)$ 前面的系数，控制图像在垂直方向的拉伸或压缩：

当 $a$ 增大时：函数曲线在垂直方向被拉伸，整体更“高”或更“深”；
当 $a$ 减小时：函数曲线在垂直方向被压缩，整体更“扁平”或更“浅”。

2. 水平方向影响（宽度）

$a$ 位于自变量 $x$ 的分母（即 $xa\frac{x}{a}$ ）中，控制图像在水平方向的拉伸或压缩：

当 $a$ 增大时：函数曲线在水平方向被拉伸，整体更“宽”；
当 $a$ 减小时：函数曲线在水平方向被压缩，整体更“窄”。

三、函数的实际物理意义：悬链线模型

函数 $\cosh\left(\frac{x}{a}\right)$ 是物理学中悬链线（catenary） 的精准数学表达式，可描述无外力干扰时，柔性物体在重力单独作用下形成的自然弯曲形状，典型场景包括：

悬挂的电缆、高压电线；
自然下垂的链条、绳索；
桥梁设计中柔性承重结构的弯曲形态。

（二）复杂曲线与函数表示

又譬如小提琴声波呈现规则而复杂的形状（见图三），它可以表成一三角级数。

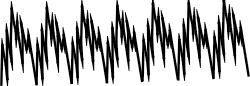
在这里插入图片描述

当然并不是每条曲线都能找到适当的式子。譬如某地的气温变化曲线，患病者的脑波（见图四）等等这些太不规则的曲线恐怕就很难用式子表示。

在这里插入图片描述

（三）特殊函数与图形表示

Dirichlet 曾经考虑过有理数的特征函数，它在有理数时取值为 1，否则为 0。这样的函数根本无法用图形来表示。

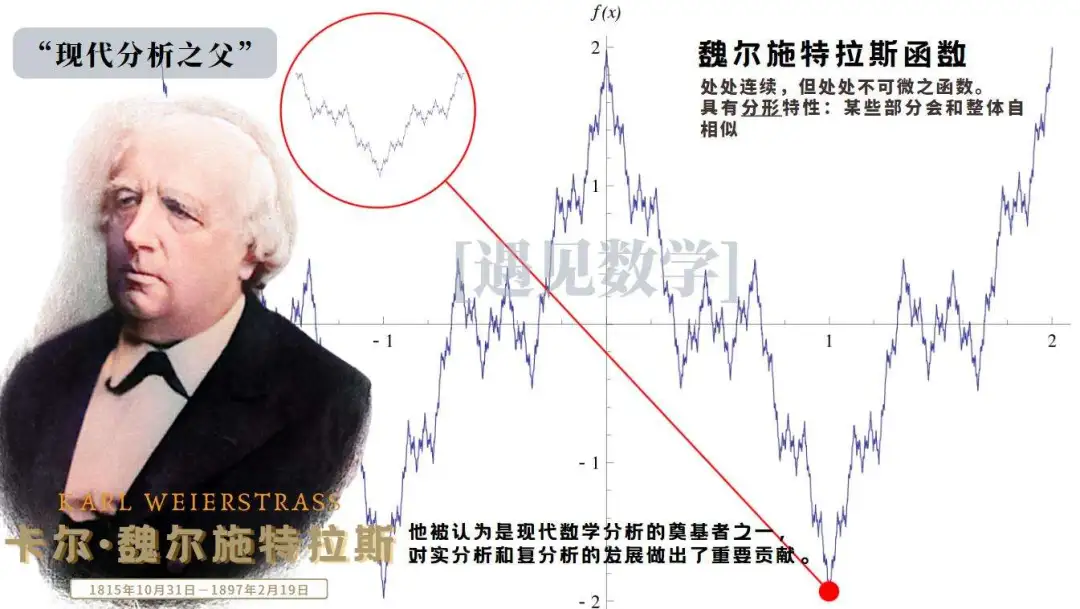
Weierstrass（1815~1897 年）曾经提出一个级数函数

$\sum_{n=0}^{\infty} b^n \cos(a^n \pi x), \quad a \text{ 为奇数}, \ 0 < b < 1, \ ab > 1 + \frac{3}{2} \pi$

在这里插入图片描述

[遇见数学] 配图

它是个连续的，但到处不可微分的函数。用曲线的观点来看，它是个连续不断，一整条的，但又到处没有切线的曲线。这样的曲线是用图画不出来的。别以为这是古怪的曲线，Wiener（1894~1964 年）证明：几乎所有的分子的 Brown 运动的路径都是连续而到处没有切线的。

七、函数观念的总结

Dirichlet 的函数观不但包含已往种种的函数，提供了许许多多新鲜有趣、有用的例子，而且也因为函数观念的确定，使得数学家能够讨论函数的连续、微分、积分等种种有关的性质。经过几世纪的发展，函数成为数学中最基本的观念之一，同时也是科学数量化的主要工具。

八、注释

Leibniz 在 1673 年首先提到函数（function）这个字眼，他指的是跟随一曲线上的点而变动的量，譬如切线长、法线长、次切线、纵坐标等等。 $f (x)$ 作为一般函数的符号是 1734 年 Euler 首先采用的。

via:

伽利略是如何奠定近代科学的？| 贤说八道
https://mp.weixin.qq.com/s/SVzUFf7lVMrDXTx8_qWhbw
回眸 | 科学史上的巨人 —— 近代实验科学先驱者伽利略
https://mp.weixin.qq.com/s/w_noHj5xB9DdsyoedAtpKA
函数观念的演变史 - 曹亮吉
https://episte.math.ntu.edu.tw/articles/sm/sm_15_12_1/index.html
函数观念的演变史：从伽利略到狄利克雷，函数观念怎么一步步变成今天这样的？
https://mp.weixin.qq.com/s/Z69Rw9R3AgL5iAemxzj_3Q

查看全文

http://www.dtcms.com/a/418363.html