线性代数（标量与向量+矩阵与张量+矩阵求导）

标量与向量

import numpy as np#定义向量
x = np.array([2,5,8])
print(x)
print(x.shape)#向量转置
print(x.T)
print(x.t.shape)y = np.array([1,3,7])
# 向量相乘  [2,15,56]
print(x * y)# 向量点乘，或者np.dot(x,y)    73
print(x.dot(y))# python3.5之后用@符号
print(x @ y)

#计算范数
l0_norm = np.linalg.norm(x,ord=0) #3.0l1_norm = np.linalg.norm(x,ord=1) # 15.0l2_norm = np.linalg.norm(x,ord=2) #

矩阵与张量

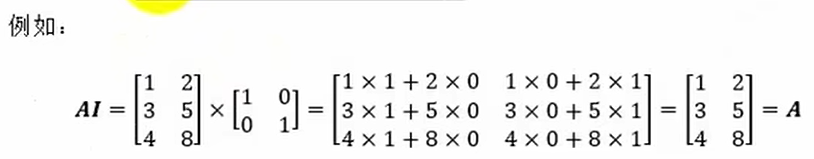
import numpy as npA = np.array([[1,2,3],[4,5,6]])
B = np.array([[1,3,7],[5,0,2]])print(A)
print(A.shape)#矩阵与矩阵相乘（对应位置元素相乘，哈达玛积）
print(A * B)#矩阵乘法
print(A.dot(B))
print(A.dot(B.T))print(A @ B.T)# 求逆
C = np.array([[1,2],[3,5]])
C_inv = np.linalg.inv(C)print(C.dot(C_inv))
print(C_inv.dot(C))
C_inv = np.around(C_inv).astype(int)# 向量化
print(A.flatten())# 矩阵内积
print("<A,B> = ",np.sum(A*B))
print("<A,B> = ",np.dot(A.flatten(),B.flatten()))#克罗内克积
print(np.kron(A,B))

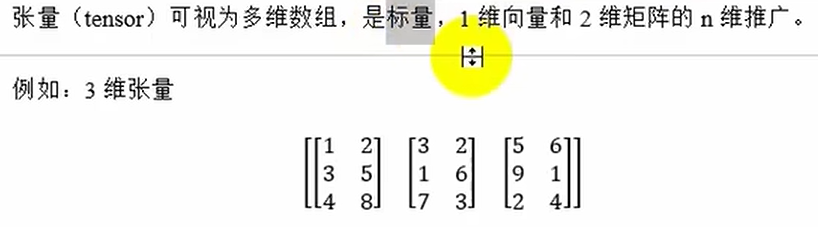
# 定义张量
tensor = np.array([[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]])
print(tensor)
print(tensor.shape) #两个矩阵，每个矩阵是2*3

矩阵求导

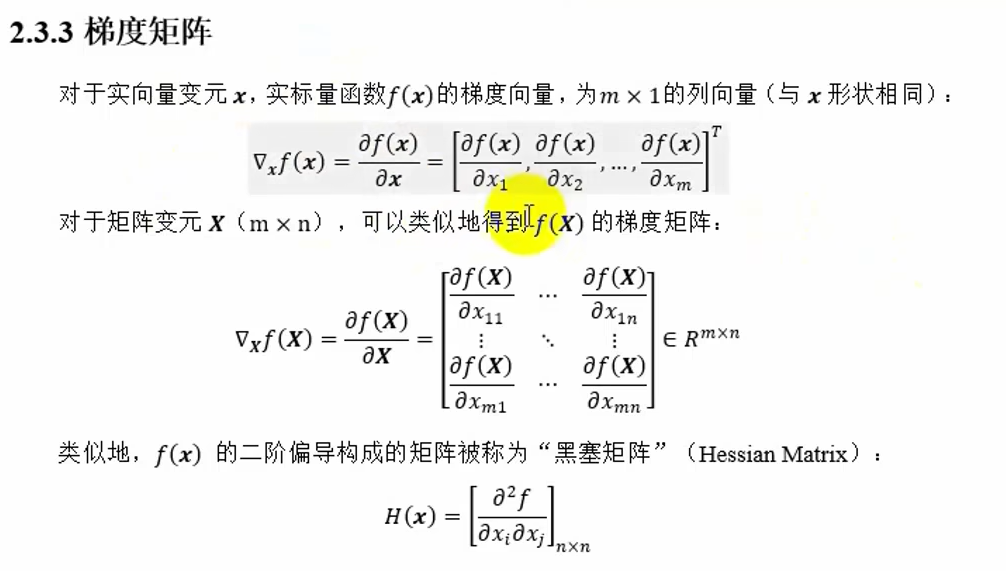
#计算梯度
f = np.array([1,2,4,7,11,16])
np.gradient(f)