Per-Tensor 量化和Per-Channel 量化
1️⃣ 基本概念
量化的目标
量化(Quantization)是将浮点数权重或激活映射到整数表示,从而降低模型存储和计算成本。
量化公式通常为:
q=round(rs) q = \text{round}\left(\frac{r}{s}\right) q=round(sr)
其中:
- rrr 是浮点数权重或激活
- qqq 是整数表示
- sss 是 scale(缩放因子)
- 对于 非对称量化,还有 zero-point zzz:
q=round(rs)+z q = \text{round}\left(\frac{r}{s}\right) + z q=round(sr)+z
Per-Tensor 量化
- 定义:整个张量使用一个统一的 scale(和 zero-point)进行量化。
- 公式(对称量化为例):
s=max(∣W∣)2b−1−1 s = \frac{\max(|W|)}{2^{b-1}-1} s=2b−1−1max(∣W∣)
其中:
- WWW 是权重张量
- bbb 是量化位宽(比如 8-bit)
特点:
- 只用一个 scale,简单高效
- 对 所有通道 使用相同 scale
- 对权重差异较大的通道,会出现精度损失
Per-Channel 量化
- 定义:对张量的每个输出通道(通常是卷积的 out_channels 或 Linear 的 out_features)使用独立的 scale(和 zero-point)进行量化。
- 公式(对称量化):对每个通道 ccc:
sc=max(∣Wc∣)2b−1−1 s_c = \frac{\max(|W_c|)}{2^{b-1}-1} sc=2b−1−1max(∣Wc∣)
特点:
- 每个通道的 scale 不同,更精细,能够保留不同通道权重的动态范围
- 更高精度,尤其是卷积网络里通道差异大时
- 实现稍复杂,需要在推理时对每个通道单独反量化
2️⃣ 举例对比
假设有一个 4×3 的卷积权重:
W=[0.10.2−0.13.0−2.51.20.050.1−0.05−1.00.50.2] W = \begin{bmatrix} 0.1 & 0.2 & -0.1 \\ 3.0 & -2.5 & 1.2 \\ 0.05 & 0.1 & -0.05 \\ -1.0 & 0.5 & 0.2 \end{bmatrix} W=0.13.00.05−1.00.2−2.50.10.5−0.11.2−0.050.2
-
Per-Tensor 量化:
- 找整个张量最大绝对值:3.0
- scale = 3.0 / 127 ≈ 0.0236
- 所有元素都用这个 scale 量化 → 小数值会损失较多精度
-
Per-Channel 量化(按行/通道量化):
- 通道 1 max=3.0 → s1=0.0236
- 通道 2 max=2.5 → s2≈0.0197
- 通道 3 max=1.2 → s3≈0.00945
- 每个通道单独量化 → 精度更高
3️⃣ 优缺点对比
| 特性 | Per-Tensor | Per-Channel |
|---|---|---|
| 精度 | 较低(通道动态范围不同损失大) | 较高 |
| 实现复杂度 | 简单 | 复杂(每通道独立 scale) |
| 存储开销 | 少(一个 scale) | 多(每个通道一个 scale) |
| 常用场景 | 激活量化(A8)、小模型 | 权重量化(W8)、大模型 |
4️⃣ PyTorch 示例
import torch
import torch.nn as nn
import torch.quantization as tq# 假设线性层权重
weight = torch.tensor([[0.1, 0.2, -0.1],[3.0, -2.5, 1.2],[0.05, 0.1, -0.05],[-1.0, 0.5, 0.2]])# Per-Tensor 量化
scale = torch.max(weight.abs()) / 127
q_weight_tensor = torch.round(weight / scale)
print("Per-Tensor Quantized:\n", q_weight_tensor)# Per-Channel 量化 (按行)
scales = torch.max(weight.abs(), dim=1)[0] / 127
q_weight_channel = torch.round(weight / scales[:, None])
print("Per-Channel Quantized:\n", q_weight_channel)
✅ 总结
- Per-Tensor:简单、快速,但精度可能低
- Per-Channel:复杂、存储略多,但精度更高,特别适合权重量化
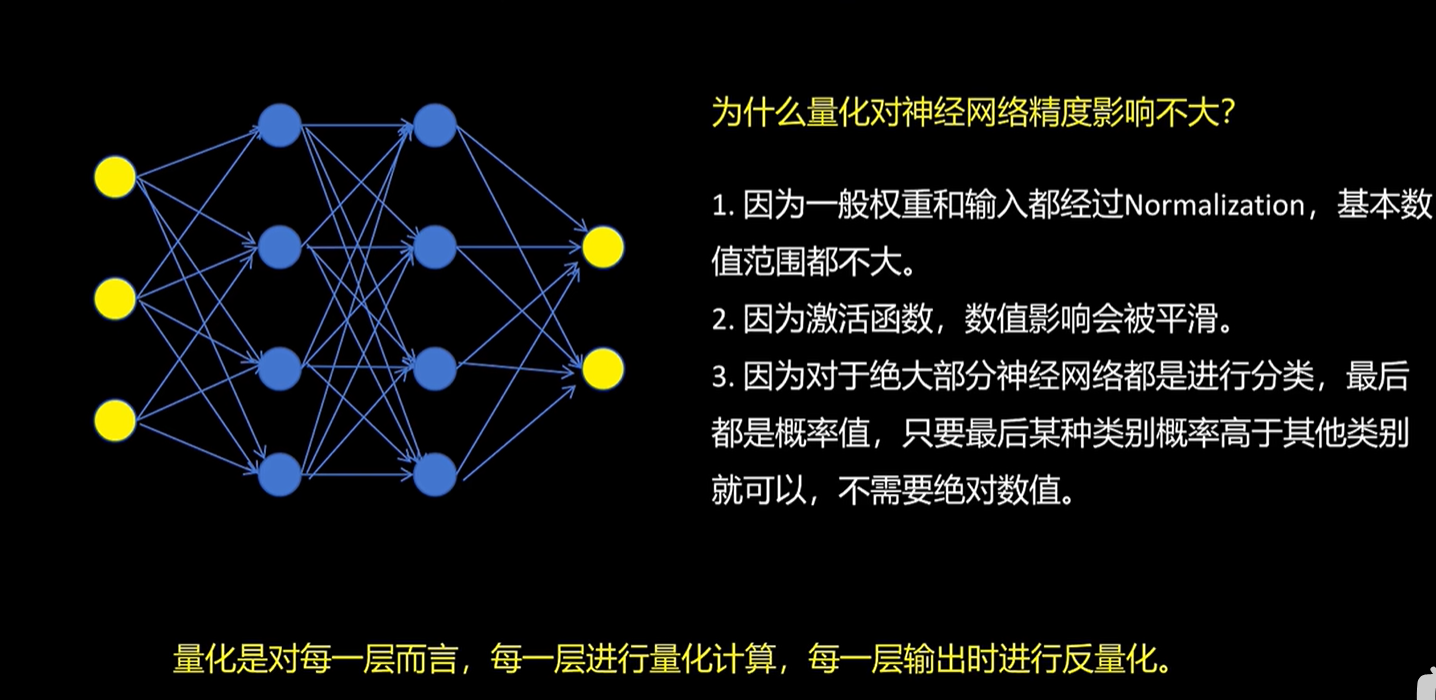
2 为什么量化对神经网络精度影响不大?