当前位置：首页 > news >正文

现代循环神经网络

news 2025/9/22 10:57:30

门控循环单元（GRU）

门控隐状态

重置门和更新门

候选隐状态

隐状态

从零开始实现

长短期记忆网络（LSTM）

输入门、忘记门和输出门

候选记忆元

记忆元

从零开始实现

门控循环单元（GRU）

RNN计算梯度时遇到的问题：当进行矩阵连续乘积时，可能会导致梯度消失（梯度变得非常小，无法有效更新模型参数）或梯度爆炸（梯度变得非常大，导致模型不稳定）。

三种情况下，这种梯度异常可能带来的意义或影响：

长期依赖问题： 早期观测值对预测未来观测值非常重要（例如，序列末尾的校验和），但如果缺乏记忆机制，早期信息的影响会随着时间推移而减弱，导致模型无法捕捉长期依赖关系。
无关观测值的干扰： 序列中可能包含与预测目标无关的观测值（例如，网页情感分析中的HTML代码），我们希望模型能够忽略这些无关信息。
序列内部状态的重置需求： 序列中可能存在逻辑中断或过渡（例如，书籍章节的过渡），此时我们可能需要一种机制来重置模型的内部状态。

解决方案：长短期记忆（LSTM）和门控循环单元（GRU）

为了解决上述问题，学术界提出了许多方法。其中最早且广泛使用的是**长短期记忆（LSTM）**模型，由 Hochreiter and Schmidhuber 在1997年提出。
门控循环单元（gated recurrent unit, GRU），由 Cho et al. 在2014年提出。
GRU被描述为LSTM的一个稍微简化的变体，它能够提供与LSTM同样的效果，但在计算上速度更快（因为它参数更少，结构更简单）。

门控隐状态

门控循环单元与普通的循环神经网络之间的关键区别在于：前者支持隐状态的门控。这意味着模型有专门的机制来确定应该何时更新隐状态，以及应该何时重置隐状态。这些机制是可学习的，并且能够解决了上面列出的问题。例如，如果第一个词元非常重要，模型将学会在第一次观测之后不更新隐状态。同样，模型也可以学会跳过不相关的临时观测。最后，模型还将学会在需要的时候重置隐状态。

重置门和更新门

重置门（reset gate）：这个门决定了我们应该“忘记”过去的隐藏状态的多少。它允许模型选择性地忽略掉一部分旧的信息。
更新门（update gate）：这个门决定了有多少旧的隐藏状态信息需要保留，以及有多少新的隐藏状态信息需要加入。

计算公式

在给定的时间步 $t$ ，模型接收一个大小为 $N \times d$ 的小批量输入 $\mathbf{X}_t$ (其中 $N$ 是样本数， $d$ 是输入特征数)。
前一个时间步的隐藏状态是 $\mathbf{H}_{t-1}$ ，其维度为 $N \times h$ (其中 $h$ 是隐藏单元的数量)。

重置门： $R_t = \sigma\left( X_t W_{xr} + H_{t-1} W_{hr} + b_r \right)$

更新门： $Z_t = \sigma\left( X_t W_{xz} + H_{t-1} W_{hz} + b_z \right)$

$\mathbf{W}_{xr}$ 和 $\mathbf{W}_{xz}$ 是权重参数，维度为 $d \times h$ 。
$\mathbf{W}_{hr}$ 和 $\mathbf{W}_{hz}$ 也是权重参数，维度为 $h \times h$ 。
$\mathbf{b}_r$ 和 $\mathbf{b}_z$ 是偏置参数，维度为 $1 \times h$ 。

候选隐状态

在门控循环单元（GRU）中，候选隐状态 $\tilde{H}_t$ 是对传统RNN隐状态更新机制的一种改进，它引入了重置门（Reset Gate） $R_t$ 来控制过去隐状态对当前候选状态的影响。

计算公式

$\tilde{H}_t = \tanh(X_t W_{xh} + (R_t \odot H_{t-1}) W_{hh} + b_h)$

参数说明：

$X_t$ : 当前时间步的输入向量

$H_{t-1}$ : 上一时间步的隐状态

$R_t$ : 重置门向量，元素值在 $(0, 1)$ 之间

$\odot$ : Hadamard积（按元素相乘）

$W_{xh} \in \mathbb{R}^{d \times h}$ : 输入到候选状态的权重矩阵

$W_{hh} \in \mathbb{R}^{h \times h}$ : 隐状态到候选状态的权重矩阵

$b_h \in \mathbb{R}^{1 \times h}$ : 偏置项 $\tanh$ : 激活函数，将输出压缩到 $(-1, 1)$ 区间

重置门的作用

当 Rt 接近 1 时：表示“保留”过去的信息，候选状态类似于标准RNN的更新方式。
当 Rt 接近 0 时：表示“忽略”过去的信息，候选状态主要依赖于当前输入 Xt，相当于“重置”了隐状态。

候选隐状态是GRU中用于平衡历史信息与当前输入的关键机制。通过重置门，模型可以灵活地决定是否使用过去的隐状态来生成新的候选状态，从而增强模型对长期依赖关系的建模能力。

隐状态

在门控循环单元（GRU）中，候选隐状态 $\tilde{H}_t$ 只是中间结果，最终的隐状态 $H_t$ 是由 更新门 $Z_t$ 控制下的 旧隐状态 $H_{t-1}$ 与 候选隐状态 $\tilde{H}_t$ 的凸组合（加权平均）决定的。

最终隐状态更新公式：

$H_t = Z_t \odot H_{t-1} + (1 - Z_t) \odot \tilde{H}_t$

符号说明：

$Z_t \in (0, 1)$ ：更新门向量，元素值越接近1表示越“保留”旧状态

$\odot$ ：Hadamard积（按元素相乘）

$H_{t-1}$ ：上一时间步的隐状态

$\tilde{H}_t$ ：当前时间步的候选隐状态（由重置门和输入决定）

更新门的作用

更新门值	行为	含义
$Z_t \approx 1$	$H_t \approx H_{t-1}$	几乎不更新，保留旧状态，忽略当前输入
$Z_t \approx 0$	$H_t \approx \tilde{H}_t$	完全更新，新状态由当前输入和候选状态决定

设计意义

缓解梯度消失：如果整个子序列的更新门都接近1，旧状态可以被长期保留，从而跨越多个时间步传递信息。
捕捉长期依赖：更新门允许模型选择性遗忘或保留历史信息，有助于建模长距离依赖。
与重置门分工：
- 重置门（Reset Gate）→ 控制短期依赖（是否忽略最近的状态）
- 更新门（Update Gate）→ 控制长期依赖（是否保留遥远的历史）

从零开始实现

import torch
from torch import nn
from d2l import torch as d2lbatch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
def get_params(vocab_size, num_hiddens, device):num_inputs = num_outputs = vocab_sizedef normal(shape):return torch.randn(size=shape, device=device)*0.01def three():return (normal((num_inputs, num_hiddens)),normal((num_hiddens, num_hiddens)),torch.zeros(num_hiddens, device=device))W_xz, W_hz, b_z = three()  # 更新门参数W_xr, W_hr, b_r = three()  # 重置门参数W_xh, W_hh, b_h = three()  # 候选隐状态参数# 输出层参数W_hq = normal((num_hiddens, num_outputs))b_q = torch.zeros(num_outputs, device=device)# 附加梯度params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q]for param in params:param.requires_grad_(True)return params
def init_gru_state(batch_size, num_hiddens, device):return (torch.zeros((batch_size, num_hiddens), device=device), )
def gru(inputs, state, params):W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = paramsH, = stateoutputs = []for X in inputs:Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)H = Z * H + (1 - Z) * H_tildaY = H @ W_hq + b_qoutputs.append(Y)return torch.cat(outputs, dim=0), (H,)
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_params,init_gru_state, gru)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

1. 数据加载

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

batch_size=32：每次喂给网络 32 条序列。
num_steps=35：每条序列长度 35 个字符。
返回值
- train_iter：无穷迭代器，每次产生 (X, Y) 形状都是 (32,35)，X 是输入字符索引，Y 是偏移 1 位的目标字符索引。
- vocab：d2l.Vocab 对象，能把字符↔索引互转。

2. 参数初始化 get_params

def get_params(vocab_size, num_hiddens, device):
num_inputs = num_outputs = vocab_size # 输入/输出维度都是词表大小
def normal(shape):
return torch.randn(size=shape, device=device)*0.01 # 高斯初始化
def three():
# 3 个共享初始化方式的矩阵/向量
return (normal((num_inputs, num_hiddens)),
normal((num_hiddens, num_hiddens)),
torch.zeros(num_hiddens, device=device))

GRU 需要 3 组门/状态 的权重，每组 3 个张量：

输入→门/状态 (vocab_size, num_hiddens)
隐状态→门/状态 (num_hiddens, num_hiddens)
偏置 (num_hiddens,)

W_xz, W_hz, b_z = three() # 更新门 Z W_xr, W_hr, b_r = three() # 重置门 R W_xh, W_hh, b_h = three() # 候选隐状态 ˜H

输出层：

W_hq = normal((num_hiddens, num_outputs)) # 隐状态→输出
b_q = torch.zeros(num_outputs, device=device)

把所有参数收进列表并打开梯度：

params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q]
for param in params:
param.requires_grad_(True)
return params

3. 隐状态初始化 init_gru_state

def init_gru_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device), )

返回元组 (H,)，方便与 LSTM 等状态兼容（LSTM 有 (H,C)）。
初始隐状态全 0，形状 (batch_size, num_hiddens)。

4. 核心：一步 GRU 计算 gru

def gru(inputs, state, params):
# 拆包
W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []

inputs 是列表，长度=num_steps，每个元素形状 (batch_size, vocab_size)（one-hot 向量）。
遍历时间步：

for X in inputs: # X: (batch, vocab_size)
Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z) # 更新门
R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r) # 重置门
H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h) # 候选状态
H = Z * H + (1 - Z) * H_tilda # 最终隐状态
Y = H @ W_hq + b_q # 输出 logits
outputs.append(Y)
return torch.cat(outputs, dim=0), (H,)

把 num_steps 个 (batch, vocab_size) 的 Y 在 dim=0 上拼起来 → (num_steps*batch, vocab_size)，正好与 Y_true 的形状对应。

5. 组装模型并训练

vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(
vocab_size, num_hiddens, device,
get_params, init_gru_state, gru)

d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

d2l.RNNModelScratch 是 d2l 提供的通用训练壳，它会把：
- 你给的 get_params / init_gru_state / gru 组装成 forward；
- 自动做 softmax 交叉熵损失；
- 做 梯度裁剪、** perplexity 计算**、采样生成文本。

训练 500 个 epoch，学习率 1。
每 epoch 打印困惑度（perplexity）+ 采样 50 个字符检验效果。

简洁实现

num_inputs = vocab_size
gru_layer = nn.GRU(num_inputs, num_hiddens)
model = d2l.RNNModel(gru_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

高级API包含了前文介绍的所有配置细节，所以我们可以直接实例化门控循环单元模型。这段代码的运行速度要快得多，因为它使用的是编译好的运算符而不是Python来处理之前阐述的许多细节。

长短期记忆网络（LSTM）

LSTM 的灵感来源于 计算机逻辑门。
引入 记忆元（memory cell），用于记录附加信息，帮助网络更好地捕捉长期依赖。
记忆元与隐状态形状相同，但功能不同：隐状态负责短期输出，记忆元负责长期存储。

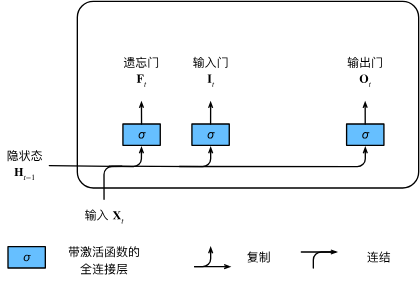
输入门、忘记门和输出门

门的名称	作用	符号
遗忘门（Forget Gate）	决定丢弃记忆元中的哪些信息	$F_t$
输入门（Input Gate）	决定哪些新信息存入记忆元	$I_t$
输出门（Output Gate）	决定记忆元中哪些信息用于当前输出	$O_t$

长短期记忆网络的数学表达:

输入： $X_t \in \mathbb{R}^{n \times d}$

上一隐状态： $H_{t-1} \in \mathbb{R}^{n \times h}$

则三个门的计算方式为：

$I_t = \sigma(X_t W_{xi} + H_{t-1} W_{hi} + b_i)$

$F_t = \sigma(X_t W_{xf} + H_{t-1} W_{hf} + b_f)$

$O_t = \sigma(X_t W_{xo} + H_{t-1} W_{ho} + b_o)$

其中：

$\sigma$ 是 Sigmoid 激活函数

$W$ 是权重矩阵， $b$ 是偏置项

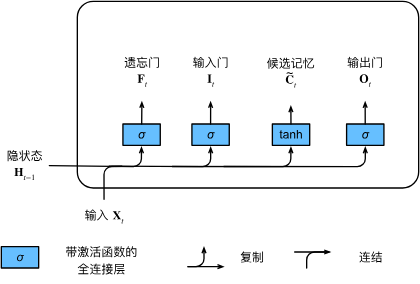
候选记忆元

作用

提供新的候选信息，供输入门筛选后更新到记忆元中。
类似 GRU 中的候选隐状态，但 LSTM 额外用输入门控制其写入比例。

计算方式

$\tilde{C}_t = \tanh(X_t W_{xc} + H_{t-1} W_{hc} + b_c)$

激活函数： $tanh$ ，输出区间 $\left ( -1,1 \right )$ 。

参数：

$W_{xc}\in\mathbb R^{d\times h}$ ：输入→候选记忆
$W_{hc}\in\mathbb R^{h\times h}$ ：上一隐状态→候选记忆
$b_c\in\mathbb R^{1\times h}$ ：偏置

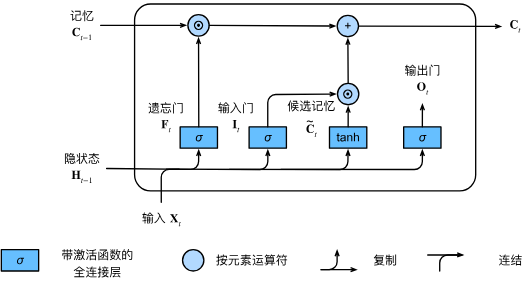
记忆元

作用

长期记忆容器 Ct：跨时间步保存信息，缓解梯度消失。
由 遗忘门 Ft 和 输入门 It 共同控制“旧记忆保留多少”与“新候选写入多少”。

更新公式

$C_t = F_t \odot C_{t-1} + I_t \odot \tilde{C}_t$

$\odot$ ：Hadamard 积（按元素乘）。

$\tilde{C}_t$ ：候选记忆元（tanh 输出，范围 −1~1）。

$F_t, I_t \in (0,1)$ ：分别决定旧记忆衰减程度与新信息写入程度。

极端情况直观

若 $F_t=1, I_t=0$ → $C_t = C_{t-1}$ ：完全保留旧记忆，不写入新信息。
若 $F_t=0, I_t=1$ → $C_t = \tilde{C}_t$ ：彻底重写记忆。

从零开始实现

import torch
from torch import nn
from d2l import torch as d2lbatch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
def get_lstm_params(vocab_size, num_hiddens, device):num_inputs = num_outputs = vocab_sizedef normal(shape):return torch.randn(size=shape, device=device)*0.01def three():return (normal((num_inputs, num_hiddens)),normal((num_hiddens, num_hiddens)),torch.zeros(num_hiddens, device=device))W_xi, W_hi, b_i = three()  # 输入门参数W_xf, W_hf, b_f = three()  # 遗忘门参数W_xo, W_ho, b_o = three()  # 输出门参数W_xc, W_hc, b_c = three()  # 候选记忆元参数# 输出层参数W_hq = normal((num_hiddens, num_outputs))b_q = torch.zeros(num_outputs, device=device)# 附加梯度params = [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc,b_c, W_hq, b_q]for param in params:param.requires_grad_(True)return params
def init_lstm_state(batch_size, num_hiddens, device):return (torch.zeros((batch_size, num_hiddens), device=device),torch.zeros((batch_size, num_hiddens), device=device))
def lstm(inputs, state, params):[W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,W_hq, b_q] = params(H, C) = stateoutputs = []for X in inputs:I = torch.sigmoid((X @ W_xi) + (H @ W_hi) + b_i)F = torch.sigmoid((X @ W_xf) + (H @ W_hf) + b_f)O = torch.sigmoid((X @ W_xo) + (H @ W_ho) + b_o)C_tilda = torch.tanh((X @ W_xc) + (H @ W_hc) + b_c)C = F * C + I * C_tildaH = O * torch.tanh(C)Y = (H @ W_hq) + b_qoutputs.append(Y)return torch.cat(outputs, dim=0), (H, C)
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_lstm_params,init_lstm_state, lstm)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

数据加载（与 GRU 代码完全一样）

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

每次喂 32 条序列，每条 35 个字符。
train_iter 永不停歇地产生 (X, Y)：
- X：(batch, 35) 字符索引
- Y：(batch, 35) 目标索引（X 整体右移 1 位）

参数初始化 get_lstm_params

def three(): # 工厂函数：返回 (W_x, W_h, b)
return (normal((num_inputs, num_hiddens)),
normal((num_hiddens, num_hiddens)),
torch.zeros(num_hiddens, device=device))

W_xi, W_hi, b_i = three() # 输入门
W_xf, W_hf, b_f = three() # 遗忘门
W_xo, W_ho, b_o = three() # 输出门
W_xc, W_hc, b_c = three() # 候选记忆
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)

LSTM 比 GRU 多一个门 + 一个候选记忆元，所以一共 4 组权重，每组 3 个张量。

门/状态	权重矩阵 1	权重矩阵 2	偏置	作用
输入门 $I_t$	$W_{xi}$	$W_{hi}$	$b_i$	控制写入多少新信息
遗忘门 $F_t$	$W_{xf}$	$W_{hf}$	$b_f$	控制丢弃多少旧记忆
输出门 $O_t$	$W_{xo}$	$W_{ho}$	$b_o$	控制记忆多少用于输出
候选记忆 $\widetilde{C_t}$	$W_{xc}$	$W_{hc}$	$b_c$	生成新的候选记忆
输出层	$W_{hp}$	—	$b_q$	隐状态 → 字符 logits

最后把所有参数收进列表并打开梯度：

params = [W_xi, W_hi, b_i, ..., W_hq, b_q]
for p in params:
p.requires_grad_(True)

状态初始化 init_lstm_state

LSTM 的“状态”是一个元组：

H：隐状态 (batch, num_hiddens) → 用于当前输出
C：记忆元 (batch, num_hiddens) → 用于长期记忆

return (torch.zeros((batch_size, num_hiddens), device=device),
torch.zeros((batch_size, num_hiddens), device=device))

手写 LSTM 前向传播 lstm

def lstm(inputs, state, params):
[W_xi, W_hi, b_i, ..., b_q] = params
H, C = state
outputs = []
for X in inputs: # 逐个时间步处理，X: (batch, vocab_size)

4 个门的计算（全部向量ized，batch 并行）

I = torch.sigmoid(X @ W_xi + H @ W_hi + b_i) # 输入门
F = torch.sigmoid(X @ W_xf + H @ W_hf + b_f) # 遗忘门
O = torch.sigmoid(X @ W_xo + H @ W_ho + b_o) # 输出门
C_tilda = torch.tanh(X @ W_xc + H @ W_hc + b_c) # 候选记忆

记忆元更新

C = F * C + I * C_tilda # (9.2.3) 元素级

隐状态更新

H = O * torch.tanh(C) # 先压缩记忆再按输出门 masking

输出 logits

Y = H @ W_hq + b_q # (batch, vocab_size)
outputs.append(Y)

返回形状

return torch.cat(outputs, dim=0), (H, C)

outputs 列表里每个 Y 形状 (batch, vocab)，共 num_steps 个。
torch.cat 后在 dim=0 拼接 → (num_steps * batch, vocab)，正好与 Y_true 扁平后的形状一致。

组装模型 & 训练

vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device,
get_lstm_params, init_lstm_state, lstm)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

RNNModelScratch 负责：
- 调 get_lstm_params 初始化参数
- 每个 epoch 调 lstm 做前向 + 反向
- 自动算交叉熵、梯度裁剪、采样生成文本
训练 500 epoch，学习率 1，GPU 上几分钟即可看到困惑度降到 < 50。

简洁实现

num_inputs = vocab_size

lstm_layer = nn.LSTM(num_inputs, num_hiddens)

model = d2l.RNNModel(lstm_layer, len(vocab))

model = model.to(device)

d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

查看全文

http://www.dtcms.com/a/394326.html