深入浅出现代FPU浮点乘法器设计
在通用处理器(CPU)和图形处理器(GPU)的核心深处,浮点运算单元(FPU)扮演着执行科学计算、图形渲染和人工智能任务的基石角色。而浮点乘法器,作为FPU中最复杂且最关键的部件,其设计哲学完美体现了计算机架构在速度、精度、面积和功耗之间的精妙权衡。今天,我们就来揭开现代浮点乘法器的设计奥秘。
1. 浮点乘法的核心步骤
一个标准的浮点乘法 并非一次简单的计算,而是一条精心设计的流水线:
异常与操作数检查:计算伊始,硬件便并行检查输入是否为 NaN、无穷大或零。若为特殊值,则直接根据IEEE 754规则输出结果,绕过所有复杂计算,极大提升效率。
指数相加:计算
。这一步使用常规整数加法器即可完成,并会同时进行溢出与下溢检测。
尾数相乘:这是整个过程的性能核心,也是设计难度最高的部分。两个有效位数(如24位)相乘,需要处理高达48位的中间结果。
结果规范化:乘积必须调整回
的标准格式。这由前导零计数器(LZC) 和高速桶形移位器协同完成,后者能在单周期内完成任意位数的移位。
舍入处理:根据IEEE 754的舍入模式,检查最低有效位、保护位和粘位,决定是否进位。此步骤可能导致结果再次溢出,从而触发二次规范化。
符号计算:最简单的一步,一个异或门(XOR)并行计算出结果的符号位
。
上述所有步骤被精细地划分为多个流水级,使得每个时钟周期都能开始一个新的乘法操作,从而实现极高的吞吐率。
2. 灵魂所在:尾数乘法的硬件实现艺术
尾数相乘绝非简单的"移位-相加",它由两大核心技术协同完成:Booth编码负责减少工作量,压缩树负责高效执行。让我们深入探究这两个关键模块的细节。
2.1. Booth编码:化繁为简的智慧
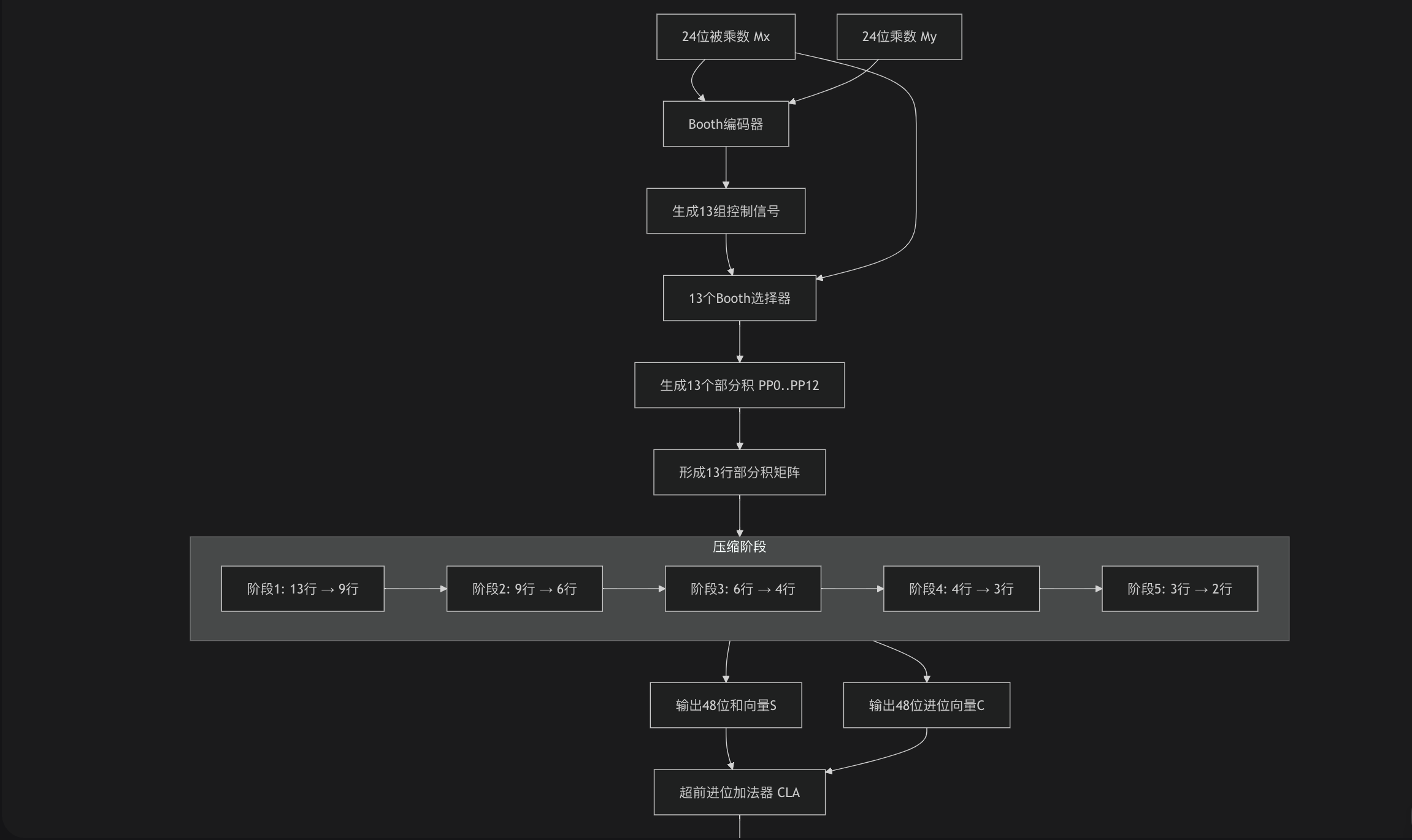
Booth编码的核心突破在于它重新定义了乘法过程。传统的移位-相加方法需要生成n个部分积(n为乘数位宽),而改进的基4 Booth编码通过每次处理2个乘数位,将部分积数量直接减半。
编码原理深度解析
基4 Booth编码基于一个关键的数学观察:任何二进制数都可以用一组有符号的数字来表示。编码器每次扫描乘数的3个连续位(重叠1位),根据其数值产生相应的操作控制信号。
编码规则如下表所示,其中 为乘数的三个连续位:
| 操作 | 数学意义 | |||
|---|---|---|---|---|
| 0 | 0 | 0 | 加 0 | |
| 0 | 0 | 1 | 加 1倍被乘数 | |
| 0 | 1 | 0 | 加 1倍被乘数 | |
| 0 | 1 | 1 | 加 2倍被乘数 | |
| 1 | 0 | 0 | 减 2倍被乘数 | |
| 1 | 0 | 1 | 减 1倍被乘数 | |
| 1 | 1 | 0 | 减 1倍被乘数 | |
| 1 | 1 | 1 | 减 0 |
硬件实现细节
每个Booth编码单元由两部分组成:
编码逻辑 简单的组合逻辑电路,实现上述真值表
部分积生成器 基于编码结果的多路选择器,能够输出5种可能结果之一
对于负操作(-X, -2X),硬件采用二进制补码实现:先产生正数的部分积,然后取反并在最低有效位添加补偿的"1"。这个补偿位会在部分积矩阵的适当位置进行处理。
24位乘法通过Booth编码后,部分积从24个减少到13个,压缩比接近50%,为后续处理节省了大量硬件资源。
2.2. Dadda树:极致高效的压缩引擎
Dadda乘法器是一种高度优化的压缩树结构,其目标是用最少数量的加法器将部分积矩阵压缩到只剩两行。
压缩策略与阶段规划
Dadda树的压缩过程遵循一个预定义的"Dadda数列"(2, 3, 4, 6, 9, 13, 19, 28...)。每个压缩阶段的目标高度就是这个数列中的下一个数值。
以13个部分积为例,压缩过程分为几个明确的阶段:
从13行压缩至9行
从9行压缩至6行
从6行压缩至4行
从4行压缩至3行
从3行压缩至2行
基本构建模块
Dadda树使用两种基本元件:
全加器(FA):将3个输入位压缩为1个和位(sum)和1个进位位(carry)
半加器(HA):将2个输入位压缩为1个和位和1个进位位
全加器的布尔表达式为:
布局与布线优化
Dadda树的真正优势在于其硬件布局的规整性。与Wallace树相比,Dadda树在每一阶段只进行必要的压缩,这使得:
加法器之间的互连更短更规整
布线拥塞程度更低
时序更容易满足
总体面积更小
这种规整性在现代纳米级工艺中尤为重要,因为互连延迟往往比门延迟更加关键。
最终相加阶段
经过Dadda树压缩后,得到两个48位的向量:和向量与进位向量。这两个向量通过一个超前进位加法器(CLA)进行最终相加。CLA采用并行计算所有进位的算法,避免了行波进位加法器的线性延迟,确保了高速运算。
为了更直观地理解Booth编码与Dadda树的协同工作流程,下图展示了24位尾数相乘的完整数据路径:

3. 现代设计趋势与优化
融合乘加(FMA)一统天下 现代FPU几乎不再设计独立的乘法器,而是直接设计乘加融合单元来计算 。FMA 只需一次舍入和规范化,而非两次,因此在速度、精度和能效上都碾压传统的"先乘后加"操作,已成为绝对主流。
SIMD与子字并行 在SIMD单元(如AVX、NEON)中,一个宽乘法器被拆分为多个并行的窄乘法器。例如,一个256位宽的FMA单元可以同时执行8个32位单精度浮点乘加运算。
先进的功耗管理:
门控时钟 在单元空闲时切断时钟信号,消除动态功耗。
操作数隔离 阻止无效数据在乘法器阵列中传播,减少不必要的电路翻转。
4. 整体总结
现代浮点乘法器的设计是一场贯穿多个层次的协同优化:
算法层面,通过Booth编码减少计算复杂度。
电路层面,通过Dadda树和超前进位加法器实现高效压缩和快速求和。
架构层面,通过流水线、FMA和SIMD最大化吞吐率和能效。
系统层面,通过智能的功耗管理技术降低能耗。
