动态规划算法的欢乐密码(六):子数组系列(下)



专栏:算法的魔法世界
个人主页:手握风云
目录
一、例题讲解
1.1. 等差数列划分
1.2. 最长湍流子数组
1.3. 单词拆分
1.4. 环绕字符串中唯一的子字符串
一、例题讲解
1.1. 等差数列划分

给定一个整数数组 nums,返回数组中所有为等差数列的子数组个数。 等差数列是指一个数列中,任意两个相邻元素之间的差值都相等。
根据题目要求,本题的状态表示为以i位置为结尾,所有子数组的中有多少个等差数列。如下图所示,如果a1、a2、a3、a4能构成等差数列,同时a3、a4、a5也能构成等差数列,那么我们很容易得出a1、a2、a3、a4、a5也能构成等差数列。
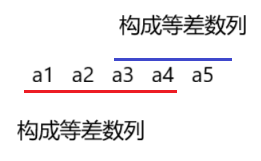
要想构成等差数列,至少是3个元素。如果nums[i]与nums[i-1],nums[i-2]能构成等差数列,那么以nums[i]为结尾的等差子数组,是在以nums[i - 1]结尾的等差子数组的基础上,再额外追加上nums[i],dp[i]=dp[i-1]+1。如果nums[i]与nums[i-1],nums[i-2]不能构成等差数列,那么前面有多少等差子数组也没用,dp[i]=0。
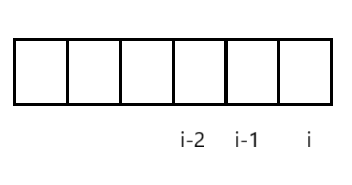
初始化的时候,以nums[0]和nums[1]为结尾,都无法构成等差子数组,所以dp[0]与dp[1]初始化为0。填表顺序,从左到右。返回值,我们需要所有等差子数组的数量,所以我们需要遍历dp表求和再返回。
完整代码实现:
class Solution {public int numberOfArithmeticSlices(int[] nums) {int n = nums.length, ret = 0;// 数组长度小于3,无法形成等差数列if (n < 3) {return 0;}int[] dp = new int[n];for (int i = 2; i < n; i++) {// 如果当前元素与前两个元素构成等差数列if (nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2]) {dp[i] = dp[i - 1] + 1;}}// 计算所有等差数列的数量for (int i : dp) {ret += i;}return ret;}
}1.2. 最长湍流子数组

给定一个整数数组 arr,我们需要找到一个最长的子数组,这个子数组被称为"湍流子数组"。湍流子数组的定义是: 1. 对于子数组中的所有相邻元素对,它们的符号交替变化。具体来说: • 如果 arr[i] > arr[i+1],那么下一个比较应该是 arr[i+1] < arr[i+2] • 如果 arr[i] < arr[i+1],那么下一个比较应该是 arr[i+1] > arr[i+2]。
根据题目要求,本题的状态表示为:以i位置为结尾最长湍流子数组的长度。当我们以arr[i]为结尾时,需要与arr[i-1]进行比较,此时可以分为3种情况:arr[i]>arr[i-1]、arr[i]>arr[i-1]、arr[i]==arr[i-1]。那么我们的状态表示可以继续细分:f[i]表示以i位置元素为结尾的所有子数组中,最后呈现“上升"状态下的最长湍流数组的长度;g[i]表示以i位置元素为结尾的所有子数组中,最后呈现“下降”状态下的最长湍流数组的长度。
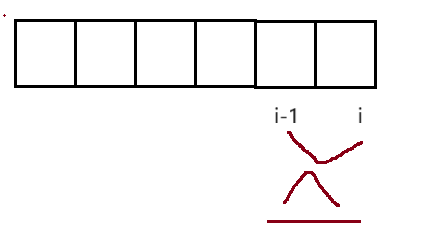
当arr[i]<=arr[i-1]时,那么只能最后一个元素构成子数组,f[i]=1;当arr[i]>arr[i-1]时,那么就是前面下降状态的最长湍流数组再加上nums[i]本身(g[i-1]),f[i]=g[i-1]+1。同理,当arr[i]>=arr[i-1]时,g[i]=1;当arr[i]<arr[i-1]时,g[i]=f[i-1]+1。
初始化:因为单独一个元素也可以构成湍流子数组,所以两个表都可以初始化为1,并且还能简化填表。填表顺序从左到右两个表同时填写。返回值:两个表里面的最大值。
完整代码实现:
class Solution {public int maxTurbulenceSize(int[] arr) {int n = arr.length, ret = 0;if (n == 1) {return 1;}int[] f = new int[n];int[] g = new int[n];for (int i = 0; i < n; i++) {f[i] = g[i] = 1;}for (int i = 1; i < n; i++) {if (arr[i] > arr[i - 1]) {f[i] = g[i - 1] + 1;} else if (arr[i] < arr[i - 1]) {g[i] = f[i - 1] + 1;}ret = Math.max(ret, Math.max(f[i], g[i]));}return ret;}
}1.3. 单词拆分

给定一个仅由小写英文字母组成的字符串s,以及一个同样由小写英文字母组成、且所有字符串互不相同的单词列表wordDict。判断字符串s能否通过拼接wordDict中的一个或多个单词得到。
根据题目要求,本题的状态表示为[0, i]区间内的字符串能否被字典内的单词拼接而成,就意味着我们的dp表要创建成一个boolean类型的。动态规划根据前一步划分问题,以[j, i]为索引的单词是否存在于字典wordDict中,s的区间[0, j - 1]是否能被字典内的单词拼接而成,那么dp[i]才能被拼接成,所以状态转移方程为dp[i]=dp[j-1]&&wordDict.contains。初始化的时候,我们在前面加一个虚拟头节点,当j=0时,如果s存在于wordDict中,当dp[0]=true时,dp[1]=true。字符串在映射时,我们可以在s前面添加一个","或者"_"来保证映射关系正确。填表顺序,从左到右。返回值,返回dp表最后一个值。
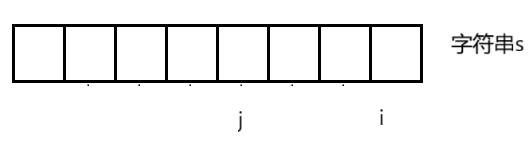
完整代码实现:
class Solution {public boolean wordBreak(String s, List<String> wordDict) {int n = s.length();boolean[] dp = new boolean[n + 1];dp[0] = true;// 将字符串s前面加上一个逗号,方便处理s = "," + s;for (int i = 1; i <= n; i++) {for (int j = i; j >= 1; j--) {if (dp[j - 1] && wordDict.contains(s.substring(j, i + 1))) {// 如果s[1,j-1]可以被拆分,并且s[j,i]在字典中,则s[1,i]可以被拆分dp[i] = true;break;}}}return dp[n];}
}1.4. 环绕字符串中唯一的子字符串

存在一个无限环绕的字符串base,由小写字母abcdefghijklmnopqrstuvwxyz循环组成,给定一个小写字母字符串s,统计并返回 s 中有多少不同非空子串也在 base 中出现。
根据题目要求,本题的状态表示为以i位置为结尾的所有子串中,有多少个在base中出现。当子串长度为1,也就是以自身一个字符为子串,那么dp[i]=1(此时一定存在于base中);当子串长度大于1,s.substring(0, i-1)也存在于base中,如果再加上最后一个字符也能存在于base中,那么dp[i]=dp[i-1]+1。初始化的时候,因为一个字符也能存在于base中,所以我们dp里面的值都初始化为1。填表顺序,从左往右。返回值需要注意,在示例2中出现了两个重复子串"c",所以我们还要进行去重。相同字符结尾的dp值取最大,我们可以使用大小为26的哈希数组来保存字符结尾最大的dp值。
完整代码实现:
class Solution {public int findSubstringInWraproundString(String s) {int n = s.length();int[] dp = new int[n];for (int i = 0; i < n; i++) {dp[i] = 1;}for (int i = 1; i < n; i++) {// 判断当前字符串是否与前一个相邻if (s.charAt(i - 1) + 1 == s.charAt(i) || (s.charAt(i - 1) == 'z' && s.charAt(i) == 'a')) {// 如果相邻,则当前字符串的长度加1dp[i] += dp[i - 1];}}char[] arr = s.toCharArray();int[] hash = new int[26];int ret = 0;// dp[i]表示以第i个字符结尾的字符串的最大长度for (int i = 0; i < n; i++) {hash[arr[i] - 'a'] = Math.max(hash[arr[i] - 'a'], dp[i]);}for (int i : hash) {ret += i;}return ret;}
}