当前位置：首页 > news >正文

因果推断DAGs和控制变量：如何使用有向无环图选择因果推断的控制变量

news 2025/9/22 13:04:24

文章目录

0 笔者笔记
1 有向无环图
- 1.1 定义
- 1.2 因果关系
2 示例：班级规模与数学成绩
3 结论
4 参考文献
- 代码

0 笔者笔记

当我们想弄清楚一件事（原因）是否真的导致了另一件事（结果）时，比如“多看广告（原因）会不会让用户更活跃（结果）”，这比我们想象的要复杂。很多时候，我们看到的“相关性”可能只是巧合，或者背后有其他因素在作怪。

这篇文章【DAGs and Control Variables】介绍了一种叫**有向无环图（DAGs）**的工具，它就像一张“因果关系地图”，能帮我们理清这些复杂的联系。

DAGs怎么用？

变量：图上的每个点代表一个因素（比如“广告数量”、“用户活跃度”）。
箭头：箭头表示因果关系，比如 $\to 用户活跃度$ 表示广告数量影响用户活跃度。
路径：从一个变量到另一个变量的连接线。

关键在于区分两种路径：

因果路径：箭头方向一致，表示真正的因果链条。
虚假路径：箭头方向不一致，看起来有关系，但实际上不是直接的因果。

我们最怕的两种情况是：

混淆变量（Confounder）：想象一个因素 $Z$ ，它同时影响 $X$ 和 $Y$ 。比如，“用户活跃度高低（ $Z$ ）”可能导致“看到更多广告（ $X$ ）”，也可能导致“更愿意互动（ $Y$ ）”。如果我们不把“用户活跃度”这个因素考虑进去，就会错误地认为“看更多广告”直接导致了“更愿意互动”。DAGs告诉我们，要控制这种混淆变量，才能得到真实的因果关系。控制它就像把这条虚假路径“堵住”。
对撞点（Collider）：这是最反直觉的。想象一个因素 $Z$ ，它同时被 $X$ 和 $Y$ 影响。比如，“用户抱怨广告多（ $Z$ ）”可能因为“看到了很多广告（ $X$ ）”，也可能因为“本来就对平台不满意，活跃度低（ $Y$ ）”。通常情况下， $X$ 和 $Y$ 通过 $Z$ 看起来没关系。但如果你控制了对撞点 $Z$ （比如，只分析那些抱怨广告多的用户），反而会人为地在 $X$ 和 $Y$ 之间制造出一种虚假关联。这就像把一条本来“堵住”的虚假路径“打开”了。

核心原则：
为了准确找出 $X$ 对 $Y$ 的真实影响，我们应该：

控制那些可能同时影响 $X$ 和 $Y$ 的混淆变量，以消除虚假关联。
避免控制那些同时被 $X$ 和 $Y$ 影响的对撞点，因为这反而会引入新的虚假关联。

应用例子：
假设某电商平台想知道“给用户发放优惠券（ $X$ ）”是否能真正提高“用户购买转化率（ $Y$ ）”。

混淆变量的例子：用户的“购物需求强度（ $Z$ ）”。购物需求强的用户（ $Z$ ）可能更容易收到优惠券（ $X$ ），也更容易购买（ $Y$ ）。如果不控制“购物需求强度”，平台可能会高估优惠券的效果。这里，我们需要控制 $Z$ 。
对撞点的例子：用户的“客服咨询频率（ $Z$ ）”。用户“收到优惠券（ $X$ ）”可能会因为优惠券规则复杂而增加咨询频率（ $Z$ ）。同时，用户“购买转化率低（ $Y$ ）”也可能因为遇到问题而增加咨询频率（ $Z$ ）。在这种情况下，“客服咨询频率”就是对撞点。如果你只分析那些“咨询过客服的用户”，你可能会发现“优惠券”和“购买转化率”之间出现一种奇怪的、不真实的关联。所以，这里我们不应该控制 $Z$ 。

通过DAGs，我们可以更清晰地识别这些变量，避免在数据分析中得出错误的因果结论，从而做出更明智的决策。

1 有向无环图

在分析因果关系时，很难理解应该以哪些变量为条件进行分析，即如何“拆分”数据，以便我们进行同类比较。例如，如果你想了解拥有平板电脑对学生表现的影响，那么比较学生社会经济背景相似的学校是有意义的。否则，风险在于只有富裕学生才能负担得起平板电脑，如果不加以控制，我们可能会将这种影响归因于平板电脑，而不是社会经济背景。

当感兴趣的处理来自一个适当的随机实验时，我们不需要担心以其他变量为条件。如果平板电脑在学校之间随机分发，并且我们在实验中有足够的学校，我们就不必担心学生的社会经济背景。以某些所谓的“控制变量”为条件进行分析的唯一优势可能是提高统计功效。然而，这是另一个话题。

在这篇文章中，我们将简要介绍有向无环图（DAGs），以及它们如何有助于选择用于因果分析的条件变量。DAGs 不仅提供了关于我们需要在分析中包含哪些变量的视觉直觉，还指出了我们应该不包含哪些变量以及原因。

1.1 定义

有向无环图（DAGs）提供了数据生成过程的视觉表示。随机变量用字母表示（例如 [X]），因果关系用箭头表示（例如 →）。例如，我们将其解释为

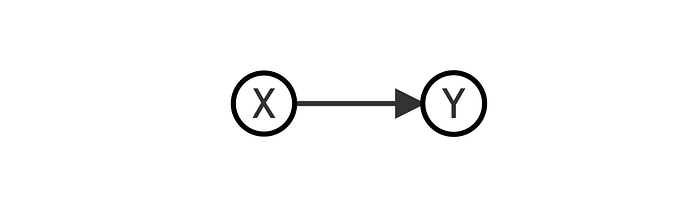
[X]（可能）导致 [Y]。我们称路径为两个变量 [X] 和 [Y] 之间的任何连接，独立于箭头的方向。如果所有箭头都指向前方，我们称之为因果路径；否则，我们称之为虚假路径。

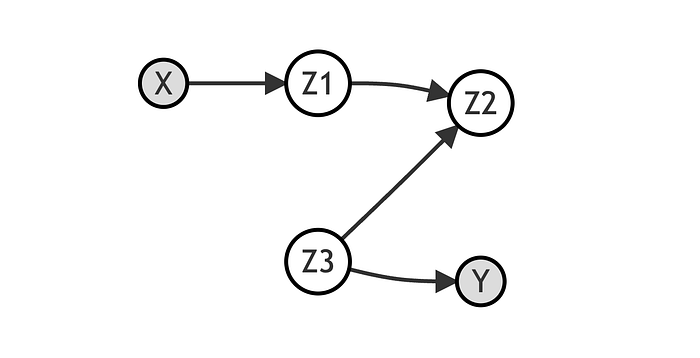
在上面的例子中，[X] 和 [Y] 之间存在一条通过变量 [Z_1]、[Z_2] 和 [Z_3] 的路径。由于并非所有箭头都指向前方，这条路径是虚假的，并且 [X] 对 [Y] 没有因果关系。事实上，变量 [Z_2] 是由 [Z_1] 和 [Z_3] 共同引起的，因此阻断了这条路径。

[Z_2] 被称为对撞点（collider）。

我们分析的目的是评估两个变量 [X] 和 [Y] 之间的因果关系。有向无环图很有用，因为它们为我们提供了关于我们需要以哪些其他变量 [Z] 为条件进行分析的指导。以一个变量为条件进行分析意味着我们将其固定，并在其他条件不变的情况下得出结论。例如，在线性回归框架中，插入另一个回归变量 [Z] 意味着我们正在计算在给定 [X] 的情况下，[Y] 的条件期望函数的最佳线性近似，以 [Z] 的观测值为条件。

1.2 因果关系

为了评估因果关系，我们希望关闭 [X] 和 [Y] 之间的所有虚假路径。现在的问题是：

路径何时开放？如果它不包含对撞点，则开放。否则，它就是关闭的。
如何关闭开放路径？你需要以至少一个中间变量为条件。
如何打开关闭路径？你需要以路径上所有对撞点为条件。

假设我们再次对 [X] 对 [Y] 的因果关系感兴趣。让我们考虑以下图：

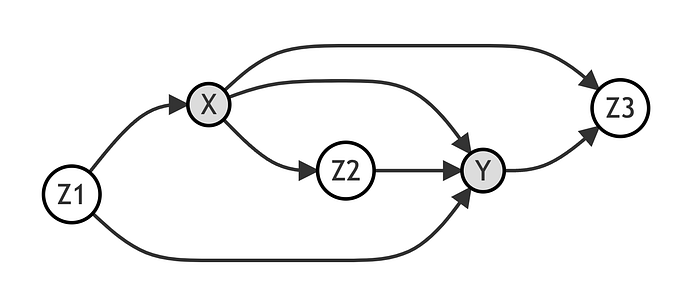
在这种情况下，除了直接路径之外，[X] 和 [Y] 之间还存在三条非直接路径，它们通过变量 [Z_1]、[Z_2] 和 [Z_3]。

让我们考虑在分析 [X] 和 [Y] 之间的关系时，忽略所有其他变量的情况。

通过 [Z_1] 的路径是开放的，但它是虚假的。
通过 [Z_2] 的路径是开放的，并且是因果的。
通过 [Z_3] 的路径是关闭的，因为 [Z_3] 是一个对撞点，并且它是虚假的。

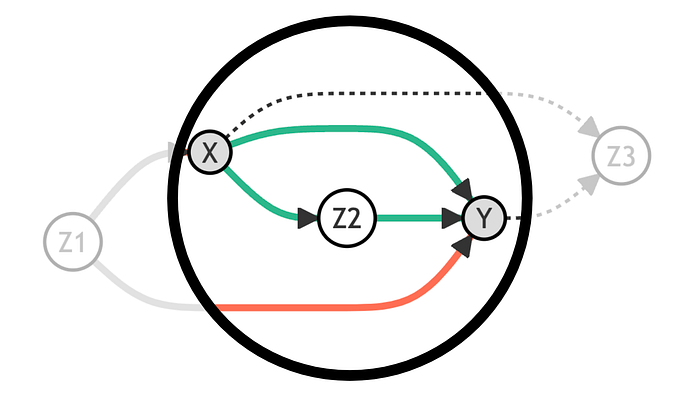
让我们绘制相同的图，用灰色表示我们正在以其为条件的变量，用虚线表示关闭的路径，用红线表示虚假的开放路径，用绿线表示因果的开放路径。

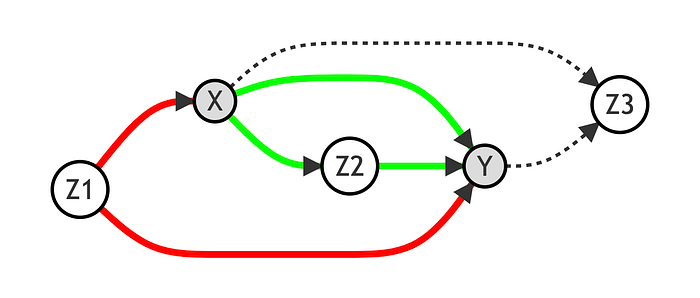
在这种情况下，为了评估 [X] 和 [Y] 之间的因果关系，我们需要关闭通过 [Z_1] 的路径。我们可以通过以 [Z_1] 为条件进行分析来做到这一点。

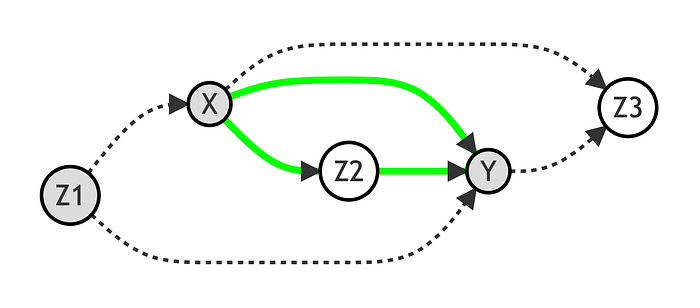
现在，通过以 [Z_1] 为条件，我们能够恢复 [X] 和 [Y] 之间的因果关系。

如果我们也以 [Z_2] 为条件会发生什么？在这种情况下，我们将关闭通过 [Z_2] 的路径，只留下 [X] 和 [Y] 之间的直接路径开放。然后，我们将只恢复 [X] 对 [Y] 的直接效应，而不是间接效应。

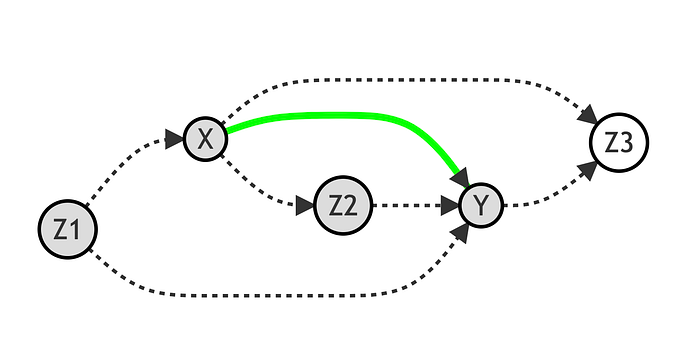
如果我们也以 [Z_3] 为条件会发生什么？在这种情况下，我们将打开通过 [Z_3] 的路径，这是一条虚假路径。这样，我们将无法恢复 [X] 对 [Y] 的因果效应。

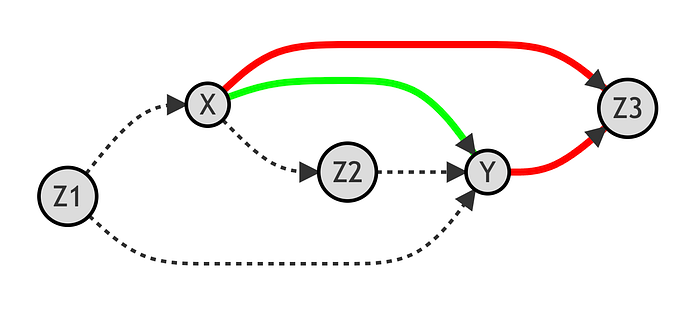
2 示例：班级规模与数学成绩

假设你对班级规模对数学成绩的影响感兴趣。更大的班级对学生的表现是更好还是更差？

假设数据生成过程可以用以下DAG表示。

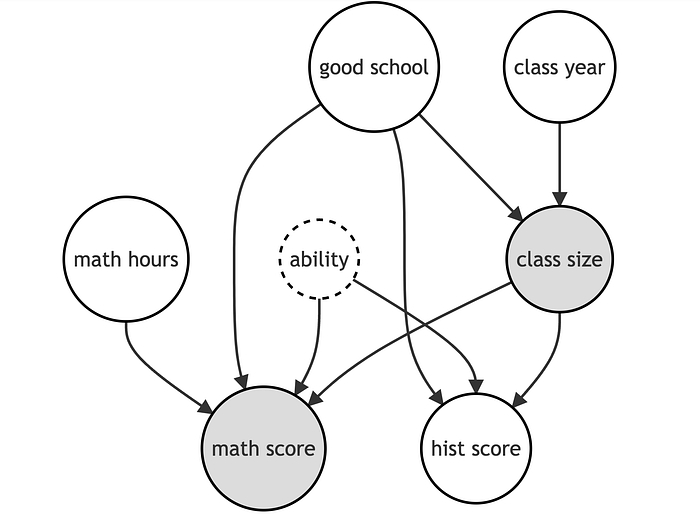
感兴趣的变量已被突出显示。此外，ability 周围的虚线表示这是一个我们在数据中未观察到的变量。

我们现在可以加载数据并查看其内容。数据是模拟的，你可以在这里找到原始数据生成过程。

from src.dgp import dgp_school
df = dgp_school().generate_data()
df.head()

png

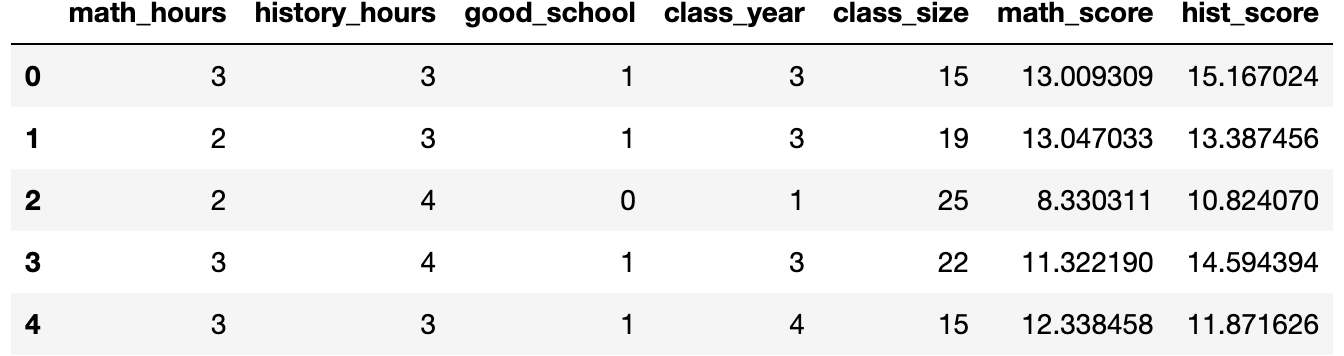
为了估计 class_size 对 math_scores 的因果效应，我们应该以哪些变量为条件进行回归？

首先，让我们看看如果我们不以任何变量为条件，只用 math_score 对 class_size 进行回归会发生什么。我们使用 statsmodels 包进行统计分析。

import statsmodels.formula.api as smf
smf.ols('math_score ~ class_size', df).fit().summary().tables[1]

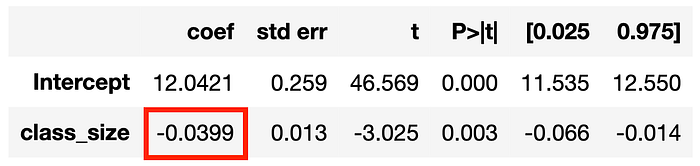
在表格的第二行，我们可以看到感兴趣的估计系数（class_size 的 coef）及其估计标准误差（std err）。class_size 的效应是负的，并且在统计上与零显著不同（p 值非常低，P>|t|=0.003）。

但是我们应该相信这个估计效应吗？在不控制任何变量的情况下，这是我们捕获的效应的 DAG 表示。

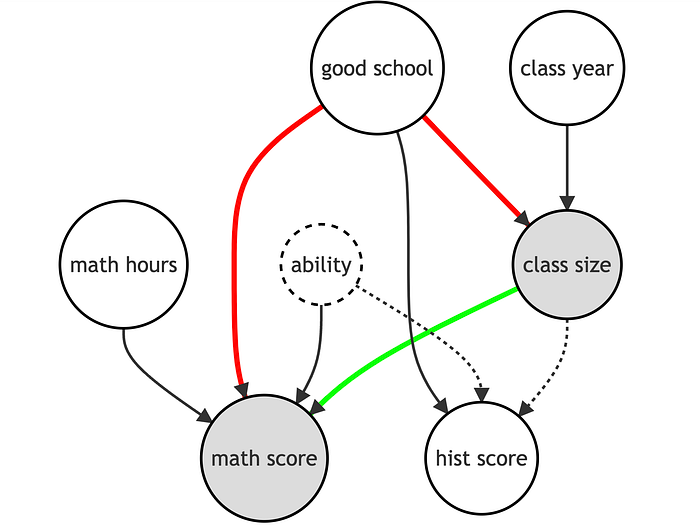
存在一条通过 good_school 的虚假路径，它偏差了我们估计的系数。直观地说，就读更好的学校会提高学生的数学成绩，而更好的学校可能班级规模更小。我们需要控制学校的质量。

smf.ols('math_score ~ class_size + good_school', df).fit().summary().tables[1]

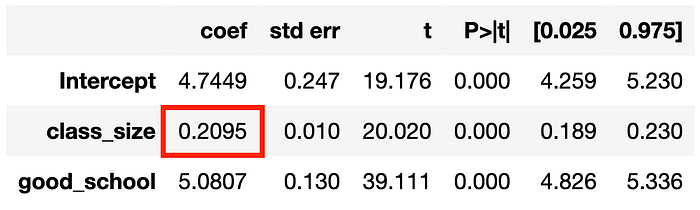
现在，class_size 对 math_score 效应的估计是无偏的！事实上，数据生成过程中的真实系数是 [0.2]。

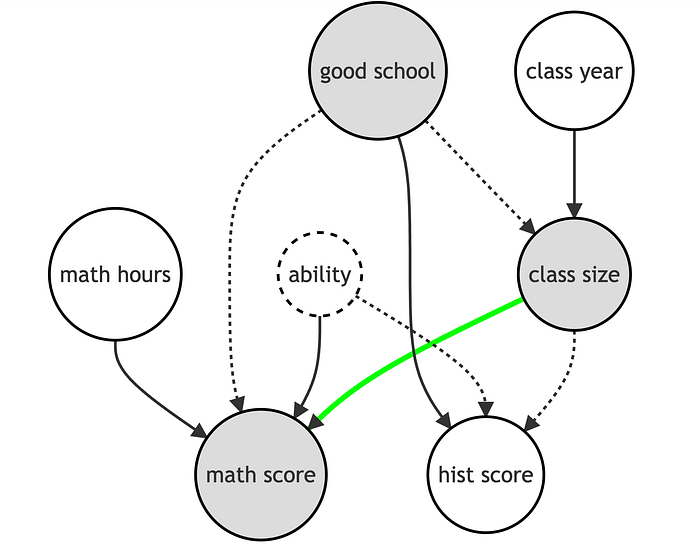
如果我们转而控制所有变量会发生什么？

smf.ols('math_score ~ class_size + good_school + math_hours + class_year + hist_score', df).fit().summary().tables[1]

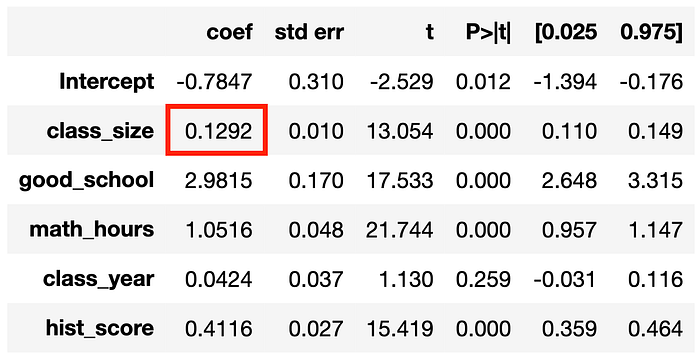
系数再次有偏。为什么？

通过控制 hist_score，我们打开了一条新的虚假路径。事实上，hist_score 是一个对撞点，控制它打开了一条通过 hist_score 和 ability 的路径，这条路径原本是关闭的。

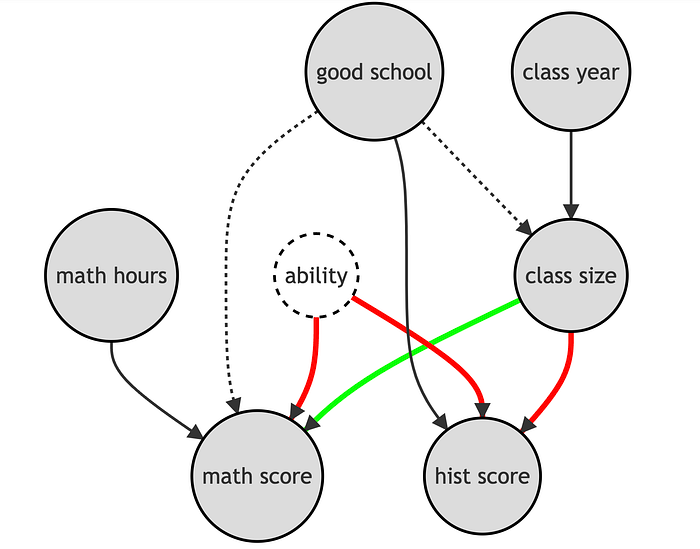
这个例子受到了以下推文的启发。

3 结论

在这篇文章中，我们探讨了如何使用有向无环图在因果分析中选择控制变量。DAGs 是非常有用的工具，因为它们提供了随机变量之间因果关系的直观图形表示。与“信息越多越好”的普遍直觉相反，有时包含额外的变量可能会使分析产生偏差，从而阻碍对结果的因果解释。特别是，我们必须注意不要包含对撞点，因为它们会打开原本会关闭的虚假路径。