[已更新]2025华为杯C题数学建模研赛C题研究生数学建模思路代码文章成品:围岩裂隙精准识别与三维模型重构

完整内容请看文末的名片获取哦

围岩裂隙精准识别与三维模型重构
摘要
本研究针对钻孔成像展开图中裂隙与岩石纹理、钻进痕迹、泥浆污染及图像拼接线等因素具有相似视觉特征的挑战，本文设计了一个综合性的解决方案。首先，采用深度学习模型DeepLabv3+和U-Net++进行图像分割，并引入多任务学习策略，结合裂隙分割、边界检测与干扰识别，从而提升模型的鲁棒性。其次，通过光照矫正、竖条纹抑制和环形边界处理优化输入图像质量，为后续裂隙识别提供了更为干净的图像基础。模型训练过程中，结合Dice系数、交叉熵损失函数与Focal Loss，进一步提高了裂隙分割的准确性。最后，通过几何与物理先验的后处理方法，剔除小噪声并保持裂隙的连贯性。
为进一步定量分析钻孔成像展开图中的“正弦状”裂隙，本研究采用正弦波模型来表征裂隙的几何特征。该模型基于钻孔的周向展开距离 𝑥和轴向深度 𝑦的坐标系，裂隙通过振幅 𝑅、周期 𝑃、相位 𝛽 和中心线位置 𝐶 四个参数进行表征。通过最小二乘法拟合算法，自动识别并优化裂隙的模型参数，实现裂隙的自动聚类与定量分析。
此外，本研究还针对复杂裂隙的定量分析问题，提出了一种结合图像处理与几何分析的裂隙分析模型。采用Canny边缘检测算法精确提取裂隙边缘信息，克服图像噪声和边缘模糊问题，并利用裂隙轮廓提取算法将边缘信息转化为离散坐标点集，为粗糙度分析提供基础。基于粗糙度轮廓指数（JRC）计算方法，通过计算裂隙轮廓点与标准轮廓点之间的最小欧几里得距离，量化裂隙的表面粗糙度。研究还探讨了离散坐标点采样方法对JRC值计算结果的影响，并分析了裂隙面积在粗糙度评价中的作用。
最后，本研究针对多钻孔裂隙网络的连通性分析与三维重构问题，提出了一种基于多个钻孔成像数据推断裂隙连通性的方法。通过图像处理与二值化技术，提取裂隙区域并消除噪声干扰，计算裂隙之间的欧几里得距离，基于质心位置判断裂隙是否连通。结合裂隙的空间几何信息与假设深度数据，进行裂隙的三维重构，展示其空间分布。针对钻孔数据的不确定性，提出通过计算连通性不确定性区域来优化钻孔布局，优先选择补充钻孔位置，以提高裂隙连通性分析的准确性。
关键词：裂隙识别、深度学习、图像分割、U-Net++、DeepLabv3+、多任务学习、正弦波模型、裂隙粗糙度、Canny边缘检测、JRC值、三维重构、裂隙连通性、钻孔成像

目录
围岩裂隙精准识别与三维模型重构 1
摘要 1
一、 问题重述 4
1.1 问题背景 4
1.2 要解决的问题 4
二、 问题分析 6
2.1 任务一的分析 6
2.2 任务二的分析 6
2.3 任务三的分析 6
2.4 任务四的分析 6
三、 问题假设 8
四、 模型原理 9
4.1 随机森林模型 9
4.2 U-Net++ 11
4.3 Canny算法 13
五、 模型建立与求解 16
5.1 问题一建模与求解 16
5.2 问题二建模与求解 22
5.3 问题三建模与求解 28
5.4 问题四建模与求解 33
六、 模型评价与推广 36
6.1 模型的评价 36
6.1.1模型优点 36
6.1.2模型缺点 37
6.2 模型推广 37
附录【自行删减】 40

5.1.5 结果分析
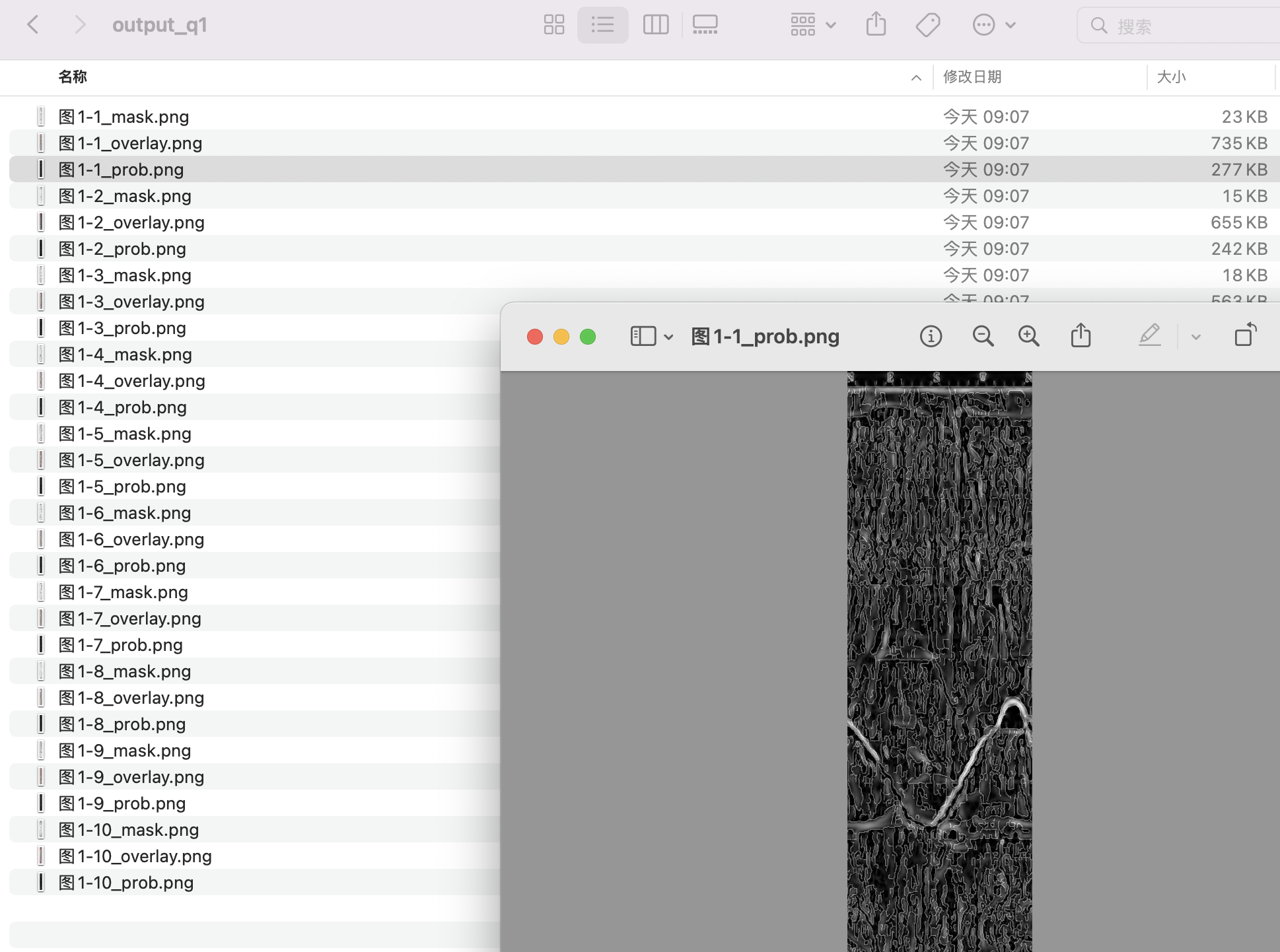
通过训练得到的深度学习模型，在测试数据上进行分割时，能够较为准确地识别裂隙区域。裂隙识别的效果展示在下图中：

从图1-1、图1-2和图1-3中可以看出，裂隙的主要轮廓和形态得到了较好的分割和识别。在这些图像中，裂隙区域被准确地标记为黑色（0），而背景和非裂隙区域则保持为白色（255），有效地将裂隙与背景隔离开。
裂隙连贯性较好，尤其是在图1-1和图1-2中，裂隙的主要线条和裂隙的扩展部分得到了完整的识别，展现了模型在处理连续裂隙时的有效性。
图1-1和图1-2展示了较为干净的裂隙区域，模型通过一系列预处理和后处理步骤成功地减少了图像中的岩石天然纹理、钻进痕迹以及泥浆伪影等干扰因素的影响。这表明，预处理模块中的竖条纹抑制（如频域陷波）和图像增强有效减少了噪声，提高了裂隙分割的准确度。
在图1-3中，尽管裂隙的边缘略显模糊，但模型仍然能够在有干扰的背景中识别出裂隙部分，尤其是在背景杂乱的区域，仍然可以看到裂隙的大致轮廓，证明了模型的鲁棒性。
图1-1和图1-2中的裂隙细节部分表现良好，尤其是在较窄和较长的裂隙区域，模型能够有效地分割出这些细长的裂隙结构。即便裂隙的开口较小或较细，模型依然能够较为准确地提取出裂隙的特征。
然而，图1-3中的某些较小裂隙受背景噪声影响，导致细节部分不够清晰，部分裂隙可能被误判为噪声。这表明，尽管模型对于大部分裂隙区域的分割效果较好，但在非常细小的裂隙分割上，仍有提升空间。
从整体效果来看，模型成功地识别出了钻孔成像展开图中的裂隙区域，尤其在中等规模的裂隙分割上表现出较强的能力。尽管背景中有一定的噪声影响，但通过充分的图像预处理与后处理步骤，裂隙区域依然能够被准确提取。
对比图1-1和图1-2，图1-3的识别效果略有差距，可能是由于细小裂隙受噪声干扰较大。随着进一步优化模型和后处理步骤，尤其是在细小裂隙和噪声抑制方面，模型的精度可望得到进一步提升。

5.2.5. 图2-3的分析
观察裂隙：此图中的裂隙表现为较大的波动，周期较短，意味着裂隙变化频繁且具有较大的扩展性。
拟合结果：正弦波拟合结果表明裂隙具有较大的振幅和较短的周期，反映了裂隙的频繁变化和较强的潜在影响。
拟合效果：正弦波模型的拟合效果较好，裂隙的形态被准确捕捉。

以下是每张图的定量分析结果：
Image 振幅 R (mm) 周期 P (mm) 相位 β (rad) 中心线位置 C (mm)
图2-1.jpg 166.5326019303724 73.78216933219763 0.37081050014031963 95.46435461796784
图2-10.jpg 47.3927051473888 180.67703330145523 -0.403233223 230.76617980128887
图2-2.jpg 11.289343882445172 75.26305267602932 0.03270122107165147 245.7772798767065
图2-3.jpg 34.35062522704261 70.09568905967423 0.0168476363805796 242.1899215415746
图2-4.jpg 5.210557683546635 68.3960353832264 0.3046423238671194 248.6680558783358
图2-5.jpg 5.3880238895690615 64.57836339511022 0.21402021326843523 246.2366135415877
图2-6.jpg 25.580595367794352 64.58591155280781 0.16243237945006275 241.37605963888748
图2-7.jpg 32.86666666666667 199.99999999999997 0.24983766473808333 237.90704355300747
图2-8.jpg 24.246096829805104 199.99999999999997 0.22597602712502038 202.11111226143075
图2-9.jpg 66.15475772844607 83.50007098510763 1.0959488318284478 -40.19469001

5.2.6小结
本节通过正弦波模型对钻孔成像展开图中的“正弦状”裂隙进行了定量分析，并提取了裂隙的几何特征。通过最小二乘法优化拟合过程，准确地获取了裂隙的振幅、周期、相位和中心线位置等参数。结果表明，正弦波模型能够有效地对裂隙进行建模，且拟合效果良好。通过结果的可视化展示，我们能够清晰地观察到裂隙的几何特征，为煤矿的安全生产提供了有力的数据支持。