【Leetcode hot 100】199.二叉树的右视图
问题链接
199.二叉树的右视图
问题描述
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
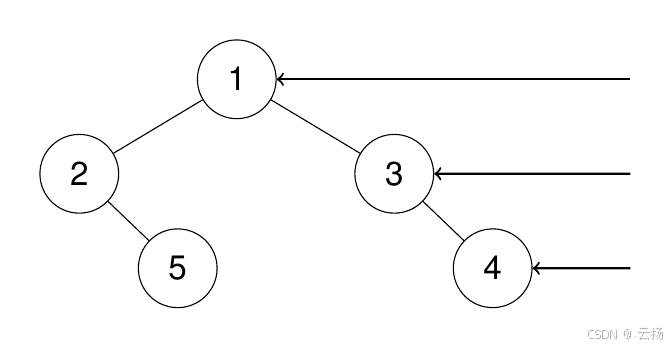
输入:root = [1,2,3,null,5,null,4]
输出:[1,3,4]
解释:
示例 2:
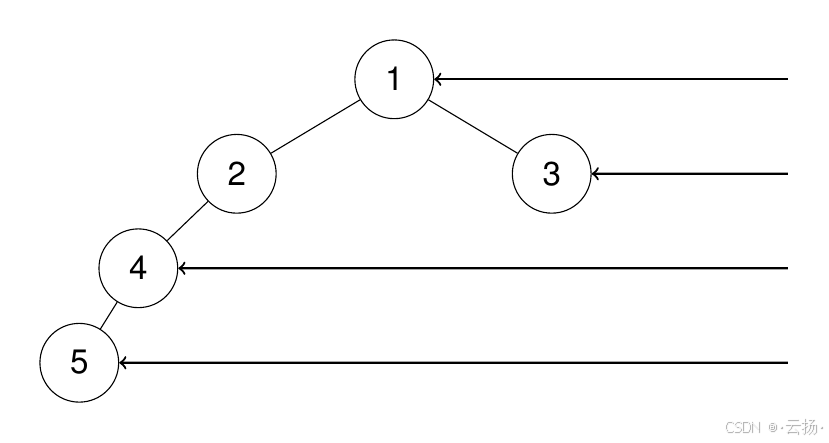
输入:root = [1,2,3,4,null,null,null,5]
输出:[1,3,4,5]
解释:
示例 3:
输入:root = [1,null,3]
输出:[1,3]
示例 4:
输入:root = []
输出:[]
提示:
- 二叉树的节点个数的范围是
[0,100] -100 <= Node.val <= 100
问题解答
方法一:广度优先搜索(BFS)
思路解析
BFS 是「层序遍历」的典型实现,通过队列存储每一层的节点,遍历每一层时:
- 记录当前层的节点总数(队列大小),确保只处理当前层的节点;
- 遍历当前层的所有节点,仅将最后一个节点的值加入结果列表(即当前层的最右侧节点);
- 同时将当前节点的左、右子节点(若存在)依次加入队列,为下一层遍历做准备。
代码实现
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;// 二叉树节点定义(题目已给出,此处为完整性包含)
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {public List<Integer> rightSideView(TreeNode root) {// 结果列表,存储右视图节点值List<Integer> result = new ArrayList<>();if (root == null) {return result; // 根节点为空,直接返回空列表}// 初始化队列,用于BFS层序遍历Queue<TreeNode> queue = new LinkedList<>();queue.offer(root); // 将根节点加入队列// 遍历每一层while (!queue.isEmpty()) {// 关键:获取当前层的节点总数(队列此时的大小)int levelSize = queue.size();// 遍历当前层的所有节点for (int i = 0; i < levelSize; i++) {TreeNode currentNode = queue.poll(); // 取出队首节点// 若为当前层最后一个节点,加入结果列表if (i == levelSize - 1) {result.add(currentNode.val);}// 将当前节点的左、右子节点加入队列(左先右后,不影响最后取右)if (currentNode.left != null) {queue.offer(currentNode.left);}if (currentNode.right != null) {queue.offer(currentNode.right);}}}return result;}
}
方法二:深度优先搜索(DFS)
思路解析
DFS 通过递归遍历二叉树,核心是先访问右子树,再访问左子树(确保每一层的最右侧节点优先被访问):
- 维护一个「当前最大深度」变量,记录已加入结果列表的节点所在的最大深度;
- 递归时,若当前节点的深度 > 「当前最大深度」,说明该节点是当前层的最右侧节点(因先访问右子树),将其加入结果列表,并更新「当前最大深度」;
- 按「右子树 → 左子树」的顺序递归,确保每一层的最右侧节点先被处理。
代码实现
import java.util.ArrayList;
import java.util.List;class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {// 结果列表private List<Integer> result = new ArrayList<>();// 当前最大深度(用数组存储,避免递归中值传递的问题)private int[] maxDepth = {0};public List<Integer> rightSideView(TreeNode root) {// 从根节点开始,初始深度为1(根节点是第1层)dfs(root, 1);return result;}// 递归方法:currentNode=当前节点,currentDepth=当前节点的深度private void dfs(TreeNode currentNode, int currentDepth) {if (currentNode == null) {return; // 递归终止条件:节点为空}// 若当前深度 > 最大深度,说明是当前层最右侧节点if (currentDepth > maxDepth[0]) {result.add(currentNode.val);maxDepth[0] = currentDepth; // 更新最大深度}// 先递归右子树(确保右节点优先被访问),再递归左子树dfs(currentNode.right, currentDepth + 1);dfs(currentNode.left, currentDepth + 1);}
}
两种方法对比
| 维度 | 广度优先搜索(BFS) | 深度优先搜索(DFS) |
|---|---|---|
| 核心逻辑 | 按层遍历,取每一层最后节点 | 先右后左遍历,取每层首个节点 |
| 时间复杂度 | O(n)(每个节点访问1次) | O(n)(每个节点访问1次) |
| 空间复杂度 | O(n)(队列存储最多一层节点,最坏为n) | O(n)(递归栈深度,最坏为n,如斜树) |
| 适用场景 | 更直观理解“层”的概念 | 代码更简洁,递归逻辑清晰 |