【LeetCode hot100|Week3】数组，矩阵

笔记用于个人复习和巩固，题解非原创，参考LeetCode官方题解以及各个大佬的解法，希望给大家带来帮助，同时笔记也能督促我学习进步

这周主要把数组和矩阵的题目刷了一遍

Week3

D1

189. 轮转数组

189. 轮转数组

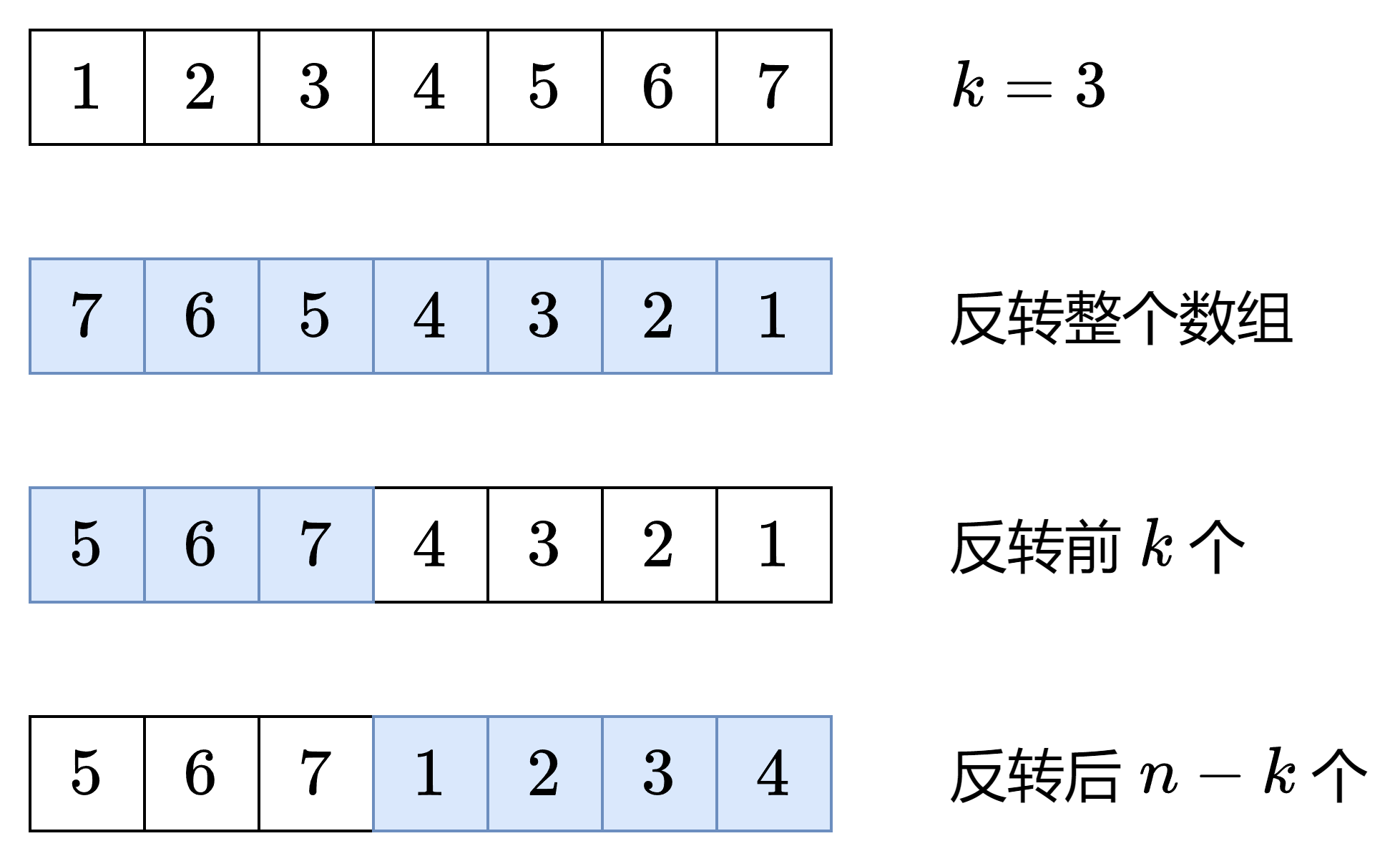
把A + B变成B + A：

• 先反转整个数组
• 再分别反转A和B

class Solution {public void rotate(int[] nums, int k) {int n = nums.length;k %= n; // 轮转 k 次等于轮转 k % n 次reverse(nums, 0, n - 1);reverse(nums, 0, k - 1);reverse(nums, k, n - 1);}private void reverse(int[] nums, int i, int j) {while (i < j) {int temp = nums[i];nums[i++] = nums[j];nums[j--] = temp;}}
}

D2

238. 除自身以外数组的乘积

238. 除自身以外数组的乘积

前缀积和后缀积

class Solution {public int[] productExceptSelf(int[] nums) {int n = nums.length;int[] answer = new int[n];int[] pre = new int[n];int[] suf = new int[n];pre[0] = nums[0];suf[0] = nums[n - 1];for(int i = 1;i < n;i++){pre[i] = pre[i - 1] * nums[i];suf[i] = suf[i - 1] * nums[n - 1 -i];}answer[0] = suf[n - 2];answer[n - 1] = pre[n - 2];for(int i = 1;i < n - 1;i++){answer[i] = pre[i - 1]*suf[n - 1 - 1 - i];}return answer;}
}

照灵茶山的优化一下索引

灵茶山版本的 suf[i] 直接表示“从 i+1 到 n-1 的积”，索引清晰，无需转换

//灵茶山版
class Solution {public int[] productExceptSelf(int[] nums) {int n = nums.length;int[] pre = new int[n];pre[0] = 1; //初始化为1for (int i = 1; i < n; i++) {pre[i] = pre[i - 1] * nums[i - 1];}int[] suf = new int[n];suf[n - 1] = 1;for (int i = n - 2; i >= 0; i--) {suf[i] = suf[i + 1] * nums[i + 1];}int[] ans = new int[n];for (int i = 0; i < n; i++) {ans[i] = pre[i] * suf[i];}return ans;}
}

//个人改进版
class Solution {public int[] productExceptSelf(int[] nums) {int n = nums.length;int[] answer = new int[n];int[] pre = new int[n];int[] suf = new int[n];pre[0] = nums[0];suf[n - 1] = nums[n - 1];for(int i = 1;i < n;i++){pre[i] = pre[i - 1] * nums[i];}for(int i = n - 2;i >= 0;i--){suf[i] = suf[i + 1] * nums[i];}answer[0] = suf[1];answer[n - 1] = pre[n - 2];for(int i = 1;i < n - 1;i++){answer[i] = pre[i - 1]*suf[i + 1];}return answer;}
}

D3

41. 缺失的第一个正数

41. 缺失的第一个正数

原地哈希：将原来的数组视为哈希表

• 要找的数一定是在[1,N+1]里的整数
• 把1放在下标为0的位置上，把2放在下标为1的位置上…

class Solution {public int firstMissingPositive(int[] nums) {int n = nums.length;for (int i = 0; i < n; i++) {// 如果当前学生的学号在 [1,n] 中，但（真身）没有坐在正确的座位上while (1 <= nums[i] && nums[i] <= n && nums[i] != nums[nums[i] - 1]) {// 那么就交换 nums[i] 和 nums[j]，其中 j 是 i 的学号int j = nums[i] - 1; // 减一是因为数组下标从 0 开始int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}}// 找第一个学号与座位编号不匹配的学生for (int i = 0; i < n; i++) {if (nums[i] != i + 1) {return i + 1;}}// 所有学生都坐在正确的座位上return n + 1;}
}//作者：灵茶山艾府

如果空间复杂度没要求 就用哈希表

class Solution {public int firstMissingPositive(int[] nums) {int n = nums.length;Set<Integer>hashSet = new HashSet<>();for(int num : nums){hashSet.add(num);}for(int i = 1;i < n;i++){if(!hashSet.contains(i)){return i;}}return n + 1;}
}

D4

73. 矩阵置零

73. 矩阵置零

用两个标记数组分别记录每一行和每一列是否有零出现。

• 首先遍历该数组一次，如果某个元素为 0，那么就将该元素所在的行和列所对应标记数组的位置置为 true
• 最后再次遍历该数组，用标记数组更新原数组

class Solution {public void setZeroes(int[][] matrix) {int m = matrix.length, n = matrix[0].length;boolean[] row = new boolean[m];boolean[] col = new boolean[n];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (matrix[i][j] == 0) {row[i] = col[j] = true;}}}for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (row[i] || col[j]) {matrix[i][j] = 0;}}}}
}

D5

54. 螺旋矩阵

54. 螺旋矩阵

示例 2 这 12 个数字，可以分为以下 5 组：

• 1→2→3→4
• 8→12
• 11→10→9
• 5
• 6→7

其中第 1,3,5 组都是向右或者向左走的，长度依次为 4,3,2，这是一个从 n=4 开始的逐渐递减的序列。

其中第 2,4 组都是向下或者向上走的，长度依次为 2,1，这是一个从 m−1=2 开始的逐渐递减的序列。

由于走的步数是有规律的，我们可以精确地控制在每个方向上要走多少步，无需判断是否出界、是否重复访问：

• 从 (0,−1) 开始。

• 一开始，向右走 n 步，每次先走一步，再把数字加入答案。走 n 步即 1→2→3→4，矩阵第一排的数都加入了答案。

• 然后向下走 m−1 步，即 8→12。

• 然后向左走 n−1 步，即 11→10→9。

• 然后向上走 m−2 步，即 5。

• 然后向右走 n−2 步，即 6→7。

• 重复上述过程，直到答案的长度等于 mn。

代码实现时，可以这样简化代码：

• 一开始走 n 步。

• 把 n,m 分别更新为 m−1,n，这样下一轮循环又可以走 n 步（相当于走了 m−1 步），无需修改其他逻辑。

• 把 n,m 分别更新为 m−1,n，这样下一轮循环又可以走 n 步（相当于走了 n−1 步）。

• 把 n,m 分别更新为 m−1,n，这样下一轮循环又可以走 n 步（相当于走了 m−2 步）。

• 依此类推，每次只需把 n,m 分别更新为 m−1,n 即可。

class Solution {private static final int[][] DIRS = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // 右下左上public List<Integer> spiralOrder(int[][] matrix) {int m = matrix.length;int n = matrix[0].length;int size = m * n;List<Integer> ans = new ArrayList<>(m * n); // 预分配空间int i = 0;int j = -1; // 从 (0, -1) 开始for (int di = 0; ans.size() < size; di = (di + 1) % 4) {for (int k = 0; k < n; k++) { // 走 n 步（注意 n 会减少）i += DIRS[di][0];j += DIRS[di][1]; // 先走一步ans.add(matrix[i][j]); // 再加入答案}int tmp = n;n = m - 1; // 减少后面的循环次数（步数）m = tmp;}return ans;}
}

D6

48. 旋转图像

48. 旋转图像

class Solution {public void rotate(int[][] matrix) {int n = matrix.length;int[][] matrix_new = new int[n][n];for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {matrix_new[j][n - i - 1] = matrix[i][j];}}for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {matrix[i][j] = matrix_new[i][j];}}}
}

matrix_new[col][n−row−1]=matrix[row][col]

matrix[n−row−1][n−col−1]=matrix[col][n−row−1]

D7

240. 搜索二维矩阵 II

240. 搜索二维矩阵 II

排除法

class Solution {public boolean searchMatrix(int[][] matrix, int target) {int i = 0;int j = matrix[0].length - 1;while(i < matrix.length && j >= 0){if(matrix[i][j] == target){return true;}else if(matrix[i][j] < target){i++;}else{j--;}}return false;}
}