【论文阅读】-《Triangle Attack: A Query-efficient Decision-based Adversarial Attack》
三角攻击:一种查询高效的基于决策的对抗攻击

原文链接:https://arxiv.org/abs/2112.06569
摘要
基于决策的攻击对现实世界应用构成了严重威胁,因为它将目标模型视为黑盒,并且只能访问硬预测标签。最近已经付出了巨大努力来减少查询次数;然而,现有的基于决策的攻击仍然需要数千次查询才能生成高质量的对抗样本。在这项工作中,我们发现对于任何迭代攻击,一个良性样本、当前和下一个对抗样本可以在子空间中自然地构建一个三角形。基于正弦定理,我们提出了一种新颖的三角攻击(TA),利用几何信息(即在任何三角形中,较长的边总是对着较大的角)来优化扰动。然而,直接在输入图像上应用此类信息是无效的,因为它无法在高维空间中彻底探索输入样本的邻域。为了解决这个问题,TA 在低频空间中优化扰动以实现有效的降维,这得益于这种几何特性的普遍性。在 ImageNet 数据集上的广泛评估表明,TA 在 1000 次查询内实现了更高的攻击成功率,并且在各种扰动预算下,达到相同攻击成功率所需的查询次数远少于现有的基于决策的攻击。凭借如此高的效率,我们进一步验证了 TA 在现实世界 API(即腾讯云 API)上的适用性。
1 引言
尽管深度神经网络(DNNs)取得了前所未有的进展 [27, 24, 25],但对对抗样本 [47] 的脆弱性给安全敏感的应用带来了严重威胁,例如人脸识别 [42, 48, 20, 30, 56, 50, 15, 37, 62]、自动驾驶 [7, 19, 4, 61, 40] 等。为了在各种现实世界应用中安全部署 DNNs,有必要对对抗样本的内在特性进行深入分析,这激发了对对抗攻击 [36, 6, 3, 11, 8, 17, 5, 52] 和防御 [34, 23, 64, 57, 58, 53] 的大量研究。现有的攻击可以分为两类:白盒攻击完全了解目标模型(通常利用梯度)[21, 6, 34, 17],而黑盒攻击只能访问模型输出,这在现实世界场景中更具适用性。
黑盒攻击可以通过不同的方式实现。基于迁移的攻击 [32, 17, 60, 55] 采用在替代模型上生成的对抗样本来直接欺骗目标模型。基于分数的攻击 [9, 26, 2, 31] 假设攻击者可以访问输出 logits,而基于决策(又名硬标签)的攻击 [5, 11, 10, 29, 35] 只能访问预测(top-1)标签。
在黑盒攻击中,由于攻击所需的信息要求最少,基于决策的攻击更具挑战性和实用性。对目标模型的查询次数通常在基于决策的攻击中起着重要作用,因为在实践中,对受害模型的访问通常是受限的。尽管最近的工作设法将总查询次数从数百万次减少到数千次 [5, 29, 38],但对于大多数实际应用来说仍然不足 [35]。
现有的基于决策的攻击 [5, 29, 38, 35] 首先在对抗空间中生成一个大的对抗扰动,然后通过各种优化方法在保持对抗性的同时最小化扰动。如图 1 所示,我们发现在第 ttt 次迭代时,对于任何迭代攻击,良性样本 xxx、当前对抗样本 xtadvx_{t}^{adv}xtadv 和下一个对抗样本 xt+1advx_{t+1}^{adv}xt+1adv 可以自然地构建一个三角形。根据正弦定理,第 (t+1)(t+1)(t+1) 次迭代的对抗样本 xt+1advx_{t+1}^{adv}xt+1adv 应满足 βt+2αt>π\beta_{t}+2\alpha_{t}>\piβt+2αt>π 以保证扰动减小,即 δt+1=∥xt+1adv−x∥p<δt=∥xtadv−x∥p\delta_{t+1}=\|x_{t+1}^{adv}-x\|_{p}<\delta_{t}=\|x_{t}^{adv}-x\|_{p}δt+1=∥xt+1adv−x∥p<δt=∥xtadv−x∥p(当 βt+2⋅αt=π\beta_{t}+2\cdot\alpha_{t}=\piβt+2⋅αt=π 时,将是一个等腰三角形,即 δt+1=δt\delta_{t+1}=\delta_{t}δt+1=δt)。
基于上述几何特性,我们提出了一种新颖且查询高效的基于决策的攻击,称为三角攻击(TA)。具体来说,在第 ttt 次迭代时,我们随机选择一条穿过良性样本 xxx 的方向线来确定一个 2 维子空间,在该子空间中,我们基于当前对抗样本 xtadvx_{t}^{adv}xtadv、良性样本 xxx、学习到的角度 αt\alpha_{t}αt 和搜索到的角度 βt\beta_{t}βt 迭代地构建三角形,直到构建的三角形的第三个顶点具有对抗性。利用几何信息,我们可以在由离散余弦变换(DCT)[1] 生成的低频空间中进行 TA,以实现有效的降维,从而提高效率。并且我们进一步更新 αt\alpha_{t}αt 以适应每个构建三角形的扰动优化。与大多数现有的基于决策的攻击不同,TA 不需要将 xtadvx_{t}^{adv}xtadv 限制在决策边界上或在每次迭代时估计梯度,这使得 TA 具有查询高效性。
我们的主要贡献总结如下:
- 据我们所知,这是第一个通过几何信息直接在频率空间中优化扰动,而不将对抗样本限制在决策边界上的工作,从而实现了高查询效率。
- 在 ImageNet 数据集上的广泛评估表明,TA 在 1000 次查询内表现出更高的攻击成功率,并且在五个模型上,达到相同扰动预算下的相同攻击成功率所需的查询次数远少于现有的 SOTA 攻击 [11, 12, 8, 29, 38, 35]。
- TA 在腾讯云 API 上生成了更多具有不可感知扰动的对抗样本,显示了其工业级的适用性。
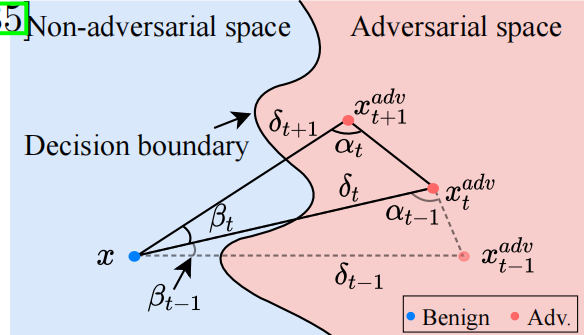
图 1: TA 在任意迭代时的候选三角形示意图。在第 ttt 次迭代时,TA 在采样的子空间中构建一个具有学习角度 αt\alpha_{t}αt 的三角形,该角度满足 βt+2αt>π\beta_{t}+2\alpha_{t}>\piβt+2αt>π,以找到新的对抗样本 xt+1advx_{t+1}^{adv}xt+1adv 并相应地更新 αt\alpha_{t}αt。请注意,与现有的基于决策的攻击 [5, 38, 35] 不同,TA 不将 xtadvx_{t}^{adv}xtadv 限制在决策边界上,而是利用几何特性在低频空间中最小化扰动;这使得 TA 本身具有查询高效性。
2 相关工作
自从 Szegedy 等人 [47] 发现对抗样本以来,已经提出了大量的对抗攻击来欺骗 DNNs。白盒攻击,例如基于单步梯度的攻击 [21]、基于迭代梯度的攻击 [36, 28, 34, 14] 和基于优化的攻击 [47, 6, 3],通常利用梯度并表现出良好的攻击性能。它们已被广泛用于评估防御措施的模型鲁棒性 [34, 64, 41, 13, 16],但在信息有限的现实世界中难以应用。为了使对抗攻击在实践中适用,各种黑盒攻击,包括基于迁移的攻击 [17, 60, 51, 52, 59]、基于分数的攻击 [9, 26, 49, 2, 18, 63, 65] 和基于决策的攻击 [5, 12, 8, 38, 35],引起了越来越多的兴趣。其中,基于决策的攻击最具挑战性,因为它只能访问预测标签。在这项工作中,我们旨在通过利用几何信息来提高基于决策攻击的查询效率,并简要概述现有的基于决策的攻击。
BoundaryAttack [5] 是第一个基于决策的攻击,它初始化一个大的扰动,并在保持对抗性的同时在决策边界上执行随机游走。这种范式已被后续的基于决策的攻击广泛采用。OPT [11] 将基于决策的攻击表述为一个带有零阶优化的实值优化问题。SignOPT [12] 进一步计算方向导数的符号而不是幅度以实现快速收敛。HopSkipJumpAttack (HSJA) [8] 通过在决策边界上利用二进制信息估计梯度方向来改进 BoundaryAttack。QEBA [29] 使用从各种子空间(包括空间、频率和内在分量)采样的扰动来增强 HSJA,以实现更好的梯度估计。为了进一步提高查询效率,qPool [33] 假设边界在对抗样本附近的曲率很小,并采用多个扰动向量进行有效的梯度估计。BO [43] 使用贝叶斯优化在低维子空间中寻找对抗扰动,并将其映射回原始输入空间以获得最终扰动。GeoDA [38] 通过超平面近似局部决策边界,并搜索超平面上最接近良性样本的点作为对抗样本。Surface [35] 迭代地在决策边界上构建一个圆,并采用二分搜索来找到构建的圆与决策边界的交点作为对抗样本,无需任何梯度估计。
大多数现有的基于决策的攻击将每次迭代的对抗样本限制在决策边界上,并且通常采用不同的梯度估计方法进行攻击。在这项工作中,我们提出三角攻击来最小化
通过利用正弦定理,直接在低频空间中最小化对抗扰动,而无需梯度估计或将对抗样本限制在决策边界上,从而实现高效的基于决策的攻击。
3 方法
在本节中,我们首先提供预备知识。然后我们介绍我们的动机和提出的三角攻击(TA)。
3.1 预备知识
给定一个带有参数 θ\thetaθ 的分类器 fff 和一个带有真实标签 y∈Yy\in\mathcal{Y}y∈Y 的良性样本 x∈Xx\in\mathcal{X}x∈X,其中 X\mathcal{X}X 表示所有图像,Y\mathcal{Y}Y 是输出空间。对抗攻击寻找一个对抗样本 xadv∈Xx^{adv}\in\mathcal{X}xadv∈X 来误导目标模型:
f(xadv;θ)≠f(x;θ)=ys.t.∥xadv−x∥p<ϵ,f(x^{adv};\theta)\neq f(x;\theta)=y\quad\text{s.t.}\quad\|x^{adv}-x\|_{p}<\epsilon,f(xadv;θ)=f(x;θ)=ys.t.∥xadv−x∥p<ϵ,
其中 ϵ\epsilonϵ 是扰动预算。基于决策的攻击通常首先生成一个大的对抗扰动 δ\deltaδ,然后最小化扰动如下:
min∥δ∥ps.t.f(x+δ;θ)≠f(x;θ)=y.\min\|\delta\|_{p}\quad\text{s.t.}\quad f(x+\delta;\theta)\neq f(x;\theta)=y.min∥δ∥ps.t.f(x+δ;θ)=f(x;θ)=y. (1)
现有的基于决策的攻击 [11, 12, 29] 通常估计梯度以最小化扰动,这非常耗时。最近,一些工作采用几何特性来估计梯度或直接优化扰动。这里我们详细介绍了两种受几何启发的基于决策的攻击。
GeoDA[38] 认为,数据点 xxx 附近的决策边界可以通过一个穿过靠近 xxx 的边界点 xBx_{B}xB 且具有法向量 www 的超平面来局部近似。因此,方程(1)可以局部线性化:
min∥δ∥ps.t.w⊤(x+δ)−w⊤xB=0.\min\|\delta\|_{p}\quad\text{s.t.}\quad w^{\top}(x+\delta)-w^{\top}x_{B}=0.min∥δ∥ps.t.w⊤(x+δ)−w⊤xB=0.
这里 xBx_{B}xB 是边界上的一个数据点,可以通过二分搜索和一些查询找到,GeoDA 随机采样几个数据点来估计 www,以在每次迭代中优化扰动。
Surface[35] 假设边界可以在边界点 x+δx+\deltax+δ 附近通过超平面局部近似。在每次迭代中,它使用极坐标表示对抗样本,并搜索最优的 θ\thetaθ 来更新扰动:
δt+1=δtcosθ(ucosθ+vsinθ),\delta_{t+1}=\delta_{t}\cos\theta(\bm{u}\cos\theta+\bm{v}\sin\theta),δt+1=δtcosθ(ucosθ+vsinθ),
其中 u\bm{u}u 是从 xxx 到 xtadvx_{t}^{adv}xtadv 的单位向量,v\bm{v}v 是 u\bm{u}u 的正交向量。
3.2 动机
与大多数基于梯度估计 [11, 12, 29, 38] 或在决策边界上随机游走 [5, 35] 的基于决策的攻击不同,我们的目标是利用几何特性优化扰动,而无需任何用于梯度估计的查询。在生成一个大的对抗扰动之后,基于决策的
攻击在每次迭代中保持对抗性的同时,将对抗样本移近良性样本,即减小对抗扰动 δt\delta_{t}δt。在这项工作中,如图 1 所示,我们发现在第 ttt 次迭代时,对于任何迭代攻击,良性样本 xxx、当前对抗样本 xtadvx^{adv}_{t}xtadv 和下一个对抗样本 xt+1advx^{adv}_{t+1}xt+1adv 可以在子空间中自然地构建一个三角形。因此,搜索具有更小扰动的下一个对抗样本 xt+1advx^{adv}_{t+1}xt+1adv 等价于基于 xxx 和 xtadvx^{adv}_{t}xtadv 搜索一个三角形,其中第三个数据点 x′x^{\prime}x′ 具有对抗性并满足 ∥x′−x∥p<∥xtadv−x∥p\|x^{\prime}-x\|_{p}<\|x^{adv}_{t}-x\|_{p}∥x′−x∥p<∥xtadv−x∥p。这启发我们利用三角形中角度和边长的关系来搜索合适的三角形,以在每次迭代中最小化扰动。然而,如第 4.4 节所示,直接将这种几何特性应用于输入图像会导致性能非常差。得益于这种几何特性的普遍性,我们在由 DCT [1] 生成的低频空间中优化扰动以实现有效的降维,这表现出很高的攻击效率,如第 4.4 节所示。
此外,自从 Brendel 等人 [5] 提出 BoundaryAttack 以来,大多数基于决策的攻击 [11, 12, 8, 38, 35] 都遵循每次迭代的对抗样本应该在决策边界上的设置。我们认为这种限制在基于决策的攻击中不是必需的,但会引入太多对目标模型的查询来接近边界。因此,我们在这项工作中不采用这种约束,并在第 4.4 节中验证了这一论点。
3.3 三角攻击
在这项工作中,我们有以下假设:对于任何深度神经分类器 fff,都存在对抗样本:
假设 1。给定一个良性样本 xxx 和一个扰动预算 ϵ\epsilonϵ,存在一个朝向决策边界的对抗扰动 ∥δ∥p≤ϵ\|\delta\|_{p}\leq\epsilon∥δ∥p≤ϵ,可以误导目标分类器 fff。
这是一个普遍的假设,即我们可以为输入样本 xxx 找到对抗样本 xadvx^{adv}xadv,这已被大量工作 [21, 6, 3, 5, 54] 验证。如果这个假设不成立,目标模型是理想鲁棒的,以至于我们在扰动预算内找不到任何对抗样本,这超出了我们的讨论范围。因此,我们遵循现有基于决策攻击的框架,首先生成一个随机的大的对抗扰动,然后最小化扰动。为了与以前的工作保持一致,我们使用二分搜索 [29, 38, 35] 生成一个接近决策边界的随机扰动,并主要关注扰动优化。
在任何对抗攻击的扰动优化过程的任意两个连续迭代中,即不失一般性的第 ttt 次和第 (t+1)(t+1)(t+1) 次迭代,输入样本 xxx、当前对抗样本 xtadvx^{adv}_{t}xtadv 和下一个对抗样本 xt+1advx^{adv}_{t+1}xt+1adv 可以在输入空间 X\mathcal{X}X 的一个子空间中自然地构建一个三角形。因此,如图 1 所示,减小扰动以生成 xt+1advx^{adv}_{t+1}xt+1adv 等价于搜索一个合适的三角形,其三个顶点分别是 xxx、xtadvx^{adv}_{t}xtadv 和 xt+1advx^{adv}_{t+1}xt+1adv。
定理 1:(正弦定理)。假设 aaa、bbb 和 ccc 是三角形的边长,α\alphaα、β\betaβ 和 γ\gammaγ 是对角,我们有 asinα=bsinβ=csinγ\frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma}sinαa=sinβb=sinγc。
从定理 1,我们可以得到图 1 中三角形的边长与对角的关系:
δtsinαt=δt+1sin(π−(αt+βt)).\frac{\delta_{t}}{\sin\alpha_{t}}=\frac{\delta_{t+1}}{\sin\left(\pi-\left(\alpha_{t}+\beta_{t}\right)\right)}.sinαtδt=sin(π−(αt+βt))δt+1. (2)
为了贪婪地减小扰动 δt\delta_{t}δt,第 ttt 个三角形应满足 δt+1δt=\frac{\delta_{t+1}}{\delta_{t}}=δtδt+1=sin(π−(αt+βt))sinαt<1\frac{\sin\left(\pi-\left(\alpha_{t}+\beta_{t}\right)\right)}{\sin\alpha_{t}}<1sinαtsin(π−(αt+βt))<1,即 π−(αt+βt)<αt\pi-\left(\alpha_{t}+\beta_{t}\right)<\alpha_{t}π−(αt+βt)<αt。因此,在第 ttt 次迭代时减小扰动可以通过找到一个由输入样本 xxx、当前对抗样本 xtadvx_{t}^{adv}xtadv 以及角度 βt\beta_{t}βt 和 αt\alpha_{t}αt 构建的三角形来实现,该三角形满足 βt+2αt>π\beta_{t}+2\alpha_{t}>\piβt+2αt>π 并且第三个顶点应具有对抗性。我们将这样的三角形称为候选三角形,并将 T(x,xtadv,αt,βt,St)\mathcal{T}(x,x_{t}^{adv},\alpha_{t},\beta_{t},\mathcal{S}_{t})T(x,xtadv,αt,βt,St) 表示为第三个顶点,其中 St\mathcal{S}_{t}St 是采样的子空间。基于这一观察,我们提出了一种新颖的基于决策的攻击,称为三角攻击(TA),它在每次迭代时搜索候选三角形并相应地调整角度 αt\alpha_{t}αt。
在频率空间中采样 2 维子空间 S\mathcal{S}S。 输入图像通常位于高维空间中,例如 ImageNet [27] 的 224×224×3224\times 224\times 3224×224×3,这对于攻击来说太大,无法有效探索输入样本的邻域以最小化对抗扰动。以前的工作 [22, 29, 35] 已经表明,利用各种子空间中的信息可以提高基于决策攻击的效率。例如,QEBA [29] 在空间变换空间或低频空间中采样随机噪声进行梯度估计,但使用估计的梯度在输入空间中最小化扰动。Surface [35] 在由低频空间中随机采样的单位向量确定的输入空间的子空间中优化扰动。通常,低频空间包含图像最关键的信息。鉴于 TA 在输入空间中性能较差(如第 4.4 节所示)以及几何特性的普遍性(如图 2 所示),我们在每次迭代时直接在频率空间中优化扰动以实现有效的降维。并且我们在低频空间(前 10%)中随机采样一条穿过良性样本的 ddd 维线。采样的线、从良性样本 xxx 到当前对抗样本 xtadvx_{t}^{adv}xtadv 的方向线可以确定频率空间中一个唯一的 2 维子空间 S\mathcal{S}S,我们可以在其中构建候选三角形以最小化扰动。最终的对抗样本可以通过逆离散余弦变换(IDCT)转换回输入空间。
搜索候选三角形。 给定一个子空间 St\mathcal{S}_{t}St,候选三角形仅取决于角度 β\betaβ,因为 α\alphaα 在优化过程中会更新。如图 3 所示,如果我们搜索一个角度 β\betaβ 但没有导致一个对抗性的
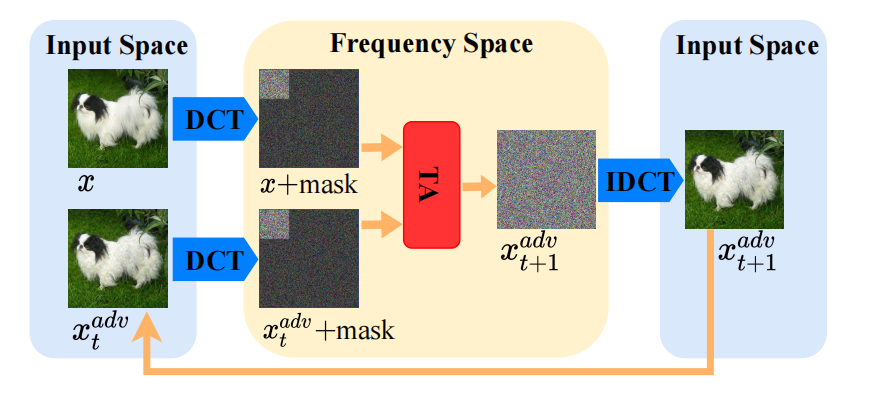
图 2: TA 攻击在第 ttt 次迭代时整个过程的示意图。我们在频率空间中构建三角形以高效地制作对抗样本。请注意,这里我们采用 DCT 进行说明,但我们在每次迭代时不需要对 xxx 使用它。由于 DCT 的一对一映射,我们在频率空间中仍然采用 xxx 和 xtadvx_{t}^{adv}xtadv 而没有歧义。
样本 (xt+1,1adv)(x_{t+1,1}^{adv})(xt+1,1adv),我们可以进一步在相反方向构建一个具有相同角度的对称三角形来检查数据点 xt+1,2advx_{t+1,2}^{adv}xt+1,2adv,该点具有与 xt+1,1advx_{t+1,1}^{adv}xt+1,1adv 相同的扰动幅度但方向不同。我们 unambiguous 地将对称三角形的角度表示为 −β-\beta−β。请注意,在相同角度 α\alphaα 下,较大的角度 β\betaβ 会使第三个顶点更接近输入样本 xxx,即扰动更小。确定子空间 St\mathcal{S}_{t}St 后,我们首先检查角度 βt,0=max(π−2α,β‾)\beta_{t,0}=\max(\pi-2\alpha,\underline{\beta})βt,0=max(π−2α,β),其中 β‾=π/16\underline{\beta}=\pi/16β=π/16 是一个预定义的小角度。如果 T(x,xtadv,αt,βt,0,St)\mathcal{T}(x,x_{t}^{adv},\alpha_{t},\beta_{t,0},\mathcal{S}_{t})T(x,xtadv,αt,βt,0,St) 和 T(x,xtadv,αt,−βt,0,St)\mathcal{T}(x,x_{t}^{adv},\alpha_{t},-\beta_{t,0},\mathcal{S}_{t})T(x,xtadv,αt,−βt,0,St) 都不具有对抗性,我们放弃这个子空间,因为它不能带来任何好处。否则,我们采用二分搜索来找到一个最优角度 β∗∈[max(π−2α,β‾),min(π−α,π/2)]\beta^{*}\in[\max(\pi-2\alpha,\underline{\beta}),\min(\pi-\alpha,\pi/2)]β∗∈[max(π−2α,β),min(π−α,π/2)],该角度尽可能大以最小化扰动。这里我们限制 β\betaβ 的上界,因为对于 β>π/2\beta>\pi/2β>π/2,T(x,xtadv,αt,β,St)\mathcal{T}(x,x_{t}^{adv},\alpha_{t},\beta,\mathcal{S}_{t})T(x,xtadv,αt,β,St) 将位于相对于 xxx 的相反方向,而 π−α\pi-\alphaπ−α 保证了一个有效的三角形。
调整角度 α\alphaα。 直观地说,角度 α\alphaα 平衡了扰动的大小和找到对抗样本的难度:
命题 1。在相同角度 β\betaβ 下,较小的角度 α\alphaα 使得更容易找到对抗样本,而较大的角度 α\alphaα 导致更小的扰动。
直观地,如图 4 所示,较小的角度 α\alphaα 导致较大的扰动但更有可能跨越决策边界,使得更容易搜索对抗样本,反之亦然。很难为每次迭代一致地找到一个最优的 α\alphaα,更不用说各种输入图像和目标模型了。因此,我们根据制作的对抗样本自适应地调整角度 α\alphaα:
αt,i+1={min(αt,i+γ,π/2+τ)if f(xt,i+1adv;θ)≠ymax(αt,i−λγ,π/2−τ)Otherwise\alpha_{t,i+1}=\left\{\begin{array}{ll}\min(\alpha_{t,i}+\gamma,\pi/2+\tau)&\text{if }f(x_{t,i+1}^{adv};\theta)\neq y\\ \max(\alpha_{t,i}-\lambda\gamma,\pi/2-\tau)&\text{Otherwise}\end{array}\right.αt,i+1={min(αt,i+γ,π/2+τ)max(αt,i−λγ,π/2−τ)if f(xt,i+1adv;θ)=yOtherwise (3)
其中 xt,i+1adv=T(x,xtadv,αt,i,βt,i,St)x_{t,i+1}^{adv}=\mathcal{T}(x,x_{t}^{adv},\alpha_{t,i},\beta_{t,i},\mathcal{S}_{t})xt,i+1adv=T(x,xtadv,αt,i,βt,i,St) 是由 αt,i\alpha_{t,i}αt,i 生成的对抗样本,γ\gammaγ 是变化率,λ\lambdaλ 是一个常数,τ\tauτ 限制了 α\alphaα 的上下界。我们采用 λ<1\lambda<1λ<1 来防止角度下降太快,考虑到在扰动优化过程中失败比成功多得多。请注意,较大的角度 α\alphaα 使得更难找到对抗样本。
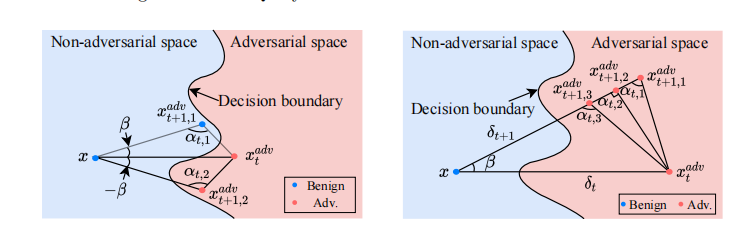
图 3: 对称候选三角形 (xxx, xtadvx_{t}^{adv}xtadv 和 xt+1,2advx_{t+1,2}^{adv}xt+1,2adv) 的示意图。当角度 β\betaβ 不能产生对抗样本 (xt+1,1adv)(x_{t+1,1}^{adv})(xt+1,1adv) 时,我们将进一步基于直线 ⟨x,xtadv⟩\langle x,x_{t}^{adv}\rangle⟨x,xtadv⟩ 构建对称三角形来检查数据点 xt+1,2advx_{t+1,2}^{adv}xt+1,2adv。
图 4: TA 中使用的候选三角形的 α\alphaα 大小的影响。对于相同的采样角度 β\betaβ,较大的角度 α\alphaα 导致更小的扰动,但也更有可能跨越决策边界。
然而,太小的角度 α\alphaα 会导致 β\betaβ 的下界低得多,这也使得 T(x,xtadv,αt,βt,St){\cal T}(x,x_{t}^{adv},\alpha_{t},\beta_{t},{\cal S}_{t})T(x,xtadv,αt,βt,St) 远离当前的对抗样本 xtadvx_{t}^{adv}xtadv,降低了找到对抗样本的概率。因此,我们为 α\alphaα 添加界限以将其限制在适当的范围内。
TA 迭代地从低频空间采样的子空间 St{\cal S}_{t}St 中搜索候选三角形以找到对抗样本并相应地更新角度 α\alphaα。TA 的整个算法总结在算法 1 中。

4 实验
在本节中,我们使用五个模型和腾讯云 API 在标准 ImageNet 数据集上进行了广泛的评估,以评估 TA 的有效性。代码可在 https://github.com/xiaosen-wang/TA 获取。
4.1 实验设置
数据集。 为了验证所提出的 TA 的有效性,遵循 Surface [39] 的设置,我们从 ILSVRC 2012 验证集中随机抽取 200 张正确分类的图像,用于在相应模型上进行评估。
模型。 我们考虑了五个广泛采用的模型,即 VGG-16 [44]、Inception-v3 [45]、ResNet-18 [24]、ResNet-101 [24] 和 DenseNet-121 [25]。为了验证在现实世界中的适用性,我们在腾讯云 API³ 上评估 TA。
³ https://cloud.tencent.com/
基线。 我们将各种基于决策的攻击作为我们的基线,包括四种基于梯度估计的攻击,即 OPT [11]、SignOPT [12]、HSJA [8]、QEBA [29],一种基于优化的攻击,即 BO [43],以及两种受几何启发的攻击,即 GeoDA [38]、Surface [35]。
评估指标。 遵循 QEBA [29] 中的标准设置,我们采用良性样本 xxx 和对抗样本 xadvx^{adv}xadv 之间的均方根误差(RMSERMSERMSE)来衡量扰动的大小:
d(x,xadv)=1w⋅h⋅c∑i=1w∑j=1h∑k=1c(x[i,j,k]−xadv[i,j,k])2,d(x,x^{adv})=\sqrt{\frac{1}{w\cdot h\cdot c}\sum_{i=1}^{w}\sum_{j=1}^{h}\sum_{k=1}^{c}(x[i,j,k]-x^{adv}[i,j,k])^{2}},d(x,xadv)=w⋅h⋅c1i=1∑wj=1∑hk=1∑c(x[i,j,k]−xadv[i,j,k])2, (4)
其中 w,h,cw,h,cw,h,c 分别是输入图像的宽度、高度和通道数。我们还采用攻击成功率,即达到一定距离阈值的对抗样本的百分比。
超参数。 为了公平比较,所有攻击都采用与 [35] 中相同的对抗扰动初始化方法,并且基线的超参数与原始论文完全相同。对于我们的 TA,我们采用每个子空间中的最大迭代次数 N=2N=2N=2,方向线的维度 d=3d=3d=3,以及 γ=0.01\gamma=0.01γ=0.01、λ=0.05\lambda=0.05λ=0.05 和 τ=0.1\tau=0.1τ=0.1 用于更新角度 α\alphaα。
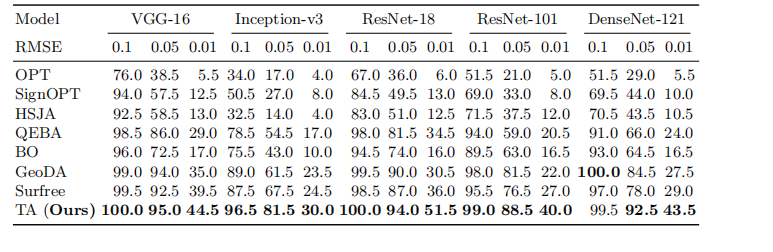
表 1: 在不同 RMSE 阈值下,五个模型上的攻击成功率(%)。最大查询次数设置为 1,000。我们将最高的攻击成功率用粗体标出。
4.2 在标准模型上的评估
为了评估 TA 的有效性,我们首先比较了五种流行模型上不同基于决策攻击的攻击性能,并报告了在各种 RMSERMSERMSE 阈值(即 0.1、0.05 和 0.01)下的攻击成功率。
我们首先评估在 1000 次查询内的攻击,这在最近的工作 [8, 38, 35] 中被广泛采用。攻击成功率总结在表 1 中,这意味着如果攻击花费 1000 次查询仍未达到给定阈值,则攻击将无法为该输入图像生成对抗样本。我们可以观察到,在具有不同架构的五个模型上,在各种扰动预算下,TA 始终比现有的基于决策的攻击实现更好的攻击成功率。例如,在 ResNet-101 上,在 RMSERMSERMSE 阈值为 0.1、0.05、0.01 时,TA 分别以 1.0%、7.5% 和 13.0% 的明显优势优于第二名攻击,ResNet-101 被广泛用于评估基于决策的攻击。特别是,提出的 TA 显著优于两种受几何启发的攻击,即 GeoDA [38] 和 Surface [35],它们在基线中表现出最佳的攻击性能。这令人信服地验证了所提出的 TA 的高效性。此外,在五个模型中,Inception-v3 [46] 在基于决策的攻击中很少被研究,在各种扰动预算下对基线和 TA 都表现出比其他模型更好的鲁棒性。因此,有必要在各种架构上彻底评估基于决策的攻击,而不仅仅是 ResNet 模型。
为了进一步验证 TA 的高效率,我们研究了在 RMSERMSERMSE 阈值分别为 0.1、0.05 和 0.01 时,达到各种攻击成功率所需的查询次数。最大查询次数设置为 10,000,在 ResNet-18 上的结果总结在图 5 中。如图 (a)a 和 (b)b 所示,TA 需要少得多的查询次数来实现 RMSERMSERMSE 阈值为 0.1 和 0.05 的各种攻击成功率,显示了我们方法的高查询效率。对于较小的阈值 0.01,如图 ©c 所示,当攻击成功率低于 50% 时,我们的 TA 仍然需要较少的查询次数,但未能实现高于 60% 的攻击成功率。请注意,如图 6 和表 1 所示,RMSERMSERMSE 阈值为 0.01 非常严格,因此扰动是不可感知的,但也很难为基于决策的攻击生成对抗样本。由于我们主要关注
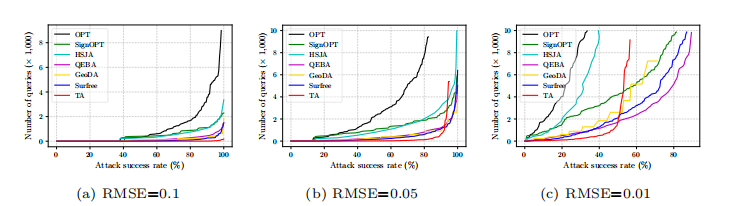
图 5: 在 ResNet-18 上,攻击基线和提出的 TA 在不同扰动预算下达到给定攻击成功率所需的查询次数。最大查询次数为 10,000。
仅基于几何信息的攻击的查询效率,在 RMSERMSERMSE 阈值为 0.01 下的攻击性能是可以接受的,因为在攻击现实世界应用时,如此高的查询次数是不切实际的。
此外,由于 TA 旨在通过利用三角几何来提高查询效率,当允许更多查询时,全局最优可能比现有的基于梯度估计的攻击更差。其他受几何启发的方法在这种情况下没有梯度估计,表现也比 QEBA [29] 差。然而,这不是 TA 的目标,并且可以使用梯度估计轻松解决。借助 TA 的高效率,如果高查询次数是可接受的,我们可以通过将 TA 作为精确梯度估计攻击(如 QEBA [29])的预热来实现更高的攻击性能和更低的查询次数。我们在 2000 次查询后将 QEBA [29] 中使用的梯度估计集成到 TA 中,称为 TAG。对于 0.01 的扰动预算,TAG 使用 7000 次查询实现了 95% 的攻击成功率,这优于使用 9000 次查询实现 92% 攻击成功率的最佳基线。
4.3 在现实世界应用上的评估
随着 DNNs 的卓越性能和前所未有的进步,许多公司已经部署 DNNs 用于各种任务,并为不同的任务提供商业 API(应用程序编程接口)。开发人员可以付费将这些服务集成到他们的应用程序中。然而,DNNs 对对抗样本的脆弱性,特别是基于决策的攻击的繁荣(它不需要目标模型的任何信息),对这些现实世界的应用构成了严重威胁。凭借 TA 的高效率,我们还使用腾讯云 API 验证了其实际攻击适用性。由于商业 API 的高成本,我们从 ImageNet 验证集中随机抽取 20 张图像,最大查询次数为 1000。
成功攻击的图像数量总结在表 2 中。我们可以观察到,在 200、500 和 1000 次查询内,在各种 RMSERMSERMSE 阈值下,TA 成功生成的对抗样本数量多于攻击基线。特别是,我们的 TA 在 500 次查询内生成的对抗样本甚至比最佳攻击基线在 1000 次查询内生成的还要多,显示了 TA 的优越性。我们还在图 6 中可视化了一些由 TA 生成的对抗样本。如我们所见,TA 可以用很少的查询(≤\leq≤ 200)成功地为各种类别生成高质量的对抗样本,验证了 TA 的高适
表 2: 各种攻击基线和提出的 TA 在腾讯云 API 上在 200/500/1000 次查询内成功生成的对抗样本数量。由于在线 API 的高成本,结果是在 ImageNet 中正确分类的图像中随机采样的 20 张图像上评估的。

用性。特别是当查询次数为 200 时,TA 生成的对抗样本对人类来说几乎是视觉上不可察觉的,这突显了当前商业应用的脆弱性。
4.4 消融研究
在本节中,我们在 ResNet-18 上进行了一系列消融研究,即 TA 选择的子空间、低频子空间的比率以及用于更新角度 α\alphaα 的变化率 γ\gammaγ 和 λ\lambdaλ。关于采样线维度 ddd 和 α\alphaα 的界限 τ\tauτ 的参数研究总结在附录 B 中。
关于 TA 选择的子空间。 与现有的基于决策的攻击不同,TA 使用的几何特性的普遍性使得直接在频率空间中优化扰动成为可能。为了研究频率空间的有效性,我们在各种空间中实现了 TA,即输入空间(TAI_{I}I)、在频率空间中采样方向线但在输入空间中优化扰动(TAFI_{\text{FI}}FI)(Surface [35] 使用的方法)和全频率空间(TAF_{\text{F}}F)。如表 3 所示,由于高维输入空间,TAI_{I}I 无法有效探索输入样本的邻域
表 3: 在 ResNet-18 上对不同空间的消融研究,即输入空间(TAI_{I}I)、用于线采样的频率空间但用于扰动优化的输入空间(TAFI_{\text{FI}}FI)以及无掩码的全频率空间(TAF_{\text{F}}F)
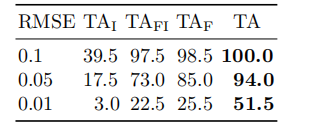

图 6: 由 TA 制作的针对腾讯云 API 的对抗样本。#Q. 表示攻击的查询次数,RMSE 表示良性样本和对抗样本之间的 RMSE 距离。我们在最左列和最右列分别报告了正确标签和预测标签(放大查看细节)。
来找到良好的扰动,并且表现非常差。利用来自频率空间的信息来采样子空间,TAFI_{\rm FI}FI 表现出比 TAI_{\rm I}I 好得多的结果。当在全频率空间中优化扰动时,TAF_{\rm F}F 可以实现比 TAFI_{\rm FI}FI 更高的攻击成功率,显示了频率空间的好处。当使用低频信息采样子空间时,TA 实现了比所有其他攻击好得多的性能,支持了 TA 选择的子空间的必要性和合理性。
关于低频子空间的比率。 低频域在提高 TA 效率方面起着关键作用。然而,没有标准来识别低频,因为它对应于高频,这通常由给定比率的频率域的下部确定。这里我们研究了这个比率对 TA 攻击性能的影响。如图 7 所示,在较小的 RMSERMSERMSE 阈值下,该比率对攻击成功率的影响更显著。通常,增加比率会大致降低攻击性能,因为它使 TA 更关注高频域,而高频域包含的图像关键信息较少。因此,我们采用较低的 10% 部分作为低频子空间以实现高效率,这也有助于 TA 有效降维,使其更容易进行攻击。
关于用于更新角度 α\alphaα 的变化率 γ\gammaγ 和 λ\lambdaλ。 如第 3.3 节所述,角度 α\alphaα 在选择更好的候选三角形方面起着关键作用,但很难为不同的迭代和输入图像找到一个统一的最优 α\alphaα。我们假设较大的角度 α\alphaα 使得更难找到候选三角形,但会导致更小的扰动。如方程(3)所示,如果我们成功找到一个三角形,我们将用 γ\gammaγ 增加 α\alphaα。否则,我们将用 λγ\lambda\gammaλγ 减少 α\alphaα。我们在图 8 中研究了各种 γ\gammaγ 和 λ\lambdaλ 的影响。这里为了清晰起见,我们只报告了 RMSE=0.01RMSE=0.01RMSE=0.01 的结果,RMSE=0.1/0.05RMSE=0.1/0.05RMSE=0.1/0.05 的结果表现出相同的趋势。通常,γ=0.01\gamma=0.01γ=0.01 导致比 γ=0.05/0.005\gamma=0.05/0.005γ=0.05/0.005 更好的攻击性能。当我们在 γ=0.01\gamma=0.01γ=0.01 的情况下增加 λ\lambdaλ 时,攻击成功率增加直到 λ=0.05\lambda=0.05λ=0.05,然后下降。我们还研究了控制方程(3)中 α\alphaα 界限的 τ\tauτ 的影响,它在 1000 次查询内显示出稳定的性能,但在 10000 次查询时生效,我们简单地采用 τ=0.1\tau=0.1τ=0.1。在我们的实验中,我们采用 γ=0.01\gamma=0.01γ=0.01、λ=0.05\lambda=0.05λ=0.05 和 τ=0.1\tau=0.1τ=0.1。
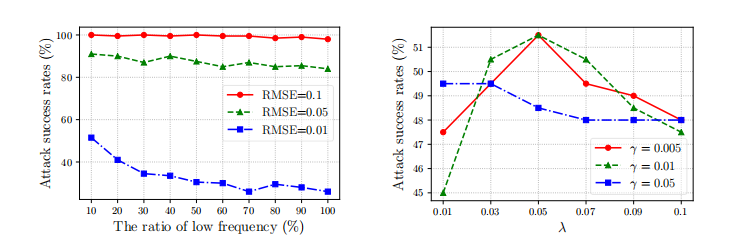
图 7: 在三个 RMSERMSERMSE 阈值下,使用各种低频子空间比率时,TA 在 ResNet-18 上 1000 次查询内的攻击成功率(%)。
图 8: 在 RMSE=0.01RMSE=0.01RMSE=0.01 下,使用各种 γ\gammaγ 和 λ\lambdaλ 更新 α\alphaα 时,TA 在 ResNet-18 上 1000 次查询内的攻击成功率(%)。
4.5 进一步讨论
BoundaryAttack [5] 采用在决策边界上的随机游走来最小化基于决策的攻击的扰动,后续工作通常遵循此设置,将对抗样本限制在决策边界上。我们认为这种限制是不必要的,并且没有在我们的 TA 中采用它。为了验证这一论点,在我们找到候选三角形后,我们还进行了二分搜索以在每次迭代中将对抗样本移向决策边界,以研究这种限制的好处。如图 9 所示,当二分搜索的迭代次数(NbsN_{bs}Nbs)为 000 时,它是普通的 TA,表现出最佳的攻击成功率。当我们增加 NbsN_{bs}Nbs 时,二分搜索在每次迭代中花费更多查询,这降低了给定总查询次数下的总迭代次数。通常,攻击成功率随着 NbsN_{bs}Nbs 的增加而稳定下降,尤其是对于 RMSE=0.01RMSE=0.01RMSE=0.01,这意味着用于将对抗样本限制在决策边界上的二分搜索的成本(即查询)是不值得的。这种限制对于大多数基于决策的攻击,特别是受几何启发的攻击,也可能不可靠和不合理。我们希望这能激发更多关注来讨论将对抗样本限制在决策边界上的必要性,并为设计更强大的基于决策的攻击提供新的思路。
5 结论
在这项工作中,我们发现对于任何迭代攻击,良性样本、当前和下一个对抗样本可以在每次迭代时在子空间中自然地构建一个三角形。基于这一观察,我们提出了一种新颖的基于决策的攻击,称为三角攻击(TA),它利用了几何信息,即在任何三角形中,较长的边对着较大的角。具体来说,在每次迭代中,TA 随机采样一条穿过良性样本的方向线来确定一个子空间,在该子空间中,TA 迭代地搜索候选三角形以最小化对抗扰动。凭借几何特性的普遍性,TA 直接在由 DCT 生成的、维度远低于输入空间的低频空间中优化对抗扰动,并显著提高了查询效率。大量实验表明,TA 在 1000 次查询内实现了更高的攻击成功率,并且达到相同攻击成功率所需的查询次数少得多。在腾讯云 API 上的实际适用性也验证了 TA 的优越性。
致谢
这项工作得到了国家自然科学基金(62076105)、湖北省国际科技合作基金(2021EHB011)和腾讯犀牛鸟精英人才培养计划的支持。
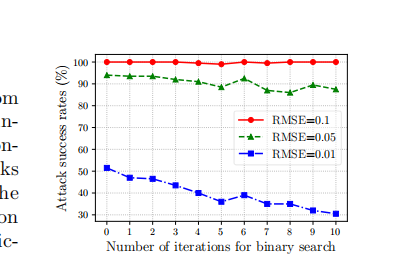
图 9: 使用不同二分搜索迭代次数(NbsN_{bs}Nbs)在每次迭代中将对抗样本限制在决策边界上时,TA 的攻击成功率(%)。
参考文献
-
[1] Nasir Ahmed, T. Natarajan, and Kamisetty R Rao. Discrete cosine transform. IEEE Transactions on Computers, 1974.
-
[2] Abdullah Al-Dujaili and Una-May O’Reilly. Sign bits are all you need for black-box attacks. In International Conference on Learning Representations, 2020.
-
[3] Anish Athalye, Nicholas Carlini, and David A. Wagner. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples. In International Conference on Machine Learning, 2018.
-
[4] Mariusz Bojarski, Davide Del Testa, Daniel Dworakowski, Bernhard Pirner, and Beat Flepp et al. End to end learning for self-driving cars. arXiv preprint arXiv:1604.07316, 2016.
-
[5] Wieland Brendel, Jonas Rauber, and Matthias Bethge. Decision-based adversarial attacks: Reliable attacks against black-box machine learning models. In International Conference on Learning Representations, 2018.
-
[6] Nicholas Carlini and David Wagner. Towards evaluating the robustness of neural networks. In IEEE Symposium on Security and Privacy, 2017.
-
[7] Chenyi Chen, Ari Seff, Alain Kornhauser, and Jianxiong Xiao. Deepdriving: Learning affordance for direct perception in autonomous driving. In International Conference on Computer Vision, pages 2722–2730, 2015.
-
[8] Jianbo Chen, Michael I Jordan, and Martin J Wainwright. Hopskipjumpattack: A query-efficient decision-based attack. In IEEE Symposium on Security and Privacy, 2020.
-
[9] Pin-Yu Chen, Huan Zhang, Yash Sharma, Jinfeng Yi, and Cho-Jui Hsieh. Zoo: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models. In ACM Workshop on Artificial Intelligence and Security, 2017.
-
[10] Weilun Chen, Zhaoxiang Zhang, Xiaolin Hu, and Baoyuan Wu. Boosting decision-based black-box adversarial attacks with random sign flip. In European Conference on Computer Vision, 2020.
-
[11] Minhao Cheng, Thong Le, Pin-Yu Chen, Huan Zhang, Jinfeng Yi, and Cho-Jui Hsieh. Query-efficient hard-label black-box attack: An optimization-based approach. In International Conference on Learning Representations, 2019.
-
[12] Minhao Cheng, Simranjit Singh, Patrick H. Chen, Pin-Yu Chen, Sijia Liu, and Cho-Jui Hsieh. Sign-OPT: A query-efficient hard-label adversarial attack. In International Conference on Learning Representations, 2020.
-
[13] Jeremy M. Cohen, Elan Rosenfeld, and J. Zico Kolter. Certified adversarial robustness via randomized smoothing. In International Conference on Machine Learning, 2019.
-
[14] Francesco Croce and Matthias Hein. Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks. In International Conference on Machine Learning, 2020.
-
[15] Zhongying Deng, Xiaojiang Peng, Zhifeng Li, and Yu Qiao. Mutual component convolutional neural networks for heterogeneous face recognition. IEEE Transactions on Image Processing, 28(6):3102–3114, 2019.
-
[16] Yinpeng Dong, Qi-An Fu, Xiao Yang, Tianyu Pang, Hang Su, Zihao Xiao, and Jun Zhu. Benchmarking adversarial robustness on image classification. In Conference on Computer Vision and Pattern Recognition, 2020.
-
[17] Yinpeng Dong, Fangzhou Liao, Tianyu Pang, Hang Su, Jun Zhu, Xiaolin Hu, and Jianguo Li. Boosting adversarial attacks with momentum. In Conference on Computer Vision and Pattern Recognition, 2018.
-
[18] Jiawei Du, Hu Zhang, Joey Tianyi Zhou, Yi Yang, and Jiashi Feng. Query-efficient meta attack to deep neural networks. In International Conference on Learning Representations, 2020.
-
[19] Kevin Eykholt, Ivan Evtimov, Earlence Fernandes, Bo Li, Amir Rahmati, Chaowei Xiao, Atul Prakash, Tadayoshi Kohno, and Dawn Song. Robust physical-world attacks on deep learning visual classification. In Conference on Computer Vision and Pattern Recognition, 2018.
-
[20] Dihong Gong, Zhifeng Li, Jianzhuang Liu, and Yu Qiao. Multi-feature canonical correlation analysis for face photo-sketch image retrieval. In Proceedings of the 21st ACM International Conference on Multimedia, pages 617–620, 2013.
-
[21] Ian J. Goodfellow, Jonathon Shlens, and Christian Szegedy. Explaining and harnessing adversarial examples. In International Conference on Learning Representations, 2015.
-
[22] Chuan Guo, Jared S Frank, and Kilian Q Weinberger. Low frequency adversarial perturbation. Uncertainty in Artificial Intelligence, 2019.
-
[23] Chuan Guo, Mayank Rana, Moustapha Cisse, and Laurens van der Maaten. Countering adversarial images using input transformations. In International Conference on Learning Representations, 2018.
-
[24] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Conference on Computer Vision and Pattern Recognition, 2016.
-
[25] Gao Huang, Zhuang Liu, Laurens van der Maaten, and Kilian Q. Weinberger. Densely connected convolutional networks. In Conference on Computer Vision and Pattern Recognition, 2017.
-
[26] Andrew Ilyas, Logan Engstrom, Anish Athalye, and Jessy Lin. Black-box adversarial attacks with limited queries and information. In International Conference on Machine Learning, 2018.
-
[27] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E. Hinton. ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems, 2012.
-
[28] Alexey Kurakin, Ian Goodfellow, and Samy Bengio. Adversarial examples in the physical world. In International Conference on Learning Representations, Workshop, 2017.
-
[29] Hutchen Li, Xiaojun Xu, Xiaolu Zhang, Shuang Yang, and Bo Li. QEBA: query-efficient boundary-based blackbox attack. In Conference on Computer Vision and Pattern Recognition, 2020.
-
[30] Zhifeng Li, Dihong Gong, Yu Qiao, and Dacheng Tao. Common feature discriminant analysis for matching infrared face images to optical face images. IEEE Transactions on Image Processing, 23(6):2436–2445, 2014.
-
[31] Siyuan Liang, Baoyuan Wu, Yanbo Fan, Xingxing Wei, and Xiaochun Cao. Parallel rectangle flip attack: A query-based black-box attack against object detection. arXiv preprint arXiv:2201.08970, 2022.
-
[32] Yanpei Liu, Xinyun Chen, Chang Liu, and Dawn Song. Delving into transferable adversarial examples and black-box attacks. In International Conference on Learning Representations, 2017.
-
[33] Yujia Liu, Seyed-Mohsen Moosavi-Dezfooli, and Pascal Frossard. A geometry-inspired decision-based attack. In International Conference on Computer Vision, pages 4890–4898, 2019.
-
[34] Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, and Adrian Vladu. Towards deep learning models resistant to adversarial attacks. In International Conference on Learning Representations, 2018.
-
[35] Thibault Maho, Teddy Furon, and Erwan Le Merrer. SurFree: A fast surrogate-free black-box attack. In Conference on Computer Vision and Pattern Recognition, 2021.
-
[36] Seyed-Mohsen Moosavi-Dezfooli, Alhussein Fawzi, and Pascal Frossard. DeepFool: A simple and accurate method to fool deep neural networks. In Conference on Computer Vision and Pattern Recognition, 2016.
-
[37] Haibo Qiu, Dihong Gong, Zhifeng Li, Wei Liu, and Dacheng Tao. End2end occluded face recognition by masking corrupted features. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021.
-
[38] Ali Rahmati, Seyed-Mohsen Moosavi-Dezfooli, Pascal Frossard, and Huaiyu Dai. GeoDA: a geometric framework for black-box adversarial attacks. In Computer Vision and Pattern Recognition, pages 8446–8455, 2020.
-
[39] Olga Russakovsky, Jia Deng, Hao Su, Jonathan Krause, Sanjeev Satheesh, Sean Ma, Zhiheng Huang, Andrej Karpathy, Aditya Khosla, Michael Bernstein, et al. ImageNet large scale visual recognition challenge. In International booktitle of computer vision, 2015.
-
[40] Ahmad EL Sallab, Mohammed Abdou, Etienne Perot, and Senthil Yogamani. Deep reinforcement learning framework for autonomous driving. Electronic Imaging, 2017(19):70–76, 2017.
-
[41] Ali Shafahi, Mahyar Najibi, Amin Ghiasi, Zheng Xu, John P. Dickerson, Christoph Studer, Larry S. Davis, Gavin Taylor, and Tom Goldstein. Adversarial training for free! In Advances in Neural Information Processing Systems, 2019.
-
[42] Mahmood Sharif, Sruti Bhagavatula, Lujo Bauer, and Michael K Reiter. Accessorize to a crime: Real and stealthy attacks on state-of-the-art face recognition. In ACM SIGSAC conference on Computer and Communications Security, 2016.
-
[43] Satya Narayan Shukla, Anit Kumar Sahu, Devin Willmott, and Zico Kolter. Simple and efficient hard label black-box adversarial attacks in low query budget regimes. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, pages 1461–1469, 2021.
-
[44] Karen Simonyan and Andrew Zisserman. Very deep convolutional networks for large-scale image recognition. In International Conference on Learning Representations, 2015.
-
[45] Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jonathon Shlens, and Zbigniew Wojna. Rethinking the inception architecture for computer vision. In Conference on Computer Vision and Pattern Recognition, 2016.
-
[46] Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jonathon Shlens, and Zbigniew Wojna. Rethinking the inception architecture for computer vision. In Conference on Computer Vision and Pattern Recognition, 2016.
-
[47] Christian Szegedy, Wojciech Zaremba, Ilya Sutskever, Joan Bruna, Dumitru Erhan, Ian J. Goodfellow, and Rob Fergus. Intriguing properties of neural networks. In International Conference on Learning Representations, 2014.
-
[48] Xiaoou Tang and Zhifeng Li. Video based face recognition using multiple classifiers. In IEEE International Conference on Automatic Face and Gesture Recognition, pages 345–349. IEEE, 2004.
-
[49] Chun-Chen Tu, Paishun Ting, Pin-Yu Chen, Sijia Liu, Huan Zhang, Jinfeng Yi, Cho-Jui Hsieh, and Shin-Ming Cheng. Autozoom: Autoencoder-based zeroth order optimization method for attacking black-box neural networks. In AAAI Conference on Artificial Intelligence, 2019.
-
[50] Hao Wang, Yitong Wang, Zheng Zhou, Xing Ji, Dihong Gong, Jingchao Zhou, Zhifeng Li, and Wei Liu. Cosface: Large margin cosine loss for deep face recognition. In Conference on Computer Vision and Pattern Recognition, 2018.
-
[51] Xiaosen Wang and Kun He. Enhancing the transferability of adversarial attacks through variance tuning. In Conference on Computer Vision and Pattern Recognition, 2021.
-
[52] Xiaosen Wang, Xuanran He, Jingdong Wang, and Kun He. Admix: Enhancing the transferability of adversarial attacks. In International Conference on Computer Vision, 2021.
-
[53] Xiaosen Wang, Hao Jin, Yichen Yang, and Kun He. Natural language adversarial defense through synonym encoding. Conference on Uncertainty in Artificial Intelligence, 2021.
-
[54] Xiaosen Wang, Jiadong Lin, Han Hu, Jingdong Wang, and Kun He. Boosting adversarial transferability through enhanced momentum. In British Machine Vision Conference, 2021.
-
[55] Xingxing Wei, Siyuan Liang, Ning Chen, and Xiaochun Cao. Transferable adversarial attacks for image and video object detection. arXiv preprint arXiv:1811.12641, 2018.
-
[56] Yandong Wen, Kaipeng Zhang, Zhifeng Li, and Yu Qiao. A discriminative feature learning approach for deep face recognition. In European Conference on Computer Vision, 2016.
-
[57] Eric Wong, Leslie Rice, and J. Zico Kolter. Fast is better than free: Revisiting adversarial training. In International Conference on Learning Representations, 2020.
-
[58] Boxi Wu, Heng Pan, Li Shen, Jindong Gu, Shuai Zhao, Zhifeng Li, Deng Cai, Xiaofei He, and Wei Liu. Attacking adversarial attacks as a defense. arXiv preprint arXiv:2106.04938, 2021.
-
[59] Weibin Wu, Yuxin Su, Michael R Lyu, and Irwin King. Improving the transferability of adversarial samples with adversarial transformations. In Conference on Computer Vision and Pattern Recognition, 2021.
-
[60] Cihang Xie, Zhishuai Zhang, Yuyin Zhou, Song Bai, Jianyu Wang, Zhou Ren, and Alan L. Yuille. Improving transferability of adversarial examples with input diversity. In Conference on Computer Vision and Pattern Recognition, 2019.
-
[61] Huazhe Xu, Yang Gao, Fisher Yu, and Trevor Darrell. End-to-end learning of driving models from large-scale video datasets. In Conference on Computer Vision and Pattern Recognition, pages 2174–2182, 2017.
-
[62] Xiaolong Yang, Xiaohong Jia, Dihong Gong, Dong-Ming Yan, Zhifeng Li, and Wei Liu. Larnet: Lie algebra residual network for face recognition. In International Conference on Machine Learning, pages 11738–11750. PMLR, 2021.
-
[63] Zhewei Yao, Amir Gholami, Peng Xu, Kurt Keutzer, and Michael W. Mahoney. Trust region based adversarial attack on neural networks. In Conference on Computer Vision and Pattern Recognition, 2019.
-
[64] Hongyang Zhang, Yaodong Yu, Jiantao Jiao, Eric P. Xing, Laurent El Ghaoui, and Michael I. Jordan. Theoretically principled trade-off between robustness and accuracy. In International Conference on Machine Learning, 2019.
-
[65] Pu Zhao, Pin-Yu Chen, Siyue Wang, and Xue Lin. Towards query-efficient black-box adversary with zeroth-order natural gradient descent. In AAAI Conference on Artificial Intelligence, 2020.
附录
这里我们进一步提供了 TA 以及 Surface 在 1000 张图像上的评估,以及对方向线维度 ddd 和角度 α\alphaα 的界限 τ\tauτ 的参数研究。
附录 A 在更多图像上的评估
由于高昂的计算成本,大多数攻击采用数百张图像进行评估(例如,HSJA [8] (100), QEBA [29] (50), GeoDA [38] (350), Surface [35] (200))。我们在实验中遵循 Surface [35] 使用 200 张图像。为了更好地验证 TA 的有效性,我们进一步在 VGG-16 [44] 上使用 1000 张图像比较了 TA 和 Surface [35]。如表 4 所示,在三个 RMSE 阈值下,TA 始终优于 Surface [35],显示了 TA 的优越性。
附录 B 进一步的参数研究
在本节中,我们进一步提供了方向线维度 ddd 和角度 α\alphaα 的界限 τ\tauτ 的参数研究。
关于方向线的维度 ddd。 较小的线维度 ddd 有助于我们在每次迭代中采样多样化的低维空间以提高攻击性能。为了确定 ddd 的一个好值,我们通过将 ddd 从 1 变化到 10 来进行参数研究。如图 10 所示,随着 ddd 持续增加,攻击成功率持续下降,这在 RMSE=0.01RMSE=0.01RMSE=0.01 的设置下最为明显。因此,我们在实验中采用 d=3d=3d=3。
表 4: 在 VGG-16 上使用 1000 张图像在不同 RMSE 阈值下的攻击成功率(%)。最大查询次数设置为 1,000。我们将最高的攻击成功率用粗体标出。
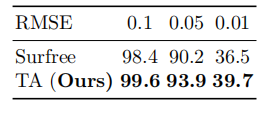
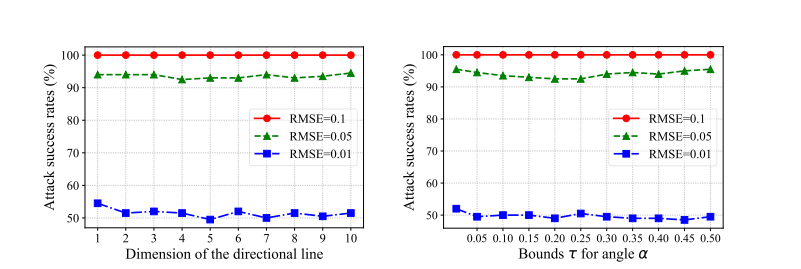
图 10: 在三个 RMSERMSERMSE 阈值下,使用方向线的各种维度时,TA 在 ResNet-18 上 1000 次查询内的攻击成功率(%)。
图 11: 在三个 RMSERMSERMSE 阈值下,使用角度 α\alphaα 的各种界限 τ\tauτ 时,TA 在 ResNet-18 上 1000 次查询内的攻击成功率(%)。
关于角度 α\alphaα 的界限 τ\tauτ。 较小的 α\alphaα 界限 τ\tauτ 会使学习策略无效,而较大的界限可能导致估计不准确,从而降低性能。我们还对 τ\tauτ 进行了参数研究。如图 11 所示,较大的 τ\tauτ 会导致较低的攻击成功率,这在 RMSE=0.01RMSE=0.01RMSE=0.01 时也更明显。因此,我们在实验中采用 τ=0.1\tau=0.1τ=0.1。
