A/B测试：随机化与观察单位不一致，如何处理更科学

本篇文章Clustered Standard Errors in AB Tests适合希望深入理解A/B测试中标准误差调整的读者。文章的亮点在于清晰地解释了当处理单元与观察单元不同时，如何使用聚类稳健标准误差来进行准确推断。作者通过实际案例展示了在客户层面随机化处理时，如何调整标准误差以反映观察值间的相关性，避免了传统方法的低估问题。

---

---

0 笔者自己的理解笔记

0.1 随机化单位，观察单位 是什么？

文章中的一些概念的提及比较费解，而且很多地方我觉得没有说明白，我自己措个笔记：

• 随机化单位：是你决定施加处理（比如显示新功能、提供折扣）的对象。你随机选择这些对象来接受或不接受处理。
• 观察单位：是你收集数据、测量结果的对象。

如何理解呢，文章中提到的“购物车轮播图”例子很形象：

• 场景：一个电商平台想测试在结账页面显示“相关商品轮播图”是否能增加销售额。
• 随机化方式：
  • 错误做法（随机化单位是“订单”）：如果随机决定“每个订单”是否显示轮播图，那么同一个客户可能有时看到轮播图，有时看不到。这会给客户带来混乱的体验，可能影响业务。
  • 正确做法（随机化单位是“客户”）：为了避免上述问题，平台决定随机选择“客户”。一旦一个客户被选中（处理组），他之后的所有订单都会看到轮播图；如果一个客户未被选中（对照组），他之后的所有订单都不会看到轮播图。

观察单位：虽然处理是针对客户进行的，但销售额数据通常是按“订单”来记录的（比如每笔订单的收入）。所以，这里的观察单位是订单。

随机化单位 = 客户；观察单位 = 订单
这就造成了不一致。因为同一个客户下的所有订单都属于同一个处理组，它们之间不再是独立的。

0.2 应对方法

文章提出了几种方法应对以上情况，最主要和推荐的是：

• （1）使用聚类稳健标准误差（Cluster-Robust Standard Errors）：
  这是最直接和常用的方法。它在计算标准误差时，会考虑到同一个“随机化单位”（即“客户”）下的所有“观察单位”（即“订单”）是相互关联的。
  它会调整标准误差，使其能够正确反映这种内部相关性，从而得到更准确的 p 值和置信区间。这样就能避免错误地认为结果显著。

首先，需要明确一点：聚类稳健标准误差并不会改变你计算出的“处理效应”本身的值。 处理效应的点估计（例如，在线性回归中得到的回归系数）仍然是相同的。CRSE 修复的是这个处理效应估计值周围的不确定性，即标准误差，进而影响 p 值和置信区间。
通过这种调整，CRSE 会给出更大、更真实的标准误差。

• 标准误差：不再被低估，更准确地反映了处理效应估计值的真实变异性。
• p 值：会变得更大（更接近真实值），降低了错误判断统计显著性的风险。
• 置信区间：会变得更宽（更接近真实范围），更可靠地包含了处理效应的真实值。
  回到购物车轮播图的例子：

未修复前（使用标准 OLS 标准误差）：
你可能发现轮播图对收入的影响是 -1.63 欧元，p 值为 0.005。你可能会兴奋地认为这个负面影响是统计显著的，并决定取消这个功能。但实际上，这个 p 值可能被低估了。

修复后（使用聚类稳健标准误差）：
当你使用 CRSE 重新计算标准误差时，处理效应的点估计仍然是 -1.63 欧元（因为它不改变系数本身）。但是，标准误差从 0.576 增加到了 2.471。这个更大的标准误差会导致 p 值大幅上升（例如，从 0.005 上升到 0.5）。
现在，你看到 p 值很大，就会意识到这个负面影响在统计上并不显著。你可能就不会轻易取消这个功能，或者会进一步研究。

• （2）自举法（Bootstrapping）：
  通过对“随机化单位”（客户）进行重复抽样，而不是对“观察单位”（订单）进行抽样，来重新计算统计量和标准误差。这种方法也能反映真实的变异性。

关键在于抽样单位：
当随机化单位是“客户”，观察单位是“订单”时，如果进行订单层面的自举（即随机抽订单），那么同一个客户的订单可能被抽到多次，也可能被漏掉，而且不同客户的订单会被视为独立抽样，这仍然会破坏客户内部的相关性结构，导致标准误差依然被低估。
正确的做法是进行聚类层面的自举，也就是以“客户”为单位进行抽样。
步骤：

• 从所有唯一的客户列表中，有放回地随机抽取一批客户（数量与原始客户数相同）。
• 对于每一个被抽到的客户，将其所有相关的订单数据全部包含进来，形成一个新的自举数据集。
• 在这个新的自举数据集上，重新计算处理效应（例如，运行一次 OLS 回归，得到处理系数）。
• 重复步骤 1-3 很多次（比如 1000 次）。

结果：这样就得到了 1000 个处理效应的估计值。这些估计值的标准差，就是处理效应的自举标准误差。

为什么有效：
通过以“客户”为单位抽样，我们保留了每个客户内部所有订单的依赖关系。当一个客户被抽到时，他所有的订单（以及这些订单之间的内在关联）都被完整地带入了自举样本。
不同自举样本之间，处理效应估计值的波动，自然就反映了客户层面的随机性和变异性，这正是我们想要的。它不再假设订单是独立的，而是正确地反映了客户是独立的随机化单位。

优点：

• 灵活性高：不需要像聚类稳健标准误差那样对残差结构做具体假设。
• 直观：通过模拟多次实验来观察估计量的变动。

缺点：

• 计算量大：需要重复运行模型很多次。
• 需要正确实施：必须在正确的聚类层面进行抽样，否则仍然无效。

• （3）聚合数据：
  将数据聚合到“随机化单位”层面。比如，不是分析每个订单的收入，而是计算每个客户的总收入，然后在这个客户层面进行分析。这种方法会损失一些信息，但能确保分析单位的一致性。

核心思想：将观察单位的数据汇总到随机化单位的层面，从而使新的观察单位与随机化单位一致。

如何解决问题：

1. 改变数据结构：

   • 原始数据：每行是一个订单，包含 customer_id, carousel (处理), revenue (结果)。
   • 聚合数据：将每个客户的所有订单数据进行汇总。
     • 例如，计算每个客户的总收入 (customer_total_revenue) 或平均订单收入 (customer_average_revenue)。
     • 新的数据集：每行是一个客户，包含 customer_id, carousel (处理), customer_total_revenue 或 customer_average_revenue。

2. 为什么有效：

   • 单位一致性：现在，你的分析单位变成了“客户”，这与你的随机化单位完全一致。
   • 独立性恢复：由于处理是在客户层面随机分配的，不同的客户之间是相互独立的。一旦你将数据聚合到客户层面，每个客户的汇总数据就成为了一个独立的观察值。
   • 标准方法适用：在新的、以客户为单位的数据集上，你可以直接使用标准的 OLS 回归或其他统计方法。因为新的观察单位（客户）是独立的，所以这些标准方法计算出的标准误差就是正确的，不需要额外的调整。

优点：

• 简单直观：容易理解和操作。
• 标准统计工具直接适用：不需要特殊的 cov_type 参数。

缺点：

• 信息损失：聚合过程会丢失原始订单层面的详细信息。例如，你无法再分析轮播图是否影响了单个订单的商品数量，只能分析它是否影响了客户的总消费。
• 样本量减少：数据集的行数从订单数减少到客户数。这会降低统计功效 (statistical power)，使得检测到真实效应的能力变弱。如果你只有少量客户，这种方法可能效果不佳。
• 加权问题：如果不同客户的订单数量差异很大，简单地聚合可能需要考虑加权回归，以避免订单量大的客户对结果产生过大影响。

0.3 非常简单的举例

好的，我们来举一个电商领域的例子，并说明如何用这三种方法解决。

0.3.1 电商场景示例：新用户引导流程 A/B 测试

背景：一家电商平台希望测试一个新的“新用户引导流程”（例如，注册后的一系列提示和优惠券发放）。他们认为这个新流程能提高新用户的首周购买转化率。

• 随机化单位 (Randomization Unit)：新注册的用户。平台会随机将新注册的用户分配到“旧流程组”（对照组）或“新流程组”（处理组）。一旦用户被分配，他们在实验期间都会体验到对应的流程。
• 观察单位 (Observation Unit)：用户在首周内的每一次“商品浏览事件”。平台记录了每个用户在注册后七天内的所有商品浏览记录，并标记每次浏览是否最终导致了购买（例如，点击商品详情页后是否在同一会话内完成购买）。

问题所在：
一个新用户（随机化单位）在首周内可能会产生多次商品浏览事件（观察单位）。这些来自同一个用户的浏览事件并不是独立的。如果一个用户被分配到新流程组，那么他所有的商品浏览事件都受到了新流程的影响。如果直接用“商品浏览事件”作为分析单位，并使用标准统计方法，就会低估处理效应的标准误差，导致错误地认为新流程显著提升了转化率。

0.3.2 如何用三种方法解决：

在这个新用户引导流程的例子中，无论你选择哪种方法，目标都是为了确保你的统计推断是基于正确的独立性假设，从而避免因数据结构不匹配而得出错误的结论。

0.3.2.1 聚类稳健标准误差 (Cluster-Robust Standard Errors - CRSE)

• 如何操作：
  1. 你仍然会使用“商品浏览事件”作为你的数据行。每行数据包含：user_id (用户ID), is_new_flow (是否在新流程组), is_purchased_after_view (本次浏览是否导致购买)。
  2. 你可以构建一个逻辑回归模型（因为转化率是二元的），或者一个线性概率模型（OLS），来预测 is_purchased_after_view 是否受 is_new_flow 的影响。
  3. 在计算模型的标准误差时，你明确告诉统计软件，要按 user_id 进行聚类。
• 效果：建模后会考虑到同一个 user_id 下的所有浏览事件是相关的，从而调整标准误差。修正后的标准误差会更大，从而得到更准确的 p 值和置信区间，避免错误地判断新流程的转化效果。

0.3.2.2. 自举法 (Bootstrapping)

• 如何操作：
  1. 抽样单位是“用户”：从所有参与实验的新用户列表中，有放回地随机抽取一批用户（数量与原始用户数相同）。
  2. 构建自举数据集：对于每一个被抽到的用户，将其所有在首周内的商品浏览事件数据全部包含进来，形成一个新的自举数据集。
  3. 计算处理效应：在这个自举数据集上，计算新流程对商品浏览后购买转化率的影响（例如，计算处理组和对照组的平均转化率差异）。
  4. 重复多次：重复步骤 1-3 很多次（例如 1000 次），得到 1000 个处理效应的估计值。
  5. 计算标准误差：这 1000 个估计值的标准差，就是处理效应的自举标准误差。
• 效果：通过在用户层面进行抽样，自举法能够准确地捕捉到用户之间的独立性以及用户内部浏览事件的相关性，从而提供一个更可靠的处理效应不确定性度量。

0.3.2.3. 聚合数据 (Aggregating Data)

• 如何操作：
  1. 数据聚合：将每个用户在首周内的所有商品浏览事件进行汇总。
     • 计算每个用户的总浏览次数 (total_views_per_user)。
     • 计算每个用户在浏览后发生的总购买次数 (total_purchases_after_view_per_user)。
     • 然后，计算每个用户的平均浏览后购买转化率 (user_conversion_rate = total_purchases_after_view_per_user / total_views_per_user)。
  2. 新的分析数据集：现在，你的数据集的每一行都是一个用户，包含 user_id, is_new_flow, user_conversion_rate。
  3. 进行标准分析：在这个以用户为单位的数据集上，你可以直接运行标准的线性回归或 t 检验，比较新旧流程组的 user_conversion_rate。
• 效果：由于分析单位（用户）与随机化单位（用户）一致，且用户之间是独立的，因此标准的统计方法计算出的标准误差是有效的。缺点是，你失去了单次浏览事件的细节信息，并且样本量从“浏览事件数”减少到“用户数”，可能会降低你检测到真实效应的能力。

---

1 正文 - 问题提出

1.1 引言

A/B 测试是因果推断的黄金标准，因为它们通过随机化，在最小假设下，允许我们做出有效的因果陈述。事实上，通过随机分配处理（一种药物、广告、产品等），我们能够比较受试者（患者、用户、客户等）的结果（疾病、公司收入、客户满意度等），并将结果的平均差异归因于处理的因果效应。

有时，处理分配单位与观察单位不同。换句话说，我们不是独立地对每个观察单位进行处理决策，而是以组为单位进行。例如，我们可能决定处理某个地区的所有客户，但观察结果是在客户层面；或者处理某个品牌的所有商品，但观察结果是在商品层面。这种情况通常是由于实际限制造成的。在第一个例子中，即所谓的地理实验，由于 cookie 政策的废弃，我们无法跟踪用户。

当这种情况发生时，观察单位之间的处理效应不再独立。事实上，如果一个区域的客户被处理，那么该区域的其他客户也会被处理。如果一个品牌的商品未被处理，那么该品牌的其他商品也不会被处理。在进行推断时，我们必须考虑这种依赖性：标准误差、置信区间和 p 值都应进行调整。在本文中，我们将探讨如何使用聚类稳健标准误差来做到这一点。

1.2 客户、订单与标准误差

想象一下，你是一个在线平台，你对提高销售额很感兴趣。你刚刚有了一个绝妙的主意：在结账时展示一个相关商品轮播图，以鼓励客户将更多商品添加到购物车。为了了解轮播图是否能增加销售额，你决定对其进行 A/B 测试。
原则上，你可以随机决定是否为每个订单显示轮播图。然而，这会给客户带来不一致的体验，可能会损害业务。因此，你决定在客户层面随机分配处理，即轮播图。对于受处理的客户，你会在每个订单中显示轮播图；对于对照组客户，你从不显示轮播图。

我从 src.dgp_collection 导入数据生成过程（DGP），并从 src.theme 导入绘图主题。

%matplotlib inline  
%config InlineBackend.figure_format = 'retina'import numpy as np  
from numpy.linalg import inv  
import pandas as pd  
​  
from src.theme import *  
from src.dgp_collection import dgp_carousel

我们为 3000 个订单生成模拟数据，这些订单来自 100 位客户。对于每个订单，我们观察 order_id（也是数据集索引）、下订单客户的 customer_id、结账时是否显示了 carousel（处理变量）以及订单 revenue（感兴趣的结果变量）。

n = 3000  
dgp = dgp_carousel(n=n, w="carousel", y=["revenue"])  
df = dgp.generate_data()  
df.head()

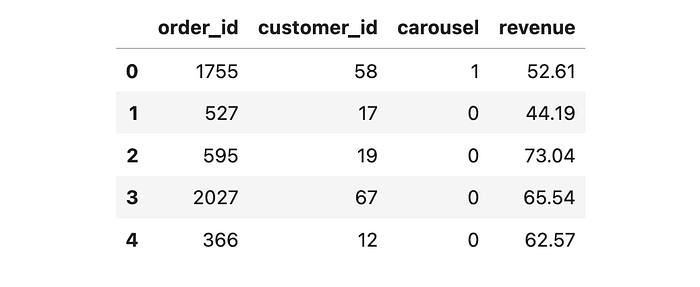
由于处理是随机化的，我们可以通过比较受处理订单的平均收入与对照组（未受处理）订单的平均收入来估计平均处理效应。随机化确保了受处理订单和未受处理订单在平均水平上是可比的，除了处理本身，因此我们可以将任何可观察到的差异归因于处理的因果效应。我们可以使用线性回归来估计均值差异，通过将 revenue 回归到 carousel 虚拟变量上。报告的 OLS 系数就是估计的平均处理效应。

import statsmodels.formula.api as smf  
smf.ols("revenue ~ carousel", data=df).fit().summary().tables[1]

看来包含 carousel 导致每笔订单的 revenue 减少了 \-1.63€。处理效应在 1% 的水平上似乎具有统计显著性，因为报告的 p 值是 0.005。然而，这不是一个标准的 A/B 测试，因为我们没有随机化每个单独的订单，而是随机化了客户。同一客户下的两个订单不可能分到不同的处理组。正因为如此，我们的观察单位之间的处理效应是相关的，而我们计算标准误差时假设它们是独立的。

报告的标准误差是否正确？我们如何“检查”它，以及我们能做些什么？

1.3 标准误差

哪些标准误差是“正确”的？

这个问题的答案取决于我们认为什么是随机的，什么是固定的。在频率学派的意义上，标准误差衡量的是“世界状态”或“平行宇宙”之间的不确定性，这些不确定性会在我们看到数据生成过程的随机部分的不同实现时发生。

在这个特定的案例中，有一个变量是无可争议的随机的：处理分配，事实上，是我们自己随机化的。不仅如此，我们还知道它是如何随机的：每个客户有 50% 的机会看到 carousel，50% 的机会看不到。

因此，我们希望我们估计的标准误差能够衡量在不同处理分配下估计处理效应的变化。这通常是一个抽象概念，因为我们无法重新运行完全相同的实验。然而，在我们的案例中可以，因为我们处于模拟环境中。

DGP 类有一个 evaluate_f_redrawing_assignment 函数，它允许我们通过重新抽样数据并绘制不同的处理分配来评估数据函数 f(X)。我们想要评估的函数是用于处理效应估计的线性回归。

def estimate_treatment_effect(df):  reg = smf.ols("revenue ~ carousel", data=df).fit()  return reg.params["carousel"], reg.bse["carousel"]

我们对 1000 种不同的随机分配重复处理效应估计。

n_draws = 1_000  
ols_coeff = dgp.evaluate_f_redrawing_assignment(f=estimate_treatment_effect, n_draws=n_draws)

在下图中，我们绘制了估计的 OLS 系数和标准误差的分布。在估计标准误差的图中（右侧），我们还报告了一条垂直线，表示模拟中估计系数的标准差（左侧）。

def plot_coefficients(coeffs):  fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5))coeffs_est = list(zip(*coeffs))[0]  sns.histplot(coeffs_est, color="C1", ax=ax1)  ax1.set(title=f"Distribution of estimated coefficients")  ax1.legend([f"Average: {np.mean(coeffs_est):.3f}\nStd. Dev: {np.std(coeffs_est):.3f}"]);  
​  coeffs_std = list(zip(*coeffs))[1]  sns.histplot(coeffs_std, color="C0", ax=ax2)  ax2.set(title=f"Distribution of estimated std. errors")  ax2.legend([f"Average: {np.mean(coeffs_std):.3f}\nStd. Dev: {np.std(coeffs_std):.3f}"]);  ax2.axvline(np.std(coeffs_est), lw=2, ls="--", c="C1")
plot_coefficients(ols_coeff)

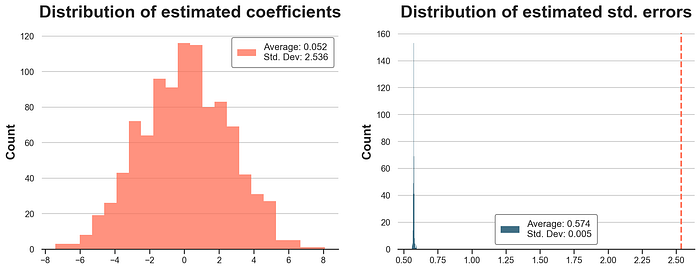
平均系数非常接近零。事实上，真实的处理效应就是零。然而，估计系数的标准差是 2.536，与我们从线性回归表中得到的 0.576 的估计标准差相去甚远。这个标准差将意味着一个大约 0.5 的 p 值，这与任何统计显著性阈值都相距甚远。在右侧面板中，我们看到这并非偶然：标准 OLS 始终低估了系数的变异性约 5 倍。

我们是否可以在现实中检测到这个问题，而无需重新随机化处理分配的可能性？是的，通过自举法（bootstrapping）标准误差。如果你从未听说过自举法，我写了一篇关于它的文章，以及一种使自举法更快有趣的技巧：贝叶斯自举法。

自举法本质上包括有放回地抽取数据样本，并在自举样本中重新计算目标统计量。然后，我们可以通过简单地计算样本中统计量的标准差来估计其标准差。

在这种情况下，重要的是要与数据生成过程一致地对数据进行抽样：按客户而不是按订单。

boot_estimates = []  
customers = df.customer_id.unique()  
for k in range(1000):  np.random.seed(k)  boot_customers = np.random.choice(customers, size=len(customers), replace=True)  df_boot = pd.concat([df[df.customer_id == id] for id in boot_customers])  reg = smf.ols("revenue ~ carousel", data=df_boot).fit()  boot_estimates += [(reg.params["carousel"], reg.bse["carousel"])]

在下图中，我们绘制了估计系数和标准误差的分布。标准误差仍然不正确，但自举估计的分布的标准差为 2.465，非常接近模拟值 2.536。

plot_coefficients(boot_estimates)

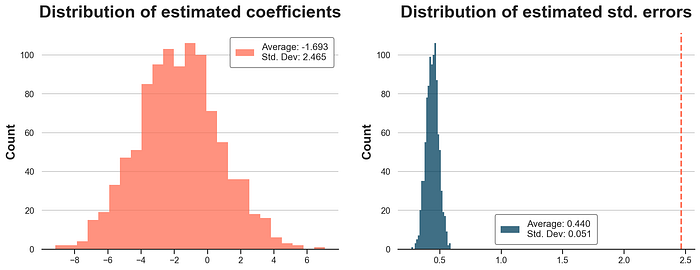
请注意，要使用自举法检测线性回归标准误差中的问题，需要意识到分配是在客户层面进行的。在订单层面进行数据自举仍然会低估标准误差。

2 聚类标准误差

线性回归表中报告的标准误差有什么问题？

问题在于，计算线性回归标准误差的常用公式（稍后会详细介绍数学原理）假设观察值是独立同分布的，即 i.i.d.。然而，在我们的案例中，独立性假设不成立。为什么？

在我们的示例中，处理分配单位（customer）与观察单位（order）不同。这是一个问题，因为在不同的处理分配下，某个客户的所有订单要么都经过处理，要么都没有经过处理。它们是成组移动的，不可能出现同一客户的两个订单分属对照组和处理组的情况。订单“成组移动”的后果是，我们的估计结果的变异性比订单独立移动时更大。直观地说，两个组之间的平衡性平均而言更差。因此，假设独立性计算的标准误差通常会低估估计量的实际变异性。

有解决方案吗？是的！

解决方案是使用所谓的聚类稳健标准误差，它允许观察值在某个观察值聚类（在我们的例子中是 customer）内相关。聚类稳健标准误差通常非常容易实现，并且在所有统计软件包中都可用。使用 statsmodels，我们必须指定协方差类型为 cluster，并且分组依据是 customer。

smf.ols("revenue ~ carousel", data=df).fit(cov_type='cluster', cov_kwds={'groups': df["customer_id"]}).summary().tables[1]

估计的聚类稳健标准误差等于 2.471，与模拟标准误差 2.536 非常接近。请注意，估计系数没有改变（仍然是 \-1.6292）。

聚类稳健标准误差是如何工作的？我们将在下一节深入探讨其数学原理。

2.1 数学原理

OLS 估计量方差的一般公式是

$$Var(\hat{\beta })=(X^{\prime }X{)}^{-1}{X}^{\prime }\Omega X(X^{\prime }X{)}^{-1}$$

其中 [X] 是回归协变量，[\epsilon] 是残差。此公式的关键组成部分是中心矩阵 [n \times n] 矩阵 [\Omega = \epsilon \epsilon’]，其中 [n] 是观察值的数量。它很关键，因为它是我们计算 OLS 估计量方差所需估计的唯一对象。

起初，直接使用回归残差 [e = y - \hat{y}] 来估计 [\Omega] 可能会非常有诱惑力，其中 [y] 是结果向量，[\hat{y}] 是回归预测。然而，问题在于，根据定义，[X] 和 [e] 的乘积为零，因此估计的方差将为零。

X.T @ e

array([[5.72555336e-11],  [6.68904931e-11]])

最简化的假设称为同方差性：回归残差相互独立，并且它们都具有相同的方差。实际上，同方差性意味着 [\Omega] 矩阵是对角线，每个单元格中都有相同的数 ${\sigma }^2$。

$$\Omega ={\sigma }^2{I}_n$$

其中 [I_n] 是维度为 [n] 的单位矩阵。

在同方差性假设下，OLS 方差简化为

$$Var(\hat{\beta })=(X^{\prime }X{)}^{-1}{X}^{\prime }({\sigma }^2{I}_n)X(X^{\prime }X{)}^{-1}={\sigma }^2(X^{\prime }X{)}^{-1}$$

并通过代入残差方差进行估计

y_hat = X @ inv(X.T @ X) @ (X.T @ y)  
e = y - y_hat  
np.var(e)

245.20230307247473

因此，OLS 估计量的估计方差由下式给出

$$\widehat{Var}(\hat{\beta })={\hat{\sigma }}^2(X^{\prime }X{)}^{-1}$$

np.var(e) * inv(X.T @ X)

array([[ 0.14595375, -0.14595375],  [-0.14595375,  0.33171307]])

估计的标准误差只是右下角值的平方根。

np.sqrt(np.var(e) * inv(X.T @ X))[1,1]

0.5759453727032665

计算出的标准误差确实与之前在线性回归表中报告的 0.576 相同。

同方差性是一个非常严格的假设，通常会被放宽，允许不同观察值之间存在不同的残差方差。这个假设被称为异方差性。

$$\Omega =diag({\sigma }_1^2,\dots ,{\sigma }_n^2)$$

在异方差性假设下，OLS 估计量的方差公式不再简化。

Sigma = np.eye(len(df)) * (e @ e.T)  
np.sqrt(inv(X.T @ X) @ X.T @ Sigma @ X @ inv(X.T @ X))[1,1]

0.5757989320663413

在我们的案例中，异方差性下的估计标准误差实际上是相同的：0.576。

在某些情况下，当观察值相关且回归残差不独立时，即使异方差性假设也可能过于严格。在这种情况下，我们可能希望 $\Omega$ 矩阵的某些非对角线元素不为零。但具体是哪些呢？

在许多情况下，包括我们的示例，假设观察值在某些聚类内相关，但具有相同的聚类内方差是合理的。例如，如果聚类是观察对，则$\Omega$ 矩阵采用以下形式。

$$\Omega =\left(\begin{array}{ccccc}{\sigma }^2& \rho {\sigma }^2& 0& 0& \dots \\ \rho {\sigma }^2& {\sigma }^2& 0& 0& \dots \\ 0& 0& {\sigma }^2& \rho {\sigma }^2& \dots \\ 0& 0& \rho {\sigma }^2& {\sigma }^2& \dots \\ ⋮& ⋮& ⋮& ⋮& \ddots \end{array}\right)$$

我们现在可以计算聚类内相关性下的估计标准误差。

customer_id = df[["customer_id"]].values  
Sigma = (customer_id == customer_id.T) * (e @ e.T)  
np.sqrt(inv(X.T @ X) @ X.T @ Sigma @ X @ inv(X.T @ X))[1,1]

2.458350214507729

我们确实得到了线性回归表中报告的相同数字。但是这个公式背后的直观理解是什么？

2.2 直观理解

为了直观理解估计的标准误差，想象我们有一个简单的回归模型，只有一个协变量：一个常数。在这种情况下，OLS 估计量的估计聚类稳健方差就是每个聚类内所有残差交叉乘积的总和。

$$Var(\hat{\beta })=\sum _{g=1}^G\sum _{i=1}^{n_g}\sum _{j=1}^{n_g}{ϵ}_i{ϵ}_j$$

其中 [g] 索引聚类，[n_g] 是聚类 [g] 内观察值的数量。如果观察值独立，则不同观察值残差乘积的期望值是零 $\mathbb{E}[{ϵ}_i{ϵ}_j]=0$，估计的方差将接近平方残差的总和。

$$Var(\hat{\beta })=\sum _{g=1}^G\sum _{i=1}^{n_g}{ϵ}_i^2$$

另一方面，如果观察值高度相关，同一聚类中的残差将非常相似，估计的方差将接近每个聚类中所有交叉乘积的总和。

$$Var(\hat{\beta })=\sum _{g=1}^G{\left(\sum _{i=1}^{n_g}{ϵ}_i\right)}^2$$

这意味着，实际上，如果你的分配单位与观察单位不同，你的有效样本量将介于你的实际样本量和聚类数量（在我们的例子中是客户数量）之间。换句话说，你的数据行数比实际观察值要少。你更接近哪个极端取决于残差的聚类间相关性相对于聚类内相关性的程度。

我们现在可以使用我们的数据生成过程来验证这个直观理解。让我们首先将残差的聚类内方差缩小到零。

dgp = dgp_carousel(n=n, w="carousel", y=["revenue"])  
dgp.revenue_per_customer_std = 0  
df = dgp.generate_data()

现在，未经调整的和聚类的标准误差应该相同，它们确实非常接近。

smf.ols("revenue ~ carousel", data=df).fit().summary().tables[1]

smf.ols("revenue ~ carousel", data=df).fit(cov_type='cluster', cov_kwds={'groups': df["customer_id"]}).summary().tables[1]

现在让我们将跨聚类方差缩小到零。

dgp = dgp_carousel(n=n, w="carousel", y=["revenue"])  
dgp.revenue_std = 0  
df = dgp.generate_data()

在这种情况下，所有方差都在聚类层面，因此标准误差和聚类标准误差之间的差异将更加显著。

smf.ols("revenue ~ carousel", data=df).fit().summary().tables[1]

smf.ols("revenue ~ carousel", data=df).fit(cov_type='cluster', cov_kwds={'groups': df["customer_id"]}).summary().tables[1]

3 结论

在本文中，我们探讨了聚类稳健标准误差的重要性以及它们在随机实验中的相关性。如果你在高于观察单位的层级分配处理，这会在你的观察值的处理效应之间产生相关性，并且使用假设独立性的常用公式计算标准误差可能会严重低估估计量的真实方差。我们探讨了两种解决方案：聚类稳健标准误差和在分配单位层面进行自举的标准误差。

第三种保守的解决方案是在观察单位层面聚合数据。在存在额外非线性协变量的情况下，这将提供标准误差的保守估计。如果每个聚类中的观察值数量不同，我们还需要使用回归权重。

聚类稳健标准误差的一个重要优势是，只有当观察值之间确实存在依赖性时，它们才会比通常的标准误差大。正如我们在最后一节中看到的，如果观察值在聚类之间只有轻微相关，聚类稳健标准误差将非常相似。

4 参考文献

• A. Abadie, S. Athey, G. W. Imbens, J. M. Wooldridge (2023), [When Should You Adjust Standard Errors for Clustering?](https://academic.oup.com/qje/article/138/1/1/675001