灰狼优化算法GWO
0.引言
今天讲一个14年发表在《Advances in Engineering Software》期刊上的论文——Grey Wolf Optimizer。灰狼优化算法是经典的元启发式算法算法之一,比起我之前讲的算法更加复杂和有效。也是前几年比较流行的一个优化算法。
本文主要内容以及主要图片均来源于此论文,想了解论文详情请移步至期刊!
摘要:这项工作提出了一种新的元启发式方法,称为灰狼优化器(GWO),其灵感来自灰狼(Canis lupus)。GWO算法模仿了自然界中灰狼的领导等级和捕猎机制。使用四种类型的灰狼,如阿尔法、贝塔、德尔塔和欧米茄来模拟领导层级。此外,还实施了狩猎、搜索猎物、包围猎物和攻击猎物三个主要步骤。然后,该算法以 29 个众所周知的测试函数为基准,并通过与粒子群优化 (PSO)、引力搜索算法 (GSA)、差分进化 (DE)、进化规划 (EP) 和进化策略 (ES) 的比较研究验证了结果。结果表明,与这些众所周知的元启发式方法相比,GWO 算法能够提供极具竞争力的结果。本文还考虑了解决三个经典工程设计问题(拉伸/压缩弹簧、焊接梁和压力容器设计),并提出了所提方法在光学工程领域的实际应用。经典工程设计问题和实际应用的结果证明,所提算法适用于未知搜索空间的挑战性问题。
1.灵感来源
1.1社会制度
狼群是有社会阶级的,模拟狼群的社会阶级,由高到低将他们分为alphas狼、beta狼、omega狼、delta狼
- alphas狼:是狼群中的头狼,由一雄一雌组成,
- beta狼:贝塔是下属狼,帮助阿尔法进行决策或其他狼群活动。贝塔狼应该尊重阿尔法,但也指挥其他低级狼。
- omega狼:扮演替罪羊的角色。欧米茄狼总是必须屈服于所有其他占主导地位的狼。
- delta狼:必须服从阿尔法和贝塔,但它们主导着欧米茄。通常扮演长者和哨兵的角色。
1.2狩猎行为
①跟踪、追逐和接近猎物。
②追逐、包围和骚扰猎物,直到猎物停止移动。
③向猎物攻击。
2.数学模型
2.1社会层次结构
为了在设计GWO时对狼的社会等级进行数学建模,我们将最优解视为alpha(α)。因此,第二和第三好的解决方案分别命名为beta(β)和delta (δ)。其余的候选解决方案假设为 omega(ω)。在GWO算法中,狩猎(优化)由α、β和δ指导。ω狼跟随这三只狼。
2.2狩猎行为
2.2.1模型
为了对包围行为进行数学建模,提出了以下方程:
其中 t 表示当前迭代,A和C是系数向量,Xp是猎物的位置向量,X表示灰狼的位置向量。
注意:上述不是取模运算,那是逐元素取绝对值。其次也不是点乘,而是逐元素点乘。

其中a在迭代过程中从 2 线性减少到 0,r1,r2是 [0,1] 中的随机向量。
α的模可以用下图表达出来,一条简单的从2到0的直线。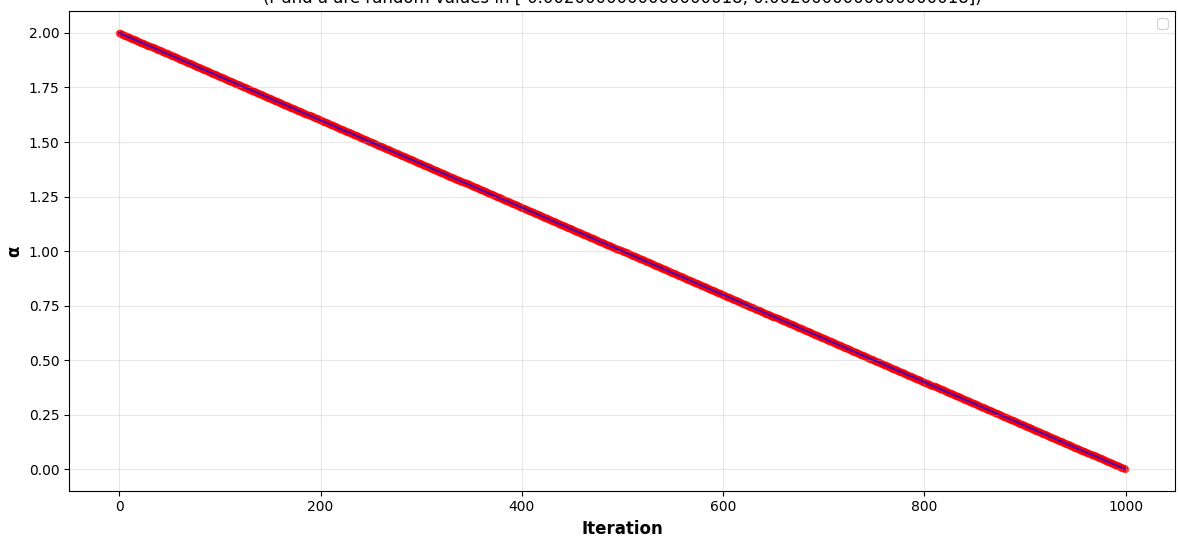
这个公式是整个算法的核心公式,也是最难理解的部分。咱们一步一步来!
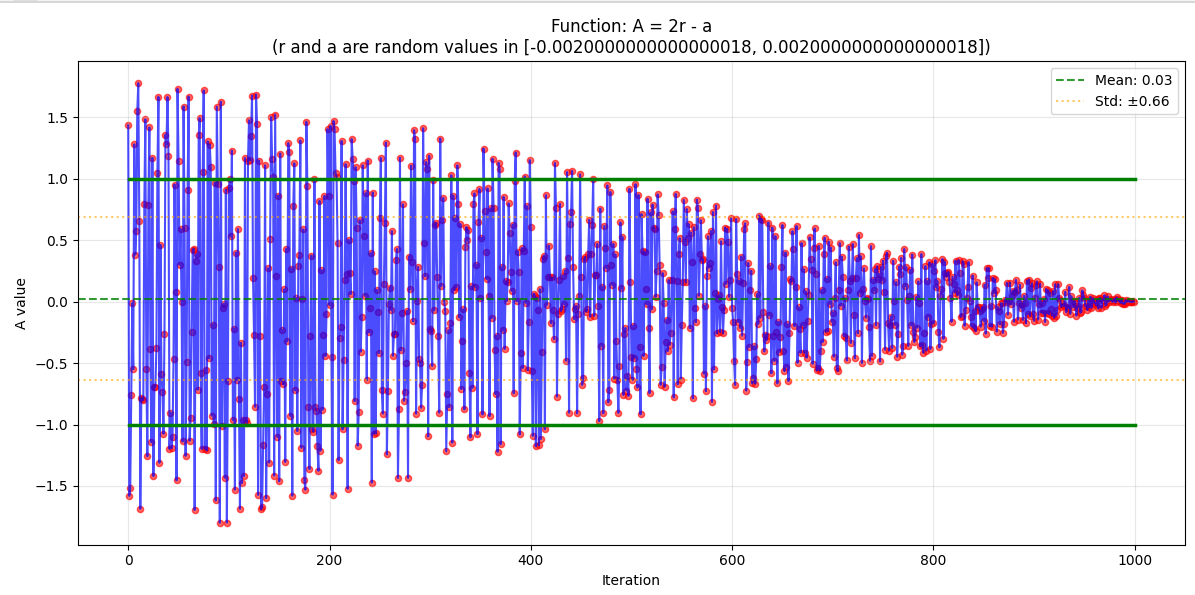
向量A随代数的变换曲线
A的作用是控制算法的模式,是探索模式还是开发模式,换句话说,是全局搜索还是局部搜索。
当A>=1时进入探索阶段。
当A<1时进入开发阶段(上图中绿色的线条用以区分)
可以看出算法从开始到结束全局搜索在逐步减少,直到总代数的一半的时候,停止全局搜索,致力于局部搜索,也就是开发模式。
2.2.2 具体更新方式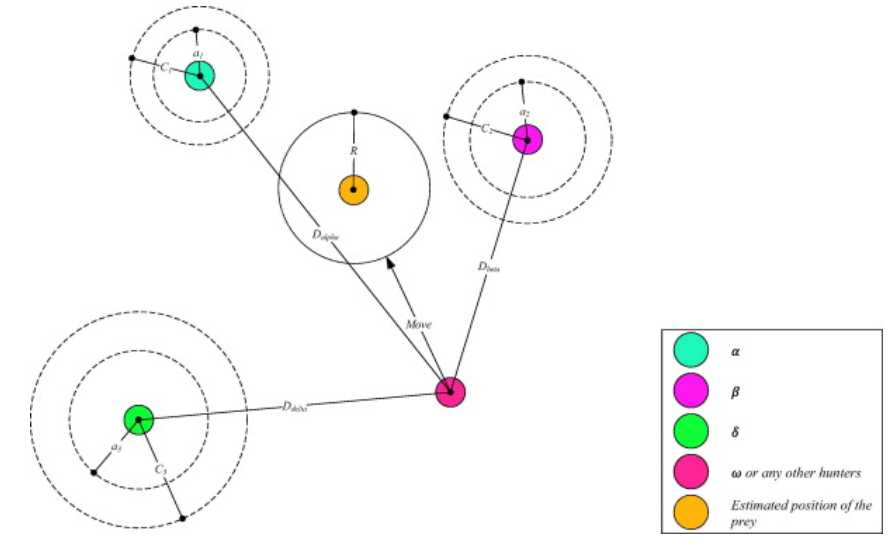
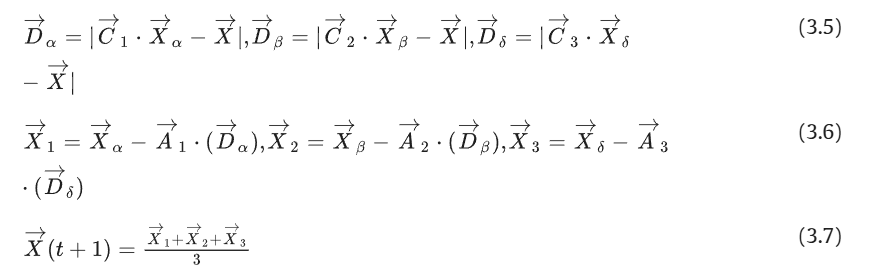
具体一点,就是所有普通狼也就是Ω狼根据以上三个公式更新位置,当所有普通狼更新完位置后,再从中挑选出最优解,次优解,次次优,使之变成α,β,Δ狼。
我们注意到三头首领狼身上都有大圆圈,这是参数C的作用,通过每个维度的逐位相乘,让本来确定的X向量变成一个不确定的大圆圈,增加了算法的随机性。同样参数A也是同理,算出距离向量D后,我们并不想要准确的D的值,而是通过参数A来选择到底是进攻还是包围,换句话说就是通过A来选择到底是局部探索头狼区域还是自由探索。
3.流程
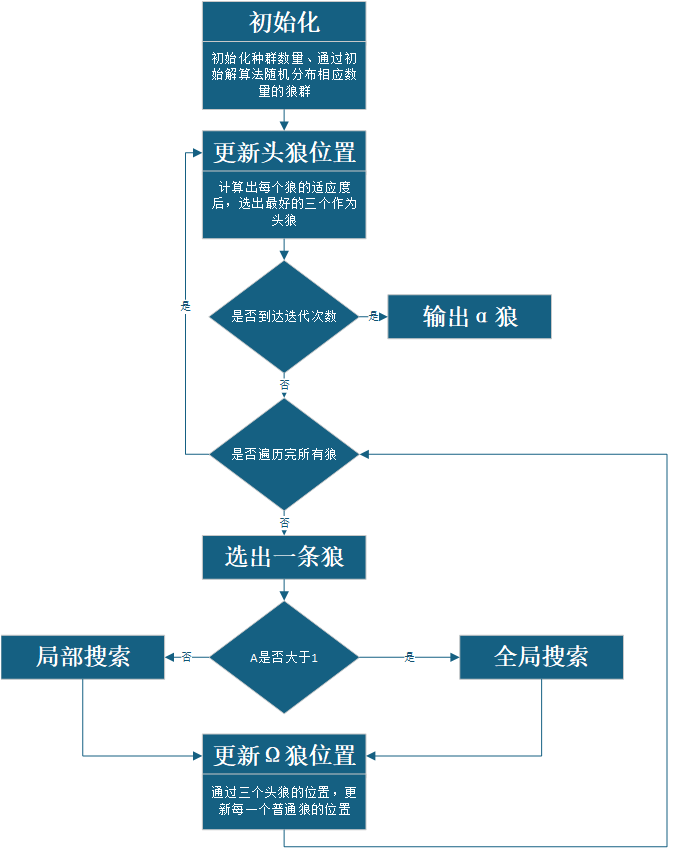

以上是根据我的理解画出的流程图以及原文的伪代码
4解决问题
使用GWO算法,利用python作为工具,解决函数寻优问题。
import numpy as np
import matplotlib.pyplot as plt
import time# 定义测试函数 - Sphere函数(单峰函数)
def sphere_function(x):"""Sphere函数: f(x) = Σ(x_i)^2全局最小值在(0,0,...,0)处,f(0) = 0"""return np.sum(x**2)# 定义测试函数 - Rastrigin函数(多峰函数)
def rastrigin_function(x):"""Rastrigin函数: f(x) = 10*n + Σ[x_i^2 - 10*cos(2πx_i)]全局最小值在(0,0,...,0)处,f(0) = 0"""A = 10return A * len(x) + np.sum(x**2 - A * np.cos(2 * np.pi * x))# 定义测试函数 - Ackley函数(多峰函数)
def ackley_function(x):"""Ackley函数: 复杂的多峰函数全局最小值在(0,0,...,0)处,f(0) = 0"""n = len(x)sum1 = np.sum(x**2)sum2 = np.sum(np.cos(2 * np.pi * x))return -20 * np.exp(-0.2 * np.sqrt(sum1/n)) - np.exp(sum2/n) + 20 + np.e# 灰狼优化算法实现
class GreyWolfOptimizer:def __init__(self, obj_func, dim=2, population_size=30, max_iter=100, search_range=(-10, 10)):"""初始化GWO算法参数:obj_func: 目标函数dim: 问题维度population_size: 种群大小max_iter: 最大迭代次数search_range: 搜索范围"""self.obj_func = obj_funcself.dim = dimself.pop_size = population_sizeself.max_iter = max_iterself.search_range = search_range# 初始化种群self.positions = np.random.uniform(self.search_range[0], self.search_range[1], (self.pop_size, self.dim))# 计算初始适应度self.fitness = np.array([self.obj_func(pos) for pos in self.positions])# 初始化alpha, beta, delta狼self.initialize_leader_wolves()def initialize_leader_wolves(self):"""初始化领导狼(alpha, beta, delta)"""# 按适应度排序sorted_indices = np.argsort(self.fitness)self.alpha_pos = self.positions[sorted_indices[0]].copy()self.alpha_score = self.fitness[sorted_indices[0]]self.beta_pos = self.positions[sorted_indices[1]].copy()self.beta_score = self.fitness[sorted_indices[1]]self.delta_pos = self.positions[sorted_indices[2]].copy()self.delta_score = self.fitness[sorted_indices[2]]def update_a(self, t):"""更新系数a(线性递减从2到0)"""return 2 * (1 - t / self.max_iter)def run(self):"""运行GWO算法"""convergence_curve = []alpha_history = []print("开始GWO优化...")start_time = time.time()for iter in range(self.max_iter):# 更新系数aa = self.update_a(iter)for i in range(self.pop_size):# 对每个维度进行更新new_position = np.zeros(self.dim)for j in range(self.dim):# 为alpha, beta, delta狼计算系数r1 = np.random.random()r2 = np.random.random()A1 = 2 * a * r1 - a # 系数AC1 = 2 * r2 # 系数C# alpha狼的影响D_alpha = abs(C1 * self.alpha_pos[j] - self.positions[i, j])X1 = self.alpha_pos[j] - A1 * D_alpha# beta狼的影响r1 = np.random.random()r2 = np.random.random()A2 = 2 * a * r1 - aC2 = 2 * r2D_beta = abs(C2 * self.beta_pos[j] - self.positions[i, j])X2 = self.beta_pos[j] - A2 * D_beta# delta狼的影响r1 = np.random.random()r2 = np.random.random()A3 = 2 * a * r1 - aC3 = 2 * r2D_delta = abs(C3 * self.delta_pos[j] - self.positions[i, j])X3 = self.delta_pos[j] - A3 * D_delta# 新位置是三个领导狼位置的平均new_position[j] = (X1 + X2 + X3) / 3# 边界检查new_position = np.clip(new_position, self.search_range[0], self.search_range[1])# 计算新位置的适应度new_fitness = self.obj_func(new_position)# 更新狼的位置if new_fitness < self.fitness[i]:self.positions[i] = new_positionself.fitness[i] = new_fitness# 更新领导狼self.update_leader_wolves()# 记录收敛曲线convergence_curve.append(self.alpha_score)alpha_history.append(self.alpha_pos.copy())# 打印进度if iter % 20 == 0 or iter == self.max_iter - 1:print(f'迭代 {iter:3d}: 最佳适应度 = {self.alpha_score:.8f}')end_time = time.time()print(f"\n优化完成!耗时: {end_time - start_time:.2f} 秒")print(f"找到的最佳解: {self.alpha_pos}")print(f"最佳适应度值: {self.alpha_score}")return self.alpha_pos, self.alpha_score, convergence_curve, alpha_historydef update_leader_wolves(self):"""更新领导狼的位置"""# 按适应度排序sorted_indices = np.argsort(self.fitness)# 更新alpha狼if self.fitness[sorted_indices[0]] < self.alpha_score:self.alpha_pos = self.positions[sorted_indices[0]].copy()self.alpha_score = self.fitness[sorted_indices[0]]# 更新beta狼if self.fitness[sorted_indices[1]] < self.beta_score:self.beta_pos = self.positions[sorted_indices[1]].copy()self.beta_score = self.fitness[sorted_indices[1]]# 更新delta狼if self.fitness[sorted_indices[2]] < self.delta_score:self.delta_pos = self.positions[sorted_indices[2]].copy()self.delta_score = self.fitness[sorted_indices[2]]# 可视化结果
def plot_results(convergence_curve, best_positions_history, function_name):"""绘制优化结果"""fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))# 收敛曲线ax1.plot(convergence_curve, 'b-', linewidth=2, label='最佳适应度')ax1.set_xlabel('迭代次数', fontsize=12)ax1.set_ylabel('适应度值', fontsize=12)ax1.set_title(f'{function_name} - 收敛曲线', fontsize=14)ax1.grid(True, alpha=0.3)ax1.legend()# 使用对数坐标(如果值变化很大)if max(convergence_curve) / min(convergence_curve[10:]) > 100:ax1.set_yscale('log')# 最佳位置变化best_positions = np.array(best_positions_history)for dim in range(best_positions.shape[1]):ax2.plot(best_positions[:, dim], label=f'x{dim+1}')ax2.set_xlabel('迭代次数', fontsize=12)ax2.set_ylabel('变量值', fontsize=12)ax2.set_title('最佳位置变化轨迹', fontsize=14)ax2.legend()ax2.grid(True, alpha=0.3)plt.tight_layout()plt.show()# 主函数
def main():# 选择测试函数test_functions = {'Sphere': sphere_function,'Rastrigin': rastrigin_function,'Ackley': ackley_function}print("请选择测试函数:")for i, name in enumerate(test_functions.keys(), 1):print(f"{i}. {name}")choice = int(input("请输入选择 (1-3): ")) - 1function_names = list(test_functions.keys())selected_function = test_functions[function_names[choice]]# 设置算法参数dim = 10 # 问题维度pop_size = 30 # 种群大小max_iter = 100 # 最大迭代次数search_range = (-10, 10) # 搜索范围print(f"\n使用 {function_names[choice]} 函数进行优化...")print(f"问题维度: {dim}, 种群大小: {pop_size}, 最大迭代: {max_iter}")# 运行GWO算法gwo = GreyWolfOptimizer(obj_func=selected_function,dim=dim,population_size=pop_size,max_iter=max_iter,search_range=search_range)best_position, best_score, convergence_curve, alpha_history = gwo.run()# 绘制结果plot_results(convergence_curve, alpha_history, function_names[choice])# 显示统计信息print("\n=== 统计信息 ===")print(f"理论最优值: 0.0")print(f"找到的最优值: {best_score}")print(f"误差: {abs(best_score - 0.0)}")print(f"最终位置: {best_position}")if __name__ == "__main__":main()