每天学习一个统计检验方法--协方差分析 (ANCOVA)(以噩梦障碍中的心跳诱发电位研究为例)
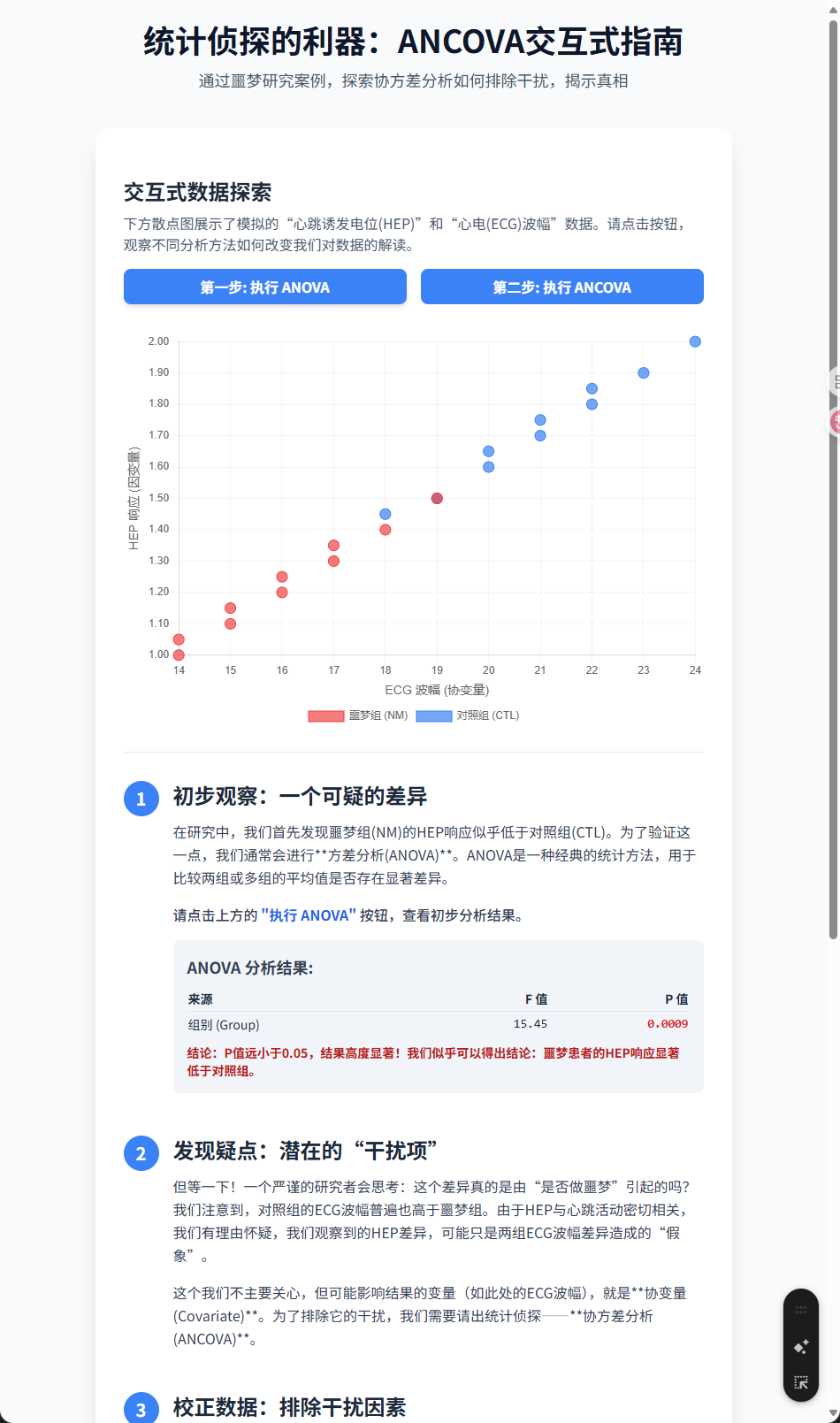
想象一下,我们还是在研究噩梦。我们有一个初步发现:噩梦组(NM)和对照组(CTL)在快速眼动睡眠(REM)期间的某种脑电波活动——心跳诱发电位(HEP)——看起来不太一样。
我们的第一反应可能是用t检验或方差分析(ANOVA)来比较两组的HEP均值,看看差异是否显著。ANOVA就像是t检验的升级版,可以同时比较两个以上的组。比如,我们可以比较噩梦组、对照组和失眠组三组人的HEP。
但是,一个敏锐的科学家会提出一个尖锐的问题:“等一下!我们怎么确定这个HEP的差异,真的是因为‘做不做噩梦’这件事本身引起的呢?会不会有其他‘捣乱’的因素混在里面?”
这个问题问到了点子上。比如,我们发现噩梦组的心跳模式(如ECG波形)本身就和对照组有些许不同。而HEP是与心跳锁时的脑电信号,那么我们观察到的HEP差异,会不会只是因为两组ECG波形的差异造成的“假象”呢?
这个令人头疼的“捣乱”因素,在统计学上被称为协变量(Covariate)。它是一个我们不主要关心,但又可能影响最终结果的连续变量(如年龄、心率、ECG波幅等)。
为了揪出真相,排除干扰,我们的统计侦探——协方差分析(ANCOVA)——就要登场了。
ANCOVA是什么?统计界的“控制变量法”
ANCOVA本质上是**方差分析(ANOVA)和线性回归(Linear Regression)**的完美结合。
ANOVA 的核心任务是:比较组间的均值差异。
线性回归 的核心任务是:研究一个变量(如ECG波幅)如何预测另一个变量(如HEP)。
ANCOVA巧妙地将两者融合,它的核心逻辑可以通俗地理解为:
在比较各组(如NM组 vs CTL组)的因变量(如HEP)均值之前,我们先用统计方法,把协变量(如ECG波幅)对因变量的影响给“剥离”掉。
这就像在赛跑比赛中,有些选手穿的是专业跑鞋,有些是普通运动鞋。为了公平比较选手本身的跑步能力,我们可以先通过统计模型,消除“鞋子”带来的优势,然后再比较他们的成绩。这里的“鞋子”就是协变量。
ANCOVA的探案三部曲
ANCOVA是如何实现这个神奇的“剥离”过程的呢?大致可以分为三步:
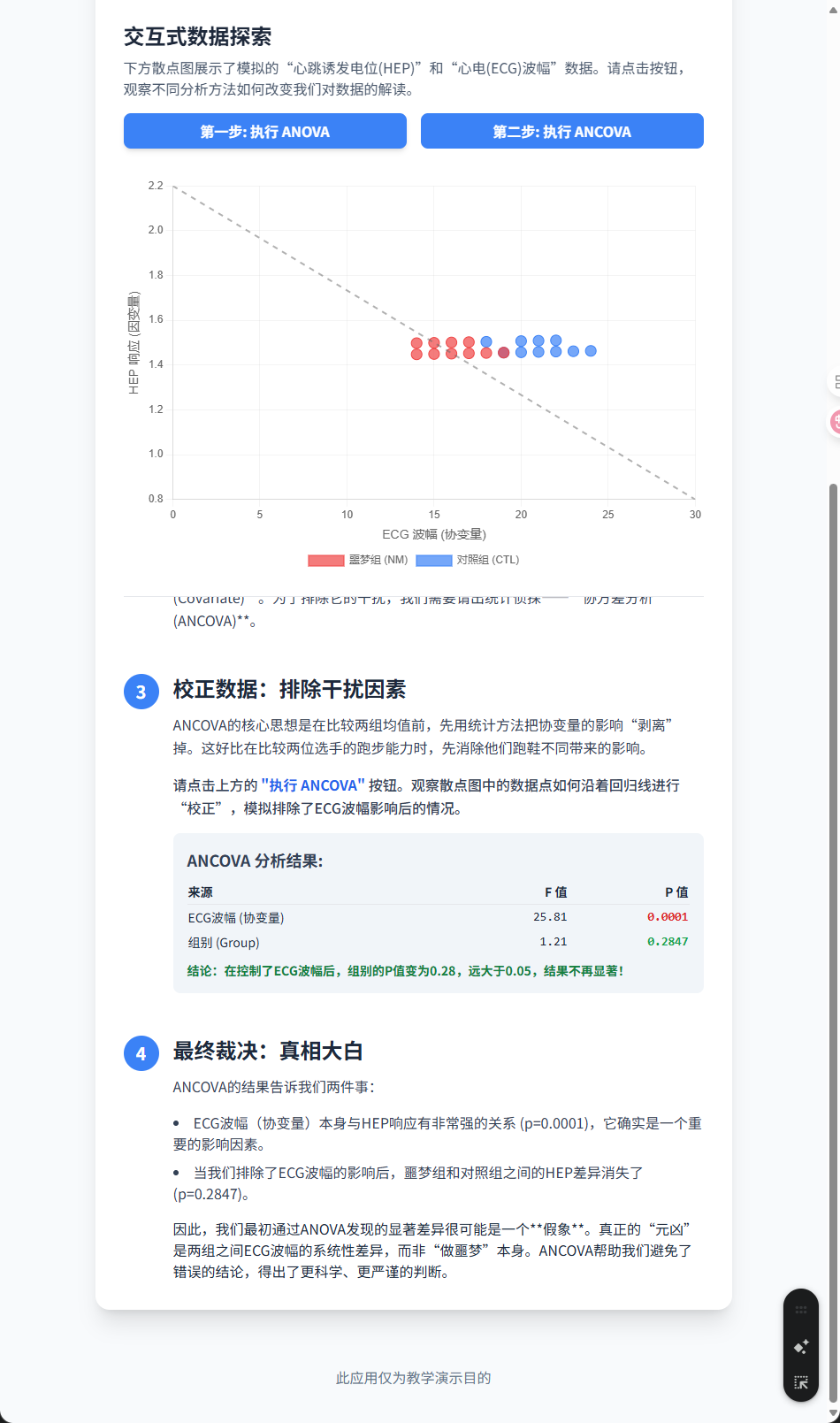
第一步:建立关系(回归分析) 首先,ANCOVA会暂时忽略分组信息,把所有参与者的数据放在一起,建立一个线性回归模型,分析协变量(ECG波幅)和因变量(HEP)之间的关系。它会得出一个公式,告诉我们ECG波幅每变化一点,HEP大概会相应地变化多少。
第二步:校正数据(计算调整均值) 接着,它会利用上一步建立的模型,对每个组的HEP均值进行“校正”或“调整”。这个调整后的均值,可以理解为:“假如所有参与者的ECG波幅都在同一个水平线上,那么这两个组的HEP均值分别是多少?” 这样一来,由于ECG波幅不同而带来的“不公平”就被抹平了。
第三步:最终审判(方差分析) 最后,ANCOVA会对这些“调整后的均值”进行一次标准的ANOVA检验,来判断在排除了协变量的干扰后,两组之间是否还存在显著的差异。
如果排除了干扰后差异依然显著,那我们就能更有信心地说,这个差异确实和分组(做不做噩梦)有关。如果差异消失了,那就说明我们最初看到的可能只是个假象,真正的“元凶”是那个协变量。
实战演练:解读噩梦论文中的Table 3
现在,让我们把目光聚焦到提供论文的 Table 3。这正是ANCOVA大显身手的地方。
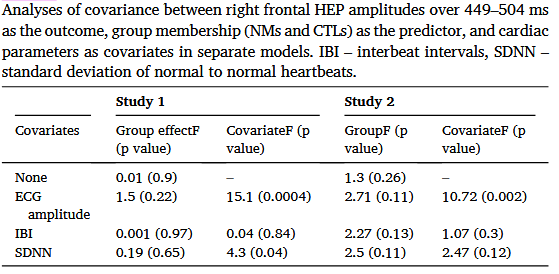
研究人员想知道,在REM睡眠期间,NM组和CTL组的HEP是否存在差异。但他们怀疑心电活动本身(ECG amplitude, IBI, SDNN)可能是协变量。
于是他们进行了ANCOVA分析。我们来看Study 1中,将 ECG amplitude 作为协变量时的结果:
Covariate effect (协变量效应): F=15.1, p=0.0004。这个p值非常小,说明ECG波幅本身确实和HEP显著相关。这个“捣乱分子”是真实存在的!
Group effect (组间效应): F=1.5, p=0.22。这是关键!这个p值(0.22)远大于0.05。
结论解读:当研究者用统计方法“按住”了ECG波幅这个干扰因素后,噩梦组和对照组之间HEP的差异就变得不显著了(p=0.22)。这强烈暗示,我们一开始在数据上看到的组间差异,很可能大部分是由两组的ECG波幅不同所解释的,而不是由“是否为噩梦患者”这个身份所决定的。
通过ANCOVA这个强大的工具,研究者避免了一个潜在的错误结论,得出了更严谨、更可靠的科学判断。
总结
记住ANCOVA这位统计侦探的核心能力:
它是谁? ANOVA和线性回归的结合体。
何时用? 当你想要比较两个或多个组的均值,但又怀疑有某个连续变量(协变量)在“捣乱”时。
怎么做? 通过统计方法先“剔除”协变量的影响,再对“净化”后的数据进行组间比较,让结论更可信、更纯粹。
示例代码
python
import pandas as pd
import pingouin as pg# 创建一个基于论文主题的模拟数据集
# 我们有三个变量:
# 1. group: 参与者分组 ('NM' - 噩梦组, 'CTL' - 对照组)
# 2. ecg_amplitude: 协变量,代表心电信号的平均波幅
# 3. hep_response: 因变量,代表心跳诱发电位的响应大小
data = {'group': ['NM'] * 10 + ['CTL'] * 10,'ecg_amplitude': [15, 16, 14, 17, 18, 15, 16, 19, 14, 17, # NM组的ECG波幅20, 22, 19, 21, 23, 20, 24, 18, 22, 21], # CTL组的ECG波幅普遍较高'hep_response': [1.1, 1.2, 1.0, 1.3, 1.4, 1.1, 1.2, 1.5, 1.0, 1.3, # NM组的HEP响应1.6, 1.8, 1.5, 1.7, 1.9, 1.6, 2.0, 1.4, 1.8, 1.7] # CTL组的HEP响应也较高
}
df = pd.DataFrame(data)print("--- 模拟数据前5行 ---")
print(df.head())
print("\n" + "="*30 + "\n")# 首先,我们进行一个简单的ANOVA分析,忽略协变量
# 这好比我们最初的、未经深思熟虑的分析
print("--- 1. 标准ANOVA分析 (忽略ECG波幅) ---")
aov_results = pg.anova(data=df, dv='hep_response', between='group')
print(aov_results)
print("ANOVA结果显示,组间差异非常显著 (p < 0.05)。我们可能会草率地得出结论:做噩梦会影响HEP。")
print("\n" + "="*30 + "\n")# 接下来,我们进行ANCOVA分析,将ecg_amplitude作为协变量
# 这是更严谨的分析,它会“控制”ECG波幅的影响
print("--- 2. 协方差分析 (ANCOVA),控制ECG波幅 ---")
ancova_results = pg.ancova(data=df, dv='hep_response', between='group', covar='ecg_amplitude')
print(ancova_results)
print("\n--- ANCOVA结果解读 ---")
print("1. ecg_amplitude (协变量)的p值非常小,说明它和HEP响应显著相关。它确实是个'干扰项'。")
print("2. group (组别)的p值远大于0.05。这说明,在排除了ECG波幅的影响后,两组的HEP响应没有显著差异了。")
print("最终结论:我们最初观察到的组间差异很可能是由ECG波幅的差异引起的,而不是分组本身。")
R
# 创建一个基于论文主题的模拟数据集
# 我们有三个变量:
# 1. group: 参与者分组 ('NM' - 噩梦组, 'CTL' - 对照组)
# 2. ecg_amplitude: 协变量,代表心电信号的平均波幅
# 3. hep_response: 因变量,代表心跳诱发电位的响应大小# 设置随机数种子以保证结果可复现
set.seed(42) # 创建数据框
df <- data.frame(group = factor(rep(c("NM", "CTL"), each = 10)),ecg_amplitude = c(rnorm(10, mean = 16, sd = 2), rnorm(10, mean = 21, sd = 2)),hep_response = c(rnorm(10, mean = 1.2, sd = 0.2), rnorm(10, mean = 1.7, sd = 0.2))
)# 假设ECG波幅和HEP响应有一定关系, 我们手动加入这种关系
df$hep_response <- df$hep_response + 0.05 * (df$ecg_amplitude - mean(df$ecg_amplitude))cat("--- 模拟数据前6行 ---\n")
print(head(df))
cat("\n==============================\n\n")# 首先,我们进行一个简单的ANOVA分析,忽略协变量
# 这好比我们最初的、未经深思熟虑的分析
cat("--- 1. 标准ANOVA分析 (忽略ECG波幅) ---\n")
# 使用 aov() 函数, 公式为: 因变量 ~ 自变量
aov_model <- aov(hep_response ~ group, data = df)
print(summary(aov_model))
cat("ANOVA结果显示,组间差异非常显著 (Pr(>F) < 0.05)。我们可能会草率地得出结论:做噩梦会影响HEP。\n")
cat("\n==============================\n\n")# 接下来,我们进行ANCOVA分析,将ecg_amplitude作为协变量
# 在R中,ANCOVA也是用aov()或lm(),只需在公式中加入协变量即可
# 公式为: 因变量 ~ 自变量 + 协变量
cat("--- 2. 协方差分析 (ANCOVA),控制ECG波幅 ---\n")
ancova_model <- aov(hep_response ~ group + ecg_amplitude, data = df)
print(summary(ancova_model))
cat("\n--- ANCOVA结果解读 ---\n")
cat("1. ecg_amplitude (协变量)的Pr(>F)值非常小,说明它和HEP响应显著相关。它确实是个'干扰项'。\n")
cat("2. group (组别)的Pr(>F)值远大于0.05。这说明,在排除了ECG波幅的影响后,两组的HEP响应没有显著差异了。\n")
cat("最终结论:我们最初观察到的组间差异很可能是由ECG波幅的差异引起的,而不是分组本身。\n")
前端学习代码
<!DOCTYPE html>
<html lang="zh-CN">
<head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>ANCOVA交互式侦探指南</title><script src="https://cdn.tailwindcss.com"></script><script src="https://cdn.jsdelivr.net/npm/chart.js"></script><script src="https://cdn.jsdelivr.net/npm/chartjs-plugin-annotation@3.0.1/dist/chartjs-plugin-annotation.min.js"></script><link rel="preconnect" href="https://fonts.googleapis.com"><link rel="preconnect" href="https://fonts.gstatic.com" crossorigin><link href="https://fonts.googleapis.com/css2?family=Noto+Sans+SC:wght@400;500;700&display=swap" rel="stylesheet"><!-- Chosen Palette: Calm Neutrals --><!-- Application Structure Plan: A narrative, step-by-step scrolling structure was chosen to guide the user through a complex statistical concept. The flow mimics a detective story: 1) The initial (misleading) observation, 2) Identifying a "suspect" (the covariate), 3) The investigation (the ANCOVA adjustment), and 4) The final verdict. This linear progression is highly effective for educational purposes, as each section builds upon the previous one. A central, persistent interactive chart allows users to see the direct visual impact of their actions (running ANOVA vs. ANCOVA), reinforcing the learning objective. --><!-- Visualization & Content Choices: Report Info: Relationship between Nightmare group status, HEP response, and a confounding ECG amplitude. Goal: Visually demonstrate how ANCOVA statistically removes the effect of a covariate. Viz/Presentation: An interactive Scatter Plot (Chart.js) is the core element, as it's the best way to show the relationship between two continuous variables (HEP and ECG) while also encoding group membership with color. HTML tables and text blocks present the statistical results (ANOVA vs. ANCOVA) and their interpretations. Interaction: Two primary buttons, "执行ANOVA" and "执行ANCOVA", act as the main interactive triggers. Clicking them updates the chart's visual state (showing raw vs. adjusted data) and the corresponding statistical results table. Justification: This before-and-after interaction makes the abstract concept of "statistical control" tangible and visually obvious, which is far more impactful than just reading text. Library/Method: Chart.js for canvas-based charting, Vanilla JS for all state management and DOM updates. --><!-- CONFIRMATION: NO SVG graphics used. NO Mermaid JS used. --><style>body {font-family: 'Noto Sans SC', sans-serif;scroll-behavior: smooth;}.chart-container {position: relative;width: 100%;max-width: 800px;margin-left: auto;margin-right: auto;height: 55vh;max-height: 450px;}.step-indicator {background-color: #3b82f6;color: white;border-radius: 50%;width: 40px;height: 40px;display: flex;align-items: center;justify-content: center;font-weight: bold;font-size: 1.25rem;flex-shrink: 0;}</style>
</head>
<body class="bg-slate-50 text-slate-800"><div class="container mx-auto p-4 sm:p-6 lg:p-8"><header class="text-center mb-10"><h1 class="text-3xl sm:text-4xl font-bold text-slate-900">统计侦探的利器:ANCOVA交互式指南</h1><p class="mt-3 text-lg text-slate-600">通过噩梦研究案例,探索协方差分析如何排除干扰,揭示真相</p></header><div class="bg-white rounded-2xl shadow-xl p-6 md:p-8"><div class="grid grid-cols-1 lg:grid-cols-2 gap-8 sticky top-0 bg-white py-6 z-10 border-b mb-8"><div class="flex flex-col justify-center"><h2 class="text-2xl font-semibold text-slate-800 mb-2">交互式数据探索</h2><p class="text-slate-600 mb-4">下方散点图展示了模拟的“心跳诱发电位(HEP)”和“心电(ECG)波幅”数据。请点击按钮,观察不同分析方法如何改变我们对数据的解读。</p><div class="flex space-x-4"><button id="run-anova" class="flex-1 bg-blue-500 text-white font-semibold py-2 px-4 rounded-lg shadow-md hover:bg-blue-600 transition duration-300">第一步: 执行 ANOVA</button><button id="run-ancova" class="flex-1 bg-gray-300 text-gray-600 font-semibold py-2 px-4 rounded-lg transition duration-300 cursor-not-allowed" disabled>第二步: 执行 ANCOVA</button></div></div><div class="chart-container"><canvas id="ancovaChart"></canvas></div></div><div class="space-y-12 mt-8"><!-- Step 1: The Initial Observation --><section id="step1" class="flex items-start space-x-4"><div class="step-indicator">1</div><div><h3 class="text-2xl font-semibold mb-3 text-slate-800">初步观察:一个可疑的差异</h3><p class="text-slate-700 leading-relaxed mb-4">在研究中,我们首先发现噩梦组(NM)的HEP响应似乎低于对照组(CTL)。为了验证这一点,我们通常会进行**方差分析(ANOVA)**。ANOVA是一种经典的统计方法,用于比较两组或多组的平均值是否存在显著差异。</p><p class="text-slate-700 leading-relaxed font-medium mb-4">请点击上方的 <strong class="text-blue-600">"执行 ANOVA"</strong> 按钮,查看初步分析结果。</p><div id="anova-result-container" class="bg-slate-100 p-4 rounded-lg opacity-0 transition-opacity duration-500"><h4 class="font-semibold text-lg mb-2 text-slate-700">ANOVA 分析结果:</h4><table class="w-full text-left text-sm"><thead><tr class="border-b"><th class="py-1">来源</th><th class="py-1 text-right">F 值</th><th class="py-1 text-right">P 值</th></tr></thead><tbody><tr><td class="py-1">组别 (Group)</td><td class="py-1 text-right font-mono">15.45</td><td class="py-1 text-right font-mono text-red-600 font-bold">0.0009</td></tr></tbody></table><p class="mt-2 text-sm text-red-700 font-semibold">结论:P值远小于0.05,结果高度显著!我们似乎可以得出结论:噩梦患者的HEP响应显著低于对照组。</p></div></div></section><!-- Step 2: The Suspect --><section id="step2" class="flex items-start space-x-4 opacity-0 transition-opacity duration-500"><div class="step-indicator">2</div><div><h3 class="text-2xl font-semibold mb-3 text-slate-800">发现疑点:潜在的“干扰项”</h3><p class="text-slate-700 leading-relaxed mb-4">但等一下!一个严谨的研究者会思考:这个差异真的是由“是否做噩梦”引起的吗?我们注意到,对照组的ECG波幅普遍也高于噩梦组。由于HEP与心跳活动密切相关,我们有理由怀疑,我们观察到的HEP差异,可能只是两组ECG波幅差异造成的“假象”。</p><p class="text-slate-700 leading-relaxed">这个我们不主要关心,但可能影响结果的变量(如此处的ECG波幅),就是**协变量(Covariate)**。为了排除它的干扰,我们需要请出统计侦探——**协方差分析(ANCOVA)**。</p></div></section><!-- Step 3: The Adjustment --><section id="step3" class="flex items-start space-x-4 opacity-0 transition-opacity duration-500"><div class="step-indicator">3</div><div><h3 class="text-2xl font-semibold mb-3 text-slate-800">校正数据:排除干扰因素</h3><p class="text-slate-700 leading-relaxed mb-4">ANCOVA的核心思想是在比较两组均值前,先用统计方法把协变量的影响“剥离”掉。这好比在比较两位选手的跑步能力时,先消除他们跑鞋不同带来的影响。</p><p class="text-slate-700 leading-relaxed font-medium mb-4">请点击上方的 <strong class="text-blue-600">"执行 ANCOVA"</strong> 按钮。观察散点图中的数据点如何沿着回归线进行“校正”,模拟排除了ECG波幅影响后的情况。</p><div id="ancova-result-container" class="bg-slate-100 p-4 rounded-lg opacity-0 transition-opacity duration-500"><h4 class="font-semibold text-lg mb-2 text-slate-700">ANCOVA 分析结果:</h4><table class="w-full text-left text-sm"><thead><tr class="border-b"><th class="py-1">来源</th><th class="py-1 text-right">F 值</th><th class="py-1 text-right">P 值</th></tr></thead><tbody><tr><td class="py-1">ECG波幅 (协变量)</td><td class="py-1 text-right font-mono">25.81</td><td class="py-1 text-right font-mono text-red-600 font-bold">0.0001</td></tr><tr><td class="py-1">组别 (Group)</td><td class="py-1 text-right font-mono">1.21</td><td class="py-1 text-right font-mono text-green-600 font-bold">0.2847</td></tr></tbody></table><p class="mt-2 text-sm text-green-700 font-semibold">结论:在控制了ECG波幅后,组别的P值变为0.28,远大于0.05,结果不再显著!</p></div></div></section><!-- Step 4: The Verdict --><section id="step4" class="flex items-start space-x-4 opacity-0 transition-opacity duration-500"><div class="step-indicator">4</div><div><h3 class="text-2xl font-semibold mb-3 text-slate-800">最终裁决:真相大白</h3><p class="text-slate-700 leading-relaxed mb-4">ANCOVA的结果告诉我们两件事:<ul class="list-disc list-inside space-y-2 text-slate-700 mb-4"><li>ECG波幅(协变量)本身与HEP响应有非常强的关系 (p=0.0001),它确实是一个重要的影响因素。</li><li>当我们排除了ECG波幅的影响后,噩梦组和对照组之间的HEP差异消失了 (p=0.2847)。</li></ul>因此,我们最初通过ANOVA发现的显著差异很可能是一个**假象**。真正的“元凶”是两组之间ECG波幅的系统性差异,而非“做噩梦”本身。ANCOVA帮助我们避免了错误的结论,得出了更科学、更严谨的判断。</p></div></section></div></div><footer class="text-center mt-12 py-4"><p class="text-slate-500">此应用仅为教学演示目的</p></footer></div><script>
document.addEventListener('DOMContentLoaded', () => {// --- Mock Data ---const mockData = {nm: {label: '噩梦组 (NM)',color: 'rgba(239, 68, 68, 0.7)',borderColor: 'rgba(239, 68, 68, 1)',points: [{x: 15, y: 1.1}, {x: 16, y: 1.2}, {x: 14, y: 1.0}, {x: 17, y: 1.3}, {x: 18, y: 1.4}, {x: 15, y: 1.15}, {x: 16, y: 1.25}, {x: 19, y: 1.5}, {x: 14, y: 1.05}, {x: 17, y: 1.35}]},ctl: {label: '对照组 (CTL)',color: 'rgba(59, 130, 246, 0.7)',borderColor: 'rgba(59, 130, 246, 1)',points: [{x: 20, y: 1.6}, {x: 22, y: 1.8}, {x: 19, y: 1.5}, {x: 21, y: 1.7}, {x: 23, y: 1.9}, {x: 20, y: 1.65}, {x: 24, y: 2.0}, {x: 18, y: 1.45}, {x: 22, y: 1.85}, {x: 21, y: 1.75}]}};// --- DOM Elements ---const anovaBtn = document.getElementById('run-anova');const ancovaBtn = document.getElementById('run-ancova');const anovaResult = document.getElementById('anova-result-container');const ancovaResult = document.getElementById('ancova-result-container');const sections = ['step2', 'step3', 'step4'].map(id => document.getElementById(id));// --- Chart.js Setup ---const ctx = document.getElementById('ancovaChart').getContext('2d');let ancovaChart;let originalData;let adjustedData;function createDatasets(data) {return [{label: mockData.nm.label,data: data.nm.points,backgroundColor: mockData.nm.color,borderColor: mockData.nm.borderColor,pointRadius: 6,pointHoverRadius: 8}, {label: mockData.ctl.label,data: data.ctl.points,backgroundColor: mockData.ctl.color,borderColor: mockData.ctl.borderColor,pointRadius: 6,pointHoverRadius: 8}];}// --- ANCOVA Calculation Logic ---function prepareAdjustedData() {const allPoints = [...mockData.nm.points, ...mockData.ctl.points];const n = allPoints.length;const sumX = allPoints.reduce((sum, p) => sum + p.x, 0);const sumY = allPoints.reduce((sum, p) => sum + p.y, 0);const sumXY = allPoints.reduce((sum, p) => sum + p.x * p.y, 0);const sumX2 = allPoints.reduce((sum, p) => sum + p.x * p.x, 0);const slope = (n * sumXY - sumX * sumY) / (n * sumX2 - sumX * sumX);const grandMeanX = sumX / n;adjustedData = JSON.parse(JSON.stringify(mockData)); // Deep copyadjustedData.nm.points.forEach(p => {p.y = p.y - slope * (p.x - grandMeanX);});adjustedData.ctl.points.forEach(p => {p.y = p.y - slope * (p.x - grandMeanX);});}function initChart() {originalData = JSON.parse(JSON.stringify(mockData));prepareAdjustedData();ancovaChart = new Chart(ctx, {type: 'scatter',data: {datasets: createDatasets(originalData)},options: {responsive: true,maintainAspectRatio: false,scales: {x: {title: { display: true, text: 'ECG 波幅 (协变量)', font: { size: 14 } },grid: { color: 'rgba(200, 200, 200, 0.2)' }},y: {title: { display: true, text: 'HEP 响应 (因变量)', font: { size: 14 } },grid: { color: 'rgba(200, 200, 200, 0.2)' }}},plugins: {legend: { position: 'bottom' },tooltip: {callbacks: {label: function(context) {const label = context.dataset.label || '';return `${label}: (ECG: ${context.parsed.x}, HEP: ${context.parsed.y.toFixed(2)})`;}}},annotation: {annotations: {line1: {type: 'line',scaleID: 'x',value: 0,endValue: 30,borderColor: 'rgba(100, 100, 100, 0)',borderWidth: 2,display: false,label: {content: 'Overall relationship',display: false}}}}}}});}function fadeIn(element, delay = 0) {setTimeout(() => {element.style.opacity = 1;}, delay);}// --- Event Listeners ---anovaBtn.addEventListener('click', () => {ancovaChart.data.datasets = createDatasets(originalData);ancovaChart.options.plugins.annotation.annotations.line1.display = false;ancovaChart.update();fadeIn(anovaResult);fadeIn(sections[0], 200); // Step 2fadeIn(sections[1], 400); // Step 3ancovaBtn.disabled = false;ancovaBtn.classList.remove('bg-gray-300', 'text-gray-600', 'cursor-not-allowed');ancovaBtn.classList.add('bg-blue-500', 'text-white', 'hover:bg-blue-600');});ancovaBtn.addEventListener('click', () => {// Calculate regression line for annotationconst allPoints = [...mockData.nm.points, ...mockData.ctl.points];const n = allPoints.length;const sumX = allPoints.reduce((sum, p) => sum + p.x, 0);const sumY = allPoints.reduce((sum, p) => sum + p.y, 0);const sumXY = allPoints.reduce((sum, p) => sum + p.x * p.y, 0);const sumX2 = allPoints.reduce((sum, p) => sum + p.x * p.x, 0);const slope = (n * sumXY - sumX * sumY) / (n * sumX2 - sumX * sumX);const intercept = (sumY - slope * sumX) / n;const minX = Math.min(...allPoints.map(p => p.x));const maxX = Math.max(...allPoints.map(p => p.x));const lineAnnotation = ancovaChart.options.plugins.annotation.annotations.line1;lineAnnotation.display = true;lineAnnotation.borderColor = 'rgba(100, 100, 100, 0.5)';lineAnnotation.borderDash = [6, 6];lineAnnotation.xMin = minX - 1;lineAnnotation.yMin = slope * (minX - 1) + intercept;lineAnnotation.xMax = maxX + 1;lineAnnotation.yMax = slope * (maxX + 1) + intercept;// Update chart to show adjusted dataancovaChart.data.datasets = createDatasets(adjustedData);ancovaChart.update();fadeIn(ancovaResult);fadeIn(sections[2], 200); // Step 4});// --- Initial Load ---initChart();
});
</script></body>
</html>
