当前位置：首页 > news >正文

701. 二叉搜索树中的插入操作

news 2025/9/21 12:45:28

题目链接：

题目：

解题思路：

代码：

总结：

题目链接：

701. 二叉搜索树中的插入操作 - 力扣（LeetCode）

题目：

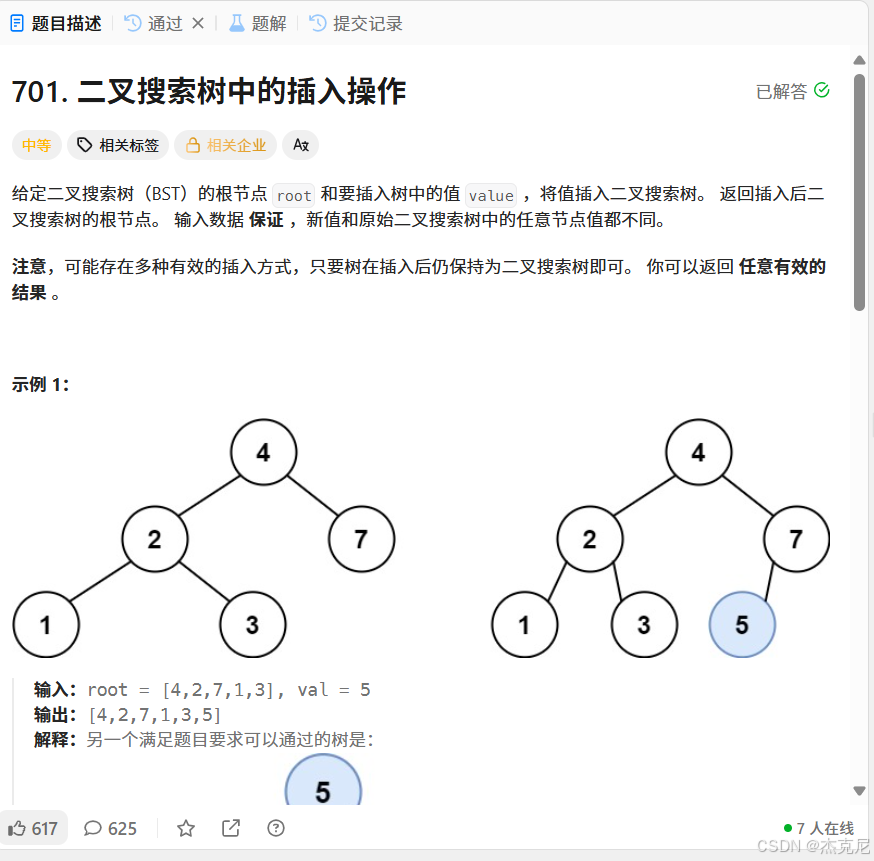
解题思路：

搜索树递归就行,使用的搜索一条边即可,若root.val<val，右递归,否则,左递归。

代码：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode insertIntoBST(TreeNode root, int val) {if(root==null){TreeNode node=new TreeNode(val);return node;}if(root.val>val){root.left= insertIntoBST(root.left,val);}else if(root.val<val){root.right= insertIntoBST(root.right,val);} return root;}
}

二叉搜索树插入操作的递归实现详解在二叉搜索树（Binary Search Tree，BST）的相关操作中，插入操作是最基础且重要的操作之一。本文将详细解析一段用于向二叉搜索树中插入新节点的递归代码，帮助读者深入理解其原理、执行过程以及二叉搜索树的特性。二叉搜索树的基本概念二叉搜索树是一种特殊的二叉树，它具有以下特性：若左子树不为空，则左子树上所有节点的值均小于根节点的值。若右子树不为空，则右子树上所有节点的值均大于根节点的值。左、右子树也分别为二叉搜索树。这种特性使得二叉搜索树能够支持高效的查找、插入和删除操作，时间复杂度在平均情况下为 \(O(\log n)\)（n 为节点数），在理想的平衡状态下，性能接近二分查找。代码整体结构java运行/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if(root==null){
TreeNode node=new TreeNode(val);
return node;
}
if(root.val>val){
root.left= insertIntoBST(root.left,val);
}else if(root.val<val){
root.right= insertIntoBST(root.right,val);
}
return root;
}
}
这段代码的核心是 insertIntoBST 方法，它接收当前二叉搜索树的根节点 root 和要插入的值 val，并返回插入新节点后的二叉搜索树的根节点。关键代码逐行解析递归终止条件java运行if(root==null){
TreeNode node=new TreeNode(val);
return node;
}
这是递归的终止条件。当 root 为 null 时，说明已经遍历到了合适的插入位置（即可以在当前位置插入新节点）。此时，创建一个值为 val 的新节点 node，并返回该节点。这个新节点将作为其父节点的左子节点或右子节点（取决于父节点的值与 val 的大小关系）。递归选择子树java运行if(root.val>val){
root.left= insertIntoBST(root.left,val);
}
如果当前根节点 root 的值大于要插入的值 val，根据二叉搜索树的特性，val 应该插入到 root 的左子树中。所以，递归调用 insertIntoBST 方法，参数为 root.left（当前根节点的左子节点）和 val，并将返回的结果赋值给 root.left。这样，新节点就会被插入到左子树的正确位置，同时更新了当前根节点的左子节点引用。java运行else if(root.val<val){
root.right= insertIntoBST(root.right,val);
}
如果当前根节点 root 的值小于要插入的值 val，同理，val 应该插入到 root 的右子树中。递归调用 insertIntoBST 方法，参数为 root.right 和 val，并将返回的结果赋值给 root.right，完成新节点在右子树的插入和引用更新。返回根节点java运行return root;
在完成左子树或右子树的插入操作后，返回当前的根节点 root。这一步非常重要，因为它保证了在递归过程中，每一层的根节点都能正确地将子树的引用传递给上一层，从而维护整个二叉搜索树的结构完整性。算法执行流程示例为了更好地理解代码的执行过程，我们通过一个具体的例子来模拟插入操作。假设初始的二叉搜索树结构如下（根节点值为 5，左子节点为 3，右子节点为 7）：plaintext 5
/ \
3 7
现在要插入值为 4 的节点。调用 insertIntoBST(root, 4)，其中 root 是值为 5 的节点。因为 5 > 4，所以进入左子树的递归调用：insertIntoBST(root.left, 4)，此时 root.left 是值为 3 的节点。在 insertIntoBST(root.left, 4) 中，root 是值为 3 的节点。因为 3 < 4，所以进入右子树的递归调用：insertIntoBST(root.right, 4)，此时 root.right 为 null。在 insertIntoBST(null, 4) 中，触发终止条件，创建值为 4 的新节点，并返回该节点。回到上一层（值为 3 的节点的右子树插入调用），将返回的新节点（值为 4）赋值给 root.right（值为 3 的节点的右子节点）。此时，值为 3 的节点的右子节点变为值为 4 的节点。返回值为 3 的节点，回到最上层（值为 5 的节点的左子树插入调用），将返回的值为 3 的节点（已更新右子节点为 4）赋值给 root.left（值为 5 的节点的左子节点）。最终返回值为 5 的节点，此时二叉搜索树的结构变为：plaintext 5
/ \
3 7
\
4
时间复杂度与空间复杂度时间复杂度该算法的时间复杂度为 \(O(h)\)，其中 h 是二叉搜索树的高度。在理想情况下，二叉搜索树是平衡的，高度 \(h = \log n\)（n 为节点数），此时时间复杂度为 \(O(\log n)\)。但在最坏情况下，二叉搜索树可能退化为链表（例如，所有节点都只有右子节点），此时高度 \(h = n\)，时间复杂度为 \(O(n)\)。空间复杂度空间复杂度为 \(O(h)\)，主要是由递归调用栈的深度决定的。递归调用的深度最多为二叉搜索树的高度 h，所以在理想情况下空间复杂度为 \(O(\log n)\)，最坏情况下为 \(O(n)\)。总结这段用于向二叉搜索树中插入新节点的递归代码，巧妙地利用了二叉搜索树的特性，通过递归的方式，在合适的位置插入新节点，同时保持二叉搜索树的结构不变。其核心思想是：根据当前节点值与插入值的大小关系，选择左子树或右子树进行递归插入操作，直到找到空的位置，创建新节点并完成插入。理解这段代码，不仅有助于掌握二叉搜索树的插入操作，也能加深对递归算法和二叉搜索树特性的理解，为后续学习二叉搜索树的其他操作（如查找、删除）以及更复杂的树结构（如平衡二叉树）打下基础。

总结：

本文详细解析了二叉搜索树(BST)的递归插入实现。通过递归方法，根据当前节点值与插入值的大小关系选择左/右子树继续查找，直到找到空位创建新节点。代码时间复杂度为O(h)，h为树高，空间复杂度同样为O(h)。该算法充分利用BST的特性，在保持树结构的同时高效完成插入操作，是理解BST基础操作的重要示例。

查看全文

http://www.dtcms.com/a/393195.html