当前位置： 首页 > news >正文

C++哈希进阶：位图与布隆过滤器+海量信息处理

news 2025/9/21 8:30:15

        前面我们已经学习了哈希表的相关内容，本期就让我们进一步深入学习哈希的进阶用法：位图与布隆过滤器，以及关于海量数据处理的应用。

        本期内容相关代码已经上传至作者的个人gitee：楼田莉子/CPP代码学习喜欢请点个赞谢谢

目录

位图

        位图的设计及其实现

        代码实现：

STL：bitset介绍

        引用

        构造函数

        操作符重载

        访问

        []运算符重载

        size

        count

        test  ​编辑

        any

        none

        all

        位运算

        set

        reset

        flip

        位操作

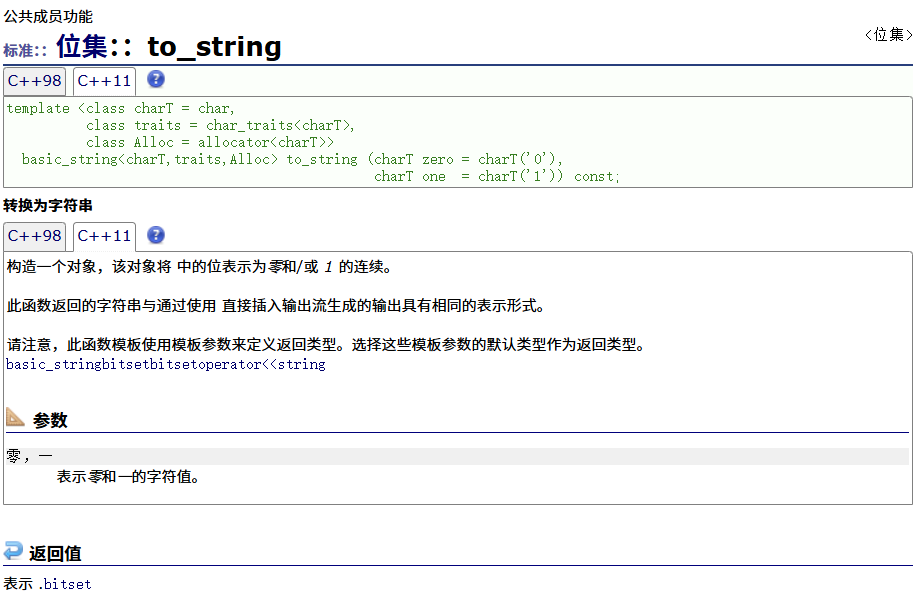
        to_string

​编辑

        to_ulong

        to_ullong

        非成员函数操作符重载

        类模板实例化

        位图的优缺点

考察题目

布隆过滤器

        什么是布隆过滤器

布隆过滤器器误判率推导     

布隆过滤器的实现

布隆过滤器删除问题

布隆过滤器的优缺点

布隆过滤器的应用

海量信息处理问题        

        10亿个整数里面最大的前100个。

        位图相关的面试题

        给两个文件，分别有100亿个query（查询），我们只有1G内存，如何找到两个文件交 集？

        给⼀个超过100G⼤⼩的logfile,log中存着ip地址,设计算法找到出现次数最 多的ip地址？查找出现次数前10的ip地址

位图

        位图的设计及其实现

        位图本质是⼀个直接定址法的哈希表，每个整型值映射⼀个bit位，位图提供控制这个bit的相关接⼝。

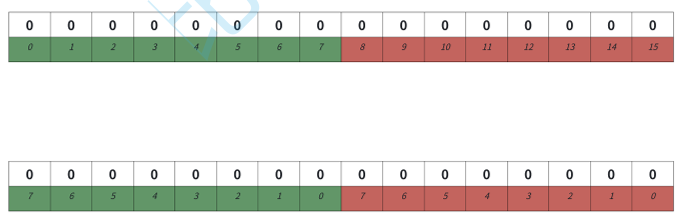
        实现中需要注意的是，C/C++没有对应位的类型，只能看int/char这样整形类型，我们再通过位运算去 控制对应的⽐特位。⽐如我们数据存到vector中，相当于每个int值映射对应的32个值，⽐如第⼀ 个整形映射0-31对应的位，第⼆个整形映射32-63对应的位，后⾯的以此类推，那么来了⼀个整形值 x，i=x/32；j=x%32；计算出x映射的值在vector的第i个整形数据的第j位。

        解决给40亿个不重复的⽆符号整数，查找⼀个数据的问题，我们要给位图开2^32个位，注意不能开40 亿个位，因为映射是按⼤⼩映射的，我们要按数据⼤⼩范围开空间，范围是是0-2^32-1，所以需要开 2^32个位。然后从⽂件中依次读取每个set到位图中，然后就可以快速判断⼀个值是否在这40亿个数中了

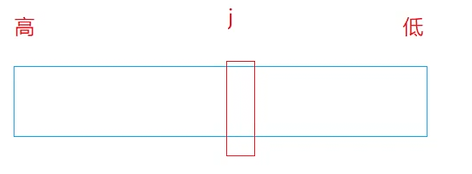
        左移不是方向，是低位向高位移动

        代码实现：

        BitSet.h

#pragma once
#include <vector>
namespace The_Song_of_the_end_of_the_world
{//N表示需要多少比特位template<size_t N>class BitSet{public:BitSet(){_bits.resize(N / 32 + 1);}//x映射的位置标记为1void set(size_t x){size_t i = x / 32;size_t j = x % 32;_bits[i] |= ((size_t)1 << j);}//x映射的位置标记为0void reset(size_t x){size_t i = x / 32;size_t j = x % 32;_bits[i] &= (~(size_t)1 << j);}//x映射的位置为1则返回真，否则返回假bool test(size_t x){size_t i = x / 32;size_t j = x % 32;return _bits[i] & (1 << j);}private:std::vector<size_t> _bits;};
}

        test.cpp

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include<Bitset>
#include"bitset.h"
using namespace std;
void test()
{The_Song_of_the_end_of_the_world::BitSet<100> bs;bs.set(32);bs.set(33);bs.reset(34);cout << bs.test(32) << endl;cout << bs.test(33) << endl;cout << bs.test(34) << endl;
}
//解决问题
void test2()
{The_Song_of_the_end_of_the_world::BitSet<-1> bs;// 开2 ^ 32位的位图    //bit::bitset<-1> bs2;//bit::bitset<UINT_MAX> bs3;//bit::bitset<0xffffffff> bs4;
}
int main()
{test();return 0;
}

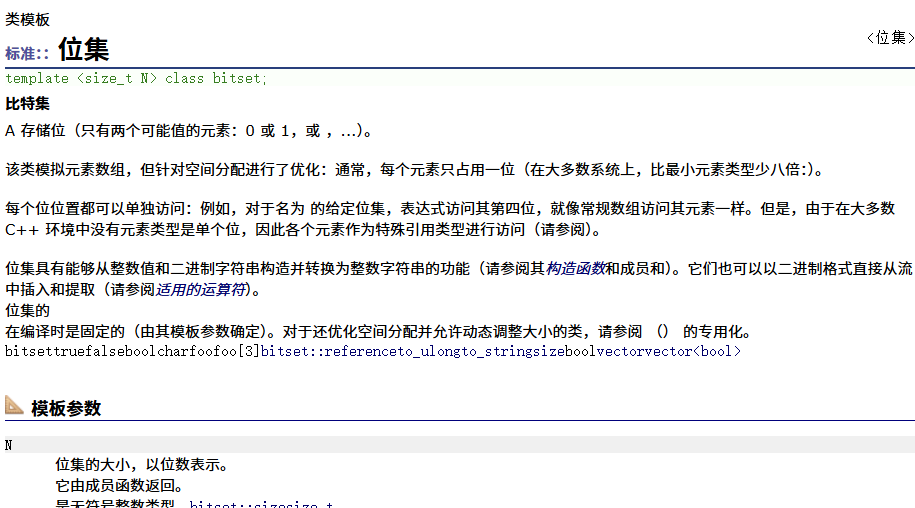
STL：bitset介绍

        官方文档：位集 - C++ 参考

        引用

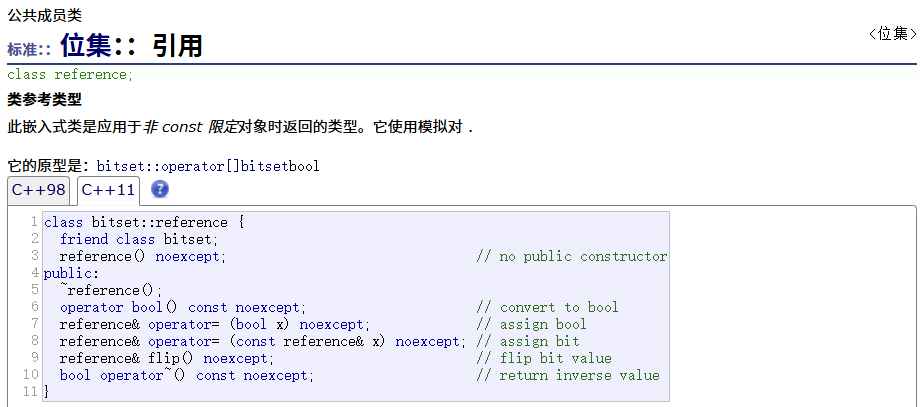
        构造函数

        

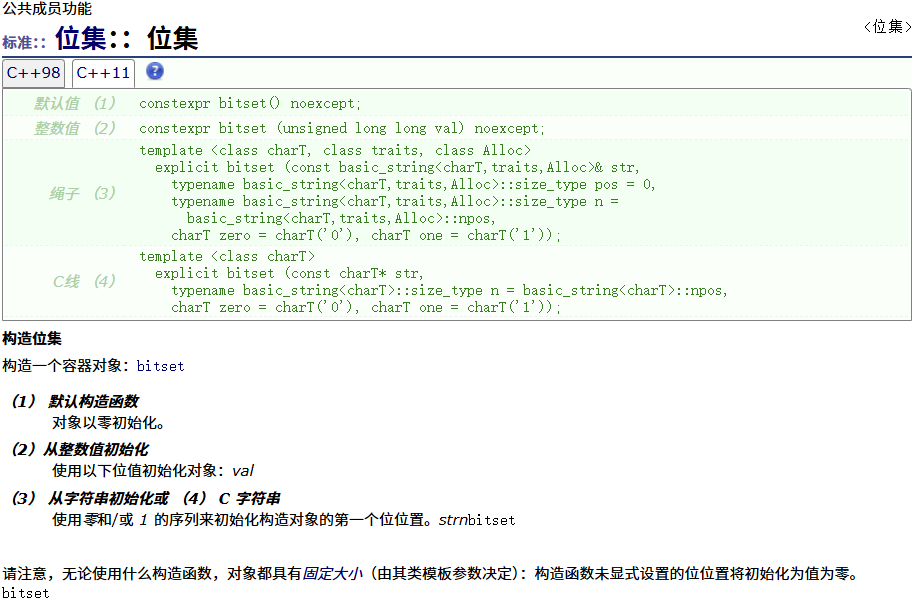
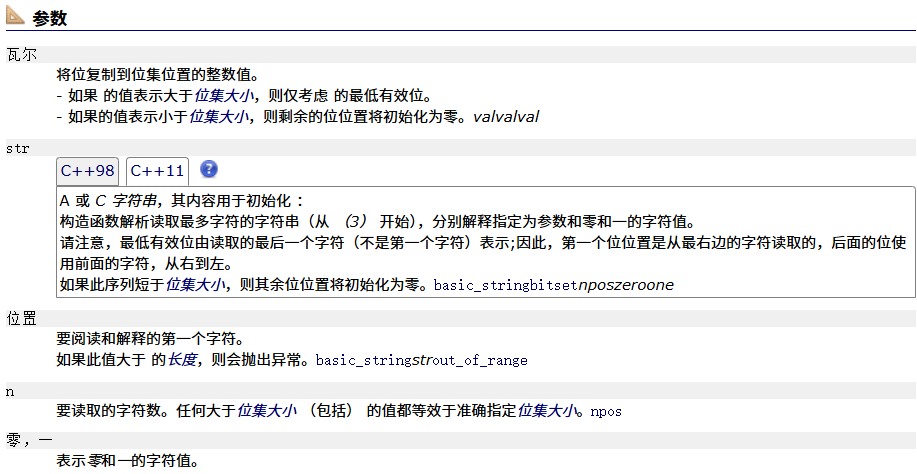
        操作符重载

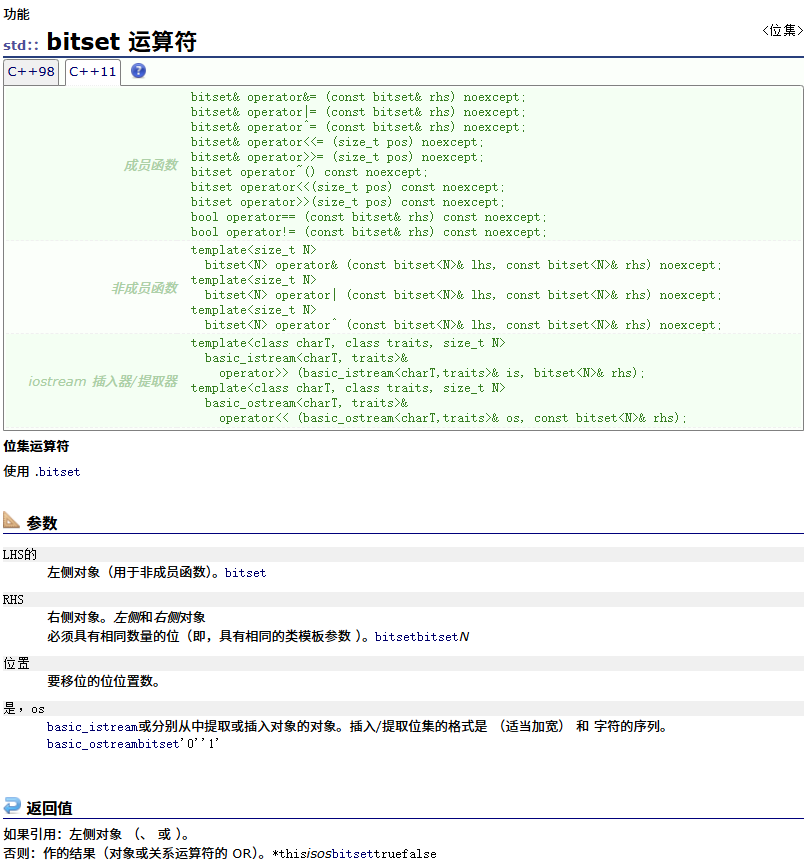
        访问

        []运算符重载

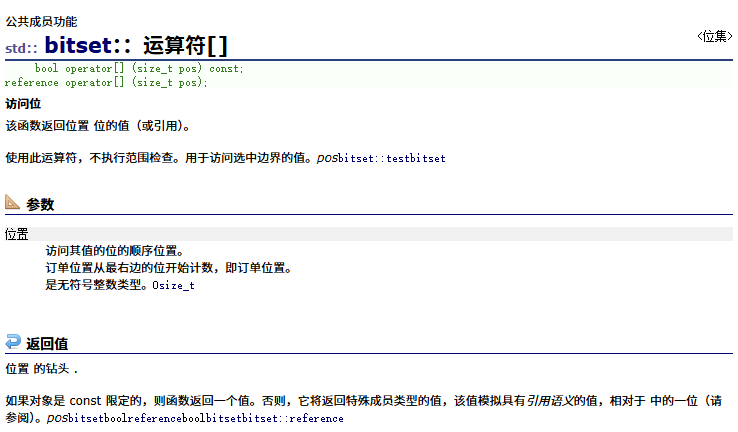
        size

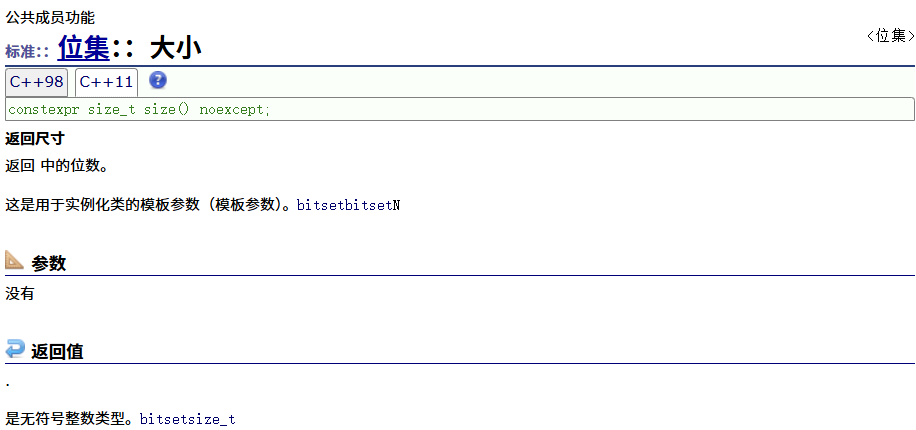
        count

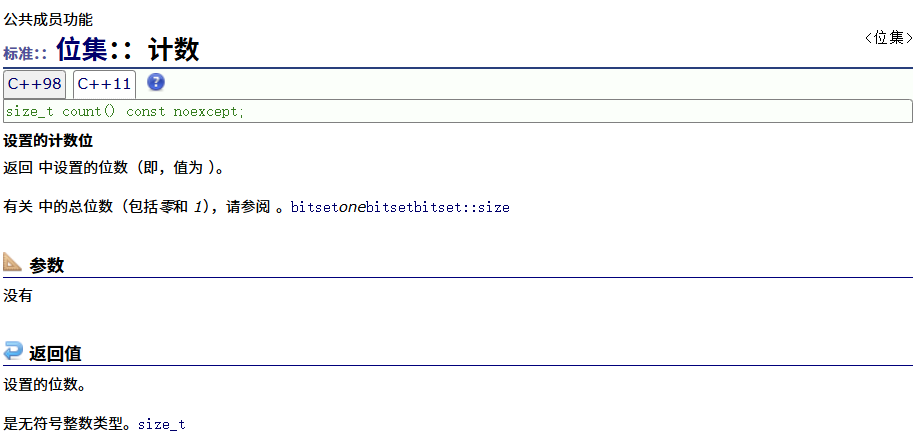
        test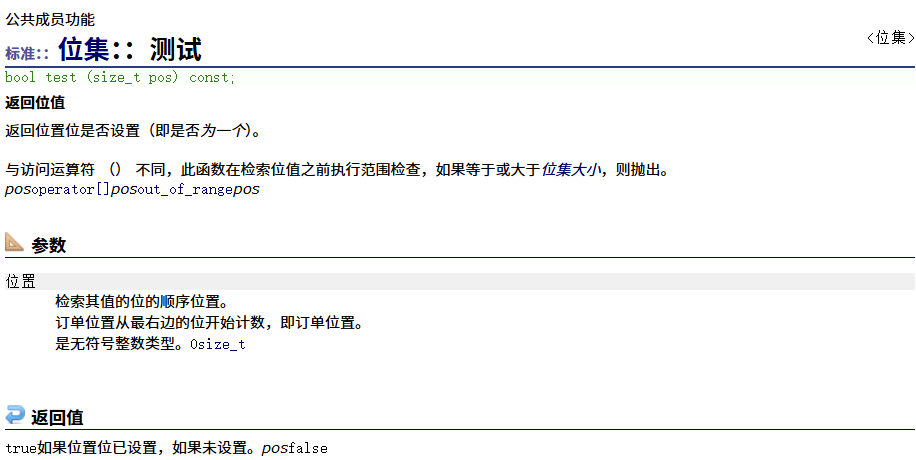  

        any

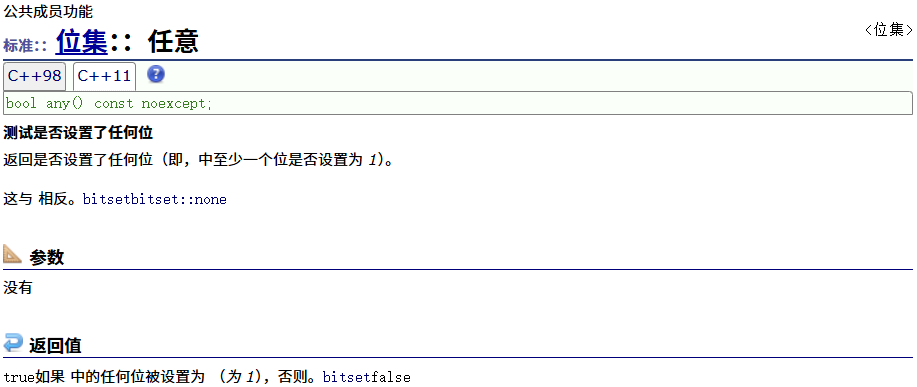
        none

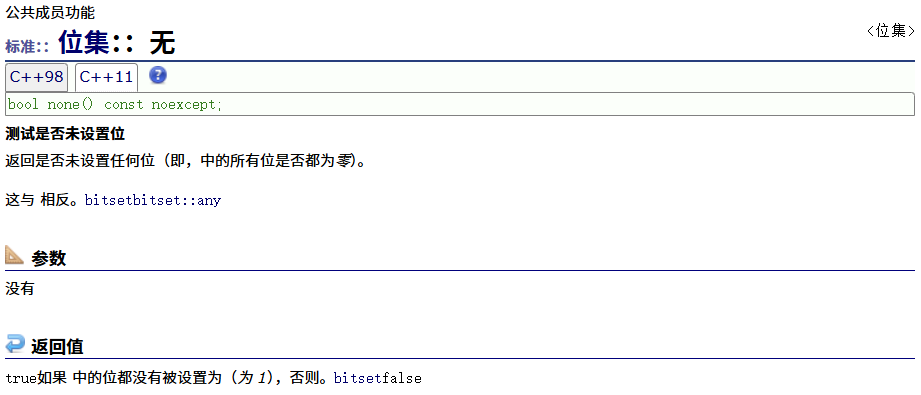
        all

        位运算

        set

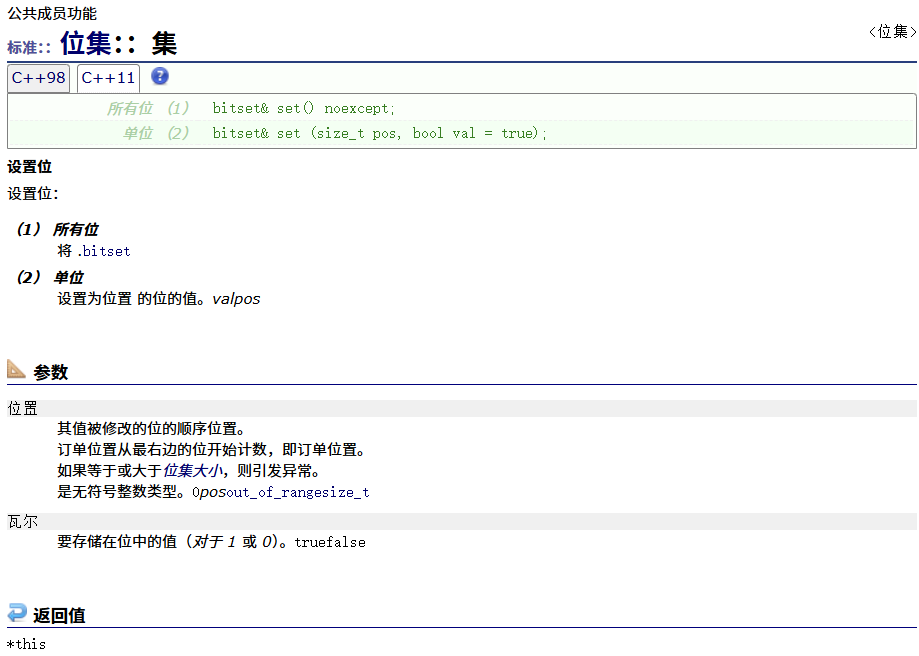
        reset

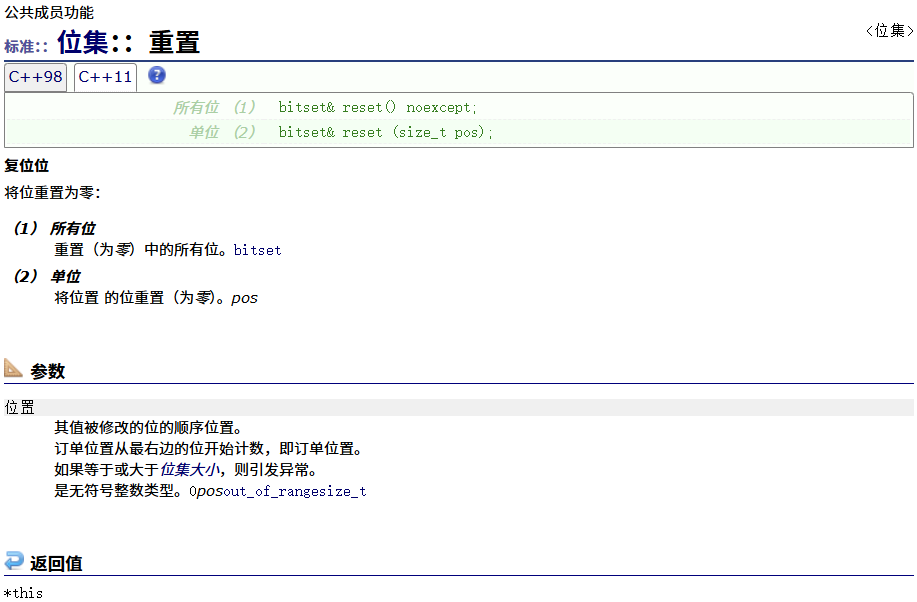
        flip

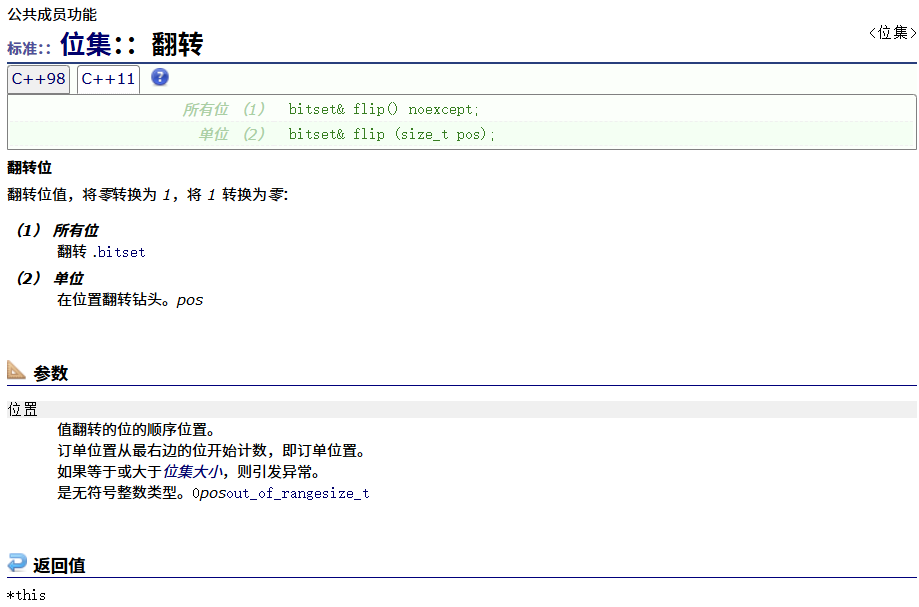
        位操作

        to_string

        to_ulong

        to_ullong

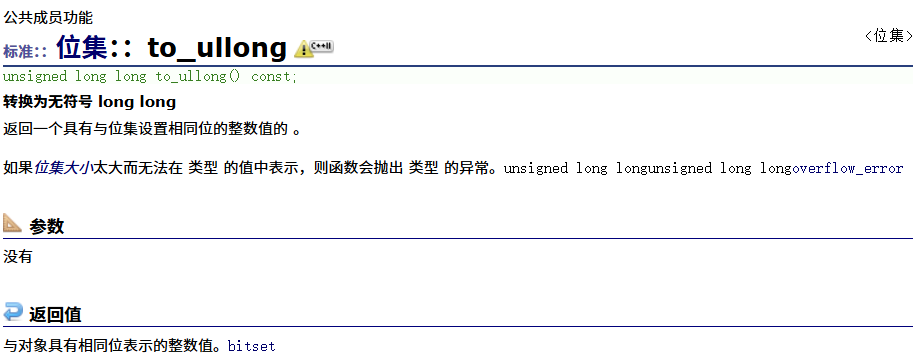
        非成员函数操作符重载

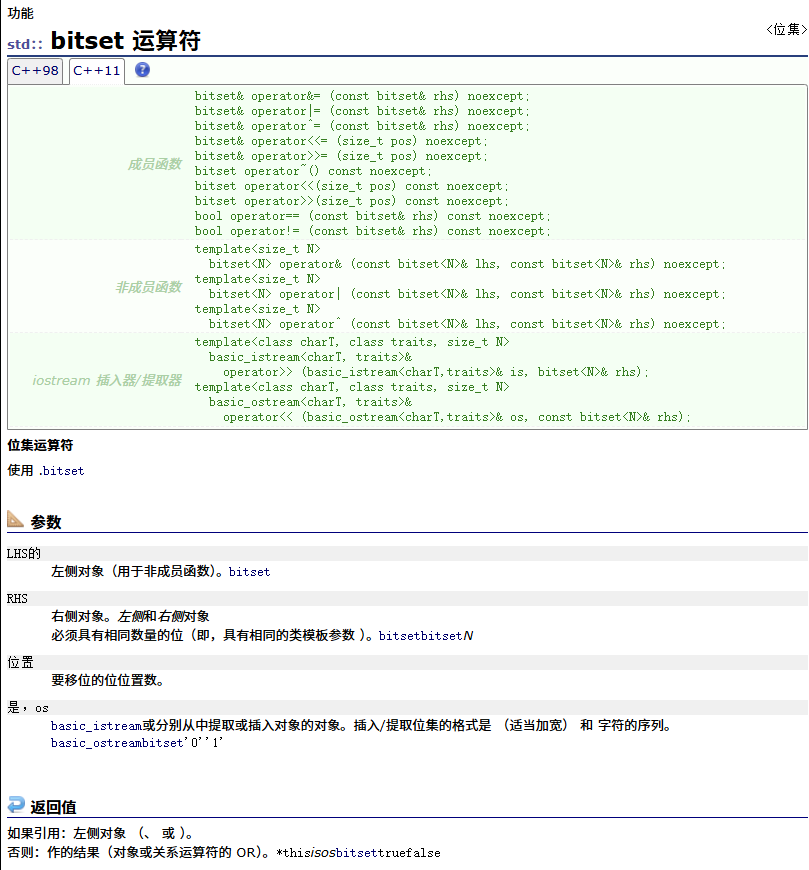
        类模板实例化

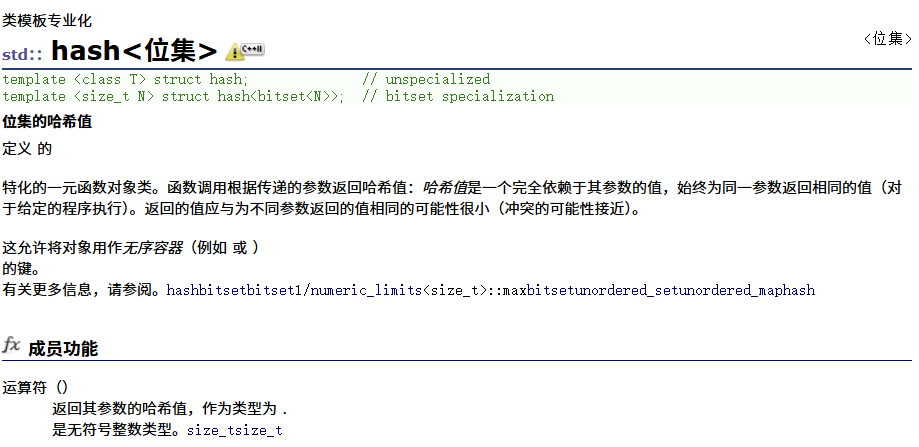
        位图的优缺点

        优点：增删查改快，节省空间

        缺点：只适⽤于整形

特性std::bitsetstd::vector<bool>
核心定义固定大小的位序列模板类std::vector 对布尔类型的特化版本
优点1. 极致性能：在栈或静态区分配，操作速度极快。
2. 接口丰富：内置大量便捷方法（all(), any(), count(), flip()等）。
3. 编译期安全：大小在编译时确定，无运行时分配失败风险。
4. 明确语义：专为位操作设计，目的明确。		1. 动态大小：可以在运行时动态调整大小（resize(), push_back()）。
2. 节省内存：与 std::bitset 一样，每个值只占1比特。
3. STL容器接口：支持迭代器（但类型是代理对象）和类似其他容器的操作（如 std::copy）。
4. 适应性强：适用于需要动态增长或缩减位集合的场景。
缺点1. 固定大小：模板参数 N 必须在编译时确定，无法运行时改变。
2. 潜在浪费：如果实际使用的位数远小于 N，会造成空间浪费。
3. 大小限制：由于在栈上分配，非常大的 N 可能导致栈溢出。		1. 不是真正容器：其迭代器不是标准随机访问迭代器，元素不是真正的 bool&，而是代理引用，可能导致模板代码出错。
2. 性能开销：动态内存分配和额外的簿记信息带来开销，操作可能慢于 std::bitset。
3. 接口陷阱：operator[] 返回的是一个代理对象，而不是 bool&，取地址会得到临时对象的地址。
4. 令人困惑：其行为与其他所有 std::vector 特化版本都不同，是标准库的一个著名“例外”
选择 std::bitset选择 std::vector<bool>
当...你需要处理的位数量是固定的、已知的（例如：状态标志集、40亿整数判存问题<1>、硬件寄存器模拟）。你需要处理的位数量在运行时是未知或可能变化的（例如：动态生成的查询结果集、可变长度的布尔过滤器）。
关键因素性能和编译期确定性是首要考虑因素。动态内存管理和灵活性是首要考虑因素

考察题目

        1、给定100亿个整数，设计算法找到只出现⼀次的整数？

        设计两个位的位图

        虽然是100亿个数，但是还是按范围开空间，所以还是开2^32个位，跟前⾯的题⽬是⼀样的

//twoBitSet.h
#pragma once
#include <vector>
#include <bitset>
namespace The_Song_of_the_end_of_the_world
{template<size_t N>class TwoBitSet{public:void set(size_t x){bool bit1 = bits2.test(x);bool bit2 = bits2.test(x);if (!bit1 && !bit2) // 00->01{bits2.set(x);}else if (!bit1 && bit2) // 01->10{bits1.set(x);bits2.reset(x);}else if (bit1 && !bit2) // 10->11{bits1.set(x);bits2.set(x);}}//返回0出现0次//返回1出现1次//返回2出现2次//返回3出现2次以上int get_count(size_t x){bool bit1 = bits1.test(x);bool bit2 = bits2.test(x);if (!bit1 && !bit2){return 0;}else if (!bit1 && bit2){return 1;}else if (bit1 && !bit2){return 2;}else{return 3;}}private:std::bitset<N> bits1;std::bitset<N> bits2; //如果用库里面的 航哥的也是不行的 这里要用自己定义的数组//才可以创建出来全ff的};
}
//test.cpp
void test_bitset2()
{The_Song_of_the_end_of_the_world::TwoBitSet<100> tbs;int a[] = { 5,7,9,2,5,99,5,5,7,5,3,9,2,55,1,5,6,6,6,6,7,9 };for (auto e : a){tbs.set(e);}for (size_t i = 0; i < 100; ++i){cout << i <<"->"<<tbs.get_count(i)<< " ";}cout<<endl;for (size_t i = 0; i < 100; ++i){//cout << i << "->" << tbs.get_count(i) << endl;if (tbs.get_count(i) == 1 || tbs.get_count(i) == 2){cout << i << " ";}}cout << endl;
}

        2、给两个⽂件，分别有100亿个整数，我们只有1G内存，如何找到两个⽂件交集？

        把数据读出来，分别放到两个位图，依次遍历，同时在两个位图的值就是交集

        3、⼀个⽂件有100亿个整数，1G内存，设计算法找到出现次数不超过2次的所有整数

布隆过滤器

        什么是布隆过滤器

        有⼀些场景下⾯，有⼤量数据需要判断是否存在，⽽这些数据不是整形，那么位图就不能使⽤了，使 ⽤红⿊树/哈希表等内存空间可能不够。这些场景就需要布隆过滤器来解决。

         布隆过滤器是由布隆（BurtonHowardBloom）在1970年提出的⼀种紧凑型的、⽐较巧妙的概率型 数据结构，特点是⾼效地插⼊和查询，可以⽤来告诉你“某样东西⼀定不存在或者可能存在”，它是 ⽤多个哈希函数，将⼀个数据映射到位图结构中。此种⽅式不仅可以提升查询效率，也可以节省⼤量 的内存空间。

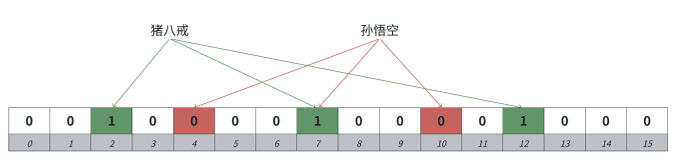
        布隆过滤器的思路就是把key先映射转成哈希整型值，再映射⼀个位，如果只映射⼀个位的话，冲突率 会⽐较多，所以可以通过多个哈希函数映射多个位，降低冲突率。

        布隆过滤器这⾥跟哈希表不⼀样，它⽆法解决哈希冲突的，因为他压根就不存储这个值，只标记映射 的位。它的思路是尽可能降低哈希冲突。判断⼀个值key在是不准确的，判断⼀个值key不在是准确 的。

布隆过滤器器误判率推导     

        说明：这个⽐较复杂，涉及概率论、极限、对数运算，求导函数等知识，有兴趣且数学功底⽐较好的推荐看，否则仅仅记住结论即可 

        推导过程：

         假设

         m：布隆过滤器的bit⻓度。

        n：插⼊过滤器的元素个数。

         k：哈希函数的个数。

        布隆过滤器哈希函数等条件下某个位设置为1的概率： 1/m

        布隆过滤器哈希函数等条件下某个位设置不为1的概率： 1− 1/m

        在经过k次哈希后，某个位置依旧不为1的概率： (1−  1/m)^ k

        

        由误判率公式可知，在k⼀定的情况下，当n增加时，误判率增加，m增加时，误判率减少。

        

        以上两篇内容可以通过以下两篇博客来深入学习了解：

        布隆过滤器（Bloom Filter）- 原理、实现和推导_布隆过滤器原理-CSDN博客

        [布隆过滤器BloomFilter] 举例说明+证明推导_bloom filter 最佳hash函数数量 推导-CSDN博客

布隆过滤器的实现

        资料：各种字符串Hash函数 - clq - 博客园

#pragma once
#include "BitSet.h"
#include <string>
namespace The_Song_of_the_end_of_the_world
{struct HashFuncBKDR{/// @detail 本算法由于在Brian Kernighan与Dennis Ritchie的《The C Programming Language》        //一书中所展示而得名，是⼀种简单快捷的hash算法，// 也是Java目前采用的的字符串的Hash算法累乘因⼦为31。size_t operator()(const string & s){size_t hash = 0;for (auto& ch : s){hash *= 31;hash += ch;}return hash;}};struct HashFuncAP{// 由Arash Partow发明的⼀种hash算法。size_t operator()(const string& s){size_t hash = 0;for (size_t i = 0; i < s.size(); i++){if ((i & 1) == 0) // 偶数位字符{hash ^= ((hash << 7) ^ (s[i]) ^ (hash >> 3));}else              // 奇数位字符{hash ^= (~((hash << 11) ^ (s[i]) ^ (hash >>5)));}}return hash;}};struct HashFuncDJB{// 由Daniel J.Bernstein教授发明的⼀种hash算法。size_t operator()(const string& s){size_t hash = 5381;for (auto& ch : s){hash = hash * 33 ^ ch;}return hash;}};//X相当于布隆过滤器的M/N//N*X为Mtemplate<size_t N,size_t X = 6,class K = std::string,class Hash1 = HashFuncBKDR,class Hash2 = HashFuncAP,class Hash3 = HashFuncDJB>class BloomFilter{public:void Set(const K& key){size_t hash1 = Hash1()(key) % M;size_t hash2 = Hash2()(key) % M;size_t hash3 = Hash3()(key) % M;_bs.set(hash1);_bs.set(hash2);_bs.set(hash3);}bool Test(const K& key){size_t hash1 = Hash1()(key) % M;if (_bs.test(hash1) == false)return false;size_t hash2 = Hash2()(key) % M;if (_bs.test(hash2) == false)return false;size_t hash3 = Hash3()(key) % M;if (_bs.test(hash3) == false)return false;return true;}// 获取公式计算出的误判率        double getFalseProbability(){double p = pow((1.0 - pow(2.71, -3.0 / X)), 3.0);return p;}private:static const size_t M = X * N;//我们实现位图是⽤vector,也就是堆上开的空间The_Song_of_the_end_of_the_world::BitSet<M> _bs;//std::bitset<M> _bs;// vs下std的位图是开的静态数组，	M太⼤会存在崩的问题        // // 解决⽅案就是bitset	对象整体new⼀下，空间就开到堆上了        // //std::bitset<M>* _bs = new std::bitset<M>;};
}

布隆过滤器删除问题

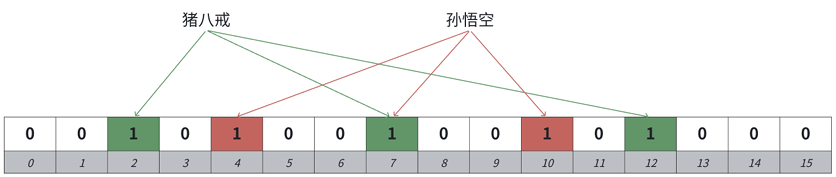
        布隆过滤器默认是不⽀持删除的，因为⽐如"猪⼋戒“和”孙悟空“都映射在布隆过滤器中，他们映射 的位有⼀个位是共同映射的(冲突的)，如果我们把孙悟空删掉，那么再去查找“猪⼋戒”会查找不到， 因为那么“猪⼋戒”间接被删掉了。

        解决⽅案：可以考虑计数标记的⽅式，⼀个位置⽤多个位标记，记录映射这个位的计数值，删除时， 仅仅减减计数，那么就可以某种程度⽀持删除。

        但是这个⽅案也有缺陷，如果⼀个值不在布隆过滤器 中，我们去删除，减减了映射位的计数，那么会影响已存在的值，也就是说，⼀个确定存在的值，可能会变成不存在。

        当然也有⼈提出，我们可以考虑计数⽅式⽀持删除，但是定期重建⼀ 下布隆过滤器，这也是⼀种思路。

布隆过滤器的优缺点

        ⾸先我们分析⼀下布隆过滤器的优缺点：

        优点：效率⾼，节省空间，相⽐位图，可以适⽤于各种类型的标记过滤

        缺点：存在误判(在是不准确的，不在是准确的)，不好⽀持删除

优点缺点
空间效率极高存在误判率（假阳性）
相比其他数据结构（如哈希表），布隆过滤器使用位数组表示集合，空间占用极小。例如，存储10亿个元素只需约1.2GB内存（误判率1%）。布隆过滤器可能会错误地判断某个不存在的元素为存在（假阳性），但不会错误判断存在的元素为不存在（真阴性）。
查询时间恒定无法删除元素
判断元素是否存在的时间复杂度是O(k)，其中k是哈希函数数量，与数据量大小无关。标准的布隆过滤器不支持删除操作，因为多个元素可能共享同一位。删除一个元素会影响其他元素的判断。
并行处理能力强无法获取实际存储的元素
多个布隆过滤器可以通过位或操作进行合并，非常适合分布式系统。布隆过滤器只存储元素的存在信息，无法检索或遍历实际存储的元素。
内存访问模式友好需要预先确定容量
所有操作都是对位数组的随机访问，缓存友好，性能高。布隆过滤器的容量和误判率需要在创建时确定，后期难以调整。
保密性较好哈希函数选择影响性能
布隆过滤器不存储原始数据，只存储哈希结果，一定程度上保护了数据隐私。哈希函数的选择和质量直接影响布隆过滤器的性能和误判率。
支持大规模数据不适用于低误判率要求的场景
可以处理海量数据的成员存在性检查，远超内存容量的数据也可以处理。对于要求100%准确性的场景，布隆过滤器不适用

布隆过滤器的应用

        爬⾍系统中URL去重： 在爬⾍系统中，为了避免重复爬取相同的URL，可以使⽤布隆过滤器来进⾏URL去重。爬取到的URL可 以通过布隆过滤器进⾏判断，已经存在的URL则可以直接忽略，避免重复的⽹络请求和数据处理。

        垃圾邮件过滤： 在垃圾邮件过滤系统中，布隆过滤器可以⽤来判断邮件是否是垃圾邮件。系统可以将已知的垃圾邮件 的特征信息存储在布隆过滤器中，当新的邮件到达时，可以通过布隆过滤器快速判断是否为垃圾邮 件，从⽽提⾼过滤的效率。

        预防缓存穿透 ：在分布式缓存系统中，布隆过滤器可以⽤来解决缓存穿透的问题。缓存穿透是指恶意⽤⼾请求⼀个不 存在的数据，导致请求直接访问数据库，造成数据库压⼒过⼤。布隆过滤器可以先判断请求的数据是 否存在于布隆过滤器中，如果不存在，直接返回不存在，避免对数据库的⽆效查询。

        对数据库查询提效 ：在数据库中，布隆过滤器可以⽤来加速查询操作。例如：⼀个app要快速判断⼀个电话号码是否注册 过，可以使⽤布隆过滤器来判断⼀个⽤⼾电话号码是否存在于表中，如果不存在，可以直接返回不存 在，避免对数据库进⾏⽆⽤的查询操作。如果在，再去数据库查询进⾏⼆次确认。

应用领域具体应用关键作用
数据库系统BigTable, HBase, Cassandra减少磁盘I/O：快速判断某个键是否肯定不存在于某个 SSTable 或数据块中，避免无效的磁盘扫描。
缓存系统Redis, Memcached, 网站缓存防止缓存穿透：在查询缓存和数据库前，先检查布隆过滤器。若键不存在，则直接返回，避免恶意请求冲击后端数据库。
网络与安全网络爬虫, 恶意网址/邮件过滤, Chrome 浏览器高效去重与过滤：用于海量URL去重；快速判断网址/邮件特征是否在黑名单中，误判的“假阳性”结果通常是可接受的。
分布式系统分布式缓存, 数据同步快速协同：在分布式节点间快速判断数据是否可能存在于其他节点，减少不必要的网络通信。
大数据处理MapReduce, 流数据处理数据预过滤：在Map阶段或流处理中过滤掉已经处理过的数据，显著降低数据传输和计算开销。
区块链比特币/以太坊轻钱包 (SPV节点)交易过滤：轻节点创建布隆过滤器并发送给全节点，全节点只返回可能相关的交易，极大减少数据传输量。

海量信息处理问题        

        10亿个整数里面最大的前100个。

        经典topk问题，⽤堆解决

        位图相关的面试题

        给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。（本题为腾讯/百度等公司出过的一个面试题）

        解题思路1：暴力遍历，时间复杂度O(N)O(N)，太慢

        解题思路2：排序+二分查找。时间复杂度消耗 O(N∗log⁡N)+O(log⁡N)O(N∗logN)+O(logN)

        深入分析：解题思路2是否可行，我们先算算40亿个数据大概需要多少内存。

        1G=1024MB=1024∗1024KB=1024∗1024∗1024Byte

        那么40亿个数据内存是16G，显然是不可行的，只能存储到磁盘文件里，而二分查找只针对内存中的有序数组进行查找。

        解题思路3: 数据是否在给定的整形数据中，结果是在或者不在，刚好是两种状态，那么可以使用一个二进制比特位来代表数据是否存在的信息，如果二进制比特位为1，代表存在，为0代表不存在。那么我们设计一个用位表示数据是否存在的数据结构，这个数据结构就叫位图。

        给两个文件，分别有100亿个query（查询），我们只有1G内存，如何找到两个文件交 集？

        分析：假设平均每个query字符串50byte，100亿个query就是5000亿byte，约等于500G(1G约等于 10亿多Byte) 哈希表/红⿊树等数据结构肯定是⽆能为⼒的。

         解决⽅案1：这个⾸先可以⽤布隆过滤器解决，⼀个⽂件中的query放进布隆过滤器，另⼀个⽂件依次 查找，在的就是交集，问题就是找到交集不够准确，因为在的值可能是误判的，但是交集⼀定被找到 了。

         解决⽅案2：

        哈希切分，⾸先内存的访问速度远⼤于硬盘，⼤⽂件放到内存搞不定，那么我们可以考虑切分为⼩ ⽂件，再放进内存处理。

        但是不要平均切分，因为平均切分以后，每个⼩⽂件都需要依次暴⼒处理，效率还是太低了。

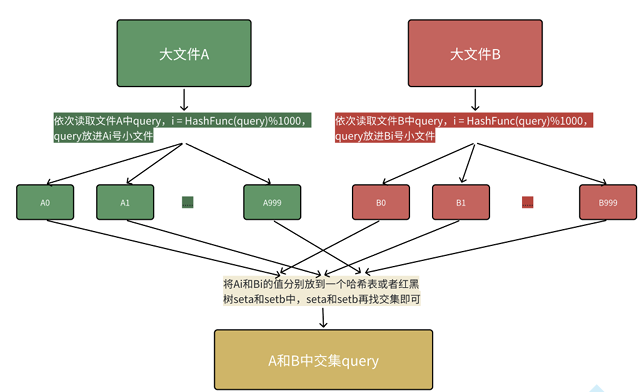
        可以利⽤哈希切分，依次读取⽂件中query，i=HashFunc(query)%N，N为准备切分多少分⼩⽂ 件，N取决于切成多少份，内存能放下，query放进第i号⼩⽂件，这样A和B中相同的query算出的 hash值i是⼀样的，相同的query就进⼊的编号相同的⼩⽂件就可以编号相同的⽂件直接找交集，不 ⽤交叉找，效率就提升了。

        本质是相同的query在哈希切分过程中，⼀定进⼊的同⼀个⼩⽂件Ai和Bi，不可能出现A中的的 query进⼊Ai，但是B中的相同query进⼊了和Bj的情况，所以对Ai和Bi进⾏求交集即可，不需要Ai 和Bj求交集。（本段表述中i和j是不同的整数）

        哈希切分的问题就是每个⼩⽂件不是均匀切分的，可能会导致某个⼩⽂件很⼤内存放不下。我们细 细分析⼀下某个⼩⽂件很⼤有两种情况：

        1.这个⼩⽂件中⼤部分是同⼀个query。

        2.这个⼩⽂件是 有很多的不同query构成，本质是这些query冲突了。

        针对情况1，其实放到内存的set中是可以放 下的，因为set是去重的。

        针对情况2，需要换个哈希函数继续⼆次哈希切分。所以本体我们遇到⼤ 于1G⼩⽂件，可以继续读到set中找交集，若setinsert时抛出了异常(set插⼊数据抛异常只可能是 申请内存失败了，不会有其他情况)，那么就说明内存放不下是情况2，换个哈希函数进⾏⼆次哈希 切分后再对应找交集

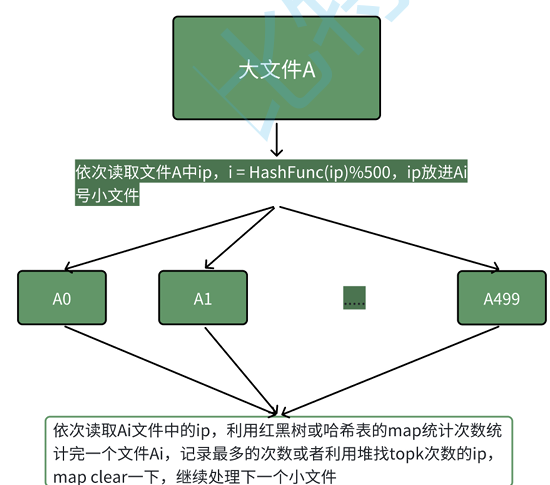
        给⼀个超过100G⼤⼩的logfile,log中存着ip地址,设计算法找到出现次数最 多的ip地址？查找出现次数前10的ip地址

        本题的思路跟上题完全类似，依次读取⽂件A中query，i=HashFunc(query)%500，query放进Ai号⼩ ⽂件，然后依次⽤map对每个Ai⼩⽂件统计ip次数，同时求出现次数最多的ip或者topk ip。本质是相同的ip在哈希切分过程中，⼀定进⼊的同⼀个⼩⽂件Ai，不可能出现同⼀个ip进⼊Ai和Aj 的情况，所以对Ai进⾏统计次数就是准确的ip次数。

        本期关于哈希表和哈希算法的进阶应用到这里就结束了，喜欢请点个赞谢谢

封面图自取：

http://www.dtcms.com/a/392814.html

相关文章：

  • 林曦词典｜无痛学习法
  • 树莓派CM4显示测序合集
  • python创建虚拟环境相关命令
  • 如何用AI把博客文章，“洗”成一篇学术论文？
  • 应用密码学课程复习汇总2——古典密码学
  • 应用密码学课程复习汇总1——课程导入
  • PyTorch 中 AlexNet 的构建与核心技术解析
  • 一文读懂：三防手机的定义、特性与使用场景
  • EG800G-CN不联网不定位
  • sqzb_alldsd——板子
  • Windows 快速检测 Docker / WSL2 安装环境脚本（附 GUI 版本）
  • Redis最佳实践——电商应用的性能监控与告警体系设计详解
  • 【C++】C++11（二）
  • 如何解决 pip install 安装报错 ModuleNotFoundError: No module named ‘selenium’ 问题
  • 实测美团LongCat-Flash：当大模型装上“速度引擎”，能否改写智能体战局？
  • unicode ascii utf-8的区别
  • Rust_2025：阶段1：day6.1 collect补充 ,迭代器补充 ，闭包，Hashmap搜索指定值的个数，合并迭代器
  • ESP32- 项目应用2 音乐播放器之音响驱动 #2
  • Datawhale25年9月组队学习：llm-preview+Task2：大模型使用
  • Agent记忆：Memvid、Memary、MemoryOS
  • 《主流PLC品牌型号大全解析》，电气设计时PLC应该怎么选
  • 从92到102，一建实务突破之路：坚持与自我超越
  • 探索C语言中字符串长度的计算方法
  • 使用node框架 Express开发仓库管理系统练习项目
  • 网络系统管理
  • 【Vue3 ✨】Vue3 入门之旅 · 第四篇：组件的创建与传递数据
  • PHP魔法函数和超全局数组介绍——第一阶段
  • 深入剖析“惊群效应”：从Java的notifyAll到epoll的解决方案
  • 鸿蒙应用统一埋点体系设计
  • Rust_2025：阶段1：day6.2 Box ，Cow ，Rc ，Refcell ，Arc，线程(join（），lock（），子线程与主线程通信