【C++】STL详解（九）—priority_queue的使用与模拟实现

✨ 坚持用 清晰易懂的图解 + 代码语言， 让每个知识点都 简单直观 ！
🚀 个人主页 ：不呆头 · CSDN
🌱 代码仓库 ：不呆头 · Gitee
📌 专栏系列 ：

• 📖 《C语言》
• 🧩 《数据结构》
• 💡 《C++》
• 🐧 《Linux》

💬 座右铭 ： “不患无位，患所以立。”

---

---

摘要

priority_queue 是 C++ STL 中的重要容器适配器，它通过堆结构维护元素的优先级，使得每次访问和删除的都是当前优先级最高的元素。本文从 priority_queue 的定义方式与常用接口出发，结合示例代码展示其基本用法，并进一步通过模拟实现深入剖析了堆的向上调整与向下调整算法，帮助读者从底层原理的角度全面理解 priority_queue 的运行机制。无论是日常刷题，还是在工程中处理调度、路径搜索等场景，掌握 priority_queue 都能大幅提升代码效率与思路清晰度。

📌 编程箴言：
“好的C++代码就像好酒，需要时间沉淀。”

---

目录

一、priority_queue的认识

priority_queue 是 C++ STL 提供的一种容器适配器，本质上依赖底层容器（默认是 vector）来存储数据，并通过堆的方式来维护元素顺序，它和普通队列不同，不是“先来先走”，而是按照优先级大小决定谁先出来；其中第一个模板参数（class T） 表示存储的数据类型，第二个模板参数（class Container = vector） 决定底层用什么容器，第三个参数则定义比较规则 默认是大顶堆，即数值大的优先级高，也可以改成小顶堆）；因此，它最大的特点就是无论插入多少元素，每次取出的都是当前优先级最高的那个，非常适合用在需要频繁获取极值的场景，比如贪心算法、最短路径、任务调度等，你可以把它想象成一个“VIP 排队窗口”，永远让最重要的人排在最前面。

---

二、priority_queue的使用

1. 定义方式

1.1 大堆

储存数据类型为int，容器为vector，构造大堆。

priority_queue<int, vector<int>, less<int>> q1;

---

1.2 小堆

储存数据类型为int，容器为vector，构造小堆。

priority_queue<int, vector<int>, greater<int>> q2;

---

1.3 不指定

不指定数据类型，容器，和内部需要构造的堆。

priority_queue<int> q;

注意： 此时默认使用vector底层容器，内部默认为大堆。

---

2. priority_queue各个接口的使用

2.1 表格

接口	作用	说明
empty()	判断队列是否为空	为空返回 true，否则返回 false
size()	返回队列中元素个数	常用于统计当前优先级队列的规模
top()	访问队头元素	获取优先级最高的元素（但不删除），复杂度 O(1)
push(x)	插入元素 x	会自动调整堆结构，复杂度 O(log n)
pop()	删除队头元素	移除当前优先级最高的元素，复杂度 O(log n)
swap(q)	交换两个队列的内容	与另一个优先级队列整体交换数据

---

2.2 示例

#include <iostream>
#include <functional>
#include <queue>
using namespace std;
int main()
{priority_queue<int> q;q.push(5);q.push(2);q.push(0);q.push(1);q.push(3);q.push(1);q.push(4);while (!q.empty()){cout << q.top() << " ";q.pop();}cout << endl; //5 4 3 2 1 1 0return 0;
}

---

三、priority_queue的模拟实现

以下堆的调整算法均以大堆为例

1. 堆的向上调整算法

大堆为例，堆的向上调整算法就是在大堆的末尾插入一个数据后，经过一系列的调整，使其仍然是一个大堆。

主要思路：

1. 将我们想要插入的数据和它的父节点进行比较，如果大于其父节点就和父节点交换，以此类推，直到插入的数据比其父节点小则停止交换；
2. 和父节点交换后我们需要将父节点的下标赋值给需要插入的数据，然后重新计算这个插入数据的父节点。

---

我们想在大堆的末尾插入一个新的数据：96

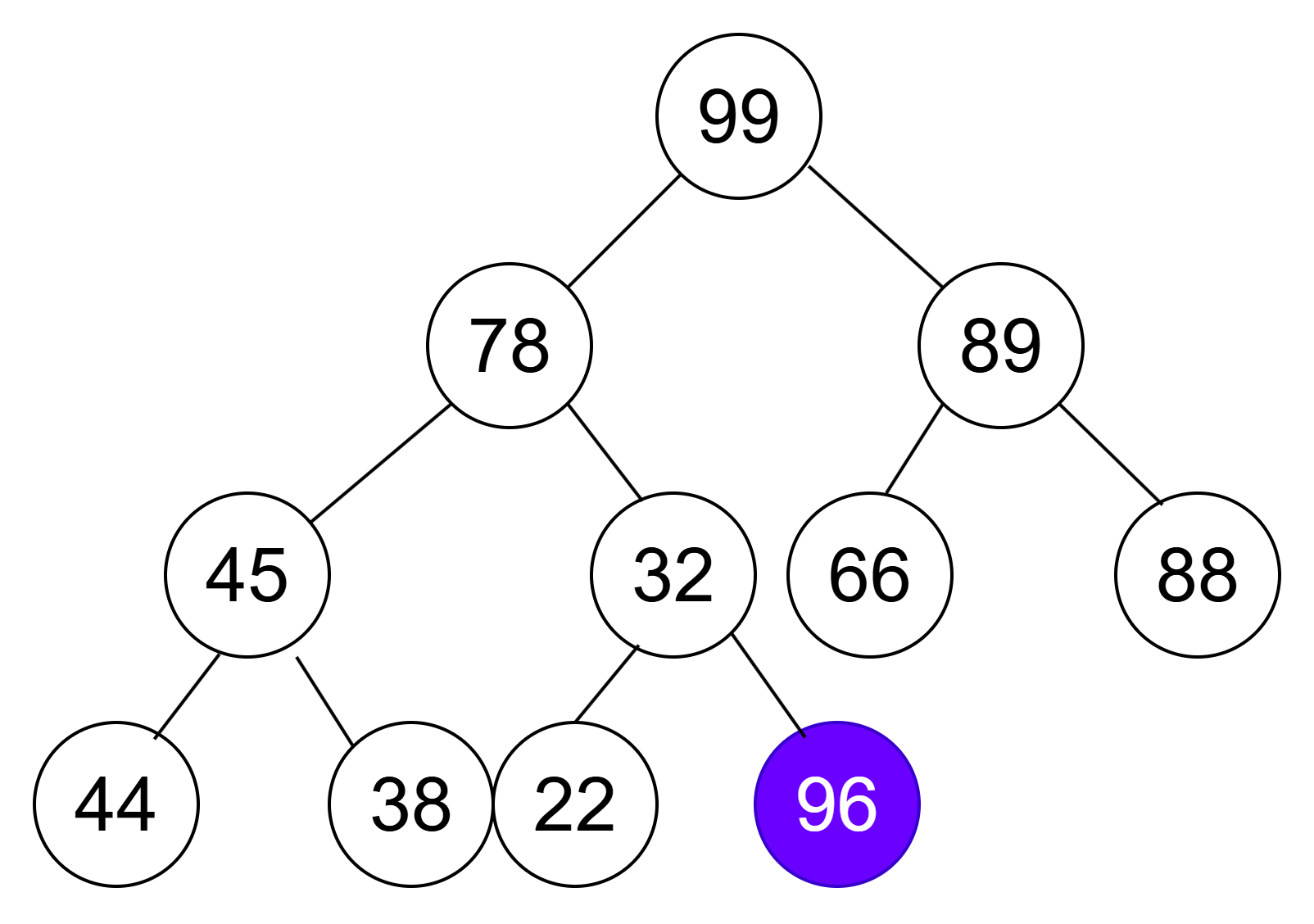
经过我们的调整应该为：

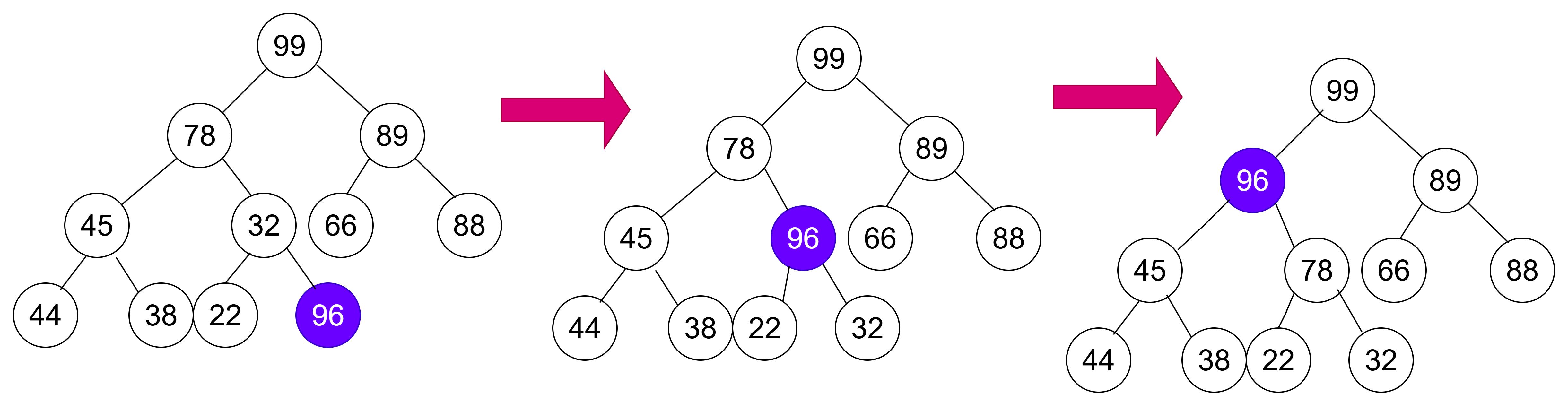
    void adjust_up(int child){int parent = (child - 1) / 2; //求父节点while(child > 0) //只要没到根节点，继续调整{if (_con[parent] < _con[child])//父节点小于子节点{swap(_con[parent], _con[child]);//交换child = parent;//将父节点作为新的子节点，继续往上比较parent = (child - 1) / 2;//更新父节点}else{break;}}}

---

2. 堆的向下调整算法

以大堆为例，使用堆的向下调整算法有一个前提，就是待向下调整的结点的左子树和右子树必须都为大堆。

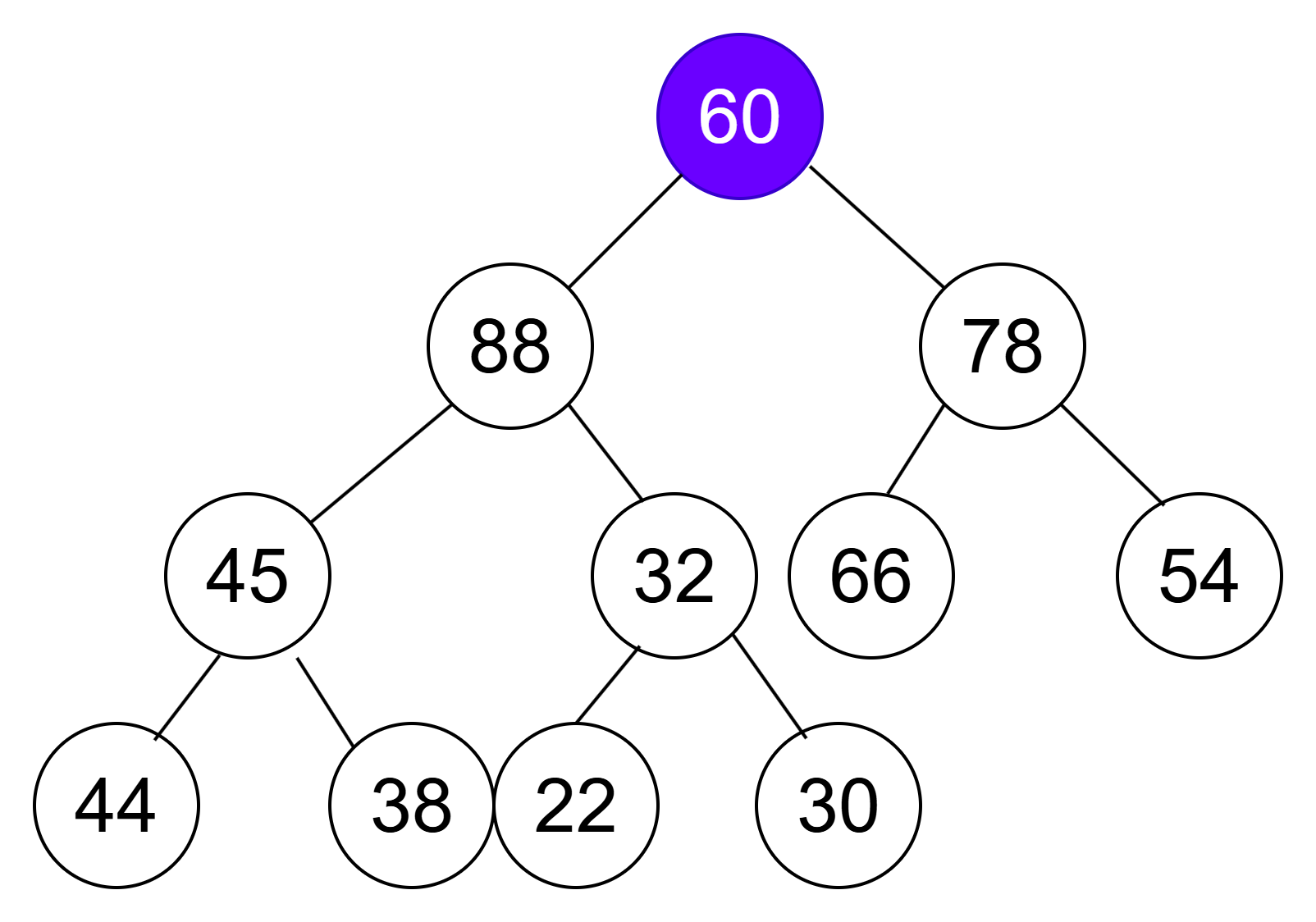
主要思路：

1. 将目标结点与其较大的子结点进行比较。
2. 若目标结点的值比其较大的子结点的值小，则交换目标结点与其较大的子结点的位置，并将原目标结点的较大子结点当作新的目标结点继续进行向下调整；若目标结点的值比其较大子结点的值大，则停止向下调整，此时该树已经是大堆了。

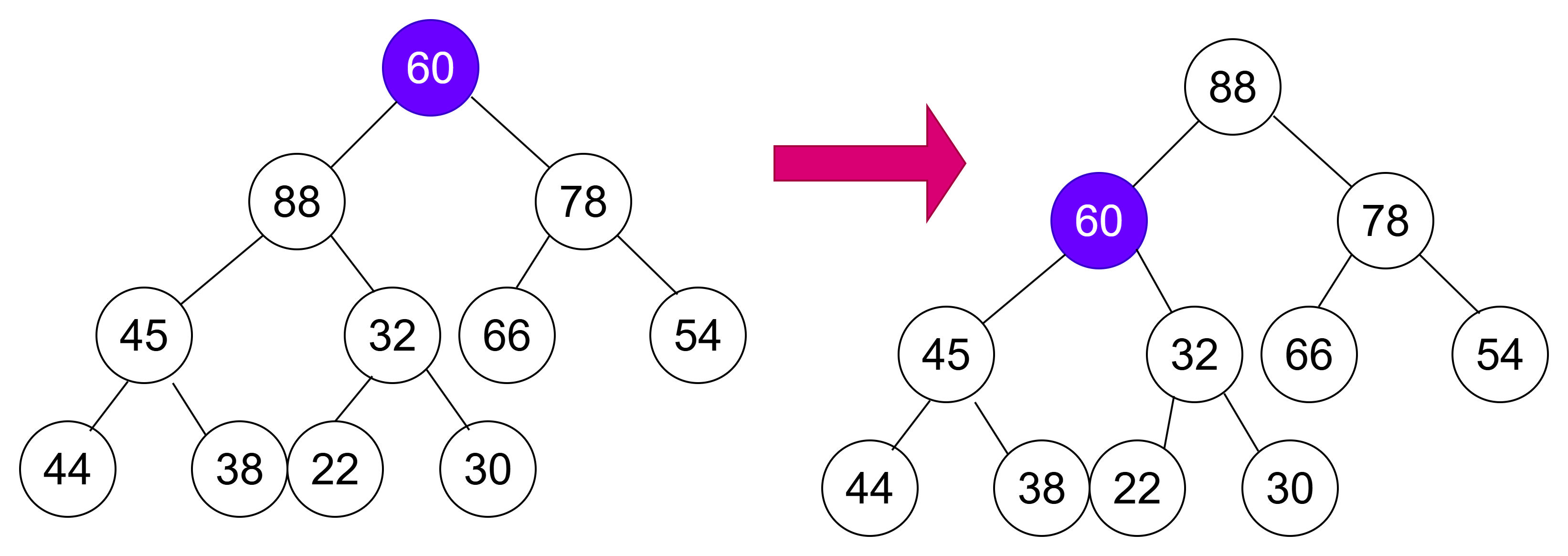
// 大顶堆的向下调整
void adjust_down(int parent)
{// 先找到 parent 的左孩子下标int child = parent * 2 + 1; // 左孩子 = 2*parent + 1// 只要 child 没越界，就继续比较while (child < _con.size()){// 如果右孩子存在，并且右孩子比左孩子大，// 那么让 child 指向右孩子（因为要和更大的孩子比较）if (child + 1 < _con.size() && _con[child] < _con[child + 1]){child++;}// 如果父节点比孩子小，就交换if (_con[parent] < _con[child]){swap(_con[parent], _con[child]);}else{// 父节点已经比孩子大了，说明局部已经是大顶堆，结束循环break;}// 交换后，继续向下调整parent = child;          // 更新父节点下标child = parent * 2 + 1;  // 重新计算左孩子下标}
}

3. 模拟实现

3.1 常用的接口

接口	功能说明
priority_queue()	构造一个空的优先级队列（默认大顶堆）
priority_queue(InputIterator first, InputIterator last)	用迭代器区间构造优先级队列
push(const T& val)	向堆中插入一个元素，并保持堆结构
pop()	删除堆顶元素（不会返回值）
top()	返回堆顶元素（最大值或最小值，取决于比较器）
empty()	判断优先级队列是否为空
size()	返回队列中元素的个数

3.2 构造函数

1. 无参构造：直接构造一个空的优先级队列，默认情况下其内部维护的是一个大根堆。
2. 迭代器区间构造：利用 [begin, end) 区间内的元素来构造优先级队列。该区间是一个左闭右开的结构，即包含 begin 指向的元素但不包含 end。构造过程中，会先通过迭代器解引用，将区间内的数据依次尾插到底层容器 _con 中，直到首尾迭代器相等时结束插入。完成数据存储后，还需要调用 向下调整算法（Heapify），从最后一个非叶子结点开始依次向下调整，最终使 _con 满足大根堆的性质。这样整个构造过程既完成了数据的批量插入，又确保了优先级队列的堆结构正确性。

// 迭代器区间构造函数 —— 使用一段迭代器区间来初始化 priority_queue
template<typename InputIterator>
priority_queue(InputIterator begin, InputIterator end)
{// 1. 将 [begin, end) 区间内的所有元素依次插入到底层容器 _con 中while (begin != end){_con.push_back(*begin);  // 将迭代器指向的元素尾插到 _con 中++begin;                 // 迭代器后移}// 2. 使用向下调整（建堆）的方式，将无序的 _con 调整为大堆结构// 从最后一个非叶子结点开始，依次向下调整，直到根节点for (int i = (_con.size() - 1 - 1) / 2; i >= 0; i--){adjust_down(i);  // 将以 i 为根的子树调整为符合大堆性质}// 至此，_con 已经满足大堆结构，也就完成了 priority_queue 的初始化
}

至于无参构造，虽然无参构造函数本身不需要做任何额外操作，但它必须显式定义。原因在于：当类中显式定义了其他构造函数（如迭代器区间构造函数）后，编译器将不会再自动生成默认构造函数。如果此时用户尝试通过无参方式构造 priority_queue，就会因为找不到匹配的构造函数而导致编译错误。因此，需要手动提供一个“空实现”的无参构造函数，以确保接口完整性。

另外，类中的成员变量 _con（类型为 vector<T>）的构造和析构操作无需我们手动处理，vector 作为标准库容器会自动完成资源管理。因此，我们只需显式声明无参构造函数，而 _con 的生命周期由其自身负责管理。

// 无参构造函数
priority_queue()
{// 什么都不需要做// 因为成员变量 _con 是一个 vector<T> 对象，// 它会在构造 priority_queue 时自动调用 vector 的默认构造函数，// 完成底层存储空间的初始化。// // 我们显式写出这个无参构造函数的原因是：// 当类中已经显式定义了其他构造函数（比如迭代器区间构造函数），// 编译器将不会再自动生成默认构造函数。// 如果用户需要通过无参方式构造 priority_queue，// 而我们没有显式写出该构造函数，就会导致编译错误。
}

---

4. push

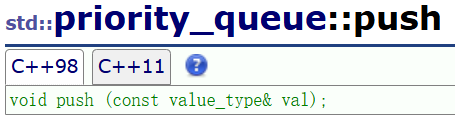
因为我们不知道这里的储存数据类型是自定义类型还是内置类型，所以我们采用引用传参（避免自定义类型传参引发的消耗太大），并且我们不对插入的数据进行修改，所以加一个const修改；push是实行尾插操作，直接调用push_back就行，并且使用向上调整算法，自动构建成一个大堆。

void push(const T& val)
{_con.push_back(val);adjust_up(_con.size() - 1);
}

---

5. pop

pop是对首个数据的删除，即priority_queue优先级队列结构的堆顶数据，这时候我们首元素和尾元素进行交换，此时原来的首元素在尾元素的位置上，我们直接执行一次尾删的操作，然后原来的尾元素在堆顶位置可能会破坏大堆的结构，我们在执行一下向下调整算法。

void pop()
{swap(_con[0], _con[_con.size() - 1]);_con.pop_back();adjust_down(0);
}

---

6. top

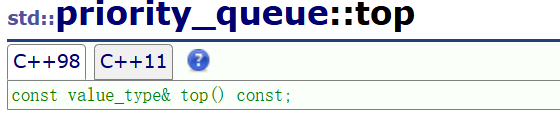
top 用于获取 priority_queue 优先级队列的堆顶元素的引用（即最大值所在位置）。在底层实现中，堆顶元素存储在容器 _con 的首位置（下标 0），因此直接返回 _con[0] 即可。

1. top 返回的是 const 引用，这保证了用户只能读取堆顶的值，而不能直接修改它，从而避免破坏堆的有序性。
2. 接口需要声明为 const 成员函数，这样即使 priority_queue 对象是常量，也可以安全调用 top 来访问堆顶元素。

const T& top() const
{return _con[0]; // 堆顶元素始终在数组的首位置
}

---

7. empty

bool empty() const
{return _con.empty();
}

8. size

👌你的总结已经很到位了，我帮你稍微整理一下，使其更专业、简洁：

---

size 用于获取 priority_queue 优先级队列中当前存储的数据个数。
其实现直接调用底层容器 _con.size() 即可。

1. size 仅仅是一个 只读操作，不会修改容器数据，因此必须在函数后加上 const，以保证常量对象也能调用。
2. 返回值类型应选择 size_t，它是无符号整型，能够正确表达元素数量（断然不会为负数）。

size_t size() const
{return _con.size(); // 返回底层容器元素个数
}

---

四、测试

1. .h文件

#pragma once
#include <vector>
#include <iostream>namespace dh
{template<typename T, typename Container = std::vector<T>>class priority_queue{private:// 向下调整函数：保证以 parent 为根的子树符合大堆性质void adjust_down(int parent){int child = parent * 2 + 1; // 左孩子下标while (child < _con.size()){// 如果右孩子存在，并且右孩子更大，让 child 指向右孩子if (child + 1 < _con.size() && _con[child] < _con[child + 1]){child++;}// 如果父节点比孩子小，交换if (_con[parent] < _con[child]){std::swap(_con[parent], _con[child]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{// 已经符合大堆性质，退出循环break;}}}// 向上调整函数：新元素插入后，从下往上调整void adjust_up(int child){int parent = (child - 1) / 2; // 父节点下标while (child > 0){if (_con[parent] < _con[child]) // 父节点比子节点小{std::swap(_con[parent], _con[child]);// 更新下标，继续往上比较child = parent;parent = (child - 1) / 2;}else{break; // 已经满足大堆性质}}}public:// 无参构造：构造一个空堆priority_queue() {}// 区间构造：将 [begin, end) 区间内的数据建堆template<typename InputIterator>priority_queue(InputIterator begin, InputIterator end){while (begin != end){_con.push_back(*begin);++begin;}// 从最后一个非叶子结点开始，依次向下调整，建堆for (int i = (_con.size() - 2) / 2; i >= 0; --i){adjust_down(i);}}// 插入元素：尾插，然后向上调整void push(const T& val){_con.push_back(val);adjust_up(_con.size() - 1);}// 删除堆顶元素：首尾交换 → 删除尾元素 → 向下调整void pop(){if (_con.empty()) return; // 空堆不操作std::swap(_con[0], _con[_con.size() - 1]);_con.pop_back();if (!_con.empty()){adjust_down(0); // 从根结点开始向下调整}}// 访问堆顶元素（只读引用）const T& top() const{return _con.front();}// 判断堆是否为空bool empty() const{return _con.empty();}// 获取堆的大小size_t size() const{return _con.size();}private:Container _con; // 底层容器，默认用 vector 存储};
}

2. .c文件

#include"priority.h"namespace dh
{void test01(){int arr[] = { 5,20,13,14 };priority_queue<int> pq(arr, arr + sizeof(arr) / sizeof(arr[0]));pq.push(666);pq.push(88);pq.push(520);pq.push(1314);std::cout << pq.top() << std::endl;std::cout << pq.empty() << std::endl;std::cout << pq.size() << std::endl;while (!pq.empty()){std::cout << pq.top() << ' ';pq.pop();}std::cout << std::endl;}}int main()
{dh::test01();return 0;
}

3. 结果

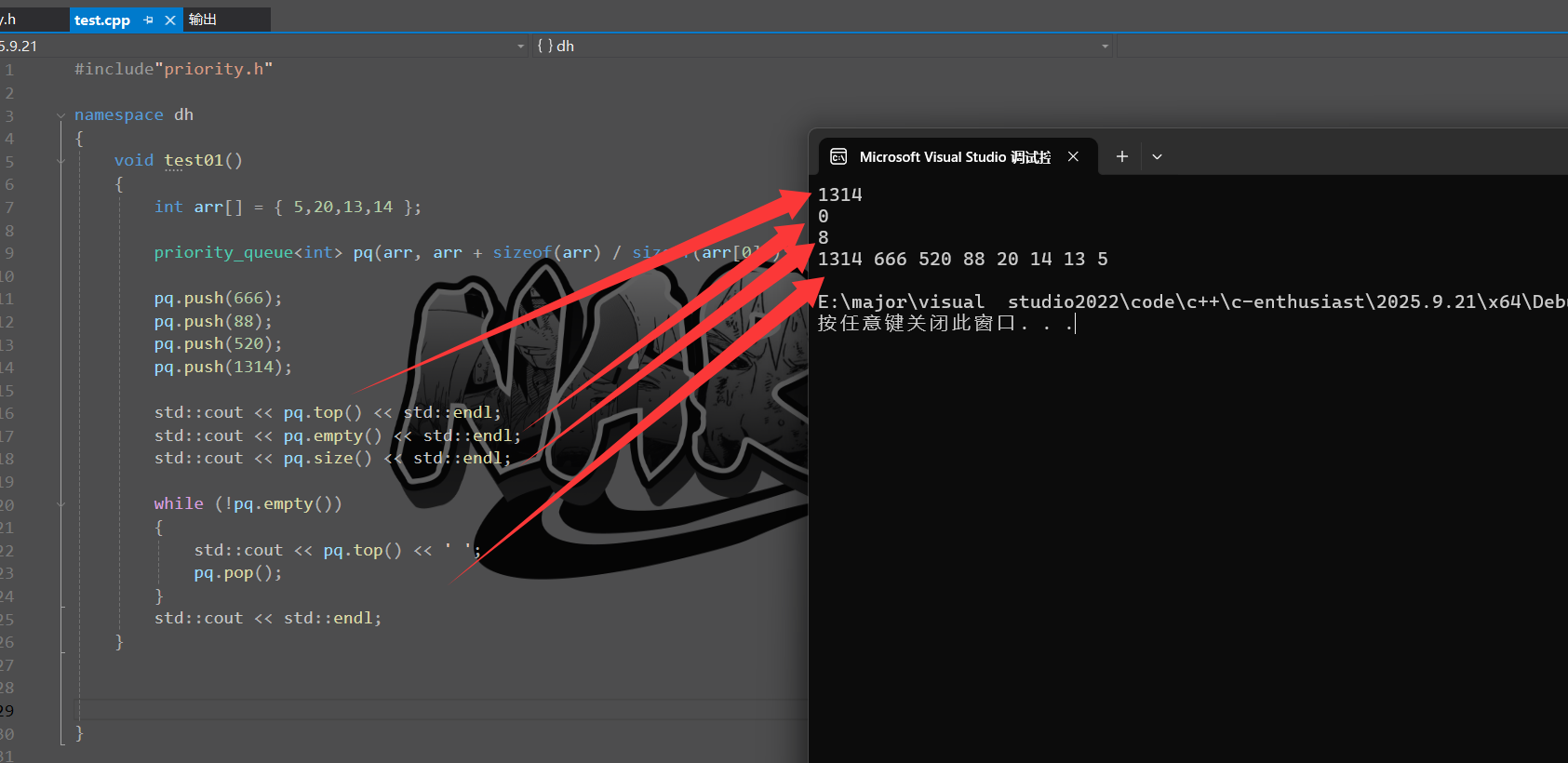
👌可以，基于你这篇文章的风格，我给你写一个简洁又专业的 摘要 和 结尾，直接粘贴到 CSDN 就能用。

---

结尾

本文带你从 STL 的 接口使用 到 底层堆实现，完整地认识了 priority_queue。它不仅是一个“用起来方便”的容器，更是许多算法（如 Dijkstra、Prim、Huffman 编码等）的核心工具。理解其本质，有助于我们在面对复杂问题时灵活选择合适的数据结构。
💡 建议大家在写题或项目中多用 priority_queue 练手，逐渐养成“优先级队列思维”，相信你会在算法和工程开发中走得更快更远 🚀。

---

不是呆头将一直坚持用清晰易懂的图解 + 代码语言，让每个知识点变得简单！
👁️ 【关注】 看一个非典型程序员如何用野路子解决正经问题
👍 【点赞】 给“不写八股文”的技术分享一点鼓励
🔖 【收藏】 把这些“奇怪但有用”的代码技巧打包带走
💬 【评论】 来聊聊——你遇到过最“呆头”的 Bug 是啥？
🗳️ 【投票】 您的投票是支持我前行的动力
技术没有标准答案，让我们一起用最有趣的方式，写出最靠谱的代码！ 🎮💻