Python9-逻辑回归-决策树

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

1. 逻辑回归介绍

逻辑回归的应⽤场景
⼴告点击率：有没有点击
是否为垃圾邮件
是否患病
是否⾦融诈骗
是否虚假账号

都是两个类别的问题–》二分类

所以逻辑回归的输入就是线性回归的输出

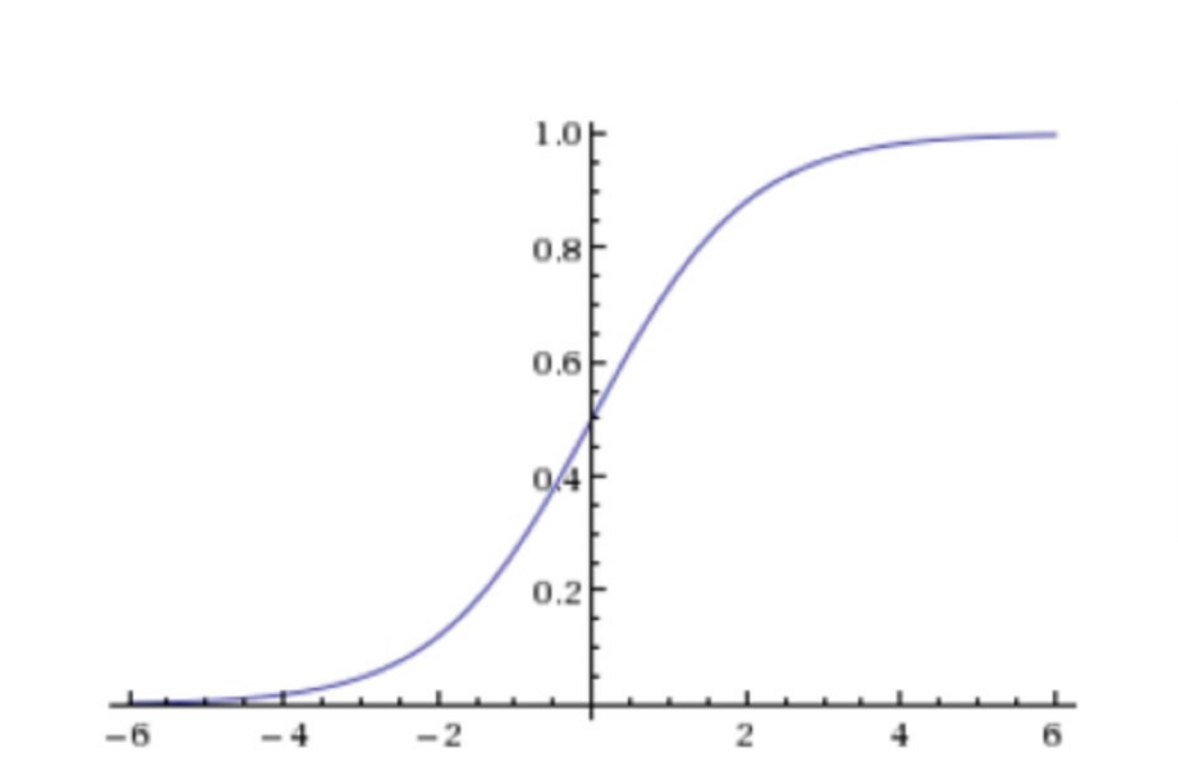
意思就是不管线性回归的值是什么范围，都会映射到0~1

默认是以0.5 进行区分，分类的
在逻辑回归中，当预测结果不对的时候，我们该怎么衡量其损失呢？
设置阈值为0.6

那么如何去衡量逻辑回归的预测结果与真实结果的差异呢？
线性回归用的是方差来衡量

1.1 损失

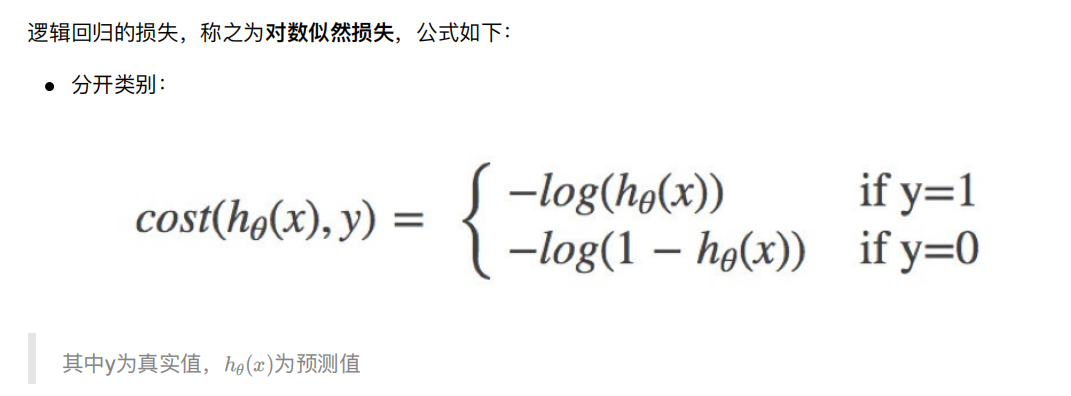
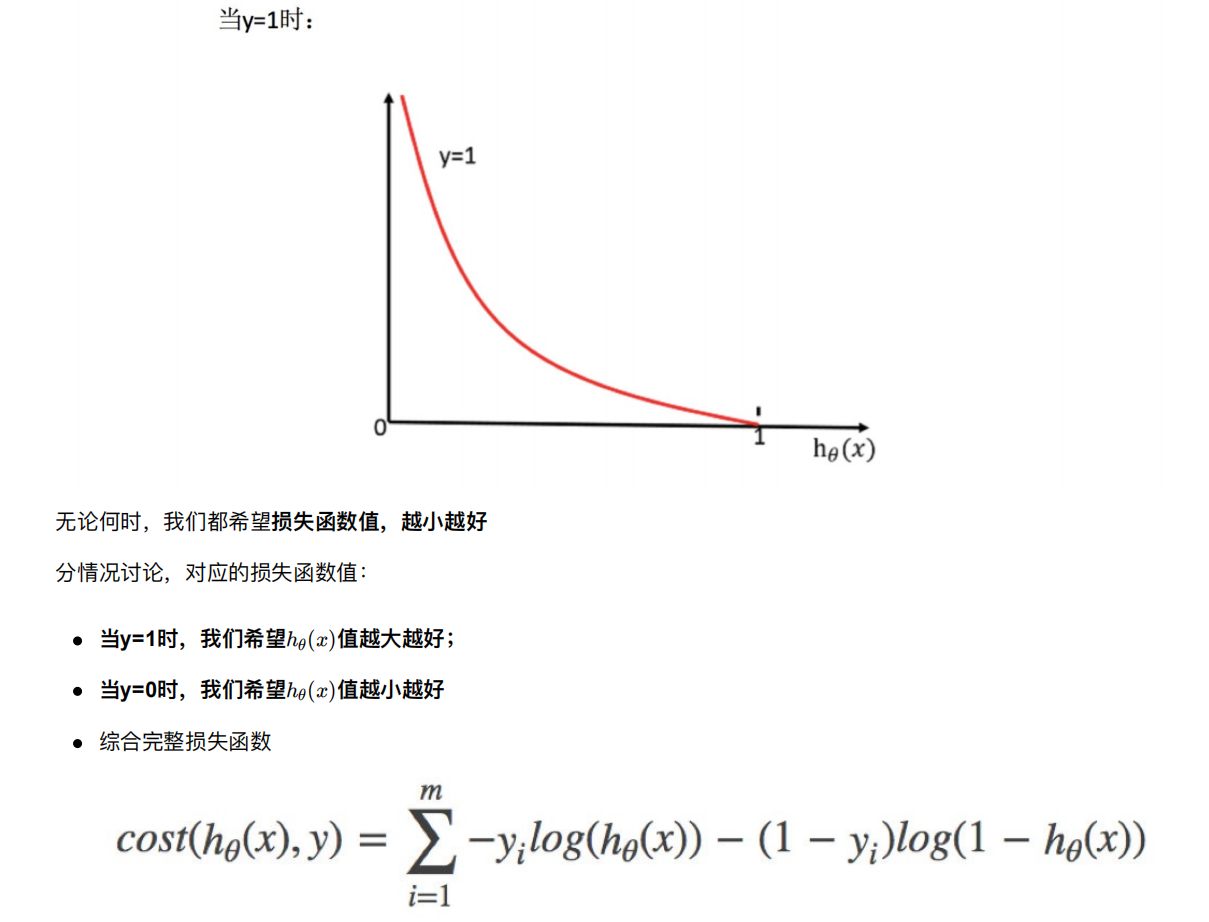
1.2 优化

同样使⽤梯度下降优化算法，去减少损失函数的值。这样去更新逻辑回归前⾯对应算法的权重参数，提升原本属于1类
别的概率，降低原本是0类别的概率。

2. 逻辑回归api介绍

sklearn.linear_model.LogisticRegression(solver='liblinear', penalty=‘l2’, C = 1.0)solver可选参数:{'liblinear', 'sag', 'saga','newton-cg', 'lbfgs'}，默认: 'liblinear'；⽤于优化问题的算法。对于⼩数据集来说，“liblinear”是个不错的选择，⽽“sag”和'saga'对于⼤型数据集会更快。对于多类问题，只有'newton-cg'， 'sag'， 'saga'和'lbfgs'可以处理多项损失;“liblinear”仅限于“one-versusrest”分		类。penalty：正则化的种类C：正则化⼒度

默认将类别数量少的当做正例
LogisticRegression⽅法相当于 SGDClassifier(loss=“log”, penalty=" "),SGDClassifier实现了⼀个普通的随机梯度
下降学习。⽽使⽤LogisticRegression(实现了SAG)

3. 案例：癌症分类预测-良／恶性乳腺癌肿瘤预测

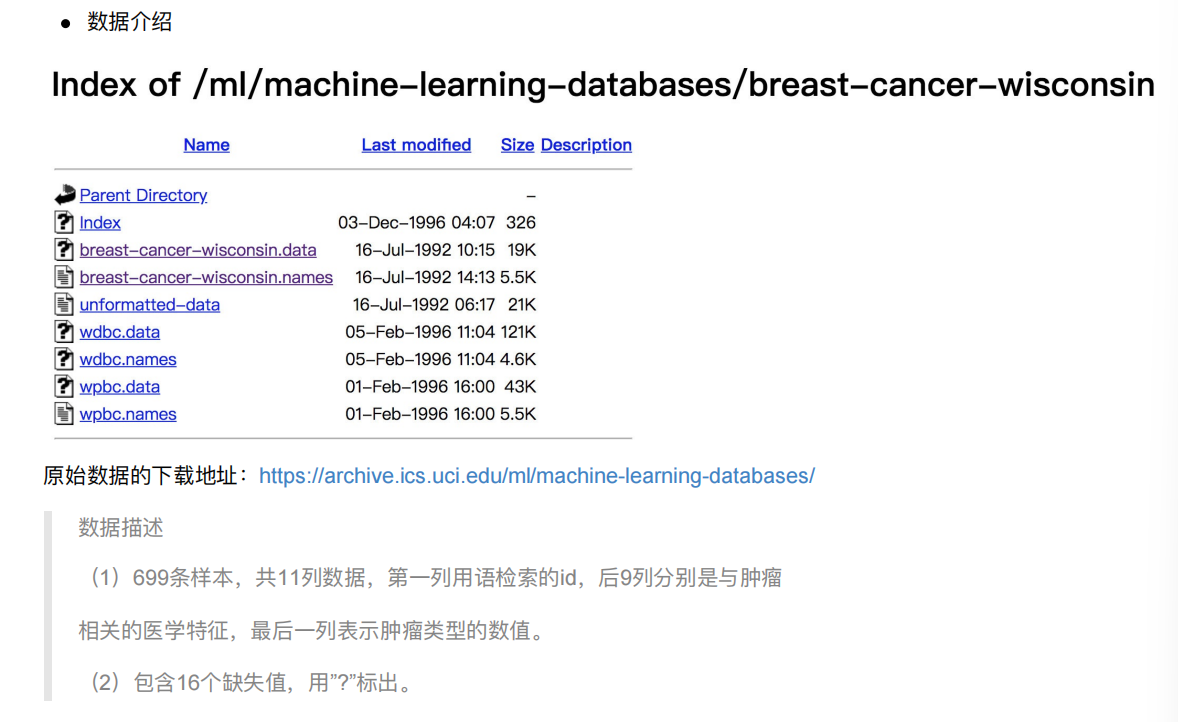
import pandas as pd
data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data")
data

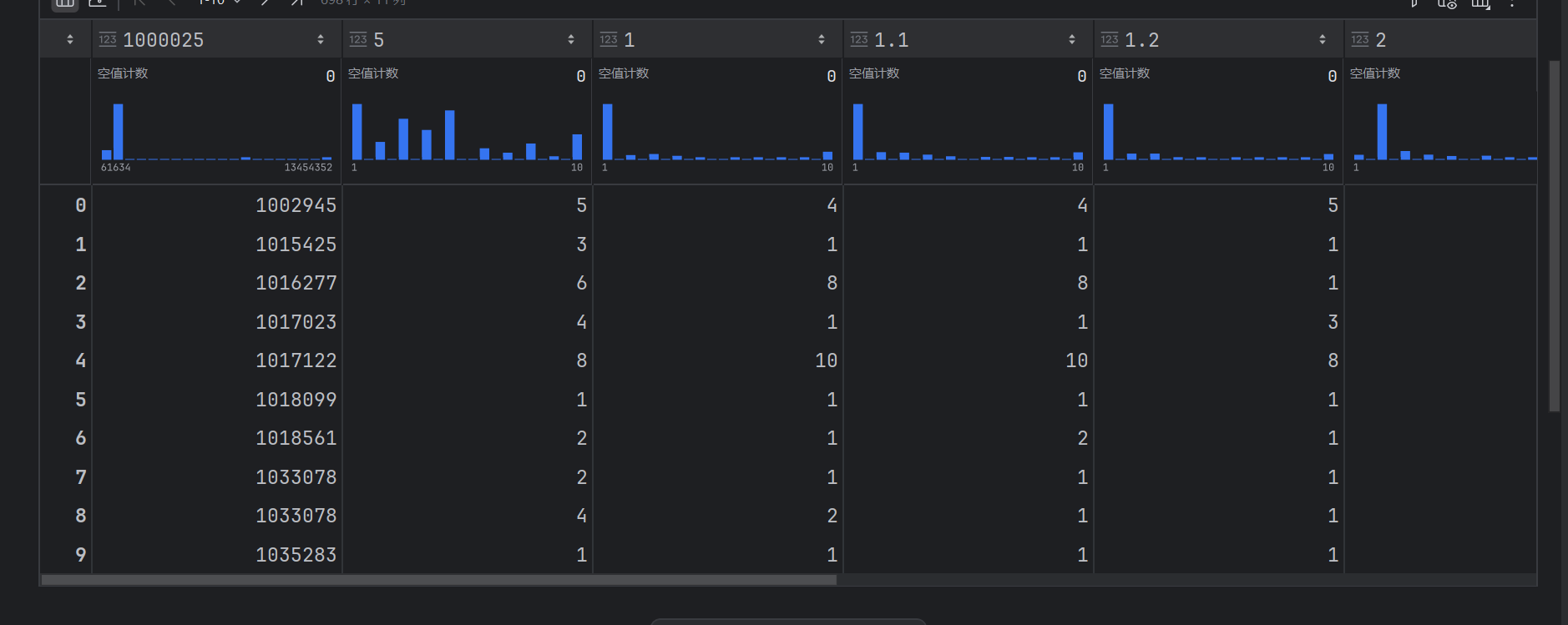
我们发现第一行竟然不是列名，而是数字

# 1.获取数据
names = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin',
'Normal Nucleoli', 'Mitoses', 'Class']
data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data",names=names)
data

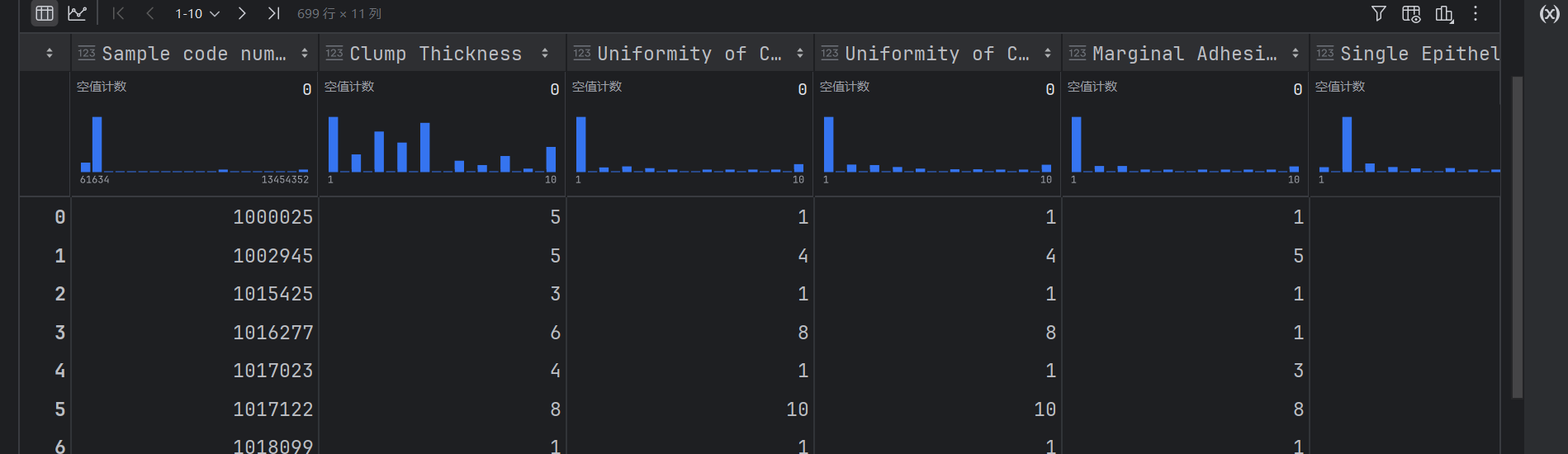
这样就可以了

# 2.基本数据处理
# 2.1 缺失值处理
# 2.2 确定特征值,⽬标值
# 2.3 分割数据
# 3.特征⼯程(标准化)
# 4.机器学习

#获取数据
import pandas as pd
# 数据处理
import numpy as np
#分割数据
from sklearn.model_selection import train_test_split
#标准化
from sklearn.preprocessing import StandardScaler
#逻辑回归
from sklearn.linear_model import LogisticRegression

# 2.基本数据处理
# 2.1 缺失值处理
data=data.replace(to_replace='?',value=np.nan)
data=data.dropna()

最后一列就是目标值
其他的，除了所以就是特征值

# 2.2 确定特征值,⽬标值
x=data.iloc[:,1:-1]
y = data["Class"]

# 2.3 分割数据
x_train,x_test,y_train,y_test =train_test_split(x,y,test_size=0.2,random_state=22)

# 3.特征⼯程(标准化)
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4.机器学习(逻辑回归)
estimator = LogisticRegression()
estimator.fit(x_train,y_train)

#5. 模型评估
#5.1 准确率
ret = estimator.score(x_test,y_test)
print("准确率为：\n",ret)
#5.2 预测值
y_predict = estimator.predict(x_test)
print("预测值为:\n",y_predict)

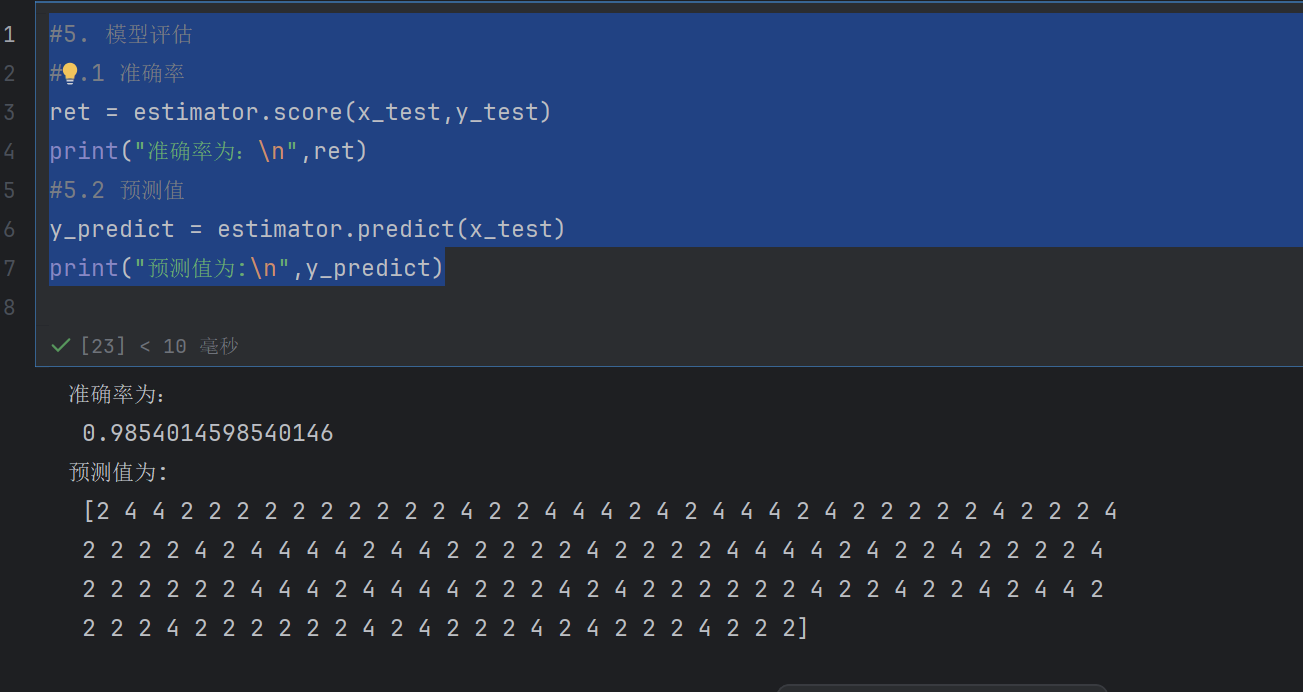
在很多分类场景当中我们不⼀定只关注预测的准确率！！！！！
⽐如以这个癌症举例⼦！！！我们并不关注预测的准确率，⽽是关注在所有的样本当中，癌症患者有没有被全部预测
（检测）出来。

4. 分类评估⽅法

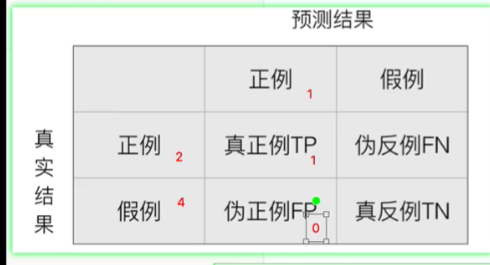
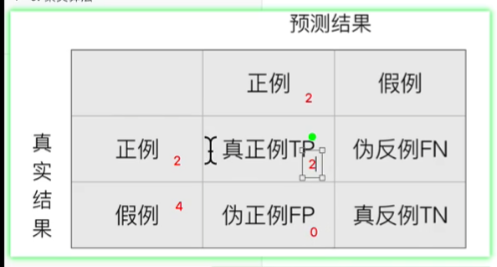
4.1 混淆矩阵

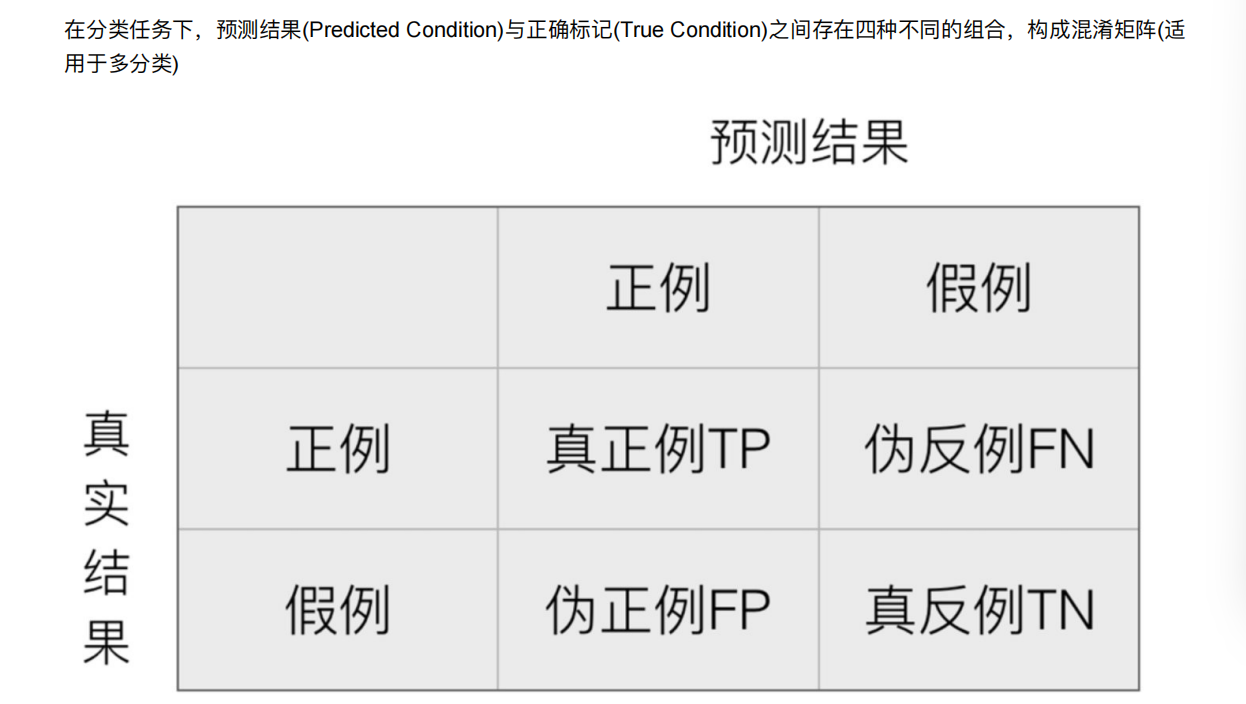
只有第真正例和真反例是预测对的

T是true
F是false
P是positive
N是negative

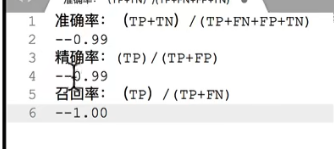
4.2 精确率(Precision)与召回率(Recall)与f1-score

精确率：预测结果为正例样本中真实为正例的⽐例（了解）

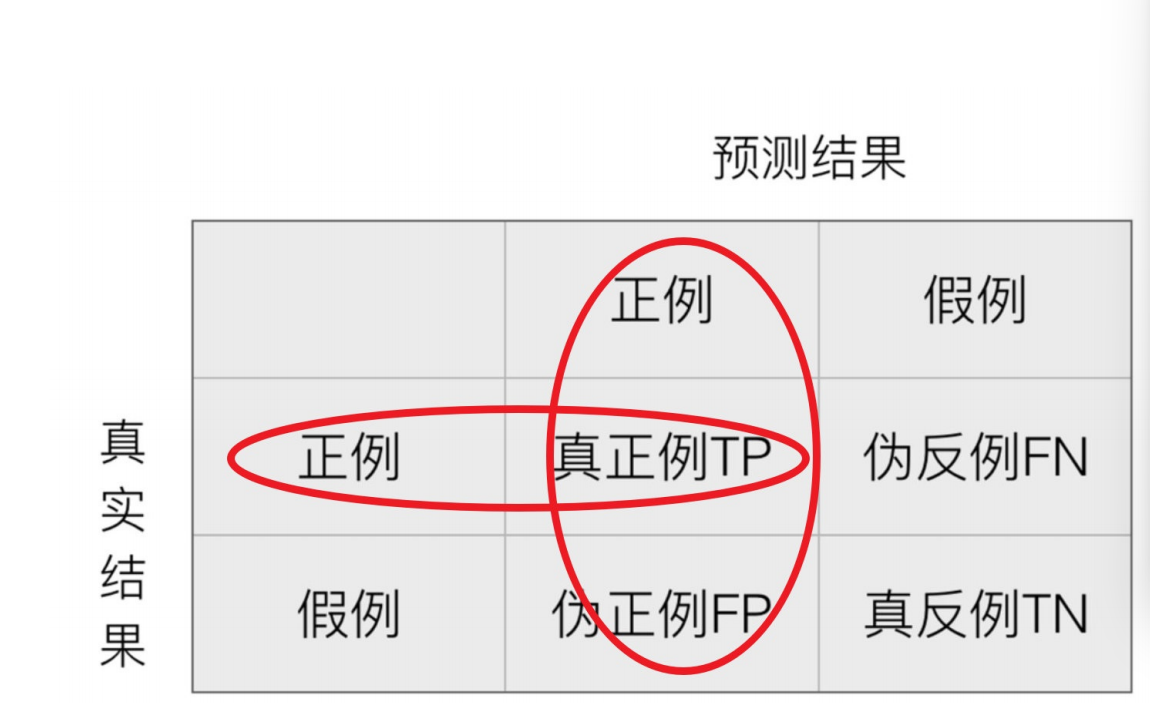
召回率：真实为正例的样本中预测结果为正例的⽐例（查得全，对正样本的区分能⼒）

其实正例和假例就是我们说的两种类别

4.3 分类评估报告api

sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None )y_true：真实⽬标值y_pred：估计器预测⽬标值labels:指定类别对应的数字target_names：⽬标类别名称return：每个类别精确率与召回率

ret = classification_report(y_test, y_predict, labels=(2,4), target_names=("良性", "恶性"))
print(ret)

from sklearn.metrics import classification_report

#5.3 精确率召回率，指标评价
ret=classification_report(y_test,y_predict)
print(ret)

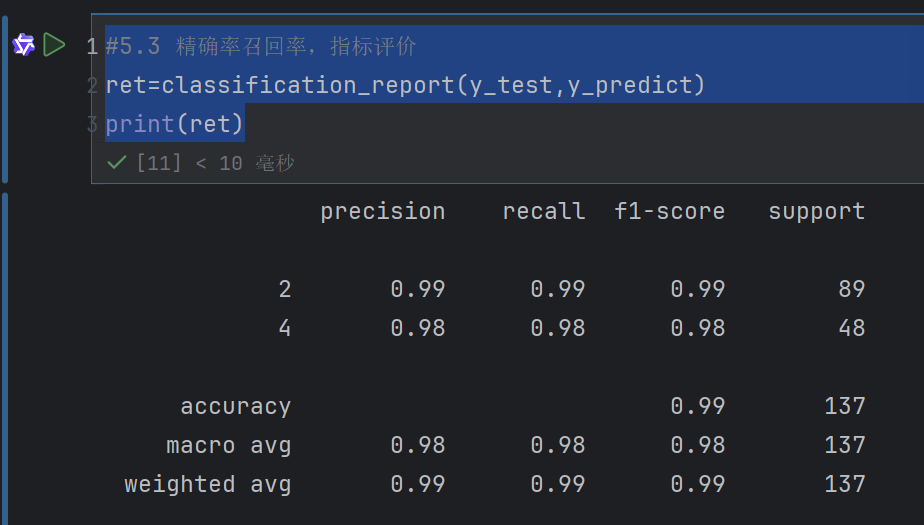
但是不知道2和4是什么意思

#5.3 精确率召回率，指标评价
ret=classification_report(y_test,y_predict,labels=[2,4],target_names=["良性","恶性"])
print(ret)

这样意思就是有两个目标值，一个2代表良性，一个4代表恶性

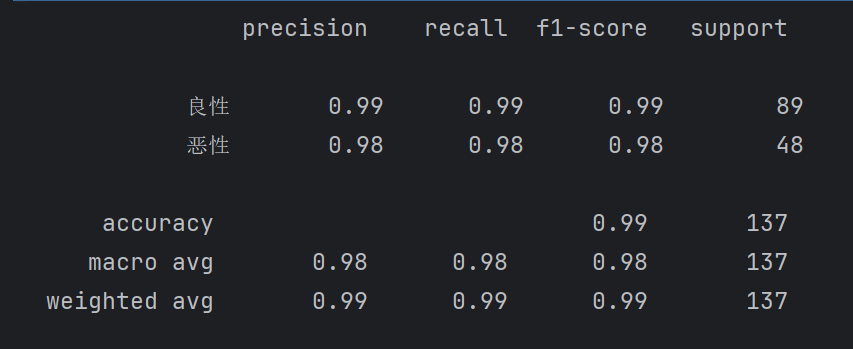
precision是精确率
recall是召回率

f1-score（F1 分数）是精确率（precision）和召回率（recall）的调和平均值

support 表示对应类别在测试数据集中的实际样本数量

恶性的recall的0.98表示100个恶性中，我们查出来了98个恶性

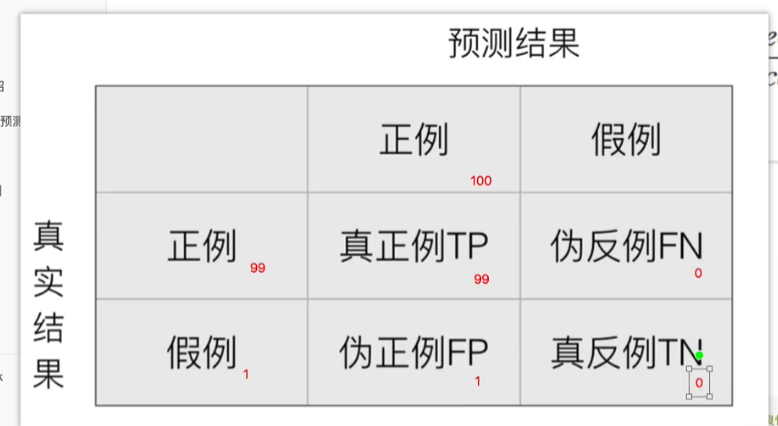
假设这样⼀个情况，如果99个样本癌症，1个样本⾮癌症，不管怎样我全都预测正例(默认癌症为正例),准确率就为99%
但是这样效果并不好，这就是样本不均衡下的评估问题—》就是数据比例不均衡，两种数据比例相差太大，4:1，5:1

4.4 ROC曲线与AUC指标

TPR = TP / (TP + FN)
所有真实类别为1的样本中，预测类别为1的⽐例
FPR = FP / (FP + TN)
所有真实类别为0的样本中，预测类别为1的⽐例
TPR 就是召回率
FPR 什么都不是

ROC曲线的横轴就是FPRate，纵轴就是TPRate，当⼆者相等时，表示的意义则是：对于不论真实类别是1还是0的
样本，分类器预测为1的概率是相等的，此时AUC为0.5

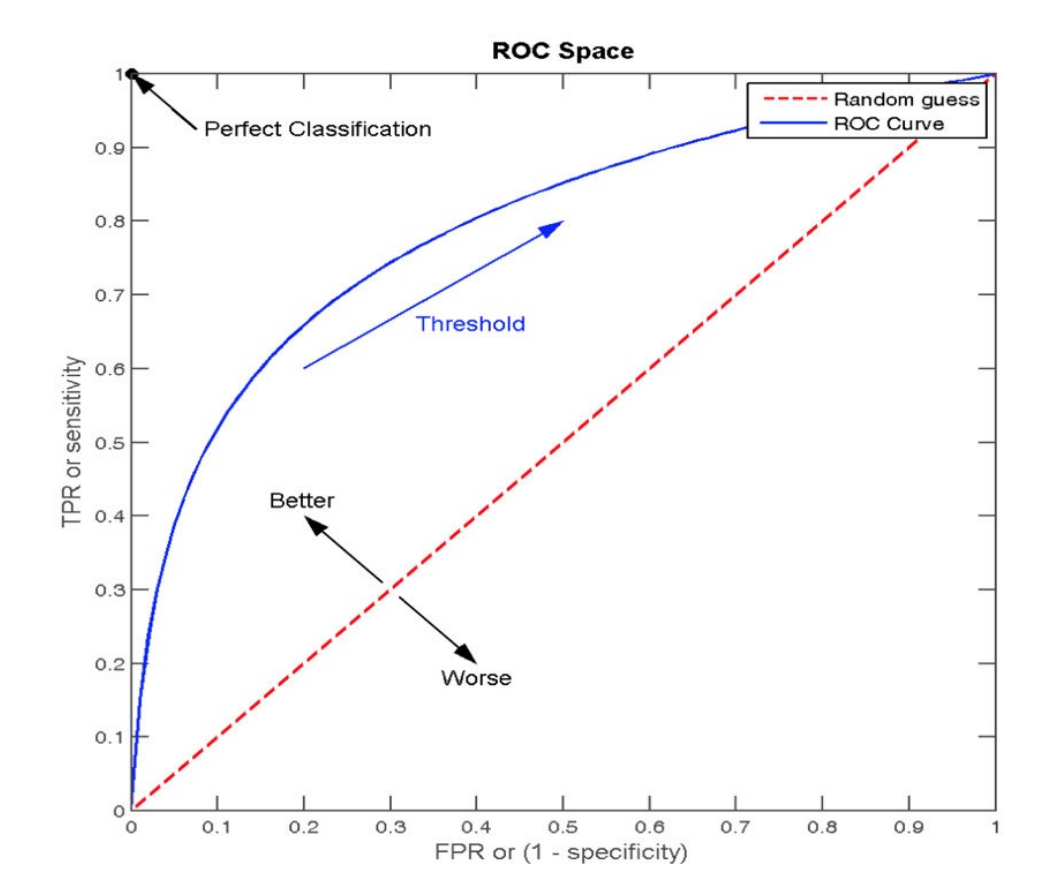
（0,1）这个点表示的是：TPR=1,FPR=0
意思就是真实类别为1的样本中，所有都预测为1
真实类别为0的样本中，所有都预测为0
那么就是全部预测正确了
（1,0）
意思就是全部预测错了

所以偏上的正确率高

中间红线的意思就是，不管什么类别样本，预测1的比例都一样—》乱猜

AUC指标：
AUC的概率意义是随机取⼀对正负样本，正样本得分⼤于负样本得分的概率
AUC的范围在[0, 1]之间，并且越接近1越好，越接近0.5属于乱猜
AUC=1，完美分类器，采⽤这个预测模型时，不管设定什么阈值都能得出完美预测。绝⼤多数预测的场合，不存
在完美分类器。
0.5<AUC<1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值

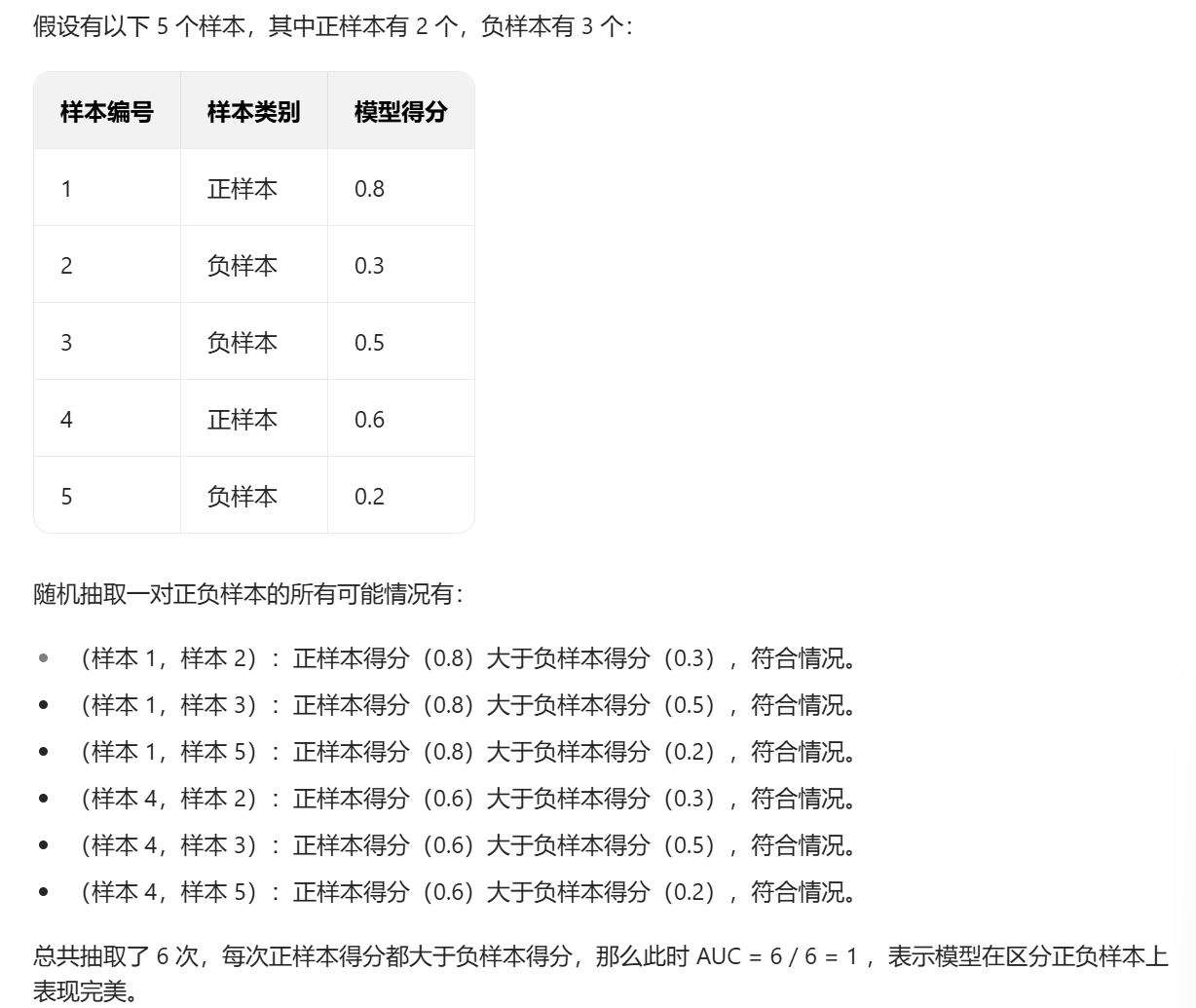
一般来说，AUC 的取值范围在 0.5 到 1 之间，AUC = 0.5 表示模型的预测结果完全是随机的，没有区分正负样本的能力；AUC 越接近 1，说明模型区分正负样本的能力越强。

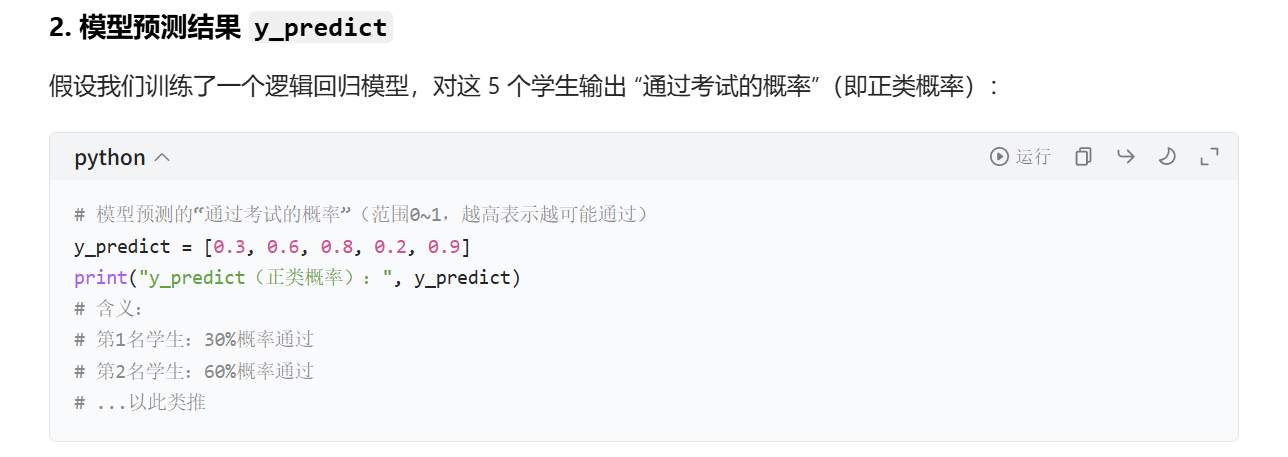
4.5 AUC计算API

from sklearn.metrics import roc_auc_scoresklearn.metrics.roc_auc_score(y_true, y_score)计算ROC曲线⾯积，即AUC值y_true：每个样本的真实类别，必须为0(反例),1(正例)标记y_score：预测得分，可以是正类的估计概率、置信值或者分类器⽅法的返回值

y_test=np.where(y_test>3,1,0)

这个是把测试值的特征值全部变为0和1

from sklearn.metrics import classification_report,roc_auc_score

y_test=np.where(y_test>3,1,0)
roc_auc_score(y_test,y_predict)

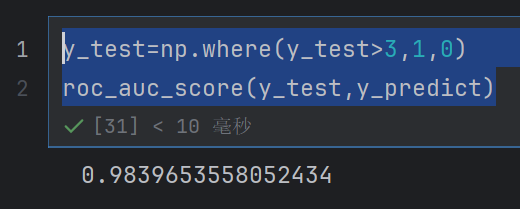
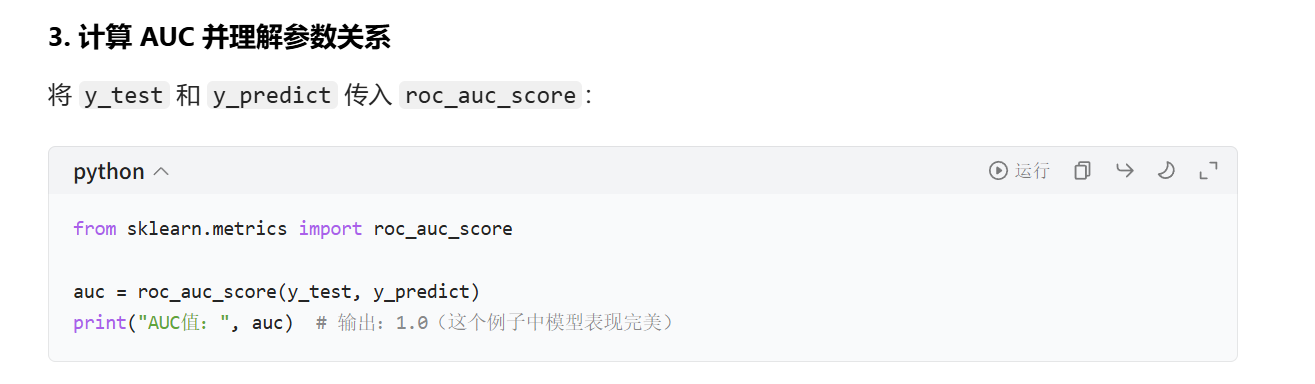
反正意思就是y_test表示我们已经知道了谁是负样本，谁是正样本
那么就去y_predict里面去取值，按照y_test去取值，取一个正的样本（4）和一个负样本（2），在y_predict中正样本大于负样本的概率

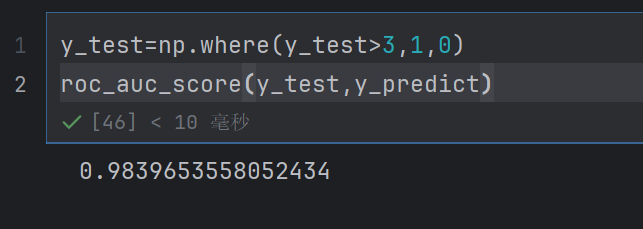
AUC只能⽤来评价⼆分类
AUC⾮常适合评价样本不平衡中的分类器性能

怎么解决的呢
如果100个中，实际99个好的，一个坏的
那么我们预测全部为好的，准确率是99%
但是auc呢
发现按照y_test取值
用y_predict比较—》auc=0—》非常不对–》
只要数据不平衡—》那些预测错了一两个—》auc就会很小了

5. ROC曲线的绘制

假设有6次展示记录，有两次被点击了，得到⼀个展示序列（1:1,2:0,3:1,4:0,5:0,6:0），前⾯的表示序号，后⾯的表示
点击（1）或没有点击（0）。
然后在这6次展示的时候都通过model算出了点击的概率序列。

如果概率的序列是（1:0.9,2:0.7,3:0.8,4:0.6,5:0.5,6:0.4），表示每个点被点击概率

这个就表示概率，对应有没有被点击
发现高概率的都被点击了

我们把1表示正例，0表示反例
所以两个正例，四个反例

这个是取了一个点的时候

这个是取两点的时候

这个是取三个点作为正例

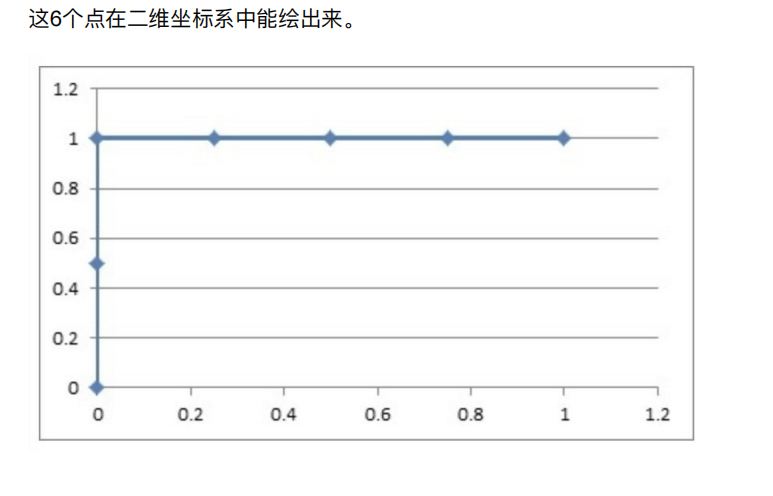
然后把这6对数据组成6个点(0,0.5),(0,1.0),(0.25,1),(0.5,1),(0.75,1),(1.0,1.0)。
这6个点在⼆维坐标系中能绘出来。

精确率：预测结果为正例样本中真实为正例的⽐例
召回率：真实为正例的样本中预测结果为正例的⽐例（查得全，对正样本的区分能⼒）

TPR = TP / (TP + FN)，纵坐标
所有真实类别为1的样本中，预测类别为1的⽐例
FPR = FP / (FP + TN)，横坐标
所有真实类别为0的样本中，预测类别为1的⽐例
TPR 就是召回率

什么意思呢，意思就是我们把特征值的预测值变为0~1的数字，就是我们上面说的概率0.9,0.8这些
所以说概率0.9其实就是预测值
然后判断这个预测值是什么类型1还是0
判断依据是我们设置的阈值
我们比如设置阈值为0.9
就预测值（概率，得分）表示大于等于0.9的，就是正例1，其他的就是假例
所以只有概率为0.9的才是预测的正例，也是实际的正例
所以才有了点（）

这样一直这样就成功了
所以计算ROC，需要0~1的得分，实际值类别也必须是0和1
但是计算AUC,类别是0和1，但是预测值可以不是0~1，因为auc只是把实际值对应的正例和反例的预测值进行比较大小而已

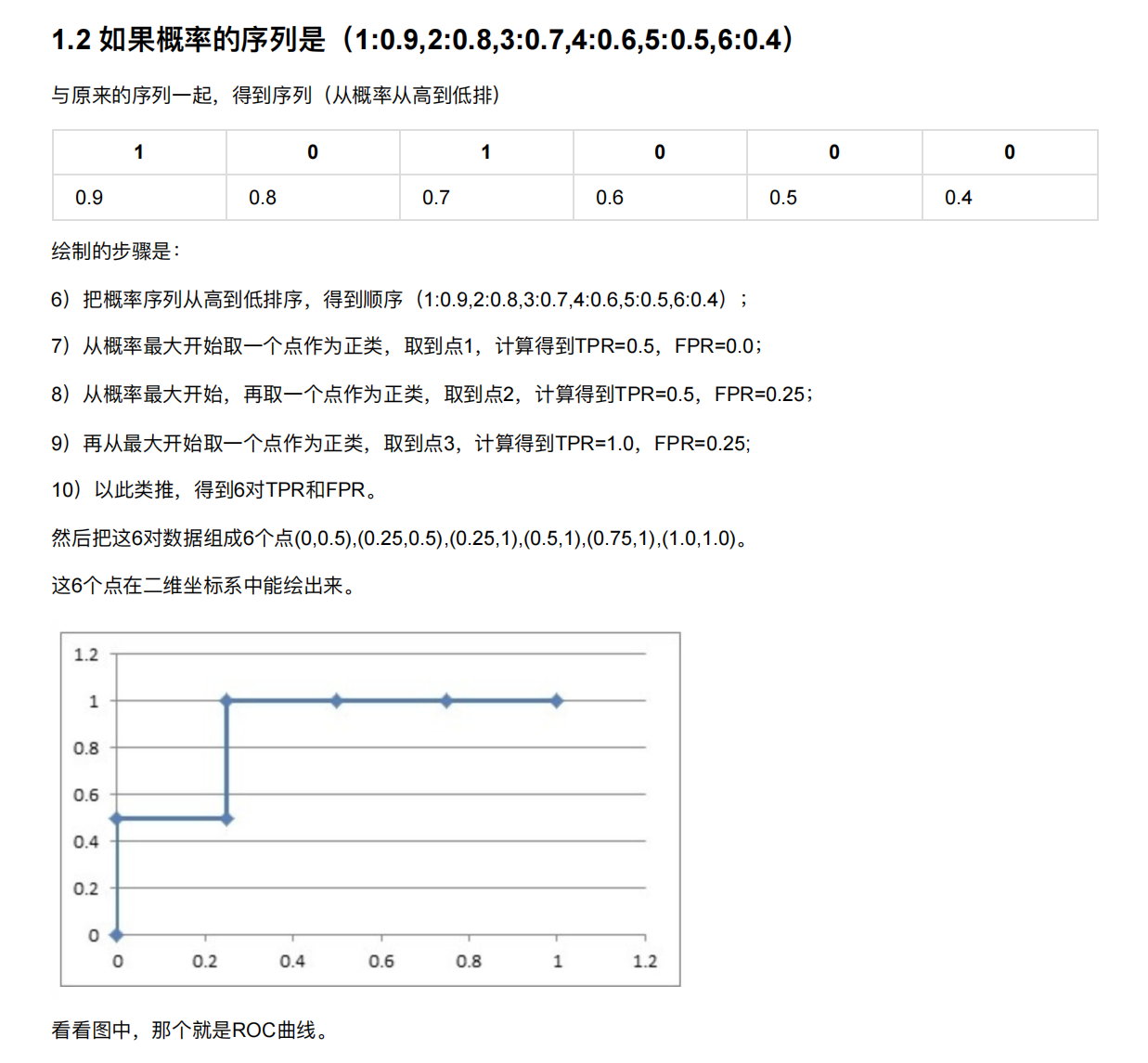
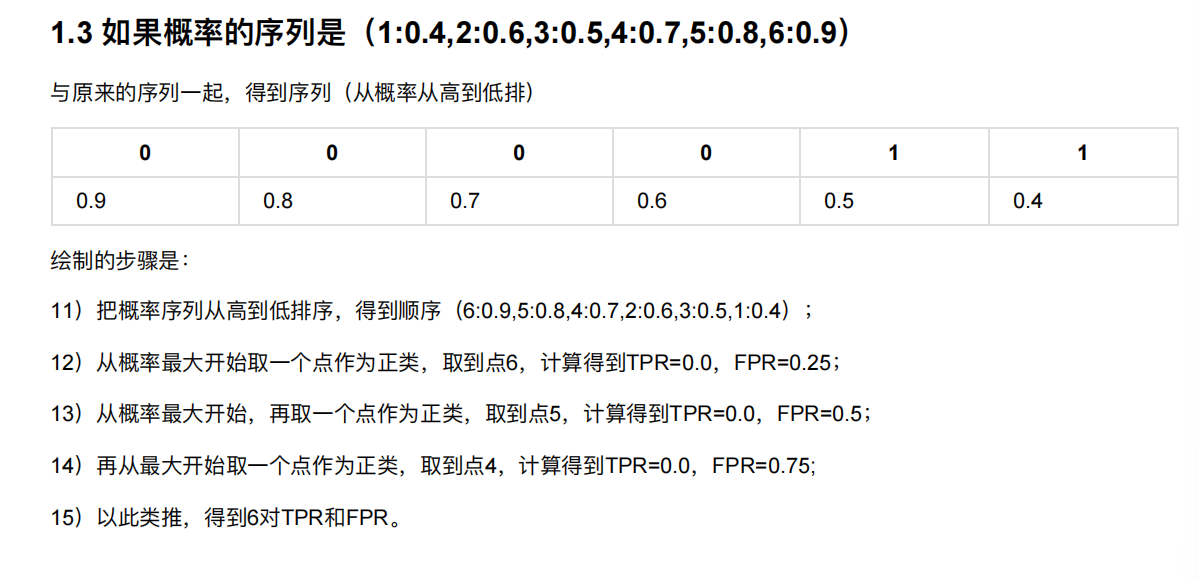
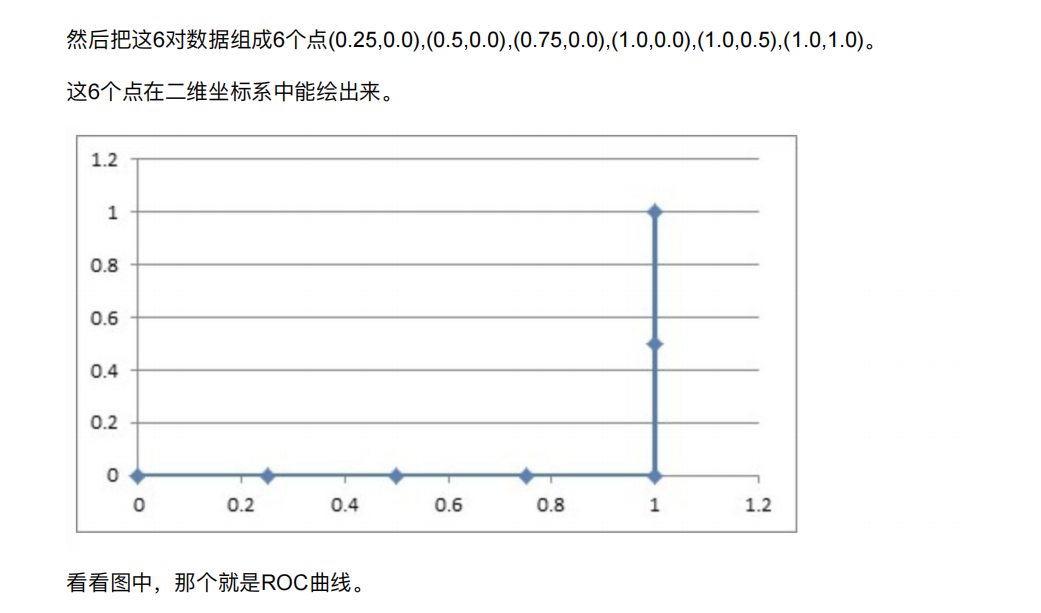
这个就表示完全分错了

我们发现积分面积越大就越好，而且面积是分好的概率

6. 分类中解决类别不平衡问题

在Python中，有Imblearn包，它就是为处理数据⽐例失衡⽽⽣的

conda install imbalanced-learn

from sklearn.datasets import make_classification
import matplotlib.pyplot as plt

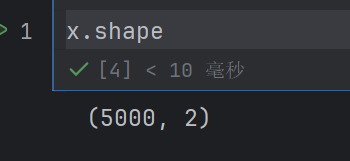
x,y = make_classification(n_samples=5000, n_features=2,  n_informative=2,n_redundant=0,n_repeated=0,n_classes=3,n_clusters_per_class=1, weights=[0.01,0.05,0.94],random_state=1)

make_classification 是 scikit-learn 中用于生成模拟分类数据集的函数

n_samples=5000：生成的样本总数为 5000 个。即最终生成的数据集包含 5000 条数据。

n_features=2：每个样本的特征数量为 2 个。即生成的数据集中有 2 个输入特征（自变量）

n_informative=2：有效特征的数量为 2 个。有效特征是指对分类有实际贡献、与类别相关的特征。这里与 n_features 相等，说明所有特征都是有效的

n_redundant=0：冗余特征的数量为 0 个。冗余特征是指由有效特征通过线性组合生成的无新信息的特征（例如，特征 3 = 0.5× 特征 1 + 0.3× 特征 2）

n_repeated=0：重复特征的数量为 0 个。重复特征是指从有效特征或冗余特征中复制的特征（完全相同的特征）。这里没有重复特征

n_classes=3：生成数据的类别数量为 3 个。即这是一个三分类问题，标签取值可能为 0、1、2（或其他整数）

n_clusters_per_class=1：每个类别包含的 “簇” 数量为 1 个。簇可以理解为类别内部的密集数据团，这里每个类别是一个紧凑的簇（如果增大该值，每个类别会分裂成多个子簇）
weights=[0.01, 0.05, 0.94]：各个类别的样本比例（权重）。
第一个类别占比 1%（约 50 个样本）；
第二个类别占比 5%（约 250 个样本）；
第三个类别占比 94%（约 4700 个样本）。
这是一个严重不平衡的数据集，第三个类别占绝大多数

random_state=1：随机数种子。设置固定值（如 1）可以保证每次运行代码生成的数据集完全相同，便于结果复现；若不设置，则每次生成的数据会不同

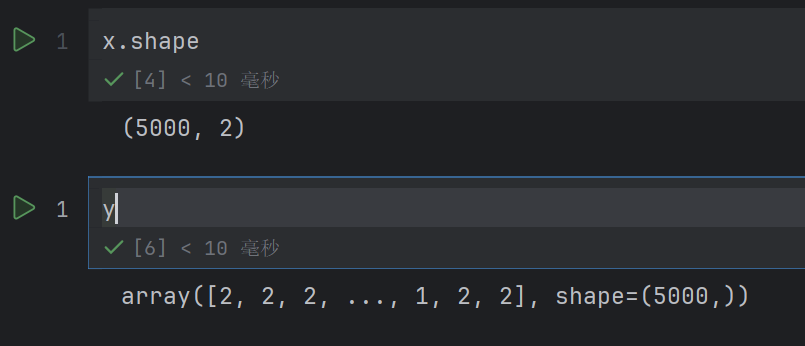
plt.scatter(x[:,0],x[:,1],c=y)
plt.show()

plt.scatter(x[:,0], x[:,1], c=y)
x[:,0]：取数据集x的第 1 个特征（所有样本的第 0 列数据），作为散点图的横轴坐标；
x[:,1]：取数据集x的第 2 个特征（所有样本的第 1 列数据），作为散点图的纵轴坐标；
c=y：用样本的标签y（类别）为散点着色，即不同类别的样本会显示不同颜色，便于直观区分类别。

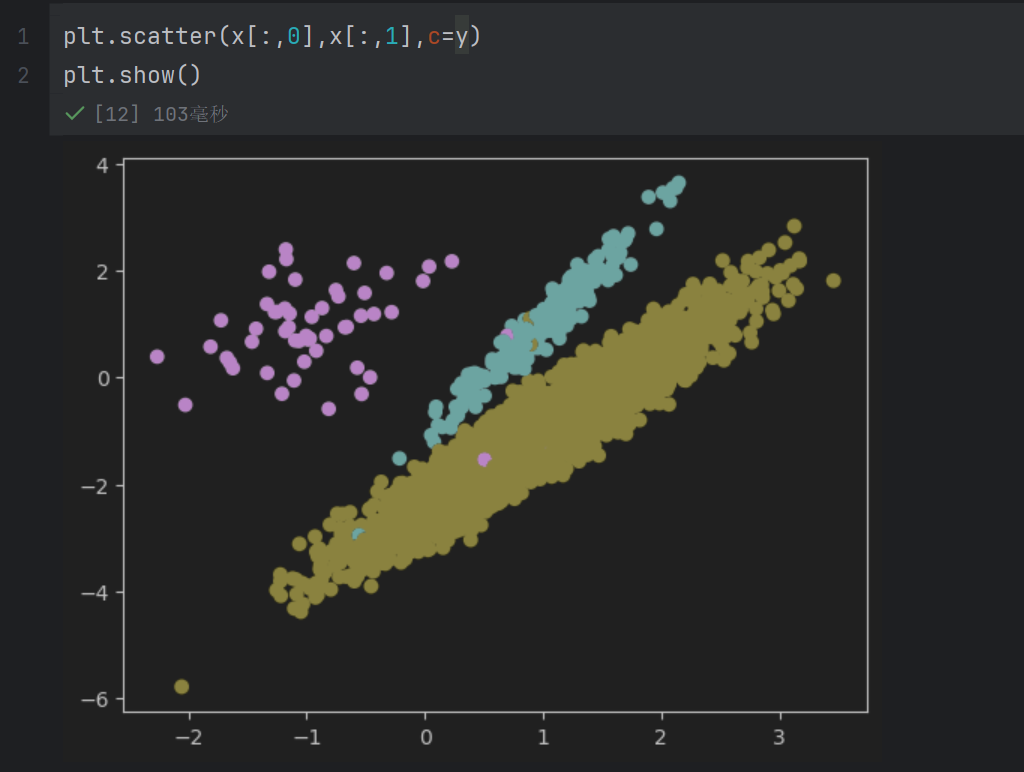
现在是准备类别不平衡数据
关于类别不平衡的问题，主要有两种处理⽅式：
过采样⽅法
增加数量较少那⼀类样本的数量，使得正负样本⽐例均衡。
⽋采样⽅法
减少数量较多那⼀类样本的数量，使得正负样本⽐例均衡。

6.1 过采样和⽋采样

6.2 随机过采样⽅法

对于随机过采样，由于需要对少数类样本进⾏复制来扩⼤数据集，造成模型训练复杂度加⼤。
另⼀⽅⾯也容易造成模型的过拟合问题，因为随机过采样是简单的对初始样本进⾏复制采样，这就使得学习器
学得的规则过于具体化，不利于学习器的泛化性能，造成过拟合问题

from collections import Counter

from imblearn.over_sampling import RandomOverSampler
ros = RandomOverSampler(random_state=0)
x_res,y_res = ros.fit_resample(x,y)

Counter(y_res)

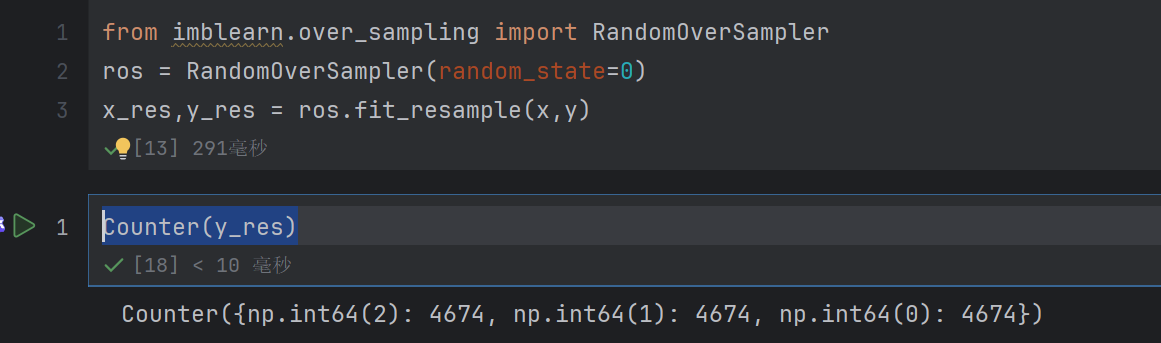
这样每个类别数量都差不多了

plt.scatter(x_res[:,0],x_res[:,1],c=y_res)
plt.show()

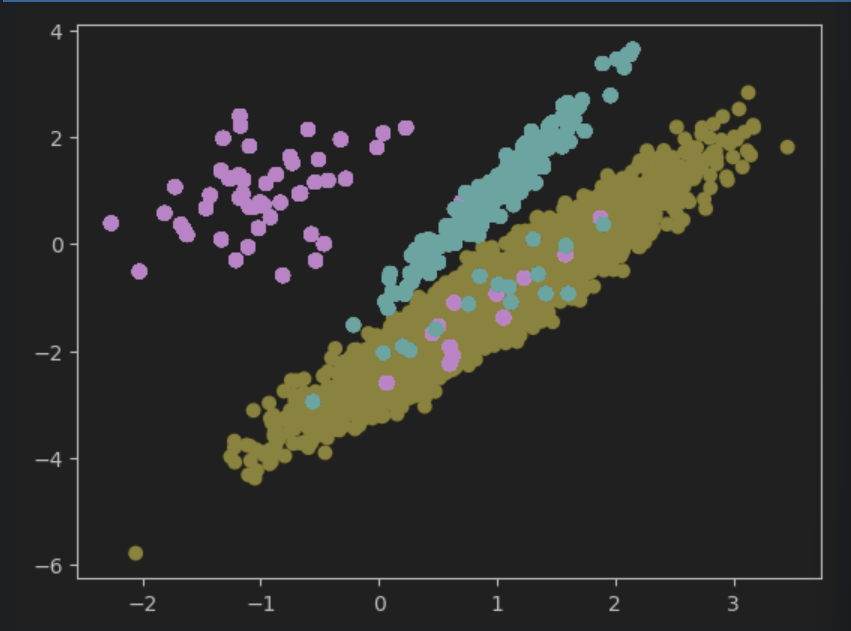
看着好像类别没有增加，但是其实是因为这个随机过采样方法是粘贴复制的方法，所以点就重复了很多很多

6.3 过采样代表性算法-SMOTE

SMOTE算法摒弃了随机过采样复制样本的做法，可以防⽌随机过采样中容易过拟合的问题，实践证明此⽅法可以提⾼
分类器的性能。

#Smote
from imblearn.over_sampling import SMOTE
smote = SMOTE(random_state=0)
x_res,y_res = smote.fit_resample(x,y)
Counter(y_res)

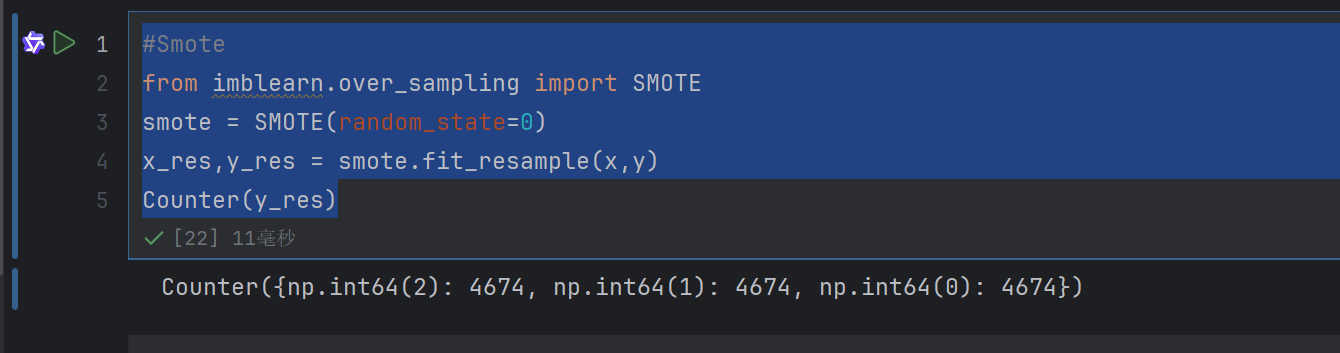
plt.scatter(x_res[:,0],x_res[:,1],c=y_res)
plt.show()

因为是在点与点之间找一个点，所以看着就像连线了，而且有效概率大，可能这个随机选的点还是真的这一类的，因为是连线选的嘛

6.4 随机⽋采样⽅法

随机⽋采样⽅法通过改变多数类样本⽐例以达到修改样本分布的⽬的，从⽽使样本分布较为均衡，但是这也存
在⼀些问题。对于随机⽋采样，由于采样的样本集合要少于原来的样本集合，因此会造成⼀些信息缺失，即将
多数类样本删除有可能会导致分类器丢失有关多数类的重要信息

#随机欠采样
from imblearn.under_sampling import RandomUnderSampler
rus = RandomUnderSampler(random_state=0)
x_res,y_res = rus.fit_resample(x,y)
Counter(y_res)

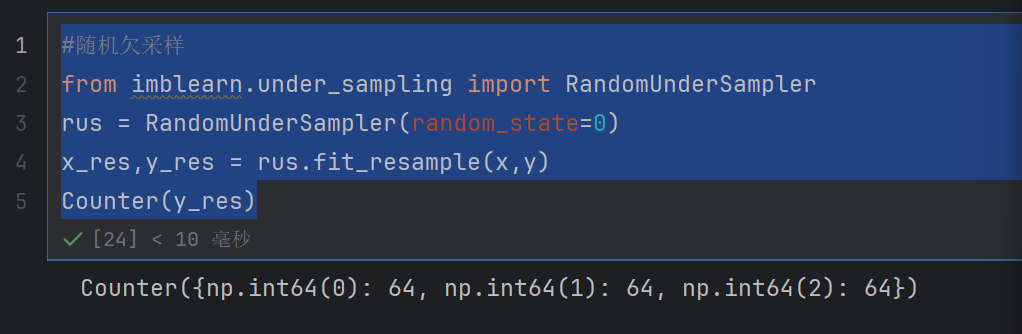
plt.scatter(x_res[:,0],x_res[:,1],c=y_res)
plt.show()

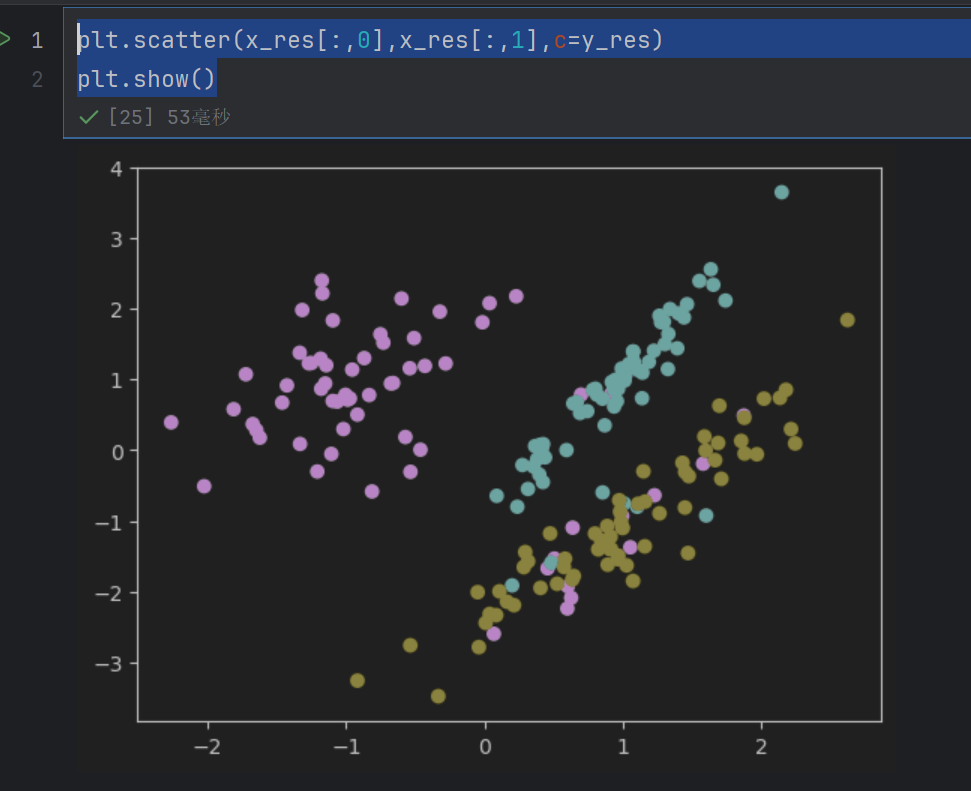
这个方法用的不是很多，因为删除了好多数据

7. 决策树算法简介

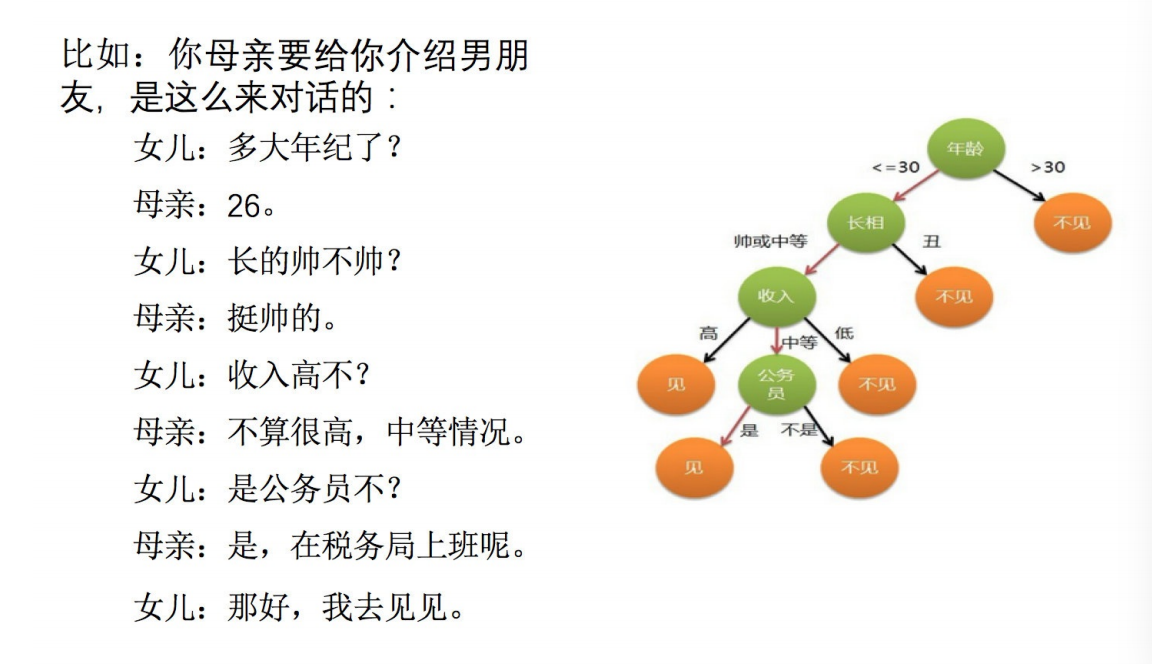
决策树：
是⼀种树形结构，本质是⼀颗由多个判断节点组成的树
其中每个内部节点表示⼀个属性上的判断，
每个分⽀代表⼀个判断结果的输出，
最后每个叶节点代表⼀种分类结果

8. 决策树分类原理

8.1 熵

信息熵

1、从信息的完整性上进⾏的描述:
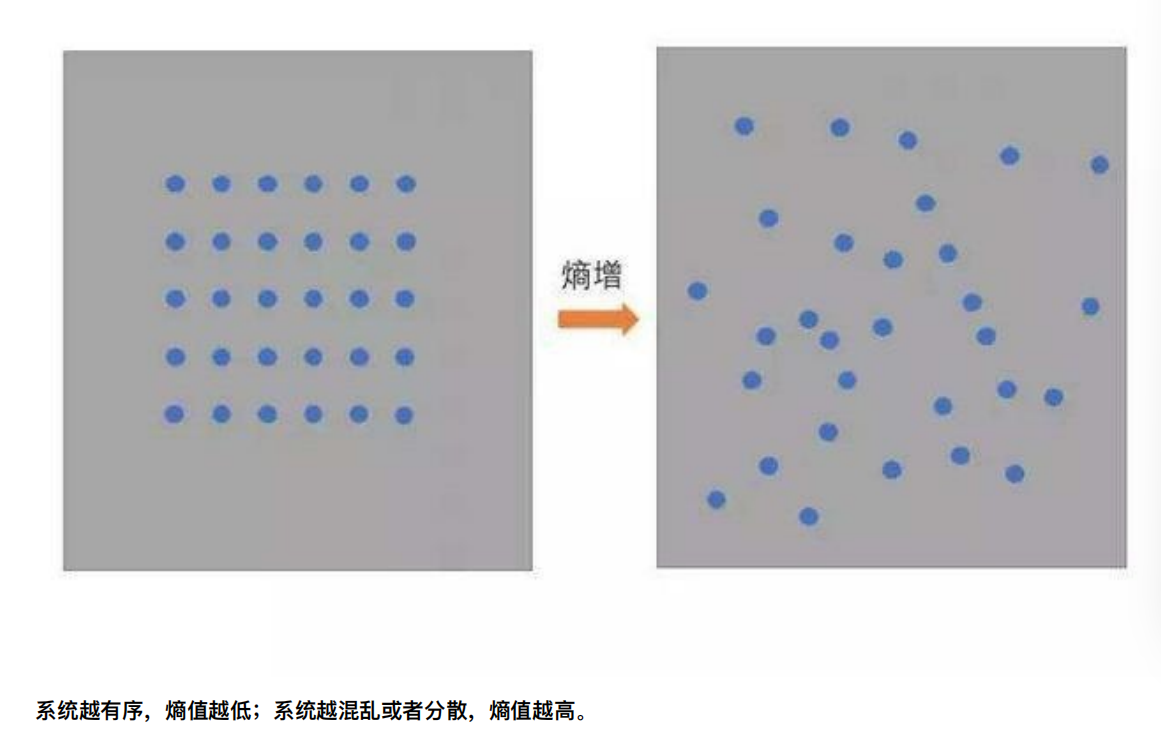
当系统的有序状态⼀致时，数据越集中的地⽅熵值越⼩，数据越分散的地⽅熵值越⼤。
2、从信息的有序性上进⾏的描述:
当数据量⼀致时，系统越有序，熵值越低；系统越混乱或者分散，熵值越⾼

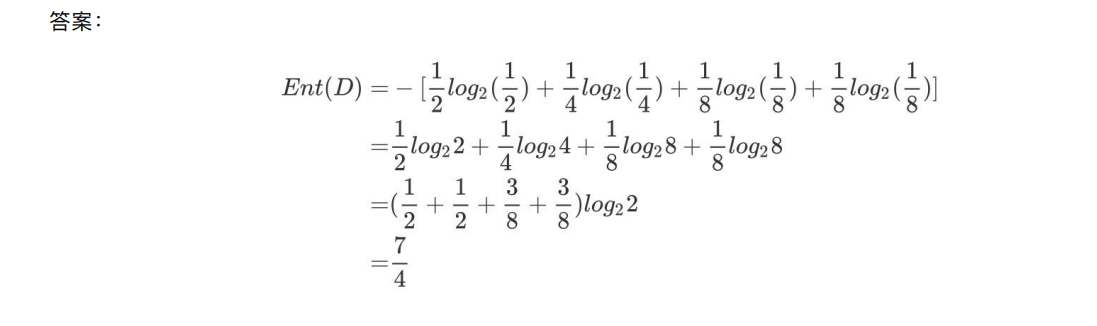
8.2 决策树的划分依据一----信息增益

信息增益：以某特征划分数据集前后的熵的差值。熵可以表示样本集合的不确定性，熵越⼤，样本的不确定性就越⼤。
因此可以使⽤划分前后集合熵的差值来衡量使⽤当前特征对于样本集合D划分效果的好坏
信息增益 = entroy(前) - entroy(后)

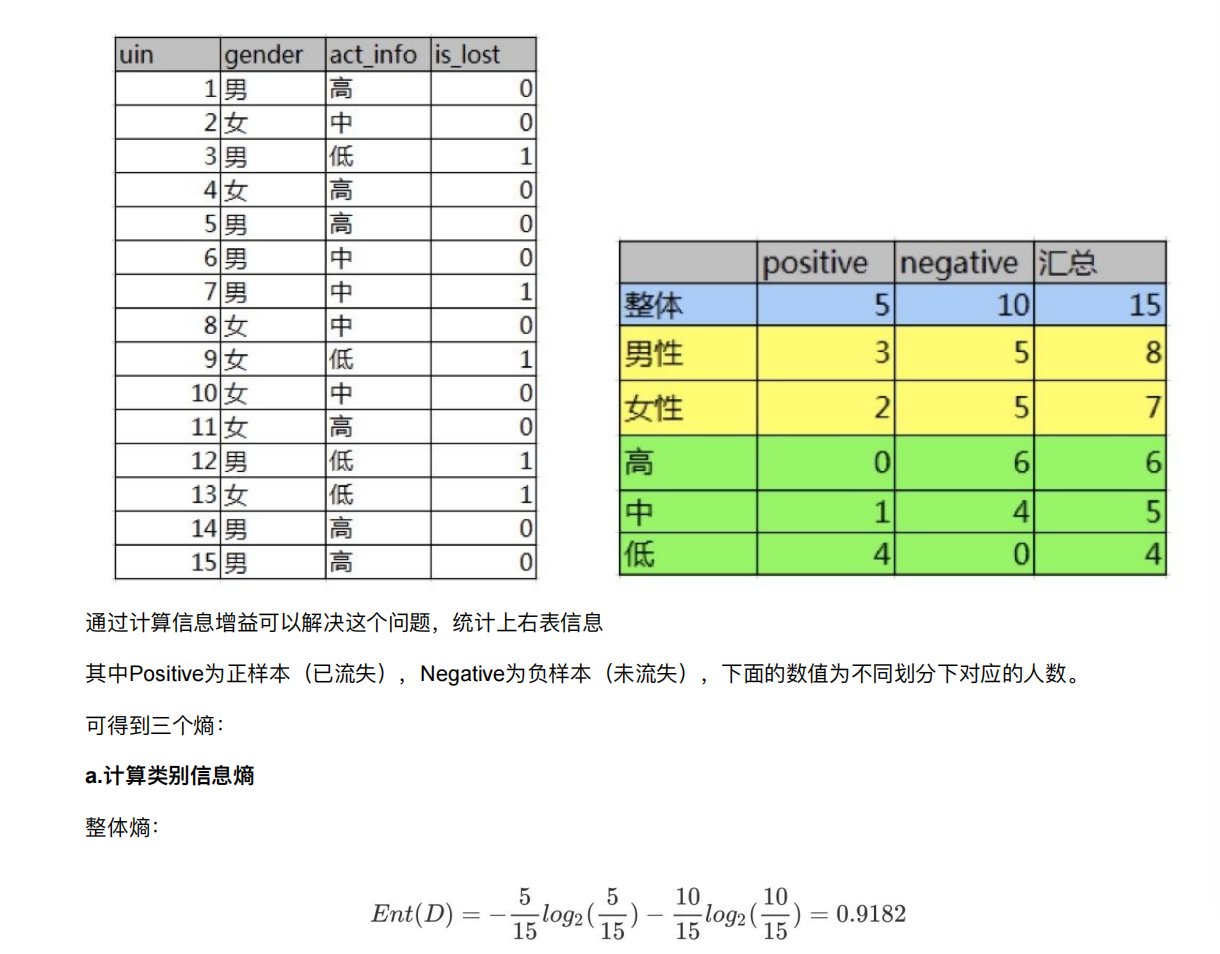
8.3 决策树的划分依据⼆----信息增益率

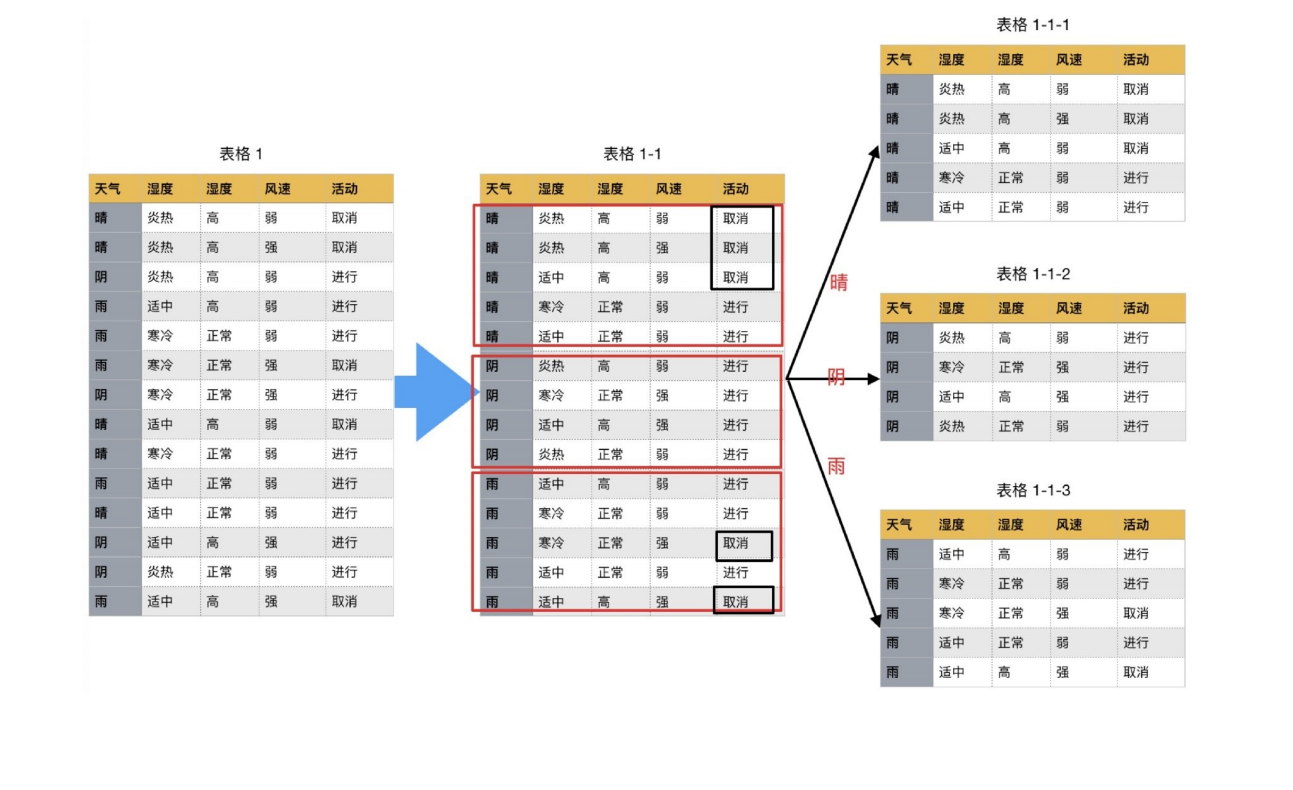
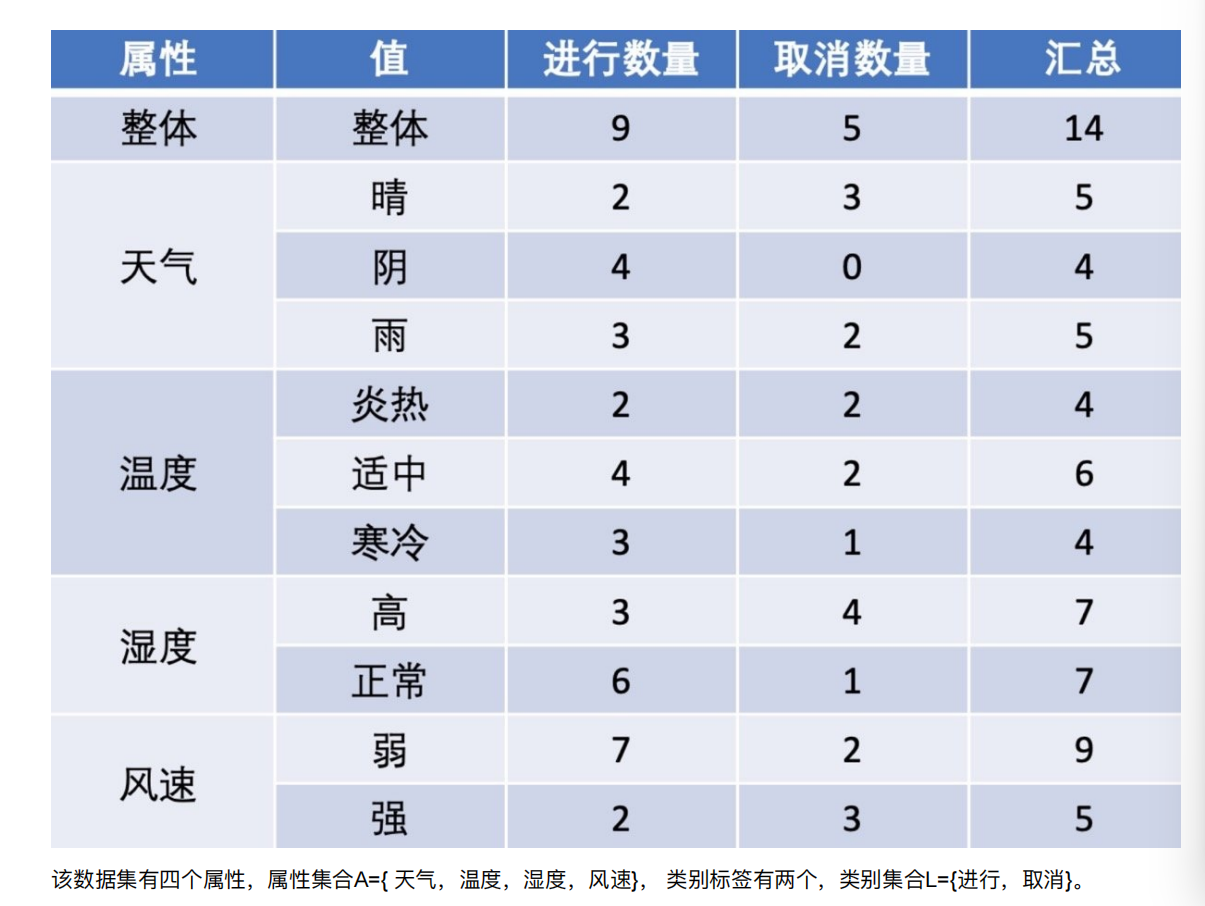
就是找出影响活动的首选因素

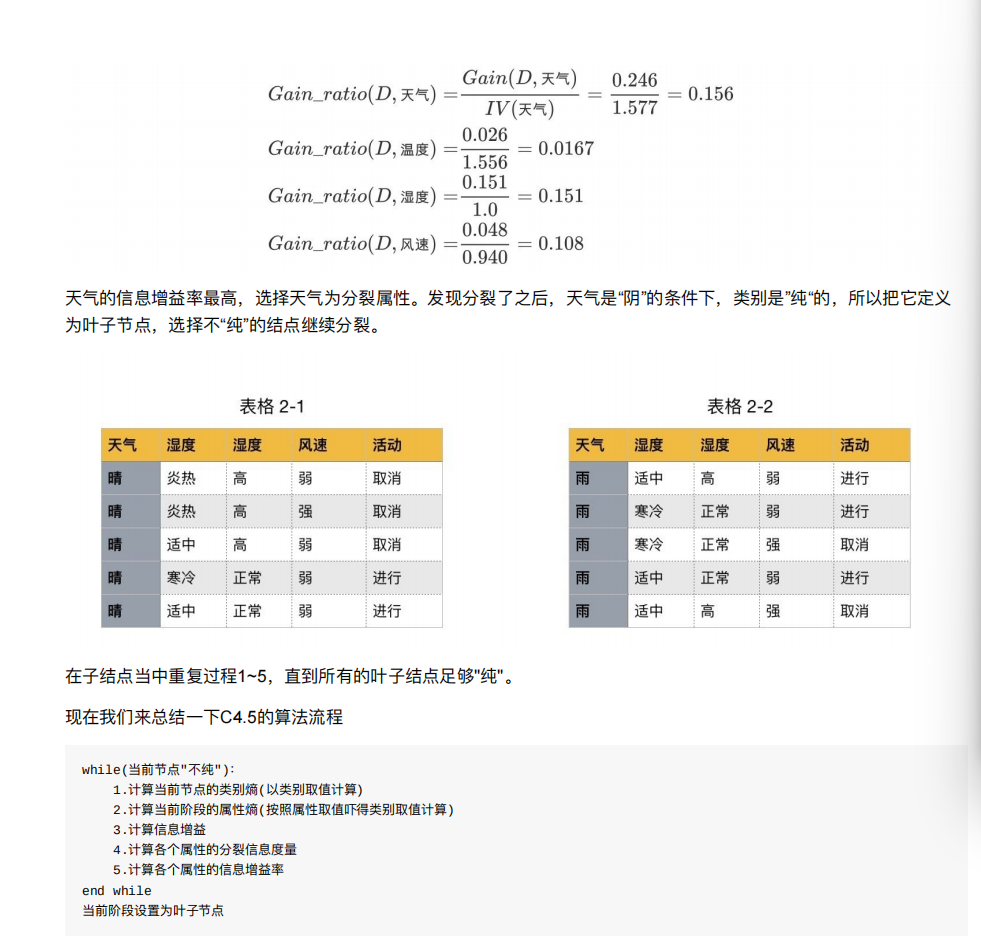
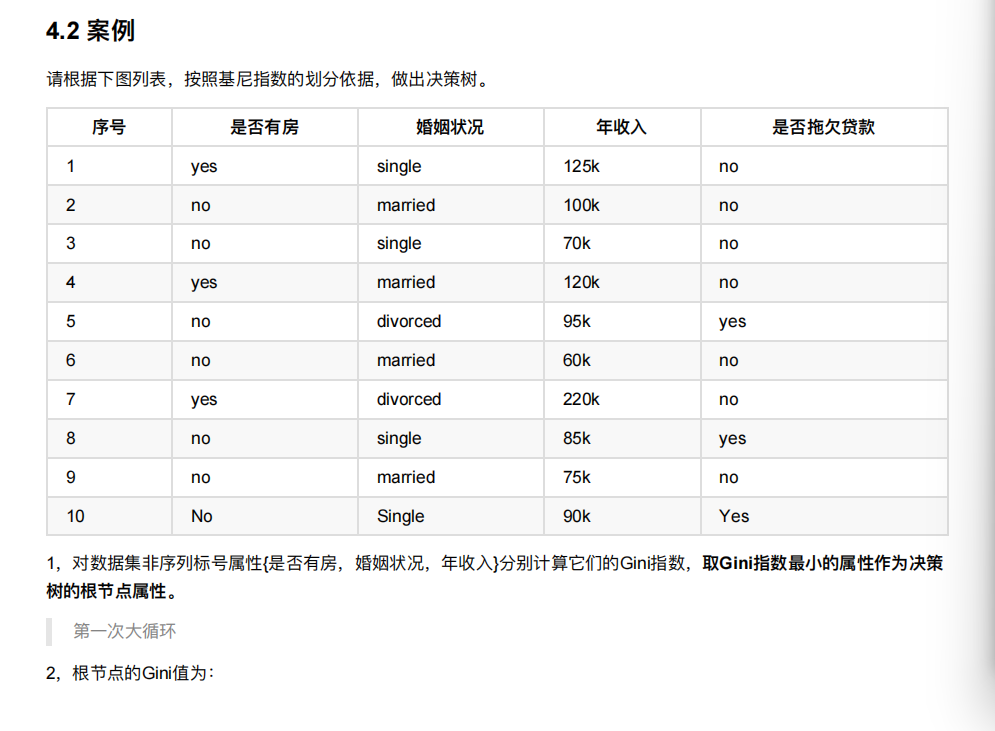
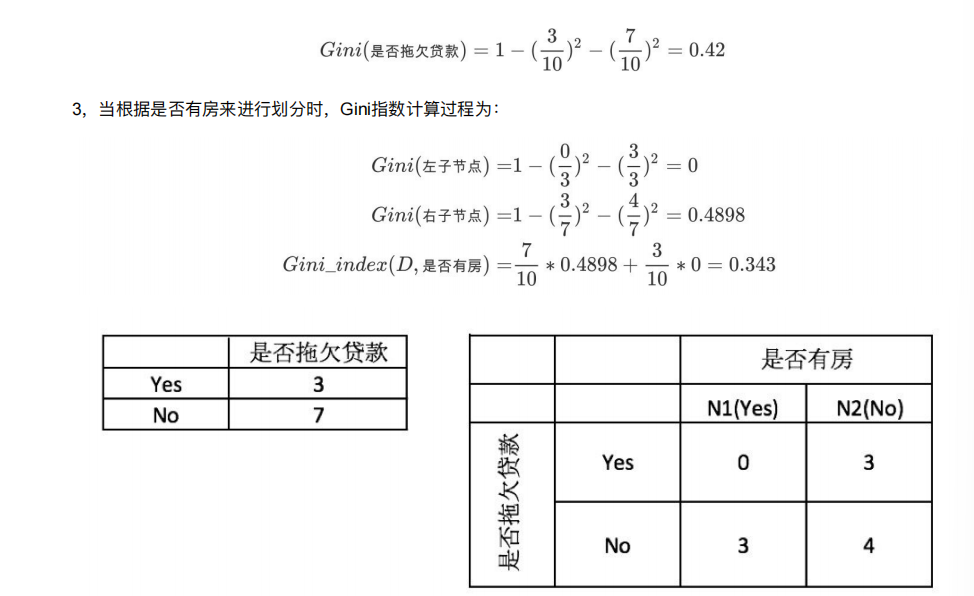
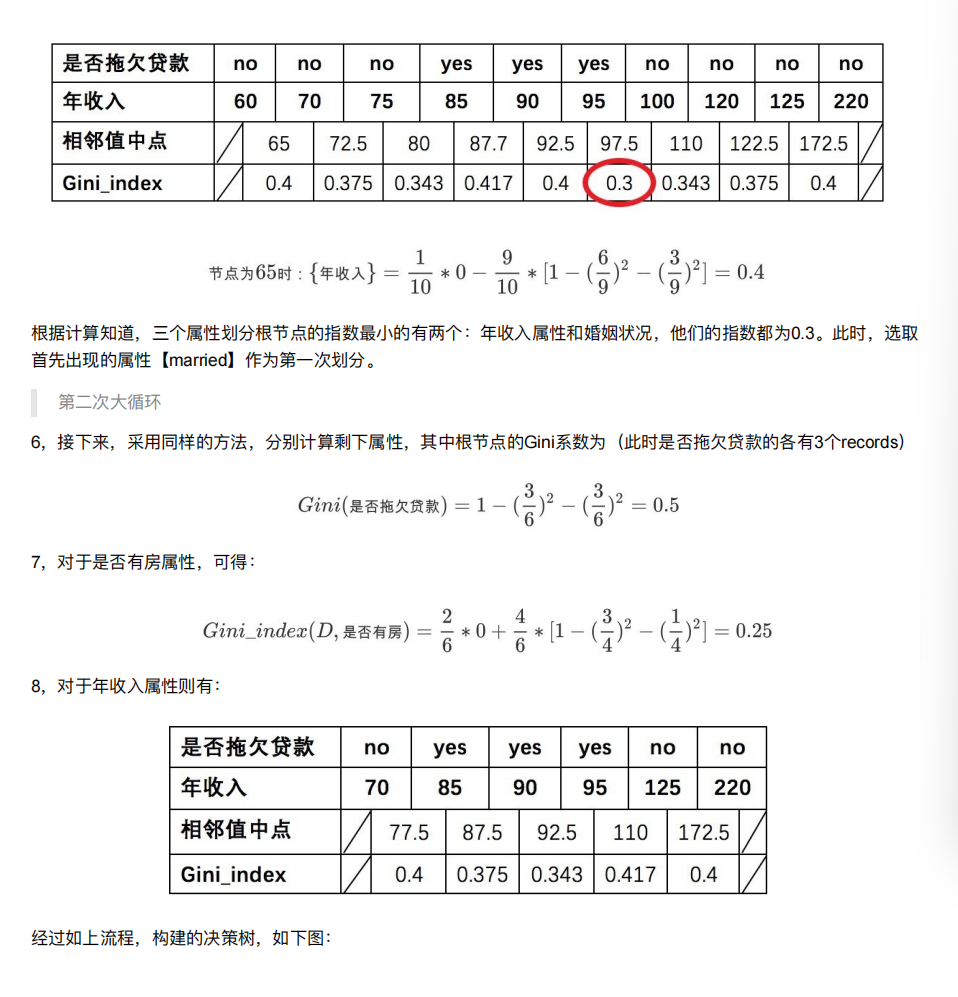
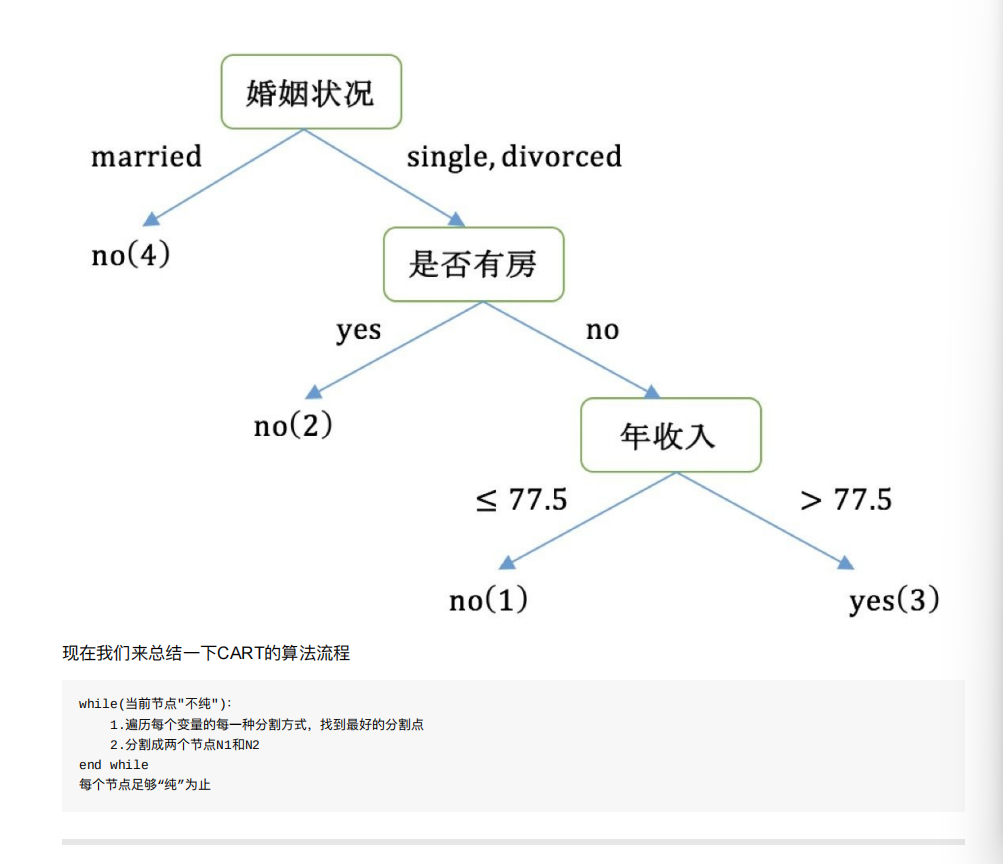
8.4 决策树的划分依据三 ----基尼值和基尼指数

总结