当前位置：首页 > news >正文

从浅入深：自编码器(AE)与变分自编码器(VAE)的核心原理与Pytorch代码讲解

news 2025/9/21 6:20:01

背景：为什么需要VAE？

在深度学习中，我们经常需要生成数据，例如：

生成类似真实人脸的图片

生成逼真的语音

从数据中学到潜在的低维表示（降维）

早期的方法，普通Autoencoder（自编码器）：

它把数据压缩到一个低维的“隐空间”再解码回来，学习到一个确定性映射。

核心思想：自我压缩与解压

例如：我给你一本很厚的书，要求你用一张小纸条写下这本书的核心内容，然后我把书拿走，让你只看这张小札条，再把整本书的内容复述出来。

这个过程听起来很难，为了能成功复述，你写在纸条上的必须是这本书最精髓、最具代表性的信息。你不能只是摘抄第一页，而是要真正“理解”了整本书，并将其压缩成精华。

自编码器做的就是类似的事情。它是一个无监督学习的神经网络模型，其基本目标非常简单：输入什么，就输出什么。也就是说，它试图学习一个恒等函数 f(x)=x。

你可能会问，这有什么意义呢？如果只是复制输入，那也太简单了。

这里的巧妙之处在于模型的结构设计。

自编码器的两大核心组件：

一个标准的自编码器由两部分组成：

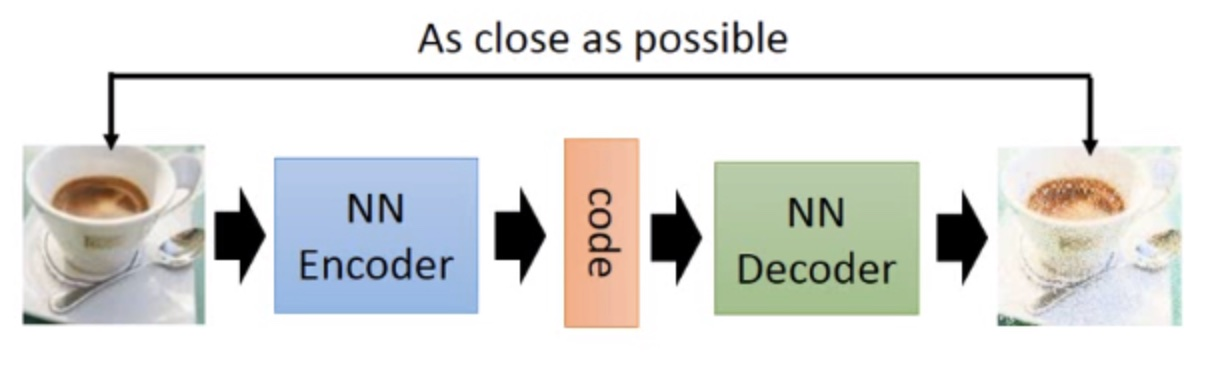
1.编码器 (Encoder)：它的任务就像我们前面提到的“阅读并总结”。它接收原始的、高维度的数据（比如一张图片的所有像素），然后把它“压缩”成一个维度低得多的潜在表示 (Latent Representation)。这个压缩后的信息通常被称为“编码”或“瓶颈特征 (Bottleneck)”。我们可以把这个过程表示为 z=encoder(x)，其中 x 是输入，z 是压缩后的编码。

2.解码器 (Decoder)：它的任务则是“根据总结复述全书”。它接收编码器产生的低维度编码 z，并尽力将其“解压”或者说“重建”为原始的高维度数据。这个过程可以表示为 x′=decoder(z)，其中 x′ 是重建后的输出。

整个模型的结构就像一个沙漏，从宽（输入层）到窄（瓶颈层），再到宽（输出层）。

输入数据 (x) → 编码器 → 潜在表示 (z) → 解码器 → 重建数据 (x')

学习的目标：

自编码器的训练目标是让重建数据 x′ 与原始输入数据 x 之间的差异尽可能小。我们用一个损失函数 (Loss Function)，也叫重构误差 (Reconstruction Error)，来衡量这个差异。例如，对于图像数据，我们通常使用均方误差 (Mean Squared Error)。模型会通过反向传播算法，不断调整编码器和解码器的参数，来最小化这个损失 L(x,x′)。

现在，我们回到那个关键问题：这为什么有用？

由于瓶颈层的维度远低于输入层，模型不可能简单地将输入数据“死记硬背”过去。为了能够成功地重建原始数据，编码器必须学会忽略数据中的噪声和不重要的细节，提取出数据中最核心、最本质的特征。

换句话说，自编码器被迫去“理解”数据，并学习到一个高效、紧凑的数据表示 z。这个副产品——也就是编码器本身以及它学到的潜在表示 z——往往比重建任务本身更有价值。

AE代码讲解：

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader# 定义自编码器网络结构
class Autoencoder(nn.Module):def __init__(self):super(Autoencoder, self).__init__()# 编码器：将输入压缩到低维表示self.encoder = nn.Sequential(nn.Linear(784, 256),  # MNIST图像展平后为784维nn.ReLU(),nn.Linear(256, 64),nn.ReLU(),nn.Linear(64, 16)    # 压缩到16维特征)# 解码器：从低维表示重建原始输入self.decoder = nn.Sequential(nn.Linear(16, 64),nn.ReLU(),nn.Linear(64, 256),nn.ReLU(),nn.Linear(256, 784),nn.Sigmoid()  # 输出值在0-1之间，与输入归一化范围匹配)def forward(self, x):encoded = self.encoder(x)decoded = self.decoder(encoded)return decoded# 准备MNIST数据集
transform = transforms.Compose([transforms.ToTensor(),  # 转换为张量transforms.Normalize((0.5,), (0.5,))  # 归一化到[-1,1]
])train_dataset = torchvision.datasets.MNIST(root='./data', train=True,download=True,transform=transform
)train_loader = DataLoader(train_dataset,batch_size=128,shuffle=True
)# 初始化模型、损失函数和优化器
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = Autoencoder().to(device)
criterion = nn.MSELoss()  # 使用均方误差作为重建损失
optimizer = optim.Adam(model.parameters(), lr=0.001)# 训练循环
num_epochs = 10
for epoch in range(num_epochs):for data in train_loader:img, _ = data  # 忽略标签img = img.view(img.size(0), -1).to(device)  # 展平图像 [128, 784]# 前向传播output = model(img)loss = criterion(output, img)# 反向传播和优化optimizer.zero_grad()loss.backward()optimizer.step()# 打印每个epoch的损失print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')print("训练完成！")# 测试重建效果（示例）
test_img, _ = next(iter(train_loader))
test_img = test_img[0].view(1, -1).to(device)
with torch.no_grad():reconstructed = model(test_img)# 可视化对比原始图像和重建图像（需要matplotlib）
# import matplotlib.pyplot as plt
# original_img = test_img.view(28, 28).cpu().numpy()
# reconstructed_img = reconstructed.view(28, 28).cpu().numpy()
# plt.subplot(1, 2, 1)
# plt.imshow(original_img, cmap='gray')
# plt.title('Original')
# plt.subplot(1, 2, 2)
# plt.imshow(reconstructed_img, cmap='gray')
# plt.title('Reconstructed')
# plt.show()

编码器：784 → 256 → 64 → 16（瓶颈层）

解码器：16 → 64 → 256 → 784（重建层）

使用ReLU激活函数（输出层用Sigmoid确保输出值在0-1之间）

MNIST图像被展平为784维向量

像素值归一化到[-1, 1]后，通过Sigmoid输出到[0,1]

使用均方误差（MSE）作为重建损失

Adam优化器学习率设为0.001

批量大小128，训练10个epoch

但是普通自编码器不会告诉我们：

1.隐空间的分布是什么样的

2.如何从“随机点”生成新的样本

普通AE只能重构已有数据，不能真正“生成”全新数据。

它的编码器将输入 x 映射到潜在空间中的一个确定的、唯一的点 z。如果你输入同一张猫的图片100次，你会得到100次完全相同的编码向量 z。

这个潜在空间可能是不连续的，充满了“空洞”。也就是说，在两个编码点之间随意取一个点，解码器可能无法生成任何有意义的东西，因为它在训练时从未见过那片区域。因此AE多用于数据的压缩和恢复，用于数据生成时效果并不理想。

为了解决这个问题，就有了 VAE。

VAE 不仅要学会压缩数据，还要学会“生成分布”，从而可以随机采样并生成全新的数据。

它的编码器输出的不是一个点，而是一个概率分布。

通常是一个高斯分布，由均值向量 μ 和标准差向量 σ 来定义。实际的编码 z 是从这个分布 N(μ,σ2) 中随机采样得到的。这意味着，你输入同一张猫的图片100次，会得到100个略有不同但都围绕着均值 μ 的编码向量 z。这种设计，加上一个特殊的损失项，强制让潜在空间变得连续、平滑。

变分自编码器VAE讲解：

VAE的结构和普通自编码器很像，但有关键区别：

输入x → 编码器(Encoder) → 隐变量z → 解码器(Decoder) → 输出x'

输入 x：真实数据，比如一张图片。

编码器 q(z|x)：把输入x映射到隐空间的分布，而不是一个点。

输出均值 μ(x) 和 方差 σ²(x)。

表示：给定x，隐变量z服从 N(μ(x), σ²(x))。

这意味着编码器认为：“对于这个输入 x，它在潜在空间中的表示应该在以 μ 为中心、以 σ 为标准差的这个范围内。” 它给出了一个模糊的“区域”，而不是一个精确的“坐标”。

我们现在有了一个分布，下一步就是从这个分布中采样一个点 z 出来，送给解码器。但这里有个大问题：“随机采样”这个动作是不可微分的，这意味着我们无法用梯度下降来训练网络。

为了解决这个问题，VAE 的提出者们想出了一个非常聪明的数学技巧——重新参数化技巧。

它把采样过程变成了：z=μ+σ⋅ϵ：

μ 和 σ 是编码器网络计算出的确定性数值。

ϵ 是一个从标准的正态分布 N(0,1)（均值为0，标准差为1）中随机采样的噪声。

你看，通过这个变换，网络的输出（μ 和 σ）与随机性（ϵ）被分开了。梯度可以顺利地流过 μ 和 σ 进行学习，而随机性则作为一个外部输入注入。这个小小的技巧是让 VAE 能够被成功训练的关键。

采样 z：从这个高斯分布中随机采样一个z。

解码器 p(x|z)：把z解码成一个重建的样本x'。

目标：让x'尽可能接近x，同时让隐变量z的分布接近一个标准正态分布 N(0,1)。

VAE数学核心（直观理解）：

VAE的数学核心是 概率图模型：

我们认为数据x是由一个潜在变量z生成的：

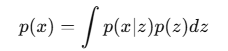
但直接计算这个积分非常难，潜在变量 z 虽然维度比原始数据 x 低，但它依然是一个高维向量（比如32维、64维甚至更高）。

现在，请你想象在一个100维的空间里做积分。这个空间的“体积”大到超乎想象，这就是所谓的“维度灾难” (Curse of Dimensionality)。

更糟糕的是，对于一个给定的数据 x，能够生成它的那些“有效”的 z 可能只分布在这个浩瀚空间里一个极其微小的区域内。

用数值方法（比如蒙特卡洛采样）去计算这个积分，就像是开着飞机在整个太平洋上空随机撒网，希望能捕到一条特定的鱼。

绝大多数的采样点 z 会落在 p(x∣z) 几乎为零的区域，对积分的贡献微乎其微，导致计算效率极低且结果不准确。

在 VAE 这样的模型里，p(x∣z) 是由一个深度神经网络（解码器）定义的。这是一个非常复杂、高度非线性的函数。我们根本无法得到这个积分的解析解 (analytical solution)，也就是一个封闭形式的数学公式。

所以我们引入一个近似分布 q(z|x) 去估计真实的后验 p(z|x)。

这里可能大家会比较模糊，我展开讲解一下：

我们假设存在一个潜在变量 z，它决定了数据 x的生成过程。

p(z)：隐变量的先验分布（通常是标准正态 N(0,1)）

p(x∣z)：给定 z，生成数据 x的条件分布（由解码器输出）

理论上，一张图片 x的真实概率可以写成：

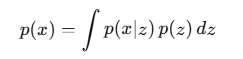
为什么我们要最大化数据似然 $\log p(x)$ ？

我们有一个真实数据集 {x1,x2,… }

我们希望模型学到的分布 p(x) 能够尽可能贴近真实数据的分布。

最大化 log⁡p(x)= 让“模型生成真实数据的概率”尽可能大

为什么需要近似分布 q(z∣x)？

上面讲了，P(X|Z)几乎无法直接计算出来。

我们引入一个可控的近似分布：

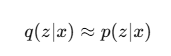
通过优化 q(z|x)，我们尽可能让它逼近真实后验 p(z∣x)。
这就是变分的含义：用一个“可优化的分布”去近似一个不可计算的分布。

最大化数据的似然：

变分下界（ELBO）：
通过数学推导，可以得到：

第一项：重构项：让生成的x'尽量接近真实x。

第二项：KL散度项：让编码器的隐空间分布q(z|x)接近先验分布p(z)（通常是标准正态N(0,1)）。

训练流程与代码讲解：

第1步：输入数据

我们从训练数据集中随机抽取一小批 (a mini-batch) 真实的样本数据，我们称之为 x。比如，128张人脸图片。

第2步：通过编码器 (Encoder)

我们将这批数据 x 输入到编码器网络 qϕ(z∣x) 中。编码器进行一次前向传播，它的输出不是一个直接的编码 z，而是我们之前学过的，用来描述潜在空间中概率分布的两个参数：

1.均值向量 μ

2.对数方差向量 log(σ^2)

提示：在实际代码中，网络通常输出对数方差 log(σ^2) 而不是标准差 σ 本身。

这样做是为了保证方差 σ^2 永远是正数（因为任何数的平方都是正的，而 log(σ^2) 的取值范围是整个实数域，更便于网络学习），并且能增加训练的数值稳定性。

第3步：采样潜在向量 z (重新参数化技巧)

这是 VAE 的核心。我们不能直接从编码器定义的分布 N(μ,σ2) 中“硬”采样，因为那样梯度无法回传。所以我们使用重新参数化技巧：

首先，从一个标准正态分布 N(0,I) 中生成一个与 z 维度相同的随机噪声向量 ϵ。

然后，计算出潜在向量 z： z=μ+σ⋅ϵ (这里的 σ 可以通过 σ=exp(0.5⋅log(σ……2)) 计算得到)

我再次提醒一遍，这个重参数化非常重要！直接从 $N(\mu,\sigma^2)$ 采样，z 对 μ、σ 没有显式可微关系，梯度无法回传；
重参数化把采样拆成“可微的线性变换 + 独立噪声”，从而让编码器参数可以被训练。

这样，我们就得到了一个既带有随机性、又与输入 x 相关（通过 μ 和 σ）的潜在编码 z。

第4步：通过解码器 (Decoder)

我们将刚刚采样得到的潜在向量 z 输入到解码器网络 pθ(x∣z) 中。解码器也进行一次前向传播，尽力将这个“压缩的精华” z 重建回原始数据的样子。它的输出是重建后的数据 x′。

第5步：计算总损失 (Total Loss)

现在我们手上有了所有需要的东西：原始输入 x，重建输出 x′，以及编码器产生的分布参数 μ 和 σ。我们可以计算 VAE 的总损失了，它由两部分组成：

重构损失 (Reconstruction Loss):

这个损失用来衡量原始输入 x 和重建输出 x′ 之间的差距。
如果输入是像 MNIST 那样的二值化图片，通常使用二元交叉熵 (Binary Cross-Entropy)。
如果输入是普通的彩色图片或者连续数值，通常使用均方误差 (Mean Squared Error, MSE)。
这个损失项会“逼迫”解码器学习如何生成逼真的图像，同时“逼迫”编码器提供足够有用的信息给解码器。

KL 散度损失 (KL Divergence Loss):

这个损失项像一个正则化器，它“规整”了潜在空间的结构，防止编码器为每个输入都分配一个相隔很远的“私人编码区”，从而使得整个潜在空间变得连续平滑。

总损失 = 重构损失 + KL 散度损失 （在实际应用中，KL散度项有时会乘上一个权重系数 β，即 β-VAE，用来调节它的影响力）

代码：

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
import numpy as np# 定义变分自编码器（VAE）模型
class VAE(nn.Module):def __init__(self, input_dim=784, hidden_dim=400, latent_dim=20):super(VAE, self).__init__()# 编码器部分self.encoder = nn.Sequential(nn.Linear(input_dim, hidden_dim),nn.ReLU(),nn.Linear(hidden_dim, hidden_dim),nn.ReLU())# 均值层self.fc_mu = nn.Linear(hidden_dim, latent_dim)# 对数方差层（使用对数方差确保方差为正）self.fc_logvar = nn.Linear(hidden_dim, latent_dim)# 解码器部分self.decoder = nn.Sequential(nn.Linear(latent_dim, hidden_dim),nn.ReLU(),nn.Linear(hidden_dim, hidden_dim),nn.ReLU(),nn.Linear(hidden_dim, input_dim),nn.Sigmoid()  # 输出值在0-1之间)def reparameterize(self, mu, logvar):"""重参数化技巧：从潜在空间采样"""std = torch.exp(0.5 * logvar)  # 计算标准差eps = torch.randn_like(std)    # 从标准正态分布采样return mu + eps * std          # 返回采样结果def forward(self, x):# 编码过程h = self.encoder(x)mu = self.fc_mu(h)logvar = self.fc_logvar(h)# 重参数化采样z = self.reparameterize(mu, logvar)# 解码重建x_recon = self.decoder(z)return x_recon, mu, logvar# 定义VAE损失函数（重建损失 + KL散度）
def vae_loss(recon_x, x, mu, logvar):# 重建损失（二元交叉熵或均方误差）BCE = nn.functional.binary_cross_entropy(recon_x, x, reduction='sum')# KL散度（衡量潜在分布与标准正态分布的差异）KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())return BCE + KLD# 准备MNIST数据集
transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.5,), (0.5,))  # 归一化到[-1,1]
])train_dataset = torchvision.datasets.MNIST(root='./data', train=True,download=True,transform=transform
)train_loader = DataLoader(train_dataset,batch_size=128,shuffle=True
)# 初始化模型、优化器
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = VAE().to(device)
optimizer = optim.Adam(model.parameters(), lr=1e-3)# 训练循环
num_epochs = 20
for epoch in range(num_epochs):total_loss = 0for batch_idx, (data, _) in enumerate(train_loader):data = data.view(data.size(0), -1).to(device)  # 展平图像# 前向传播recon_batch, mu, logvar = model(data)# 计算损失loss = vae_loss(recon_batch, data, mu, logvar)# 反向传播和优化optimizer.zero_grad()loss.backward()optimizer.step()total_loss += loss.item()# 打印每个epoch的平均损失avg_loss = total_loss / len(train_loader.dataset)print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {avg_loss:.4f}')print("训练完成！")# 可视化重建结果
def visualize_reconstruction():model.eval()with torch.no_grad():# 获取一批测试数据test_loader = DataLoader(train_dataset, batch_size=5, shuffle=True)data, _ = next(iter(test_loader))data = data.view(data.size(0), -1).to(device)# 重建图像recon, _, _ = model(data)# 转换为numpy数组用于绘图data = data.cpu().numpy()recon = recon.cpu().numpy()# 绘制原始图像和重建图像fig, axes = plt.subplots(2, 5, figsize=(10, 4))for i in range(5):axes[0, i].imshow(data[i].reshape(28, 28), cmap='gray')axes[0, i].axis('off')axes[1, i].imshow(recon[i].reshape(28, 28), cmap='gray')axes[1, i].axis('off')plt.show()# 可视化潜在空间
def visualize_latent_space():model.eval()with torch.no_grad():# 获取一批数据及其标签test_loader = DataLoader(train_dataset, batch_size=1000, shuffle=True)data, labels = next(iter(test_loader))data = data.view(data.size(0), -1).to(device)# 获取潜在表示h = model.encoder(data)mu = model.fc_mu(h)# 转换为numpy数组mu = mu.cpu().numpy()# 绘制潜在空间plt.figure(figsize=(10, 8))plt.scatter(mu[:, 0], mu[:, 1], c=labels, cmap='tab10', alpha=0.7)plt.colorbar()plt.title('VAE Latent Space')plt.xlabel('z-dim 1')plt.ylabel('z-dim 2')plt.show()# 生成新样本
def generate_samples():model.eval()with torch.no_grad():# 从标准正态分布采样z = torch.randn(64, 20).to(device)# 通过解码器生成样本samples = model.decoder(z).cpu()# 绘制生成样本fig, axes = plt.subplots(8, 8, figsize=(10, 10))for i, ax in enumerate(axes.flatten()):ax.imshow(samples[i].view(28, 28), cmap='gray')ax.axis('off')plt.show()# 执行可视化
visualize_reconstruction()
visualize_latent_space()
generate_samples()

self.encoder: 编码器。它由一系列全连接层 (nn.Linear) 和 ReLU 激活函数组成。它的任务是将输入的 28×28=784 维的扁平化图像，一步步压缩，最后输出一个 hidden_dim（这里是400）维的特征向量。
self.fc_mu 和 self.fc_logvar: 这是 VAE 的关键。编码器提取的400维特征向量并不是直接的潜在编码 z。而是兵分两路，分别通过这两个独立的全连接层，生成潜在分布的两个参数：均值 μ 和对数方差 log(σ2)。它们的维度都是 latent_dim（这里是20）。
self.decoder: 解码器。它的结构与编码器大致相反，像一个镜像。它的任务是接收一个 latent_dim（20维）的潜在向量 z，然后一步步将其“放大”和“解码”，最终重建回 input_dim（784维）的图像。
nn.Sigmoid(): 解码器的最后一层使用了 Sigmoid 激活函数。这是为什么呢？ 因为 MNIST 图像的像素值经过 ToTensor() 处理后，范围在 [0,1] 之间。Sigmoid 函数的输出范围恰好也是 [0,1]，这使得重建出的图像像素值能与原始图像在同一尺度上进行比较，非常适合使用二元交叉熵损失函数。

class VAE(nn.Module):def __init__(self, input_dim=784, hidden_dim=400, latent_dim=20):...

input_dim=784：MNIST图片28x28 → 展平为784维
hidden_dim=400：隐藏层维度
latent_dim=20：潜在空间维度（z的维数）

self.encoder = nn.Sequential(nn.Linear(input_dim, hidden_dim),nn.ReLU(),nn.Linear(hidden_dim, hidden_dim),nn.ReLU()
)

输入784 → 两层全连接隐藏层（ReLU激活） → 输出隐藏特征h

self.fc_mu = nn.Linear(hidden_dim, latent_dim)
self.fc_logvar = nn.Linear(hidden_dim, latent_dim)

编码器输出隐藏特征h后，分别映射出均值 μ 和 对数方差 logσ²。
使用log方差是为了确保方差永远为正（exp后自动正数）。

self.decoder = nn.Sequential(nn.Linear(latent_dim, hidden_dim),nn.ReLU(),nn.Linear(hidden_dim, hidden_dim),nn.ReLU(),nn.Linear(hidden_dim, input_dim),nn.Sigmoid()
)

输入z（20维） → 两层隐藏层 → 输出784维图像
最后一层用Sigmoid让像素值范围在[0,1]。

重参数化技巧

def reparameterize(self, mu, logvar):std = torch.exp(0.5 * logvar)  # 标准差 σeps = torch.randn_like(std)    # 从 N(0,1) 采样return mu + eps * std          # z = μ + σ·ε

std = torch.exp(0.5 * logvar): 从对数方差 log(σ2) 计算出标准差 σ。

$\sigma = \sqrt{\sigma^2} = \sqrt{\exp(\log(\sigma^2))} = \exp(0.5 \cdot \log(\sigma^2))$

eps = torch.randn_like(std): 从标准正态分布（均值为0，方差为1）中采样一个噪声 ϵ，其形状与 std 完全相同。

return mu + eps * std: 实现了公式 z=μ+ϵ⋅σ。这样，梯度就可以通过 μ 和 σ 正常反向传播，而随机性则由 ϵ 引入。

def forward(self, x):h = self.encoder(x)mu = self.fc_mu(h)logvar = self.fc_logvar(h)z = self.reparameterize(mu, logvar)x_recon = self.decoder(z)return x_recon, mu, logvar

流程：

输入x（展平图像）
编码器 → 输出隐藏h
计算 μ 和 logσ²
重参数化采样 z
解码器重建 x'

损失函数

def vae_loss(recon_x, x, mu, logvar):BCE = nn.functional.binary_cross_entropy(recon_x, x, reduction='sum')KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())return BCE + KLD

VAE的目标 = 重建误差 + KL散度

BCE：重建误差
- 这里用二元交叉熵(Binary Cross Entropy)
- 衡量重建图像和原图的像素差
KLD：KL散度
- 衡量 q(z|x) 和 p(z)（标准正态）之间的差异
- 保证隐变量分布接近 N(0,1)，便于生成。

transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.5,), (0.5,))
])
train_dataset = torchvision.datasets.MNIST(root='./data', train=True, download=True, transform=transform
)
train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True)

MNIST：28×28灰度手写数字数据集
ToTensor：把图片转为[0,1]的张量
Normalize：标准化到[-1,1]（可加速训练）
DataLoader：每次取128张图，打乱顺序

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = VAE().to(device)
optimizer = optim.Adam(model.parameters(), lr=1e-3)
num_epochs = 20
for epoch in range(num_epochs):total_loss = 0for batch_idx, (data, _) in enumerate(train_loader):data = data.view(data.size(0), -1).to(device)  # 展平成784维recon_batch, mu, logvar = model(data)         # 前向传播loss = vae_loss(recon_batch, data, mu, logvar)# 损失optimizer.zero_grad()loss.backward()                               # 反向传播optimizer.step()                               # 更新参数total_loss += loss.item()avg_loss = total_loss / len(train_loader.dataset)print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {avg_loss:.4f}')

训练20轮：

每个Batch：
- 展平图像 → 前向计算 → 损失
- 清空梯度 → 反向传播 → 优化参数
打印每轮的平均损失

data = data.view(data.size(0), -1).to(device): 从 DataLoader 取出一批数据，并将其从 [128, 1, 28, 28] 的形状展平为 [128, 784]，以匹配我们全连接层的输入。

recon_batch, mu, logvar = model(data): 执行一次完整的前向传播。

loss = vae_loss(...): 计算总损失。

optimizer.zero_grad(): 梯度清零。PyTorch 的梯度是累加的，所以在每次反向传播前必须手动清零。

loss.backward(): 反向传播。计算损失函数关于模型所有参数的梯度。

optimizer.step(): 参数更新。优化器根据刚刚计算出的梯度，对模型参数进行一次更新。

输入图像 x↓ Encoder
输出 μ, logσ²↓ Reparameterization
采样 z = μ + σ·ε↓ Decoder
重建图像 x'↓ Loss
BCE(x,x') + KL(q(z|x)||N(0,1))

可视化函数：

这部分用于评估我们训练好的模型。

model.eval(): 将模型切换到评估模式。这会关闭一些只在训练时使用的层，如 Dropout。
with torch.no_grad(): 在这个代码块中，禁用梯度计算。这会节省内存并加速计算，因为在评估时我们不需要更新模型。
visualize_reconstruction(): 展示模型重建图像的能力。
visualize_latent_space(): 将高维（20维）的潜在空间中的前两维 (mu[:, 0], mu[:, 1]) 绘制出来，并用颜色表示数字的类别。我们可以观察到，训练好的 VAE 会将相同类别的数字在潜在空间中聚集在一起。
generate_samples(): 展示模型的生成能力。我们从标准正态分布中随机采样一些点 z，然后只通过解码器，就能生成全新的、从未在数据集中出现过的数字图像。