数据结构与算法3：链式最基本的表示和实现——单链表

标题 2.5-I、链式最基本的表示和实现——单链表

2.5.1、知识回顾以及引入链式:

顺序表的特点：以物理位置相邻表示逻辑关系。
顺序表的优点：任一元素均可随机存取。
顺序表的缺点：进行插入和删除操作时，需移动大量的元素。存储空间不灵活。
由于顺序表固有的缺点，存储空间不灵活，存储多了浪费，少了又容易溢出，为了解决该问题，链式存储结构应用而生，如下：
链式存储结构：
● 结点字存储器中的位置时任意的，及逻辑上相邻的数据元素在物理上不一定相邻。
线性表的链式表示又称为非顺序映像或链式映像。
那怎么存储的呢？
● 用一组物理位置任意的存储单元来存放线性表的数据元素。
● 这组存储单元即可以是连续的，也可以是不连续的，甚至是零散分布在内存中的任意位置上的。
● 链表中元素的逻辑次序和物理次序不一定相同。

2.5.2、两个经典案例

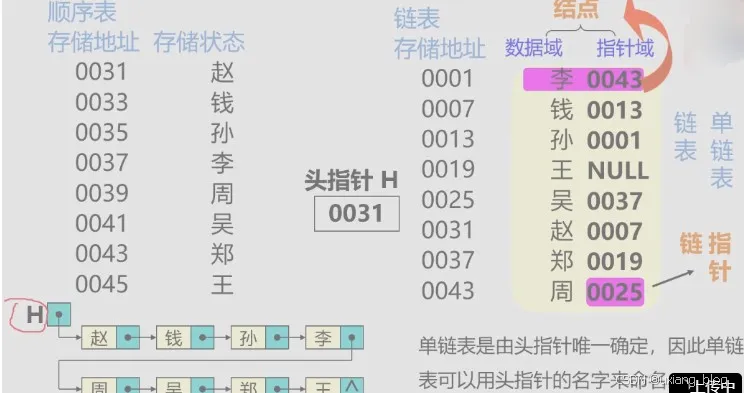
例如：线性表：(赵、钱、孙、李、周、吴、郑、王)

例如：26个英文小写字母表的链式存储结构

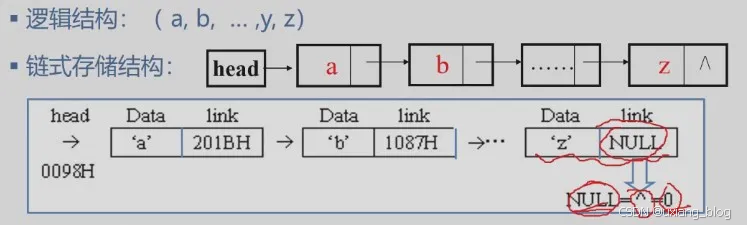
各结点由两个域组成：
● 数据域：存储元素数值数据
● 指针域：存储直接后继结点的位置

2.5.3、与链式存储有关的术语和示意图

1、结点：数据元素的存储映像。由数据域和指针两部分组成
数据域+ 指针域名
2、链表：n个结点由指针链组成一个链表。它是线性表的链式映像，称为线性表的链式存储结构。
示意图：

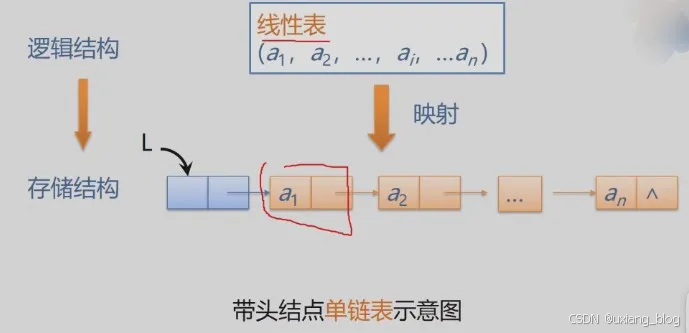
注解：^表示NULL的意思。

3、单链表、双链表和循环链表：

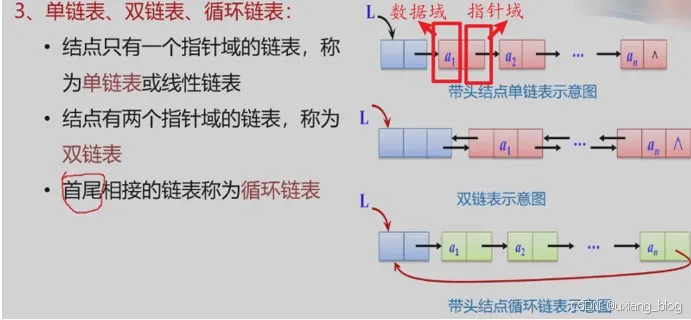
注解:单链表只有一个指针域，用来存储下一个元素的地址，双链表以数据域为中心，有一前一后两个指针域，前指针域用来存储前趋元素的地址，后指针域用来存储后继元素的地址。循环链表中是单链表的的改变，最后一个元素的指针域由原来的存储为NULL变为用来存储的是第一个元素的地址，使其首位相接，谓循环链表。

4、头指针、头结点和首结点：

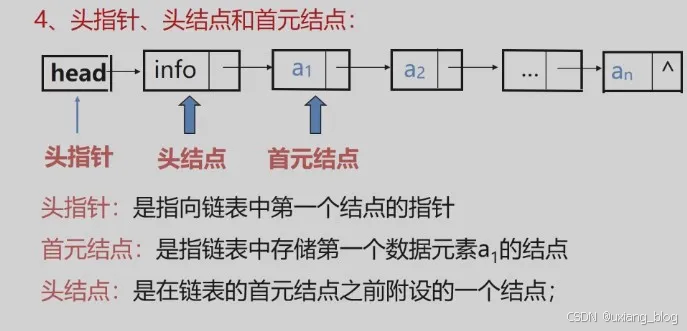
上面例子中的链表的存储结构示意图有以下两种形式：

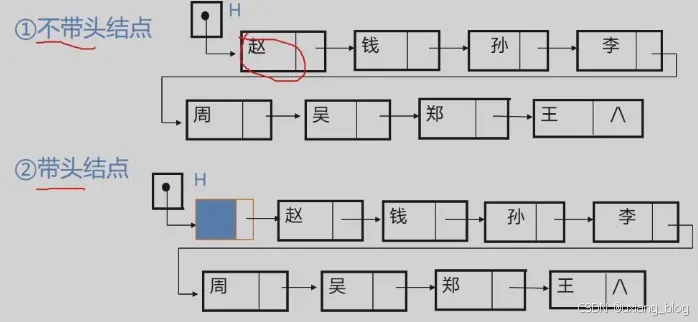
2.5.4、讨论

讨论1、如何表示空表？
● 无头结点时，头指针为空时表示空表
● 有头结点时，当头结点的指针域为空的时表示为空表

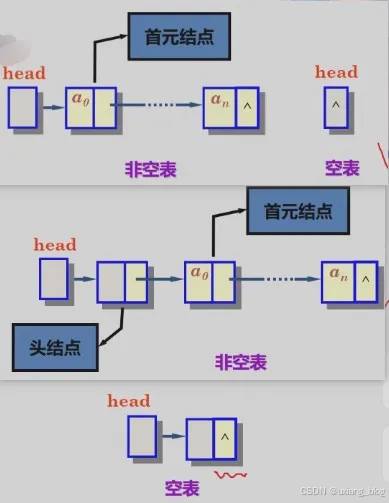
讨论2、在链表中设置头结点有什么好处？
● 1、便于首元结点的处理。首元姐结点的地址保存在头结点的指针域中，所以·在链表的第一个位置上的操作和其他位置一致，无须进行特殊处理；
● 2、便于空表的和非空表的统一处理。无论链表是否为空，头指针都是指向头结点的非空指针，因此空表和非空表的处理也就统一了。
讨论3：头结点的数据域内装的是什么？

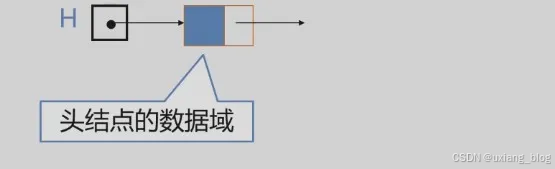
头结点的数据域可以为空，也可以存放线性表长度等附加信息，但此结点不能计入链表长度值。
链表的(链式存储结构)的特点
（1）、结点在存储器中的位置手机任意的，即逻辑上相邻的数据元素在物理上不一定相邻。
（2）、访问时只能通过头指针进入链表，并通过每个结点的指针域依次向后顺序扫描其余结点，所以寻找第一个结点和最后一个结点所花费的时间不等。——这种存取元素的方法叫做顺序存取法。

2.5.5、知识回顾

线性表的链式存储结构
● 线性表中数据元素（结点）在存储中的位置是任意的，即逻辑上相邻的数据元素在物理位置上不一定相邻。
● 结点

● 链表 n个结点由指针链组成一个链表。 链表是顺序存取的。
○ 单链表：每个结点只有一个指针域。
○ 双链表：每个结点有两个指针域
○ 循环链表：链表结点首尾相连。

2.5.6、单链表的定义和表示

带头指针的单链表：

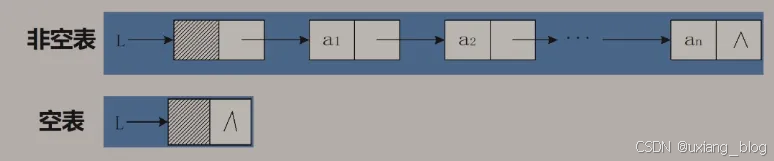
单链表是由表头唯一确定，因此单链表可以用头指针的名字来命名。若头指针名是L,则把链表称为表L。
单链表的存储结构

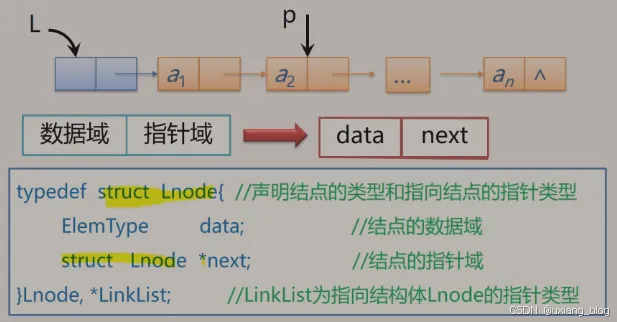
注解：这里的data类型统称为ElemType,具体是什么类型，是int还是float,都视具体情况确定。
struct Lnode用自己定义自己，这种属于嵌套类型的定义。struct Lnode（{}里面的）是什么样的类型呢？是指包括两个成员（ElemType data和struct Lnode next）的struct Lnode{}这种类型指针去。前面的typedef给这部分重新起了一个名字。
Lnode, LinkList;//Lnode,结点，比如图中a,对a结点操作就是a.
data,a.next。定义这种指向结点的指针类型可以用p（把LinkList具体化了）或者Lnode, *LinkList也可以用Lnode *L，LinkList L表示。

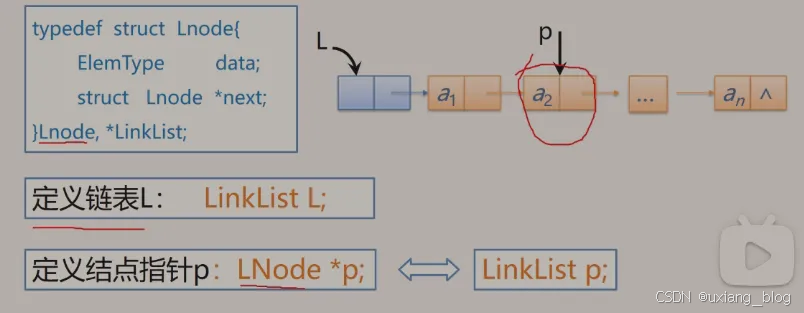
注解：要操作一个单链表L就用LinkList L；要定义一个指针变量，这个指针变量是指向某一个结点的，那就用LNode *p来表示，p本来就指针，所以也可以用 LinkList p;来表示。
通常来说，定义指向头结点的指针，它就代表整个列表，常用LinkList L;来定义，而不是用LNode *L；指向这个结点的指针，虽然也对，但是不建议这么定义。指向结点的指针呢？通常用LNode *p来表示，而不用LinkList p；

例如，存储学生学号、姓名、成绩的单链表结点类型定义如下：

注解：*next指针——>指向那种类型的变量？struct student next？——>指向具有这4个成员Struct student{ char num[8]; char name[8]; int score; struct student *next}这种类型。

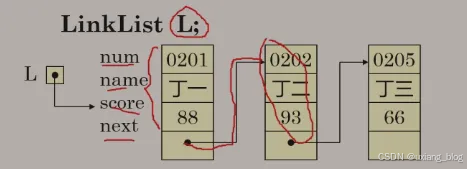
注解：首先它有三个数据域，存储num、和name、score，还有一个指针域，next,是那种类型的呢？指向后面（0202，丁二，93, .）它自己这种类型，然后定义一个指向这个表的指针，LinkList L，让L指向第一个元素。
但是这种方式不大常用，为了统一链表的操作，通常如下定义：
将数据项单独定义成一个结构类型ElemType，然后直接用这个结构类型直接定义一个数据域data，这样就和前面的操作统一了，就方便操作。

2.5.7、单链表基本操作的实现

2.5.7.1、【单链表的初始化（算法2.6）】（带头结点的单链表）

● 即构造一个如图的空表

算法步骤
● （1）生成新结点作头结点，用头指针L指向头结点。
● （2）将头结点的指针域置空。
算法描述

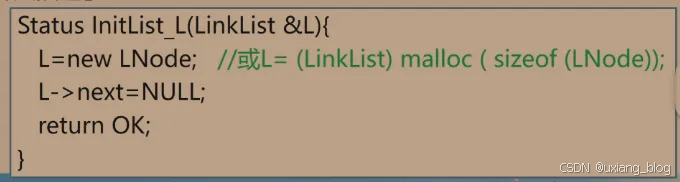
注解：C++：L = new LNode；//这句的含义是把new的结点的地址赋予给L。或C: L= (LinkListA)malloc (sizeof(LNode))；//此句的意思是，malloc()从内存中找到一个这么大空间sizeof(LNode),然后经过（LinkList）转换成指向结点的指针的空间的地址赋予给L。
L是一个指针变量，怎么操作它所指的结点的指针域呢？——。
L->next = NULL;//将L所指的结点的指针域置空。
ruturn OK;//返回OK结束。

2.5.7.2、【补充单链表的几个常用简单算法】

2.5.7.2.1、算法1：判断链表是否为空：

空表：链表中无元素，称为空链表(头指针和头结点仍然存在)
算法实现：判断头结点指针域是否为空

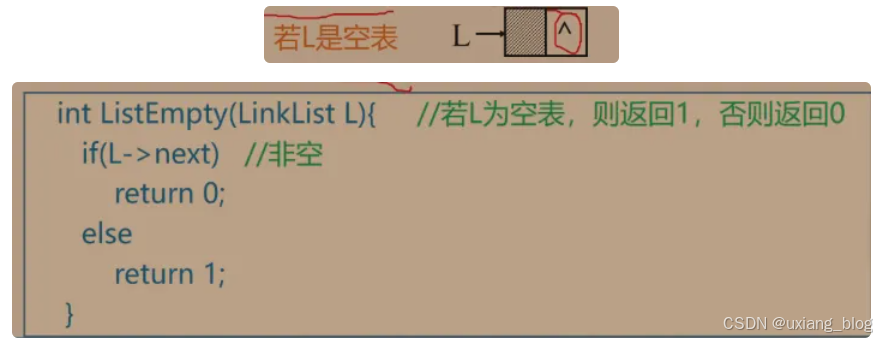
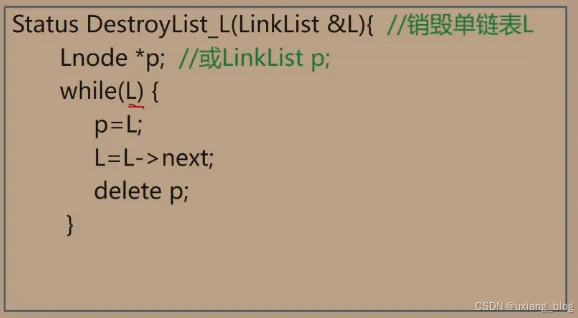
2.5.7.2.2、算法2：单链表的销毁：链表销毁后不存在。

算法步骤：从头指针开始，依此释放所有结点。

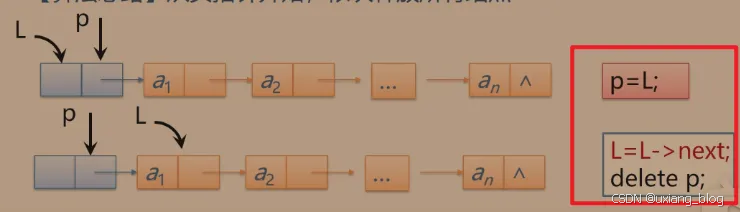
注解：怎么操作呢？还需要一个另为一个指针变量（如p），用来操作结点。操作指针变量p,将它指向头结点L,然后把结点L释放掉（也指删掉）。怎么把一个变量（这里具体化是指针变量p）指向头结点(此处具体化指头结点L)呢？我们把这个空间的（这里指的是头结点的空间）地址赋值给这个变量，比如p = &a；如此则有p=L；便代表指针变量p指向头结点L了，接着便可以把这个结点删掉了，但不能直接删掉，因为删掉之后下一个结点的地址也随之被删掉了，我们的办法是先将L移动到下一个结点的位置（由链表的性质，头结点是由数据域+指针域组成的，而头结点的指针域存放着后继结点的地址，所以可以利用头结点所存的地址移动到下一个结点，即L=L->next;），然后删除前一个结点，依此类推，就释放掉了整个单链表。释放的具体操作是，C++：delete p; C：free(p）。注意两组搭配：
● C++：new 对应删除 deletep；
● C: malloca()函数 对应删除 free§;
但是问题来了，依此类推下去什么时候结束呢？我们直到最后一个an的结点数据域中是^{,意思是空，所以见到这个标志（},NULL，空）则说明该结束了，即L = L->NULL 。结束条件：L == NULL，循环条件：L! = NULL，非空也可简单表示成：L
算法描述：

2.5.7.2.3、算法3：清空单链表

链表仍存在，但链表中无元素，成为空链表（头指针和头结点仍然在）
算法步骤：依此释放所有结点，并将头结点指针域设置为空。

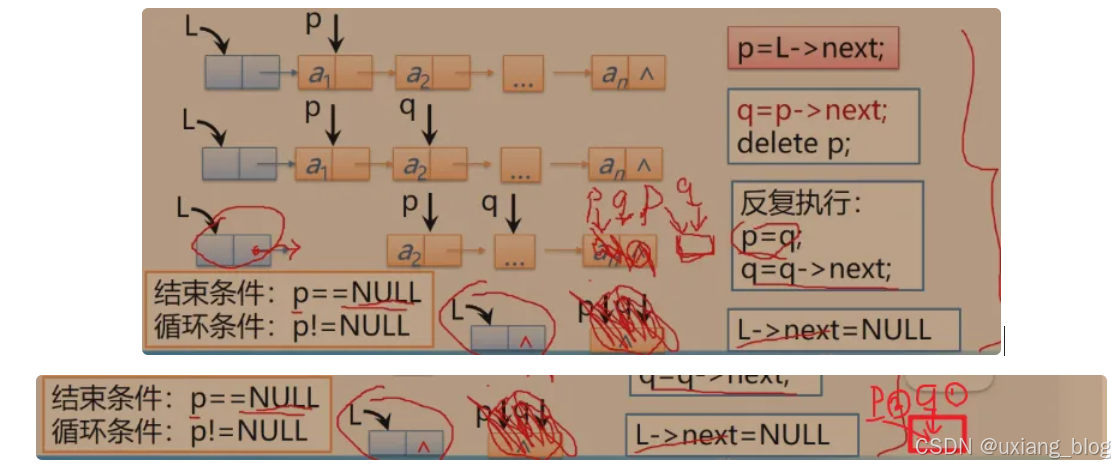
注解：比如现在有一个列表L,我们把链表清除，从第一个元素开始，依此清除，最后将头节点指针域置为空，就结束了。那我们说从头元结点开始，那怎么获取第一个结点的地址呢？第一个结点的地址在首元结点的next域（应该是指针域），L->next,获得即首元结点（存放第一个元素的结点）的地址，然后把它赋值给指针p，即L= L->next。上一次做销毁操作的是时候连头结点一块都销毁了，那我们怎么让指针指向头结点呢？头指针里面就存在头结点的地址，直接把头结点L赋值给p,即p=L。点单链表中最长用的操作，p= L->next (首元结点),和 p=L（头结点）是常用的操作。在清空链表时，是从清空首元结点开始的，并不像销毁单链表那样所有结点都删除，而且还有最后给头结点置空，所以清空链表中独有的操作是，有指针变量p来精进行操作（删除动作），另为一个变量q来记录下一结点的地址。先由q记录下一结点的地址q=p->next;然后用指针变量p删除前面一个结点，接着再由记录变量q告诉指针变量p接下来要删除哪一个结点，即p=q;，随后记录变量q便跳到下下个结点去记录q=q->next；依此往复，(如果p=q和q=q->next互换顺序，那么两个变量同时指向同一个结点，没法删除)。
那什么时候结束呢?将头结点的指针域设置为空就可以。

算法描述：

2.5.7.2.4、算法4：求单链表的表长

算法思路：从首元结点开始，依此计数所有结点

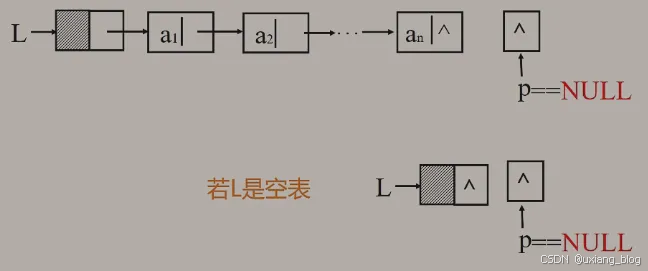
注解：现在我们数出单链表中有多少个元素。从首元结点开始，依此计数所有结点。怎么从首元结点开始呢？首元结点的地址存在于头结点的next域存着，则需要把头结点next域赋值给指针即可，即p = L -> next（i=1,ai）;然后看一下这个结点是不是空的，是空的就不再往下面数了。怎么解决从首元结点移动下一个结点的呢？根据单链表的性质，首元结点的next域是存着下一个结点的地址的，则选要把它的next域赋值给指针即可，p = p -> next；其他移动情况也是同理，直到指针为NULL为止。若是空表则需要使得指针p所指结点为空，则需要将头指针L赋值给p，即p = L。

算法实现：

2.5.8、单链表的基本操作的实现

知识回顾：（下图内容非常重要是需要记住的内容）

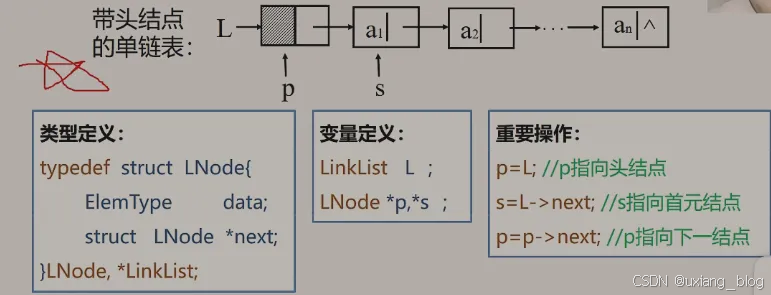
注解：
类型定义部分：链表当中每个结点需要存储数据元素，除了存储数据元素本身，还需要存储下一个元素的地址，所以它的结点类型是由两个成员变量，一个存储数据元素的data,和另一个存储地址next的指针，由这个两个成员变量组成的这种结构类型struct LNode{},然后同typedef 重新把它们定义成了结构类型名LNode和LinkList，一个是这种类型的结点LNode，另一个是指向这种结点的指针类型。
变量定义部分：那么我们就可以利用它们两个去定义我们需要的结点和指针。LinkList本身就是指针型，所以L前面无需加*号，指向结点的类型需要加✳号，*p,*s。
重要操作部分：
p=L;//p指向头结点
s= L ->next;//s指向首元结点
p=p -> next;//p指向下一个结点

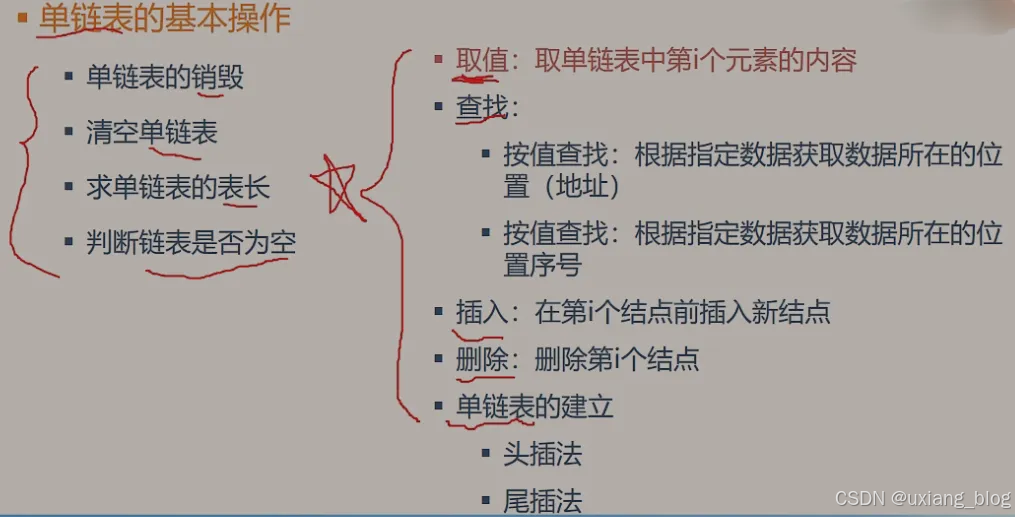
之前学习了单链表的基本操作：
● 单链表的销毁
● 清空单链表
● 求单链表的表长
● 判断链表是否为空
接下来要学习的是:——非常重要
● 取值：取单链表中第i个元素的内容
● 查找：
○ 按址查找：根据指定数据获取数据所在的位置(地址)
○ 按值查找：根据指定数据获取数据所在的位置序号
● 插入：在第i个结点前插入新节点
● 删除：删除第i个结点
● 单链表的建立
○ 头插法
○ 尾插法

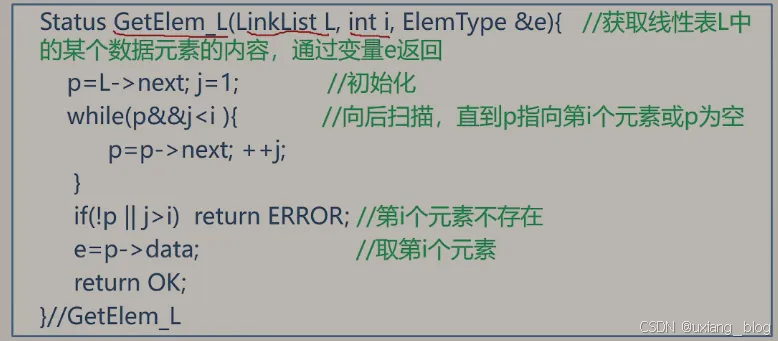
2.5.8.1、算法1：取值——取单链表中第i个元素的内容

思考：顺序表里如何找到第i个元素？L->elem[i-1] ——随机存储

注解：引入一个变量j来记录序号，从首元结点开始，即定义首元结点j=1，然后随着指针逐个往下走，依此逐个将j增加。有3种情况。
● 要是查找元素i不合法：比如i=-1,或者0，那么这样的数找不到，为了方便，链表中查找是根据逻辑顺序从1开始的，如果要查从-1，0这样不存在的，是不合法的，也会返回相应的ERROR。
● 如果查找元素i在范围内：比如i=3,则根据查找就会找到相应的数据 30。
● 如果查找元素i不在范围内：比如i=15，而实际上该单链表只能存储j=6个元素，所以超出范围后，就会返回NULL。

算法实现：
算法步骤:
● 1、从第1个结点(L->next)顺序扫描，用指针p扫描指向当前扫描到的结点，p初值p = p->next。
● 2、j 做计数器，累计当前扫描过的结点数，j初值为1；
● 3、当p指向扫描到的下一个结点时；计数器j加1。
● 4、当 j == i 时，p所指的结点就是要找的第i个结点。
算法描述：

2.5.8.2、算法2：查找——取单链表中第i个元素的内容

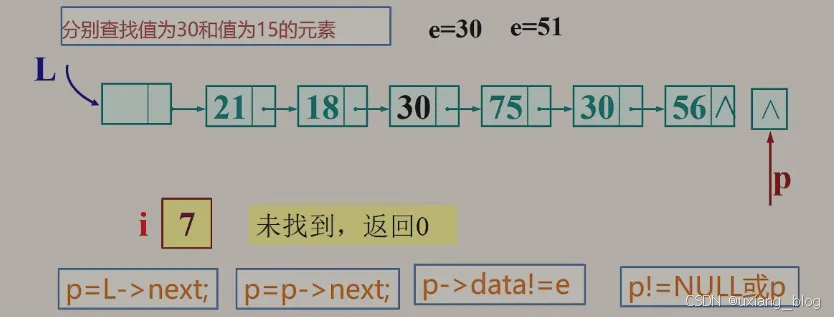
2.5.8.2.1、按值查找

按值查找：根据指定数据获取数据所在的位置（地址）。如果找到了就返回当前的位置（地址）p（比如：30），如果要返回第几个那就返回计数器的值（本例子结合上面的图是i的值）。

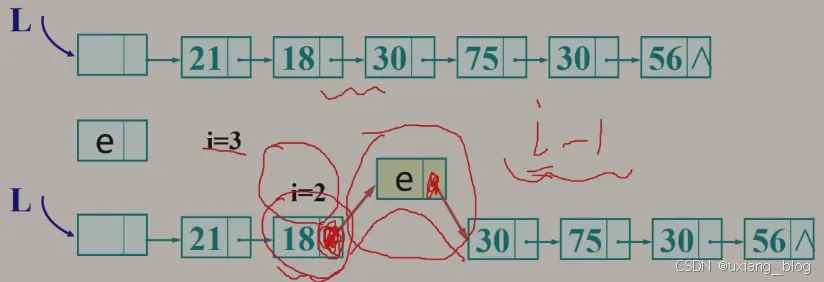
2.5.8.2.2、按值查找

2.5.8.3、算法3：插入——在第i个结点前插入值为e的新节点

算法步骤：

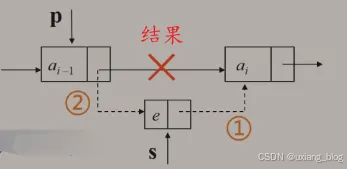
● 1、首先找到ai-1的存储位置p。
● 2、生成一个数据域为e的新节点s。
● 3、插入新结点：
○ （1）、新结点的指针域指向结点 ai：s->next = p -> next；
○ （2）、结点ai-1的指针域指向新节点：p -> next = s;
思考：步骤（1）和（2）能互换吗？先执行（2）后执行（1），可否？
注解：不可以，会丢失ai的地址。原来ai-1里面存储着ai的地址，互换之后就会丢失ai的地址，效果上面想当于砍断了ai-1和ai,在ai-1处接了一个s而已，如果在看砍断之前先用一个指针q记录下ai的地址，然后再砍断之后把q所记录ai的地址续在s上，这是可以的。
算法描述：

注解：需要掌握3点：
● 1、如果插入的？
● 2、怎么找到i-1个结点?
● 3、非法插入？怎么保证插入在i结点？

2.5.8.4、算法4：删除——删除第i个结点

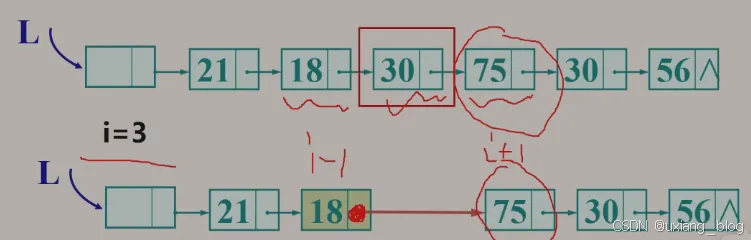
算法步骤：

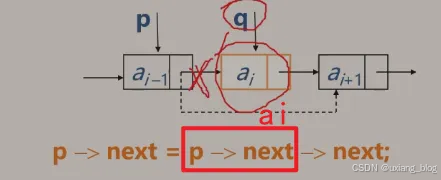
● 1、首先找到ai-1的存储位置p，保存要删除的ai的值。
● 2、令p -> next 指向ai+1。
● 释放结点ai的空间。
算法描述：

总结：算法2-5的时间效率分析：
单链表的查找、插入、删除算法时间效率分析
1、查找：因线性表只能顺序存取，即在查找时要从头指针找起，查找时间复杂度为O(n)。
2、插入和删除：
● 因线性链表不需要移动元素，只要修改指针，一般情况下时间复杂度为 O(1)。
● 但是，如果要在单链表中进行前插或删除操作，由于要从头查找前趋结点，所耗时间复杂度为O(n)。

2.5.8.5、算法5：单链表的建立

2.5.8.5.1、头插法——元素插入在链表头部，也叫前插法。

算法步骤：
● 1、从一个空表开始，重复读入数据;
● 2、生成新结点，将读入数据存放到新节点的数据域中
● 3、从最后一个结点开始，依此将各个结点插入到表的前端。

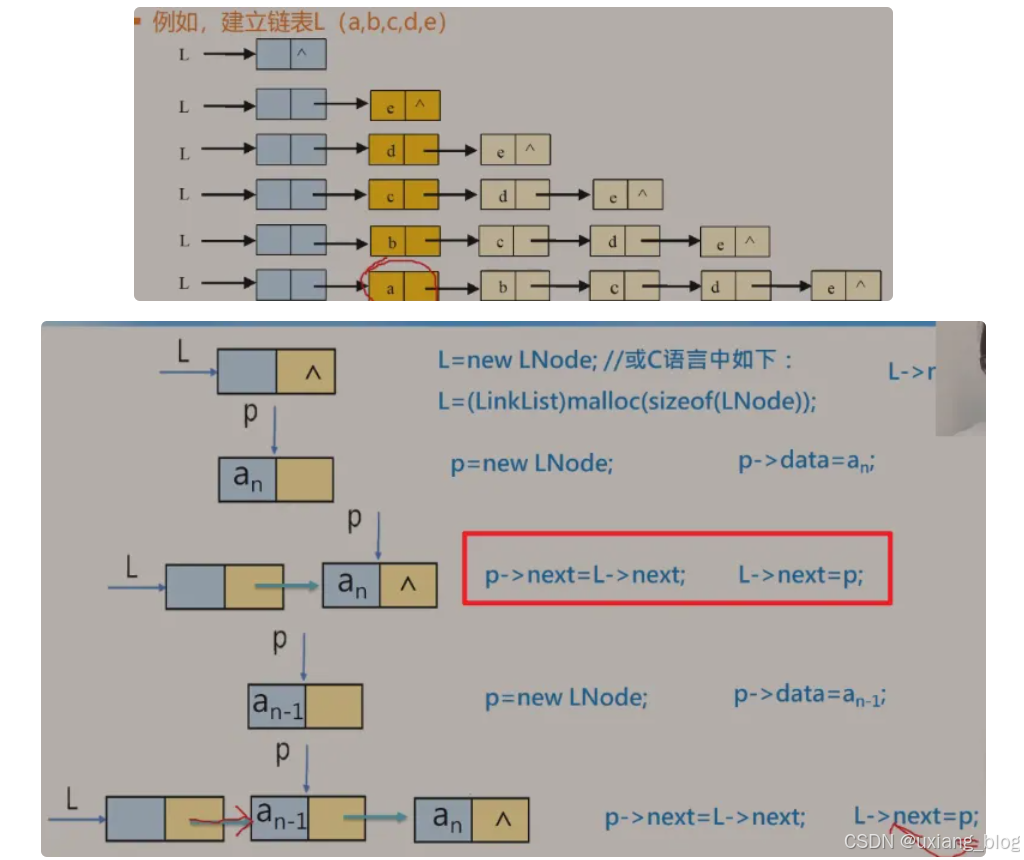
注解：p->next = L ->next; //把头结点的next中的NULL转换到新节点next中
L -> next = p；//然后再把新结点p赋值给头结点的next，就把新节点接到头结点L后面了。
后面接法如此重复。

算法描述：

2.5.8.5.2、尾插法——元素插入在链表尾部，也叫尾插法todo

算法步骤：
● 1、从一个空表L开始，将新结点逐个插入到链表的尾部，尾指针r指向链表的尾结点。
● 2、初始时,r同L均指向头结点。每读入一个数据元素则申请一个新结点，将新结点插入到尾结点后，r指向新结点。

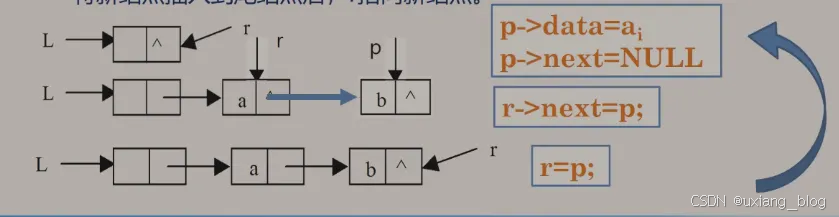
算法描述