【深度学习|学习笔记】从背景→公式→性质→梯度→何时用哪一个→数值稳定性与常见坑方面描述sigmoid和softmax函数!(一)
【深度学习|学习笔记】从背景→公式→性质→梯度→何时用哪一个→数值稳定性与常见坑方面描述sigmoid和softmax函数!(一)
【深度学习|学习笔记】从背景→公式→性质→梯度→何时用哪一个→数值稳定性与常见坑方面描述sigmoid和softmax函数!(一)
文章目录
- 【深度学习|学习笔记】从背景→公式→性质→梯度→何时用哪一个→数值稳定性与常见坑方面描述sigmoid和softmax函数!(一)
- 1) 背景与直觉
- 2) 定义与公式
- Sigmoid(logistic 函数)
- Softmax
- 性质:
- 3) 使用场景与差异
- 阈值与决策:
- 温度(Temperature):
- 4) 数值稳定性与训练注意
- 永远对 logits 使用稳定接口:
- 饱和与梯度消失:
- 类别不平衡:
- 校准:
欢迎铁子们点赞、关注、收藏!
祝大家逢考必过!逢投必中!上岸上岸上岸!upupup
大多数高校硕博生毕业要求需要参加学术会议,发表EI或者SCI检索的学术论文会议论文。详细信息可扫描博文下方二维码 “
学术会议小灵通”或参考学术信息专栏:https://blog.csdn.net/2401_89898861/article/details/148877490
1) 背景与直觉
- sigmoid 用于“二分类/单神经元输出”的概率映射:把一个实数 logit 映到 (0,1)。
- softmax 用于“多分类(互斥)/多神经元输出”的概率归一化:把一个 logits 向量 映到 K 维概率单纯形(各分量∈(0,1),且总和=1)。
从优化角度看:
- 二分类逻辑回归 ←→ sigmoid + 二分类交叉熵。
- 多分类逻辑回归 ←→ softmax + 多分类交叉熵。
2) 定义与公式
Sigmoid(logistic 函数)
定义:
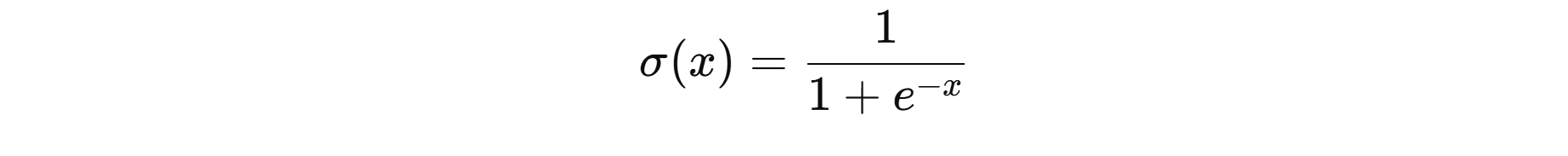
性质:
- 输出范围 (0,1);对称点在 x=0⇒σ(0)=0.5x=0 ⇒ σ(0)=0.5x=0⇒σ(0)=0.5;单调递增、两端饱和。
导数:
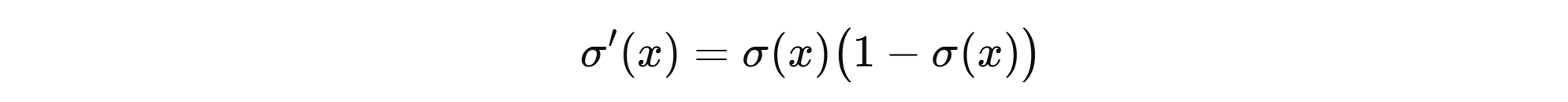
导数:损失(带 logits 的二分类交叉熵)(数值稳定写法,标签 y∈0,1y∈{0,1}y∈0,1,logit = z)
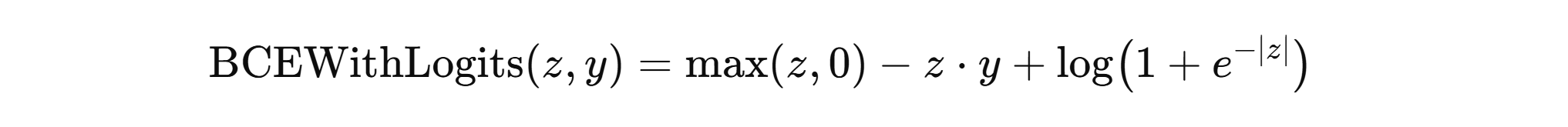
Softmax
- 对 K 维 logits 向量 z=(z1,…,zK)z=(z_1,…,z_K)z=(z1,…,zK):
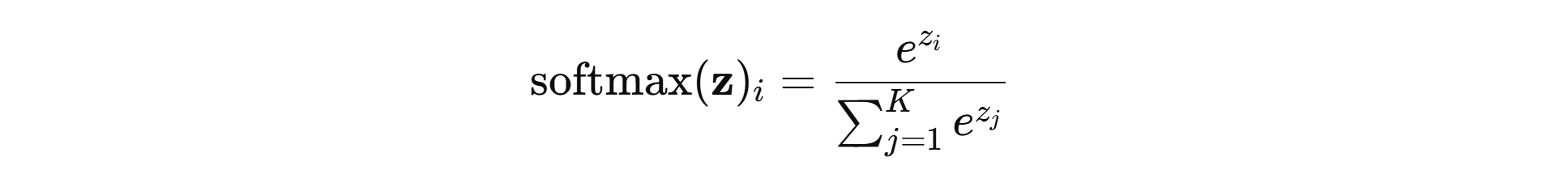
性质:
- 输出为概率分布,所有分量相加为 1。
- 雅可比矩阵(梯度):
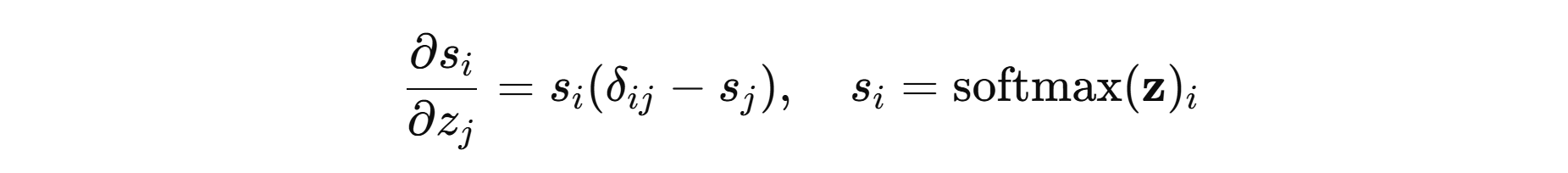
- 损失(多分类交叉熵)(数值稳定写法,真类索引为 yyy):
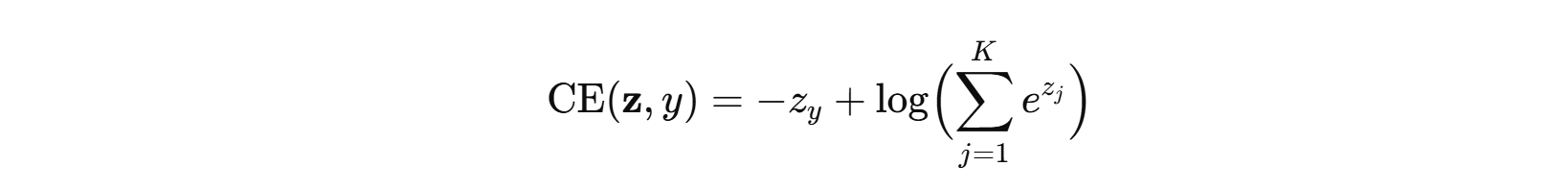
- 常用 log-sum-exp trick:先减去 max(z)max(z)max(z) 再取 exp,避免上溢。
- 联系: softmax 在 K=2 时退化为 sigmoid:
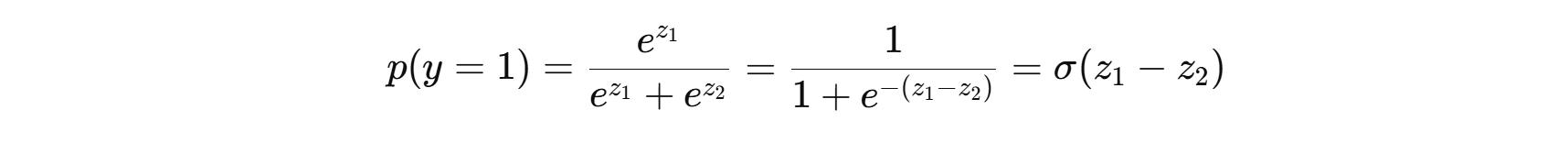
- 若固定 z2=0z_2=0z2=0,p(y=1)=σ(z1)p(y=1)=σ(z_1)p(y=1)=σ(z1)。
3) 使用场景与差异
| 场景 | 该用谁 | 说明 |
|---|---|---|
| 二分类(单输出概率) | sigmoid | 每个样本一个 logit→概率;配 BCE(带 logits)。 |
| 多分类(互斥) | softmax | K 个互斥类别;输出归一的 K 维概率;配交叉熵。 |
| 多标签(非互斥) | 多个 sigmoid | 每个类别独立是/否;不互斥;每类配一个 BCE。 |
阈值与决策:
- Sigmoid:常用 0.5 或根据 ROC/PR 调整阈值。
- Softmax:取 argmax(也可做温度缩放与阈值化)。
温度(Temperature):
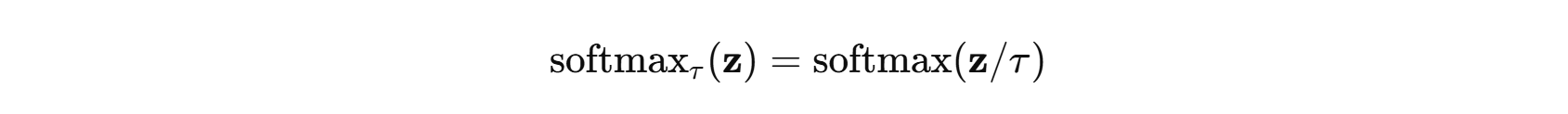
- τ→0:更“尖锐”,趋近 one-hot;
- τ→∞:更“平滑”,接近均匀分布。
4) 数值稳定性与训练注意
永远对 logits 使用稳定接口:
- PyTorch:
BCEWithLogitsLoss、CrossEntropyLoss(二者都直接吃 logits,内部自带 sigmoid/softmax + 稳定计算)。 - 自己实现 softmax 时:先
z -= z.max(axis)再np.exp(z)。
饱和与梯度消失:
- sigmoid 在 ∣x∣ 大时梯度 →0。深层网络里更偏向使用 ReLU 系列做隐藏层激活,仅在输出层用
sigmoid/softmax。
类别不平衡:
- 可用加权损失、focal loss 或重采样策略。
校准:
- Softmax 概率有时过度自信,可用温度缩放(后处理)改善校准。
