C++宽度优先搜索算法:队列与优先级队列
本期我们就来深入学习一下C++算法中一个很重要的算法思想:宽度优先搜索算法
宽度优先算法是一个应用十分广泛的算法思想,涉及的领域也十分繁多,因此本篇我们先只涉猎它的一部分算法题:队列/优先级队列,后续我们会进一步地补充。
相关题解代码已经上传至作者的个人gitee:楼田莉子/C++算法学习喜欢请点个赞谢谢
目录
基本概念
算法步骤
时间复杂度分析
应用场景
广度优先搜索(BFS) vs. 深度优先搜索(DFS)算法对比
1、N叉树的层序遍历
2、二叉树的锯齿形层序遍历
3、二叉树最大宽度
4、在每个树行中找最大值
5、最后一块石头的重量
6、数据流中的第K大元素
为什么选择小根堆?
大根堆的缺点
7、前K个高频单词
基本概念
宽度优先搜索(Breadth-First Search,简称BFS)是一种用于遍历或搜索树或图数据结构的算法。它从根节点开始,首先访问所有相邻节点,然后再逐层向下访问更远的节点。BFS属于盲目搜索算法,不使用问题领域的任何启发式信息。
算法步骤
-
初始化:
- 创建一个队列Q用于存储待访问节点
- 将起始节点S标记为已访问(通常使用颜色标记或布尔数组)
- 将S加入队列Q
-
循环处理:
- 当Q不为空时: a. 从Q中取出队首节点V b. 访问节点V(根据具体应用可能是检查、处理等操作) c. 将V的所有未被访问的邻接节点标记为已访问并加入队列Q
-
终止条件:
- 当队列为空时,算法结束
时间复杂度分析
- 邻接表表示:O(V + E),其中V是顶点数,E是边数
- 邻接矩阵表示:O(V²)
- 空间复杂度:O(V)(最坏情况下需要存储所有节点)
应用场景
-
最短路径问题:
- 在无权图中寻找两个节点间的最短路径
- 示例:迷宫求解、社交网络中寻找最少中间人
-
网络爬虫:
- 搜索引擎爬虫按层级抓取网页
- 先抓取种子页面,然后抓取这些页面链接的所有页面
-
广播网络:
- 在计算机网络中传播信息包
- 在P2P网络中定位资源
-
社交网络分析:
- 寻找某人的N度人际关系
- 计算社交影响力
-
连通性检测:
- 检查图中所有节点是否连通
- 寻找图中的连通分量
广度优先搜索(BFS) vs. 深度优先搜索(DFS)算法对比
| 特性维度 | 广度优先搜索 (BFS) | 深度优先搜索 (DFS) |
|---|---|---|
| 核心数据结构 | 队列 (Queue) (FIFO) | 栈 (Stack) (LIFO) (或系统的递归调用栈) |
| 遍历思想/顺序 | 逐层遍历 (Level Order)。从起点开始,优先访问所有相邻节点,再访问相邻节点的相邻节点。 | 一路到底 (Depth Order)。从起点开始,沿着一条路径尽可能深地探索,直到尽头再回溯。 |
| 空间复杂度 | O(b^d) (对于树结构,b为分支因子,d为目标所在深度) 在最坏情况下,需要存储一整层的节点,对于空间消耗较大。 | O(h) (对于树结构,h为树的最大深度) 通常只需存储当前路径上的节点,空间消耗相对较小。 |
| 完备性 | 是。如果解存在,BFS(在有限图中)一定能找到解。 | 否(无限图)。如果树深度无限且解不在左侧分支,DFS可能永远无法找到解。在有限图中是完备的。 |
| 最优性 | 是(未加权图)。BFS按层扩展,首次找到的目标节点一定是经过边数最少的(最短路径)。 | 否。DFS找到的解不一定是路径最短的,它取决于遍历顺序和运气。 |
| 常见应用场景 | 1. 寻找最短路径(未加权图) 2. 系统性的状态空间搜索(如谜题求解) 3. 查找网络中所有节点(如社交网络的“好友推荐”) | 1. 拓扑排序 2. 检测图中环 3. 路径查找(所有可能解,如迷宫问题) 4. 图的连通分量分析 |
| 实现方式 | 通常使用迭代和队列实现。 | 使用递归实现最简洁,也可使用迭代和显式栈(Stack) 实现。 |
| 直观比喻 | “水波纹”扩散:像一块石头投入水中,涟漪一圈一圈地向外扩展。 | “走迷宫”:选择一条路一直走下去,直到死胡同,然后返回到最后一个岔路口选择另一条路。 |
1、N叉树的层序遍历

算法思想:
/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:vector<vector<int>> levelOrder(Node* root) {if(root==nullptr) return {};vector<vector<int>> ret;queue<Node*>q;q.push(root);while(!q.empty()){vector<int>level;int n=q.size();//求本层的个数for(int i=0;i<n;i++){Node* cur=q.front();q.pop();level.push_back(cur->val);for(auto& x:cur->children)//下一层结点入队{q.push(x);}}ret.push_back(level);}return ret;}
};2、二叉树的锯齿形层序遍历
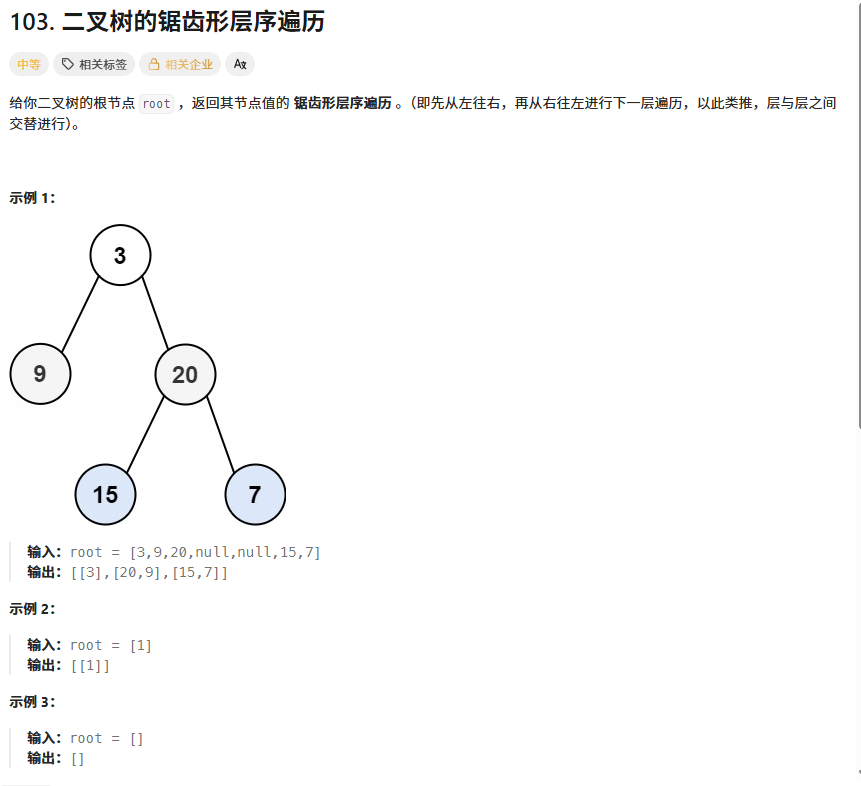
算法思想:
-
广度优先搜索(BFS):使用队列进行标准的层序遍历,按层处理节点。
-
方向标志:使用一个布尔变量
Is来标记当前层是否需要反转。初始为false,表示第一层从左到右。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {if(root==nullptr) return {}; // 如果根节点为空,返回空数组vector<vector<int>>ret; // 存储最终结果queue<TreeNode*>q; // 辅助队列用于BFSq.push(root); // 将根节点加入队列bool Is=false; // 方向标志,false表示从左到右,true表示从右到左while(!q.empty()){ vector<int>level; // 存储当前层的节点值int n=q.size(); // 当前层的节点数for(int i=0;i<n;i++){auto it=q.front(); // 取出队首节点q.pop();level.push_back(it->val); // 将节点值加入当前层数组if(it->left) q.push(it->left); // 将左子节点加入队列if(it->right) q.push(it->right); // 将右子节点加入队列} if(Is) // 如果需要反转当前层{reverse(level.begin(),level.end()); // 反转当前层数组ret.push_back(level); // 将反转后的数组加入结果Is=!Is; // 切换方向标志} else // 如果不需要反转{ret.push_back(level); // 直接加入结果Is=!Is; // 切换方向标志}} return ret; // 返回最终结果}
};3、二叉树最大宽度
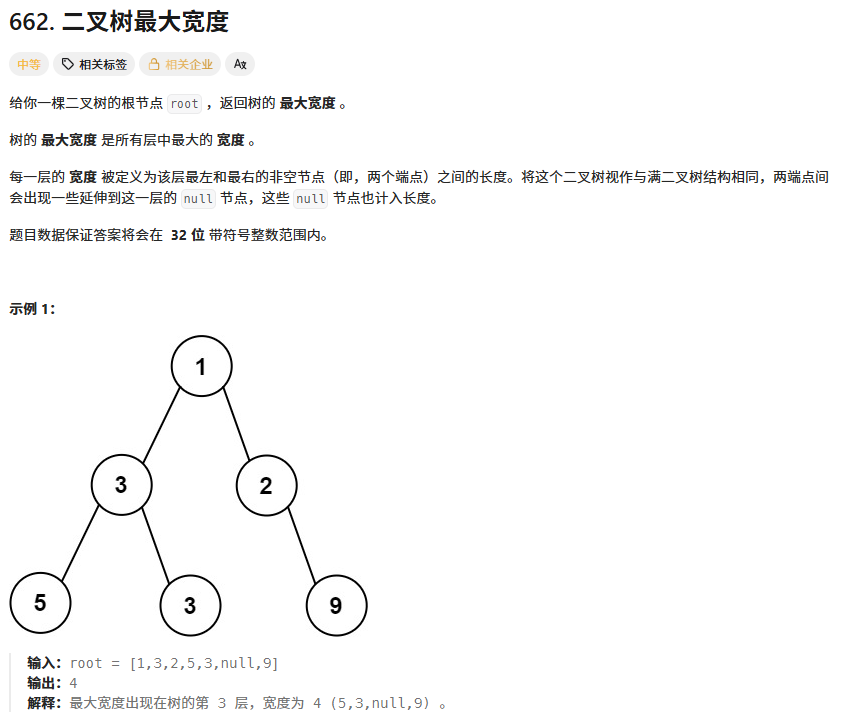
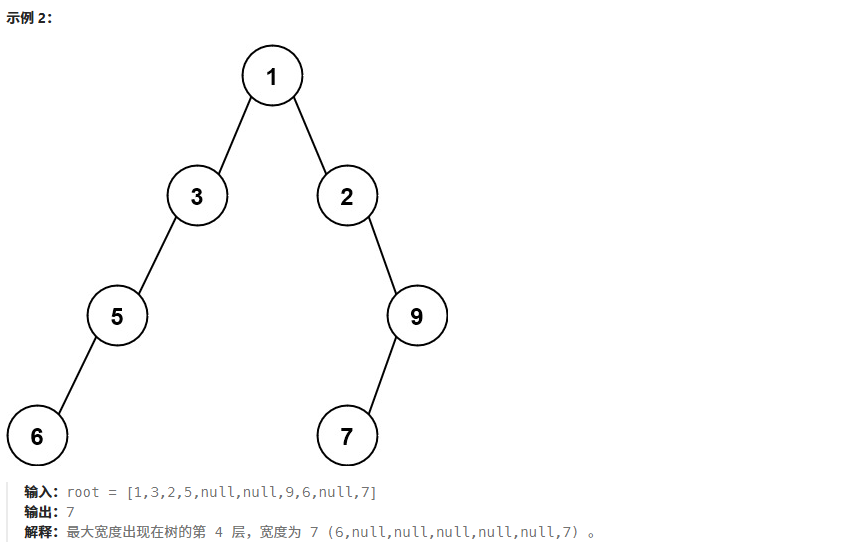
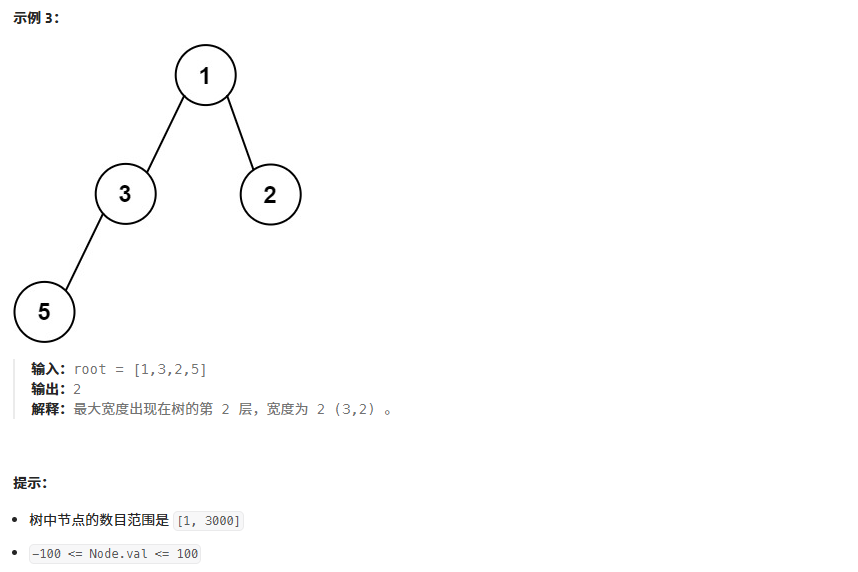
算法思想:利用数组存储二叉树的方式,给结点编号
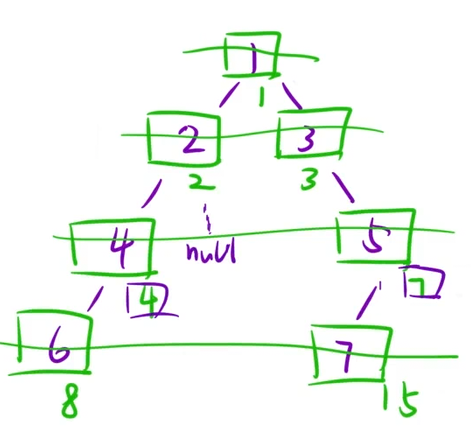
细节:下标有可能溢出
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int widthOfBinaryTree(TreeNode* root) {vector<pair<TreeNode*,unsigned int>>q;//数组模拟队列q.push_back({root,1});unsigned int ret=0;//统计最终结果while(q.size()){//先更新auto&[x1,y1]=q[0];auto&[x2,y2]=q.back();ret=max(ret,y2-y1+1);//下一层进队vector<pair<TreeNode*,unsigned int>>tmp;//下一层进第二个组for(auto&[x,y]:q){if(x->left) tmp.push_back({x->left,y*2});if(x->right) tmp.push_back({x->right,y*2+1});}q=tmp;}return ret;}
};4、在每个树行中找最大值
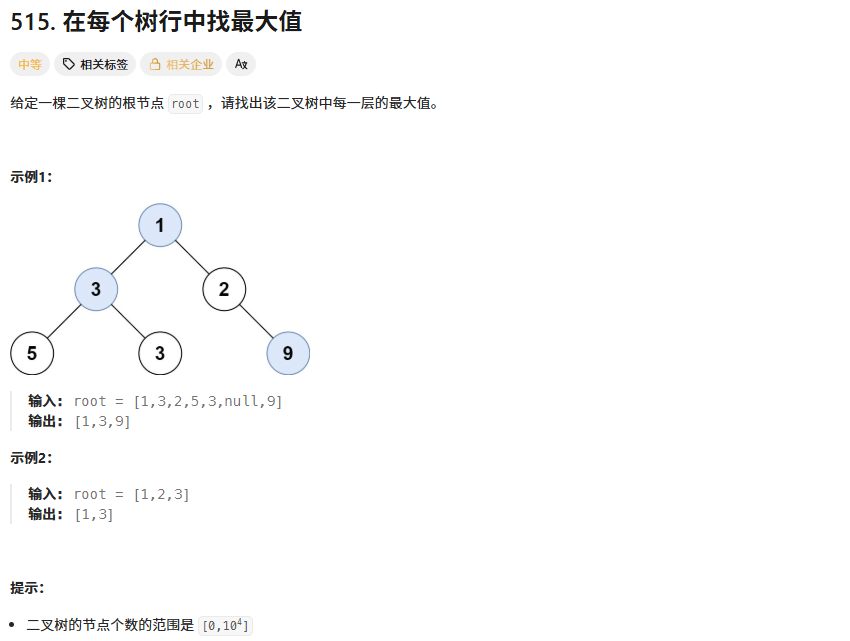
算法思想:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> largestValues(TreeNode* root) {if(root==nullptr) return {};vector<int>ret;queue<TreeNode*>q;q.push(root);while(!q.empty()){TreeNode*cur=root;int n=q.size();int a=INT_MIN;//初始化为无穷小for(int i=0;i<n;i++){auto it=q.front();q.pop();a=max(a,it->val);if(it->left) q.push(it->left);if(it->right) q.push(it->right);}ret.push_back(a);}return ret;}
};5、最后一块石头的重量

算法思想:
class Solution {
public:int lastStoneWeight(vector<int>& stones) {// 创建一个大根堆(优先级队列默认是最大堆)// 这意味着队列顶部始终是当前最大的元素priority_queue<int> q;// 将所有石头重量加入优先级队列for(auto& x : stones){q.push(x);}// 循环处理,直到队列中只剩下一块石头或没有石头while(q.size() > 1){// 取出当前最重的石头int a = q.top();q.pop();// 取出当前第二重的石头int b = q.top();q.pop();// 如果两块石头重量不相等,将差值重新加入队列if(a > b) q.push(a - b);// 如果相等,两者都粉碎,不需要操作(相当于都不加入队列)}// 检查队列是否还有剩余石头:如果有,返回顶部元素(最后一块石头的重量);否则返回0return q.size() ? q.top() : 0;}
};6、数据流中的第K大元素


算法思想:Top-K问题
堆(O(N*logk))或者快速选择算法(O(N))
1、创建大根堆或者小根堆
2、元素一个一个进堆
3、判断堆的大小是否超过K
class KthLargest {//创建一个大小为k的小根堆priority_queue<int,vector<int>,greater<int>>heap;int _k;public:KthLargest(int k, vector<int>& nums) {_k=k;for(auto&x:nums){heap.push(x);if(heap.size()>_k) heap.pop();}}int add(int val) {heap.push(val);if(heap.size()>_k) heap.pop();return heap.top();}
};/*** Your KthLargest object will be instantiated and called as such:* KthLargest* obj = new KthLargest(k, nums);* int param_1 = obj->add(val);*/为什么选择小根堆?
-
问题需求:我们需要实时返回数据流中第K大的元素。这意味着我们需要维护前K大的元素,但只关心其中最小的那个(即第K大的元素)。
-
小根堆的优势:
-
维护一个大小为K的小根堆,堆顶元素即为第K大的元素(因为堆顶是堆中最小的元素,而堆中所有元素都是当前最大的K个元素)。
-
添加新元素时,如果新元素大于堆顶元素,则替换堆顶并调整堆,时间复杂度为O(log K)。查询操作直接返回堆顶,时间复杂度为O(1)。
-
整体效率高,适合数据流频繁添加和查询的场景。
-
大根堆的缺点
-
效率低下:如果使用大根堆存储所有元素,每次查询第K大的元素时,需要从堆中弹出K-1个元素才能访问到第K大的元素。这会破坏堆的结构,且每次查询的时间复杂度为O(K log n)(因为弹出操作需要调整堆)。
-
空间浪费:大根堆需要存储所有元素,而不仅仅是前K大的元素,因此空间复杂度为O(n),而不是O(K)。
-
查询成本高:每次查询都需要执行弹出和重新插入操作(或者复制堆),导致整体性能较差,尤其当K较大或数据流很大时,无法满足实时性要求。
大根堆的代码(不推荐这个写法)
#include <vector>
#include <queue>
using namespace std;class KthLargest {
private:priority_queue<int> maxHeap; // 大根堆,存储所有元素int k;public:KthLargest(int k, vector<int>& nums) {this->k = k;for (int num : nums) {maxHeap.push(num);}}int add(int val) {maxHeap.push(val); // 添加新元素到大根堆// 创建临时堆副本,避免破坏原堆priority_queue<int> temp = maxHeap;// 弹出K-1个最大元素,使堆顶变为第K大的元素for (int i = 0; i < k - 1; i++) {temp.pop();}return temp.top(); // 返回第K大的元素}
};7、前K个高频单词

class Solution
{
public://老方法:stable_sort函数(稳定排序)// 仿函数// struct compare// {// bool operator()(const pair<string ,int>&kv1,const pair<string ,int>&kv2)// {// return kv1.second>kv2.second;// }// };// vector<string> topKFrequent(vector<string>& words, int k) // {// map<string ,int>countMap;// for(auto& str:words)// {// //统计次数// countMap[str]++;// }// //数据量很大的时候要建小堆// //数据量不大用大堆// //但是这里要按频率所以不建议用小堆// //用排序和大堆都差不多// //不可以用sort直接去排序// //sort要求是随机迭代器,只用string、vector、deque支持// vector<pair<string,int>>v(countMap.begin(),countMap.end());// //sort(v.begin(),v.end(),compare());// //sort不是一个稳定的排序// stable_sort(v.begin(),v.end(),compare());//稳定的排序算法// vector<string>ret;// //取出k个// for(int i=0;i<k;i++)// {// ret.push_back(v[i].first);// }// return ret;//方法二:仿函数//仿函数// struct compare// {// bool operator()(const pair<string ,int>&kv1,const pair<string ,int>&kv2)// {// return kv1.second>kv2.second||(kv1.second==kv2.second&&kv1.first<kv2.first);// }// };// vector<string> topKFrequent(vector<string>& words, int k) // {// map<string ,int>countMap;// for(auto& str:words)// {// //统计次数// countMap[str]++;// }// //数据量很大的时候要建小堆// //数据量不大用大堆// //但是这里要按频率所以不建议用小堆// //用排序和大堆都差不多// //不可以用sort直接去排序// //sort要求是随机迭代器,只用string、vector、deque支持// vector<pair<string,int>>v(countMap.begin(),countMap.end());// //仿函数可以控制比较逻辑// sort(v.begin(),v.end(),compare());//稳定的排序算法// vector<string>ret;// //取出k个// for(int i=0;i<k;i++)// {// ret.push_back(v[i].first);// }// return ret;//方法三:优先级队列struct compare{bool operator()(const pair<string, int>& kv1, const pair<string, int>& kv2) const{// 比较逻辑:频率高优先,频率相同则字典序小优先return kv1.second < kv2.second || (kv1.second == kv2.second && kv1.first > kv2.first);}};vector<string> topKFrequent(vector<string>& words, int k) {map<string, int> countMap;for(auto& str : words){countMap[str]++;}//数据量很大的时候要建小堆//数据量不大用大堆//但是这里要按频率所以不建议用小堆//用排序和大堆都差不多//不可以用sort直接去排序//sort要求是随机迭代器,只用string、vector、deque支持//建立大堆//priority_queue默认为大堆//不写仿函数的时候priority_queue按pair比,pair默认按小于比// - 元素类型: pair<string, int>// - 容器类型: vector<pair<string, int>>// - 比较器类型: compare (去掉括号)priority_queue<pair<string, int>,vector<pair<string, int>>,compare> pq(countMap.begin(), countMap.end());vector<string> ret;for(int i = 0; i < k; i++){ret.push_back(pq.top().first);pq.pop();}return ret;}
};
本期内容就到这里,喜欢请点个赞谢谢
