25年8月通信基础知识补充2:星座的峭度(Kurtosis)、ISAC
看文献过程中不断发现有太多不懂的基础知识,故长期更新这类blog不断补充在这过程中学到的知识。由于这些内容与我的研究方向并不一定强相关,故记录不会很深入请见谅。
【通信基础知识补充9】25年8月通信基础知识补充2:星座的峭度(Kurtosis)
- 一、星座的峭度
- 1.1 基本信号模型
- 1.2 星座的峭度(Kurtosis)
- 1.3 不同调制方式的峭度
- 1.4 三类星座的分类
- 1.4.1 Gaussian Constellation(高斯星座)
- 1.4.2 Sub-Gaussian Constellations(亚高斯星座,μ4<2\mu_4 < 2μ4<2)
- 1.4.3 Super-Gaussian Constellations(超高斯星座,μ4>2\mu_4 > 2μ4>2)
- 1.4.4 对比总结表
- 1.5 应用与意义
- 1.6 峭度和ISAC的关系
- 1.6.1 ISAC 的核心矛盾
- 1.6.2 峭度和 ISAC 的关系
- 1.5.3 举例
一、星座的峭度
1.1 基本信号模型
-
随机符号
定义符号向量:s=[s1,s2,…,sN]T∈CN×1s = [s_1, s_2, \dots, s_N]^T \in \mathbb{C}^{N \times 1} s=[s1,s2,…,sN]T∈CN×1
这里的 sis_isi 是从一个星座集合 S\mathcal{S}S 中独立同分布(i.i.d.)抽取的复数符号。
-
归一化约束
E(∣s∣2)=1,E(s)=E(s2)=0\mathbb{E}(|s|^2) = 1, \quad \mathbb{E}(s) = \mathbb{E}(s^2) = 0 E(∣s∣2)=1,E(s)=E(s2)=0
意味着平均能量归一化为 1,并且星座点对称分布在原点附近(零均值、零二阶矩)。
1.2 星座的峭度(Kurtosis)
-
定义公式
在通信里,星座峭度主要用来刻画调制符号的幅度分布特性,具体而言,峭度衡量分布的“尖锐”程度,定义如下:μ4≜E{∣s−E(s)∣4}E{∣s−E(s)∣2}2\mu_4 \triangleq \frac{\mathbb{E}\{ |s - \mathbb{E}(s)|^4 \}}{\mathbb{E}\{ |s - \mathbb{E}(s)|^2 \}^2} μ4≜E{∣s−E(s)∣2}2E{∣s−E(s)∣4}
因为 E(s)=0\mathbb{E}(s)=0E(s)=0(解释:因为PSK, QAM, APSK等调制的星座点分布关于原点对称,因此没有直流(DC)分量),所以公式简化为:
μ4=E(∣s∣4)\mu_4 = \mathbb{E}(|s|^4) μ4=E(∣s∣4)
-
物理意义
峭度体现了符号幅度分布与高斯分布的差异:- 峭度大:符号幅度分布更“尖锐”,集中在零点附近,但尾部更重。
- 峭度小:分布更平坦,符号分布相对均匀。
1.3 不同调制方式的峭度
下表给出了常见星座的数值:

- PSK:幅度恒定,峭度最低(=1),因为能量均匀分布在相位上。
- QAM:随着阶数升高,峭度逐渐增加(约在 1.3~1.4 之间),意味着幅度分布比 PSK 更接近高斯。
1.4 三类星座的分类
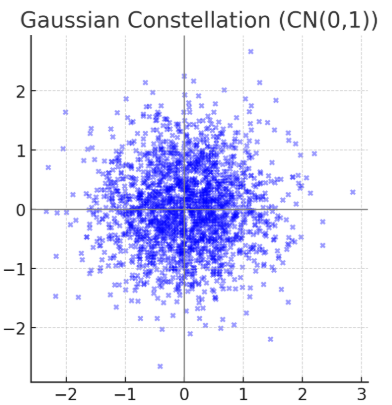
1.4.1 Gaussian Constellation(高斯星座)
-
定义:μ4=2\mu_4 = 2μ4=2,对应于复高斯分布 s∼CN(0,1)s \sim \mathcal{CN}(0,1)s∼CN(0,1)。
-
特性:
- 理论基准(通常不可直接实现)。
- 幅度与相位连续分布,满足圆对称。
- 在香农容量推导、互信息分析中常作为理想输入分布。
-
优势:
- 能量分布最均衡,最大化香农容量。
- 是评估各种实际调制方式(QAM、PSK、APSK 等)性能的 比较基准。
-
不足:
- 工程上难以实现,因为需要无限个星座点。
- 实际系统只能用有限阶调制去逼近。
1.4.2 Sub-Gaussian Constellations(亚高斯星座,μ4<2\mu_4 < 2μ4<2)
- 典型例子:
- PSK(恒幅,相位均匀分布,μ4=1\mu_4 = 1μ4=1)。
- QAM(16-QAM, 64-QAM, μ4≈1.3∼1.4\mu_4 \approx 1.3\sim1.4μ4≈1.3∼1.4)。
- 特性:
- 分布比高斯“平坦”,符号幅度差别小。
- 尾部轻,没有特别极端的高能量点。
- 优势:
- 功放友好:幅度变化小,峰均功率比 (PAPR) 低,非线性失真影响小。
- 实现简单:QAM/PSK 星座点规则,便于硬件调制解调。
- 广泛应用:几乎所有蜂窝通信(4G/5G)、WLAN、卫星通信(部分场景)都基于 QAM/PSK。
- 不足:
- 相比 Gaussian 输入,容量略有损失。
- QAM 高阶化后抗噪性能下降。
1.4.3 Super-Gaussian Constellations(超高斯星座,μ4>2\mu_4 > 2μ4>2)
-
典型例子:
- APSK(Amplitude and Phase Shift Keying,尤其是环间幅度差异大时)。
- Index Modulation (IM)(多数符号为零,少数符号有大能量)。
- 稀疏调制方式(Sparse Signaling)。
-
特性:
- 分布更“尖锐”,大多数符号集中在低能量区,少数符号能量特别大。
- 有重尾 (heavy-tail),能量波动显著。
-
优势:
- 频谱效率高:通过稀疏或幅度差异扩展符号集。
- 适合卫星通信:APSK 能兼顾高频谱效率与非线性鲁棒性(DVB-S2/S2X 标准广泛采用)。
- 适合 ISAC / 稀疏场景:Index Modulation 在高维信道里稀疏映射,利于感知与通信联合。
-
不足:
- PAPR 高:对功放非线性更敏感。
- 检测复杂度高,接收端需做稀疏检测或环半径估计。
1.4.4 对比总结表
| 类别 | 峭度 μ4\mu_4μ4 | 典型星座 | 分布特性 | 工程优势 | 主要不足 |
|---|---|---|---|---|---|
| Gaussian | =2=2=2 | 理想高斯输入 | 圆对称、能量最均衡 | 达到香农容量,理论基准 | 不可实现 |
| Sub-Gaussian | <2<2<2 | QAM, PSK | 平坦,幅度差小 | PAPR 低,硬件友好,广泛应用 | 容量略低 |
| Super-Gaussian | >2>2>2 | APSK, IM | 尖锐+长尾,能量波动大 | 频谱效率高,适合卫星/稀疏场景 | PAPR 高,检测复杂 |
- Gaussian → 理想基准(理论分析)。
- Sub-Gaussian → 工程主流(QAM/PSK,低 PAPR,硬件友好)。
- Super-Gaussian → 特殊场景优选(卫星 APSK,IM 稀疏通信/感知)。
1.5 应用与意义
峭度是 信号统计特性的重要指标,在以下方面有应用:
- 信道建模与容量分析:非高斯输入分布会影响互信息和误码率性能。
- 信号检测与盲估计:高阶统计量(如峭度)常用于调制识别、盲均衡等。
- ISAC(感知通信一体化):峭度影响旁瓣水平与干扰特性。
- 非线性效应分析:星座的幅度分布与光纤/功放的非线性响应紧密相关。
1.6 峭度和ISAC的关系
1.6.1 ISAC 的核心矛盾
在 ISAC 里,一个波形既要用于 通信,又要用于 感知(雷达探测/成像)。
- 通信需求:高频谱效率、低误码率 → 常用 QAM、PSK。
- 感知需求:低旁瓣、良好的模糊函数特性(时延-多普勒域分辨率高)。
1.6.2 峭度和 ISAC 的关系
星座峭度影响 波形的功率分布,而功率分布会进一步影响 通信-感知性能权衡:
-
旁瓣水平(sidelobe level)
- 峭度小(PSK, Sub-Gaussian)→ 符号幅度均匀,能量分布平稳,平均旁瓣水平较低。
- 峭度大(APSK, Super-Gaussian)→ 能量分布不均匀,可能导致旁瓣增强。
感知性能(比如目标检测、测距精度)和峭度强相关。
-
抗非线性与功放效率
- ISAC 系统常用高功率放大器(如卫星、车载雷达),波形的峰均功率比(PAPR)越大越容易失真。
- 峭度和 PAPR 正相关 → 峭度大,功放效率低。
峭度小的调制方式在 ISAC 系统里更容易保持波形一致性。
-
调制方式选择
- 通信喜欢高阶 QAM(吞吐量高),但峭度较大。
- 感知更喜欢幅度均匀的 PSK(旁瓣低)。
峭度提供了一个 量化指标,用来评估星座是否适合 ISAC。
1.5.3 举例
- QPSK (峭度=1):能量分布均匀 → 感知性能好(旁瓣低),但通信速率低。
- 64-QAM (峭度≈1.36):吞吐量高,但幅度差别大 → 功放非线性、旁瓣增加,感知性能下降。
- APSK (峭度>2):有时用于卫星通信,峰度大,感知旁瓣更差。
总结: 在 ISAC 中,星座的峭度是一个桥梁指标,它刻画调制星座的能量分布特性,直接影响通信的非线性鲁棒性和感知的旁瓣性能,从而帮助设计和选择更适合 ISAC 的波形。

