PyTorch损失函数全解析与实战指南
以下是更详细的 PyTorch 损失函数解析，涵盖数学公式、适用场景、优缺点对比及代码示例：
1. 回归损失函数（Regression Losses）
(1) L1Loss (Mean Absolute Error, MAE)
- 公式:
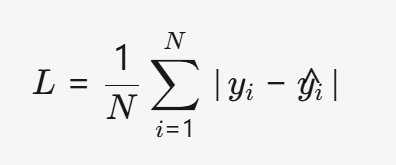
- 特点:
- 对异常值鲁棒（因为绝对值函数梯度恒定）。
- 梯度不随误差大小变化，可能导致收敛慢。
- 适用场景:
- 目标变量存在异常值时（如房价预测）。
- 需要稳定梯度的场景。
(2) MSELoss (Mean Squared Error, MSE)
- 公式:
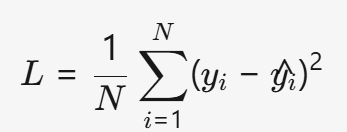
- 特点:
- 对误差大的样本惩罚更重（平方放大了异常值影响）。
- 梯度随误差增大而增大，可能收敛更快。
- 适用场景:
- 数据干净且异常值较少时（如物理实验预测）。
- 需要强信号指导优化的任务。
(3) SmoothL1Loss
- 公式:
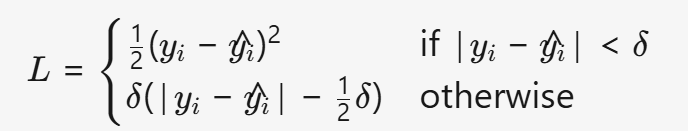
- 特点:
- 结合MSE和L1的优点：小误差时平滑，大误差时鲁棒。
- 避免MSE的梯度爆炸问题。
- 适用场景:
- 目标检测中的边界框回归（如Faster R-CNN）。
- 需要平衡精度和鲁棒性的任务。
(4) HuberLoss (Smooth Mean Absolute Error)
- 公式:
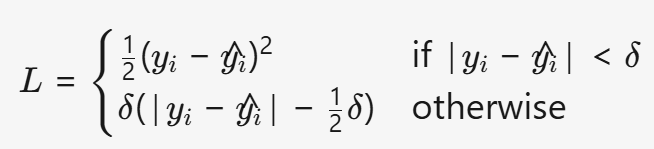
- 特点:
- 可调节超参数δ控制鲁棒性。
- 比SmoothL1Loss更灵活。
- 适用场景:
- 需要动态调整鲁棒性的回归任务（如金融预测）。
(5) KLDivLoss (Kullback-Leibler Divergence)
- 公式:
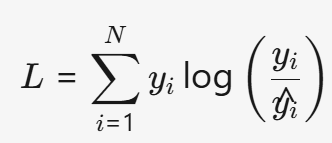
- 特点:
- 衡量两个概率分布的差异（非对称）。
- 常用于生成模型（如GANs、VAEs）。
- 适用场景:
- 概率分布对齐（如文本生成、图像生成）。
2. 分类损失函数（Classification Losses）
(1) NLLLoss (Negative Log-Likelihood)
- 公式:
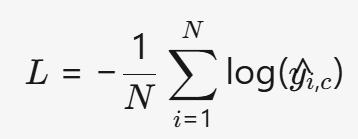（y^i,c是样本i属于类别c的概率） - 特点:
- 要求输入是log概率（通常配合LogSoftmax使用）。
- 数值稳定（避免log(0)问题）。
- 适用场景:
- 多分类任务（如图像分类）。
(2) BCELoss (Binary Cross-Entropy)
- 公式:
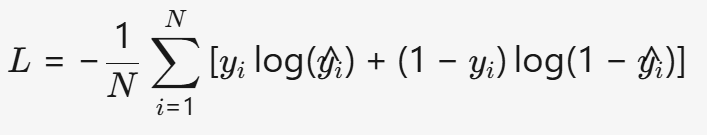
- 特点:
- 直接处理0-1概率输出（需配合Sigmoid）。
- 对类别不平衡敏感。
- 适用场景:
- 二分类任务（如垃圾邮件检测）。
(3) BCEWithLogitsLoss
- 公式:
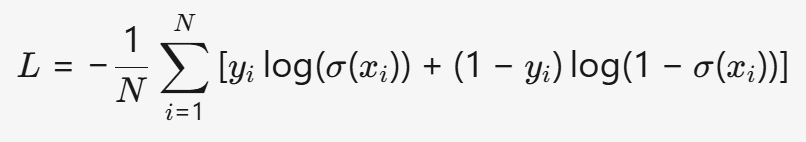
- 特点:
- 内部集成Sigmoid，数值更稳定。
- 适合输出未归一化的logits。
- 适用场景:
- 二分类任务（默认选择，优于BCELoss）。
(4) CrossEntropyLoss
- 公式:
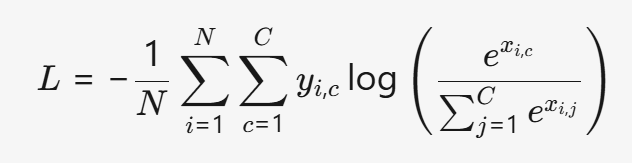
- 特点:
- 内部集成Softmax和NLLLoss。
- 直接处理原始logits，无需手动归一化。
- 适用场景:
- 多分类任务（如ResNet、ViT）。
(5) MultiLabelSoftMarginLoss
- 公式:
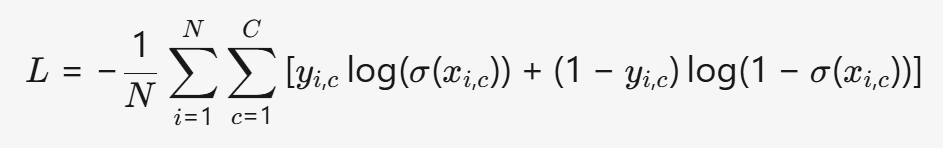
- 特点:
- 允许一个样本属于多个类别（多标签分类）。
- 输出为每个类别的概率（0到1之间）。
- 适用场景:
- 多标签分类（如图像中同时包含猫和狗）。
3. 其他损失函数
(1) HingeEmbeddingLoss (用于半监督/度量学习)
- 公式:
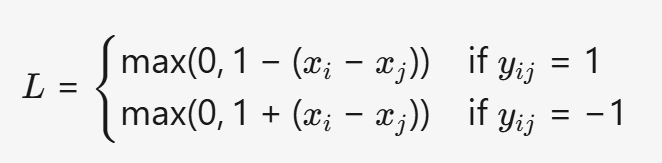
- 特点:
- 鼓励相似样本靠近，不相似样本远离。
- 常用于Siamese网络（如人脸验证）。
(2) TripletLoss (用于度量学习)
- 公式:
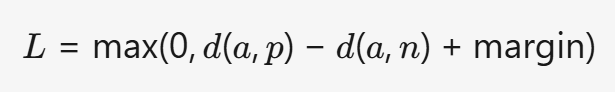（d为距离，a为锚点，p为正样本，n为负样本） - 适用场景:
- 需要学习特征嵌入的任务（如FaceNet人脸识别）。
(3) CTCLoss (Connectionist Temporal Classification)
- 特点:
- 无需对齐输入输出序列（如语音识别）。
- 处理不定长序列数据。
- 适用场景:
- 序列标注任务（如OCR文字识别）。
以下是更详细的 PyTorch 损失函数解析，涵盖数学公式、适用场景、优缺点对比及代码示例：
1. 回归损失函数（Regression Losses）
(1) L1Loss (Mean Absolute Error, MAE)
- 公式:L=N1i=1∑N∣yi−y^i∣
- 特点:
- 对异常值鲁棒（因为绝对值函数梯度恒定）。
- 梯度不随误差大小变化，可能导致收敛慢。
- 适用场景:
- 目标变量存在异常值时（如房价预测）。
- 需要稳定梯度的场景。
(2) MSELoss (Mean Squared Error, MSE)
- 公式:L=N1i=1∑N(yi−y^i)2
- 特点:
- 对误差大的样本惩罚更重（平方放大了异常值影响）。
- 梯度随误差增大而增大，可能收敛更快。
- 适用场景:
- 数据干净且异常值较少时（如物理实验预测）。
- 需要强信号指导优化的任务。
(3) SmoothL1Loss
- 公式:L={0.5(x)2∣x∣−0.5if ∣x∣<1otherwise
- 特点:
- 结合MSE和L1的优点：小误差时平滑，大误差时鲁棒。
- 避免MSE的梯度爆炸问题。
- 适用场景:
- 目标检测中的边界框回归（如Faster R-CNN）。
- 需要平衡精度和鲁棒性的任务。
(4) HuberLoss (Smooth Mean Absolute Error)
- 公式:L={21(yi−y^i)2δ(∣yi−y^i∣−21δ)if ∣yi−y^i∣<δotherwise
- 特点:
- 可调节超参数δ控制鲁棒性。
- 比SmoothL1Loss更灵活。
- 适用场景:
- 需要动态调整鲁棒性的回归任务（如金融预测）。
(5) KLDivLoss (Kullback-Leibler Divergence)
- 公式:L=i=1∑Nyilog(y^iyi)
- 特点:
- 衡量两个概率分布的差异（非对称）。
- 常用于生成模型（如GANs、VAEs）。
- 适用场景:
- 概率分布对齐（如文本生成、图像生成）。
2. 分类损失函数（Classification Losses）
(1) NLLLoss (Negative Log-Likelihood)
- 公式:L=−N1i=1∑Nlog(y^i,c)（y^i,c是样本i属于类别c的概率）
- 特点:
- 要求输入是log概率（通常配合LogSoftmax使用）。
- 数值稳定（避免log(0)问题）。
- 适用场景:
- 多分类任务（如图像分类）。
(2) BCELoss (Binary Cross-Entropy)
- 公式:L=−N1i=1∑N[yilog(y^i)+(1−yi)log(1−y^i)]
- 特点:
- 直接处理0-1概率输出（需配合Sigmoid）。
- 对类别不平衡敏感。
- 适用场景:
- 二分类任务（如垃圾邮件检测）。
(3) BCEWithLogitsLoss
- 公式:L=−N1i=1∑N[yilog(σ(xi))+(1−yi)log(1−σ(xi))]（σ(xi)是Sigmoid函数）
- 特点:
- 内部集成Sigmoid，数值更稳定。
- 适合输出未归一化的logits。
- 适用场景:
- 二分类任务（默认选择，优于BCELoss）。
(4) CrossEntropyLoss
- 公式:L=−N1i=1∑Nc=1∑Cyi,clog(∑j=1Cexi,jexi,c)
- 特点:
- 内部集成Softmax和NLLLoss。
- 直接处理原始logits，无需手动归一化。
- 适用场景:
- 多分类任务（如ResNet、ViT）。
(5) MultiLabelSoftMarginLoss
- 公式:L=−N1i=1∑Nc=1∑C[yi,clog(σ(xi,c))+(1−yi,c)log(1−σ(xi,c))]
- 特点:
- 允许一个样本属于多个类别（多标签分类）。
- 输出为每个类别的概率（0到1之间）。
- 适用场景:
- 多标签分类（如图像中同时包含猫和狗）。
3. 其他损失函数
(1) HingeEmbeddingLoss (用于半监督/度量学习)
- 公式:L={max(0,1−(xi−xj))max(0,1+(xi−xj))if yij=1if yij=−1
- 特点:
- 鼓励相似样本靠近，不相似样本远离。
- 常用于Siamese网络（如人脸验证）。
(2) TripletLoss (用于度量学习)
- 公式:L=max(0,d(a,p)−d(a,n)+margin)（d为距离，a为锚点，p为正样本，n为负样本）
- 适用场景:
- 需要学习特征嵌入的任务（如FaceNet人脸识别）。
(3) CTCLoss (Connectionist Temporal Classification)
- 特点:
- 无需对齐输入输出序列（如语音识别）。
- 处理不定长序列数据。
- 适用场景:
- 序列标注任务（如OCR文字识别）。
如何选择损失函数？
| 任务类型 | 推荐损失函数 | 原因 |
|---|---|---|
| 回归（鲁棒性） | SmoothL1Loss/HuberLoss | 对异常值不敏感 |
| 回归（精度） | MSELoss | 误差大时梯度大，收敛快 |
| 二分类 | BCEWithLogitsLoss | 数值稳定，集成Sigmoid |
| 多分类 | CrossEntropyLoss | 直接处理logits，避免手动Softmax |
| 多标签分类 | MultiLabelSoftMarginLoss | 允许样本属于多个类别 |
| 度量学习 | TripletLoss/HingeLoss | 学习样本间相似性 |
| 序列标注 | CTCLoss | 处理不定长序列 |