控制建模matlab练习15:线性状态反馈控制器-④最优化控制LQR
此练习,主要是使用状态空间方程来设计控制器的方法和思路:
①系统建模;
②系统的能控性;
③极点配置;
④最优化控制LQR;
⑤轨迹追踪;
以下是,第④部分:最优化控制LQR;
一、LQR控制器的介绍
- 在设计反馈控制 K 的时候,如何选择闭环状态矩阵的特征值涉及最优控制,以基础的最优控制器-LQR控制器为例。
- LQR全称为Linear Quadratic Regulator ,就是线性二次型调节器。
- 同样,基于前面的系统建模和极点配置的内容:
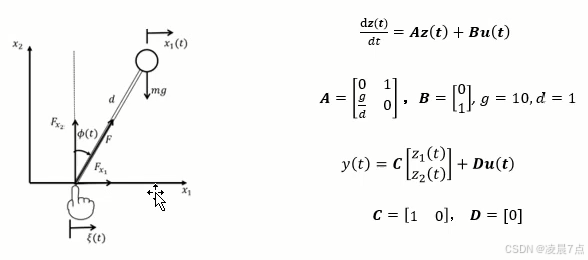

二、LQR控制器的思路
- 由之前练习,当使用线性状态反馈控制时,令 u(t) = -Kz(t) ,可以得到闭环控制系统的状态空间方程 (A - BK)z(t) = Aclz(t) ;
- 此时,通过设计不同的 K 值可以改变闭环状态矩阵 Acl 的特征值。
- 为了选择更好的选择特征值,引入代价函数。
J=∫0∞z(t)TQz(t)+u(t)TRu(t)dt . J = \int_0^\infty z(t)^{T}Qz(t)+u(t)^{T}Ru(t)dt\,. J=∫0∞z(t)TQz(t)+u(t)TRu(t)dt. - 控制器设计的目的,选择合适的 K 值,从而得到代价函数 J 的最小值 Jmin 。
- 一般情况, Q 、 R 会选择对角矩阵,且对角线上的元素都大于0。
三、LQR控制器的设计
- 其实,这个控制器的设计和上一个练习一样,就是在做极点配置;但前面的 K 是随机选择的,而LQR是根据权重系数来选择。
- 以下有三组权重矩阵系数:
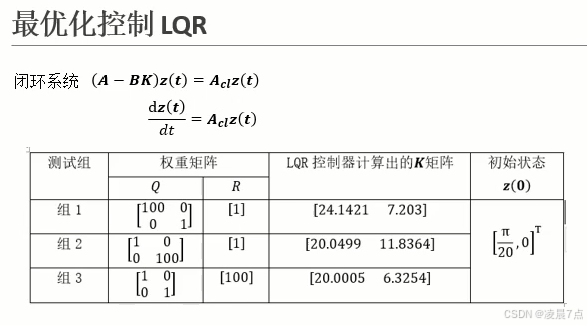
- 组1:Q=[100001]Q=\begin{bmatrix} 100 & 0 \\ 0 & 1 \\ \end{bmatrix}Q=[100001]、R=[1]R=\begin{bmatrix} 1 \end{bmatrix}R=[1],此时更看重状态变量 z1(t) 的收敛速度。
- 组2:Q=[100100]Q=\begin{bmatrix} 1 & 0 \\ 0 & 100 \\ \end{bmatrix}Q=[100100]、R=[1]R=\begin{bmatrix} 1 \end{bmatrix}R=[1],此时更看重状态变量 z2(t) 的收敛速度。
- 组3:Q=[1001]Q=\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}Q=[1001]、R=[100]R=\begin{bmatrix} 100 \end{bmatrix}R=[100],此时更看重输入 u 的能耗。
- 在MATLAB中的代码实现如下:
- 其中,例如,[K1, z, l] = lqr (sys, q1, r1);%%这里用的lqr的语句,其输入输出是:
- sys: 输入,当前的系统;
- q1: 输入,当前Q矩阵;
- r1: 输入,当前R矩阵;
- K1: 输出,所要求设计的K矩阵;
- z: 输出,状态变量;
- l: 输出,代表极点;
clc;clear;close all;
%% 定义参数g=10;d=1;
%% 定义矩阵A=[0 1;g/d 0];B=[0;1];C = [1, 0];D = 0;
%% 建立状态空间方程表达式
sys = ss(A,B,C,D);
%% 定义初始状态
z0=[pi/20;0];%% 定义权重系数,求K
q1=[100 0;0 1];
r1=1;
[K1, z, l] = lqr (sys, q1, r1);q2=[1 0;0 100];
r2=1;
[K2, z, l] = lqr (sys, q2, r2);q3=[1 0;0 1];
r3=100;
[K3, z, l] = lqr (sys, q3, r3);%% 定义闭环系统
sys_cl1=ss(A-B*K1,[0;0],C,D);
sys_cl2=ss(A-B*K2,[0;0],C,D);
sys_cl3=ss(A-B*K3,[0;0],C,D);%% 仿真
%% 对初始条件的响应
t=0:0.01:5;
[y1,t,z1]=initial(sys_cl1,z0,t);
[y2,t,z2]=initial(sys_cl2,z0,t);
[y3,t,z3]=initial(sys_cl3,z0,t);%% 绘图
%% 状态变量1
subplot(3,1,1);
plot(t,z1(:,1));
hold on;
plot(t,z2(:,1));
hold on;
plot(t,z3(:,1));
legend('z1_1','z1_2','z1_3');
grid on;
hold off;
title('状态变量z1的变化曲线')
legend('组1权重矩阵z1_1','组2权重矩阵z1_2','组3权重矩阵z1_3')
z1_1 = sum (z1(:,1).^2) %%加这个.,就是第一列所有元素,自己跟自己平方的加和。如果没有这个.,就是矩阵相乘了。
z1_2 = sum (z2(:,1).^2)
z1_3 = sum (z3(:,1).^2)%% 状态变量2
subplot(3,1,2);
plot(t,z1(:,2));
hold on;
plot(t,z2(:,2));
hold on;
plot(t,z3(:,2));
legend('z2_1','z2_2','z2_3');
grid on;
hold off;
title('状态变量z2的变化曲线')
legend('组1权重矩阵z2_1','组2权重矩阵z2_2','组3权重矩阵z2_3')
z2_1 = sum (z1(:,2).^2)
z2_2 = sum (z2(:,2).^2)
z2_3 = sum (z1(:,2).^2)%% 系统输入
subplot(3,1,3);
plot(t,-K1*z1');
hold on;
plot(t,-K2*z3');
hold on;
plot(t,-K3*z3');
legend('u_1','u_2','u_3');
grid on;
hold off;
title('输入变量u的变化曲线')
legend('组1权重矩阵u_1','组2权重矩阵u_2','组3权重矩阵u_3')
u_1 = sum ((-K1*z1').^2)
u_2 = sum ((-K2*z2').^2)
u_3 = sum ((-K3*z3').^2)四、运行结果
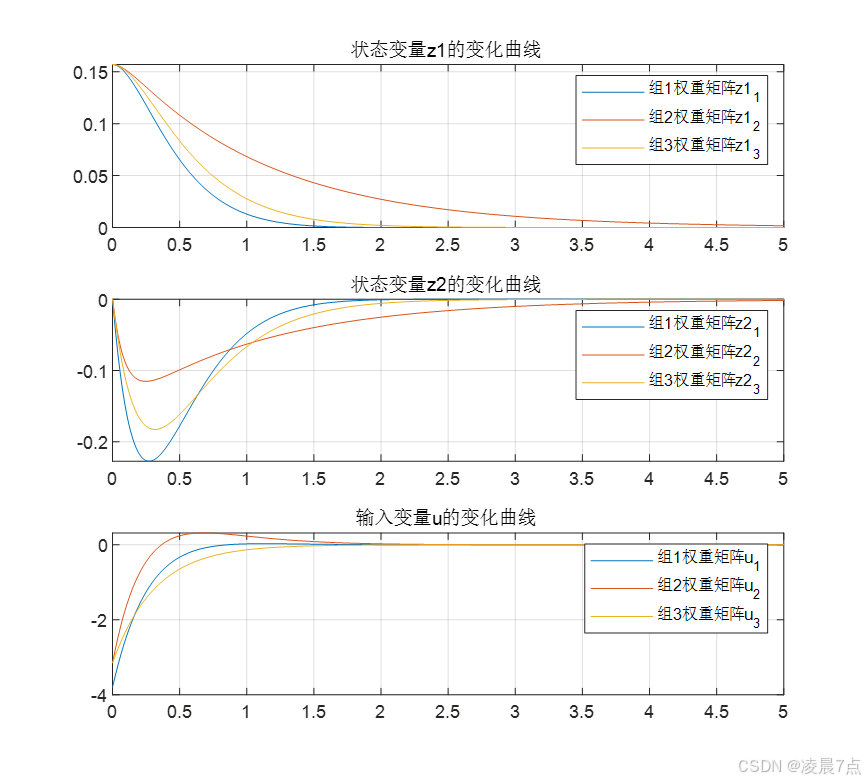
- 在状态变量 z1(t) 变化曲线,可以看出在组1权重系数矩阵Q=[100001]Q=\begin{bmatrix} 100 & 0 \\ 0 & 1 \\ \end{bmatrix}Q=[100001]、R=[1]R=\begin{bmatrix} 1 \end{bmatrix}R=[1],是收敛最快的,因为从Q矩阵的100看出其更注重 z1(t) 的收敛速度;
- 在状态变量 z2(t) 变化曲线,可以看出在组2权重系数矩阵Q=[100100]Q=\begin{bmatrix} 1 & 0 \\ 0 & 100 \\ \end{bmatrix}Q=[100100]、R=[1]R=\begin{bmatrix} 1 \end{bmatrix}R=[1],是收敛最快的,因为从Q矩阵的100看出其更注重 z2(t) 的收敛速度;
- 在输入 u 变化曲线,可以看出在组3权重系数矩阵Q=[1001]Q=\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}Q=[1001]、R=[100]R=\begin{bmatrix} 100 \end{bmatrix}R=[100],是收敛最快的,因为从R矩阵的100看出其更注重输入 u 有最小的能耗的;
- 同时可以在命令行窗口,定量计算了不同权重系数矩阵下,对系统的不同影响(如下图运行的结果);

- 对于状态变量 z1(t) ,在组1权重系数矩阵,其输出结果的平方加和是0.8005最小的,也就说明在组1情况是最快收敛到0的;
- 对于状态变量 z2(t) ,在组2权重系数矩阵,其输出结果的平方加和是1.0474最小的,也就说明在组2情况是最快收敛到0的;
- 对于输入 u ,在组3权重系数矩阵,其输出结果的平方加和是161.0392最小的,也就说明在组3情况是最快收敛到0的;
- 结果总结:
- 从 z1(t) 收敛,可以说组1的设计结果是好的;
- 但从 z2(t) 收敛,也可以说组2的设计结果是好的;
- 但从输入 u 的能耗角度来看,也可以说组3的设计结果是好的;
学习来源:《控制之美》[卷1],王天威
