环形子数组的最大和

问题描述与解题思路

题目链接

这个题的特殊之处就在于它子数组的选取方式，比如[1,2,3,4]这个数组
，我们以3为子数组的起点，子数组的选取情况如下：

• 3
• 3 4
• 3 4 1
• 3 4 1 2

那么对于本题的解题方式，我们依然是要通过分类讨论，将这个环形数组的问题转化成我们普通最大子数组的问题来求和（就和打家劫舍2那道题目的思路是一样的）

看下面这张图，如果我们遍历到的子数组是我们的普通情况，那就按照我们之前处理过的模板来解决。如果我们遍历到的子数组是这种头一段尾一段的情况。那也很好办，因为它的补集——中间的这个数组就属于我们的普通情况，我们要求外面这个数组的最大和，只需要求中间这个数组的最小和就行了，求出来之后拿整个数组的和一减就能得到我们要的结果。

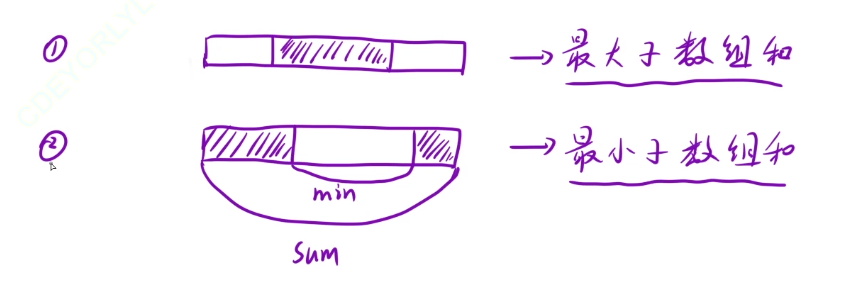
确定本题的状态表示

通过上面的分析，我们已经讲一个环形子数组和问题转化成了一个普通的子数组和问题，然后我们后面去求f[i]的时候就不用考虑那种分布在两头的子树组了（比如 对于[0 1 2 3 ]求 f[1]，你不用考虑以1为尾，以3为首的子数组，因为这种情况自有我们的g数组来去处理，你在进行动态规划填充的时候仍然只需要老老实实的做你的普通数组问题即可）

确定本题的状态转移方程

初始化

返回值

整体思路就是找到f数组里面的最大值。以及g数组里面的最小值，比较出max(f_max，sum - g_min)，但是这里还需要考虑一种特殊情况，就是你数组里面的数全是负数。

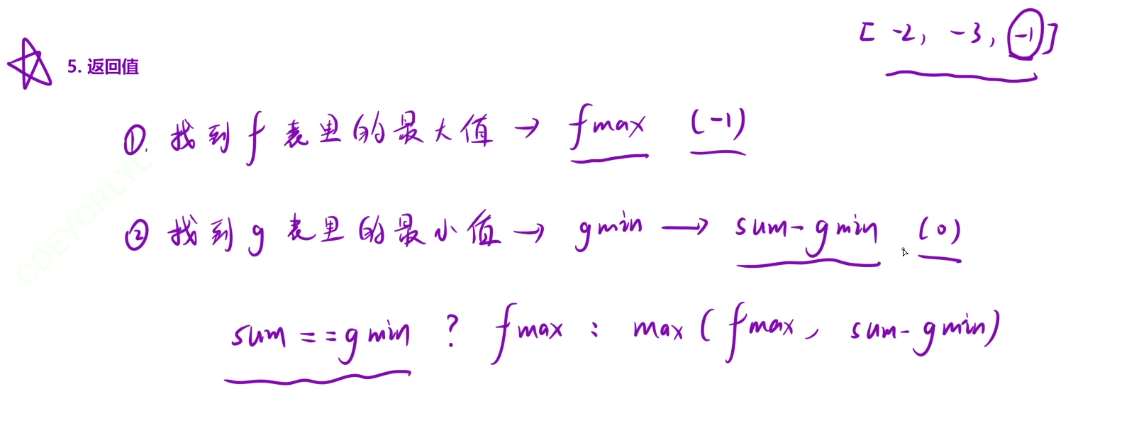
代码实现

int maxSubarraySumCircular(vector<int>& nums)
{// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回结果int n = nums.size();vector<int> f(n + 1), g(n + 1);int fmax = INT_MIN, gmin = INT_MAX, sum = 0;for(int i = 1; i <= n; i++){int x = nums[i - 1];f[i] = max(x, x + f[i - 1]);fmax = max(fmax, f[i]);g[i] = min(x, x + g[i - 1]);gmin = min(gmin, g[i]);sum += x;}return sum == gmin ? fmax : max(fmax, sum - gmin);
}