当前位置：首页 > news >正文

代码随想录Day58：图论（拓扑排序精讲、最短路算法dijkstra朴素版精讲）

news 2025/8/22 10:35:59

一、实战

拓扑排序精讲

117. 软件构建

拓扑排序不是排序，是经典的图论问题。拓扑排序在文件处理上也有应用，我们在做项目安装文件包的时候，经常发现复杂的文件依赖关系， A依赖B，B依赖C，B依赖D，C依赖E 等等。当然拓扑排序也要检测这个有向图是否有环，即存在循环依赖的情况，因为这种情况是不能做线性排序的。

由此我们推断出拓扑排序的应用场景：任务调度、依赖排序问题（比如编译顺序、课程先修）

给出一个有向图，把这个有向图转成线性的排序
图论中判断有向无环图的常用方法

拓扑排序的思路：拓扑排序指的是一种解决问题的大体思路，而具体算法，可能是广搜也可能是深搜。实现拓扑排序的算法有两种：卡恩算法（基于入度的 BFS）和DFS。这里我们选择相对清晰易懂的BFS实现思路。

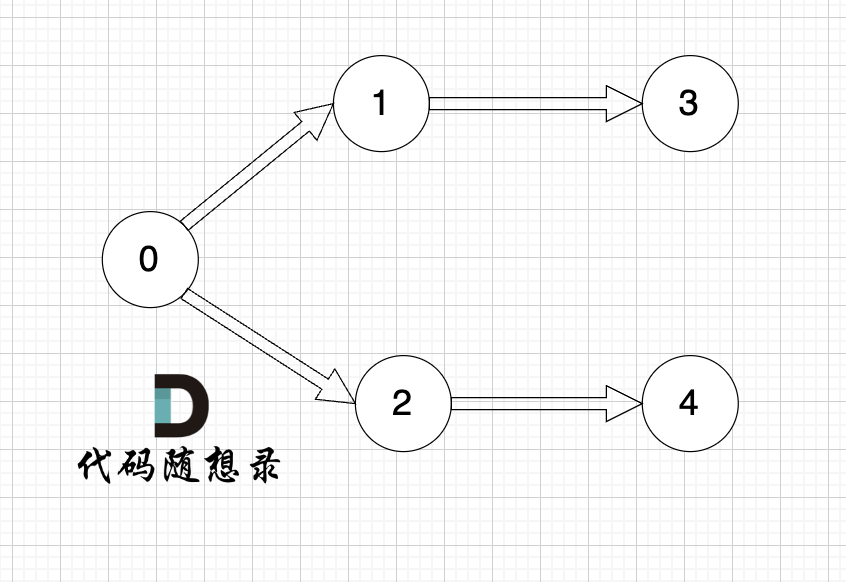
本图的出发节点特征**入度为0 出度为2**，也就是没有边指向它，而它有两条边是指出去的

所以当我们做拓扑排序的时候，应该优先找入度为 0 的节点，只有入度为0，它才是出发节点。

拓扑排序的过程，其实就循环两步：

找到入度为0 的节点，加入结果集
将该节点从图中移除

模拟过程：

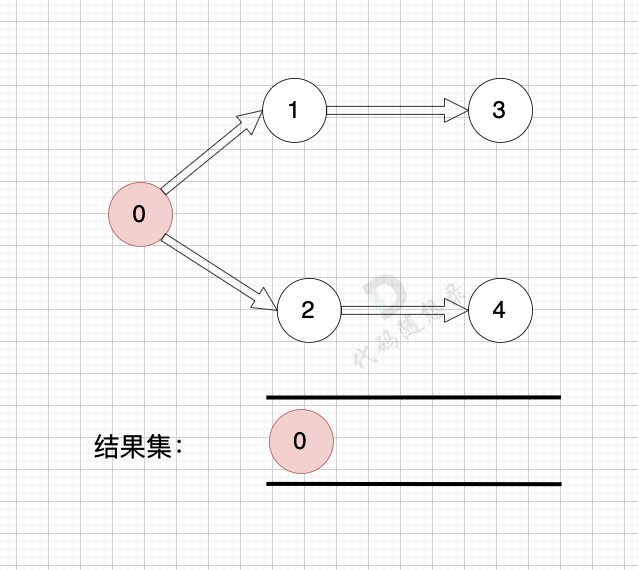
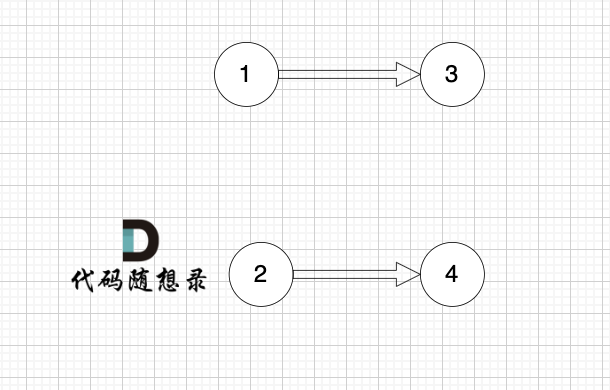
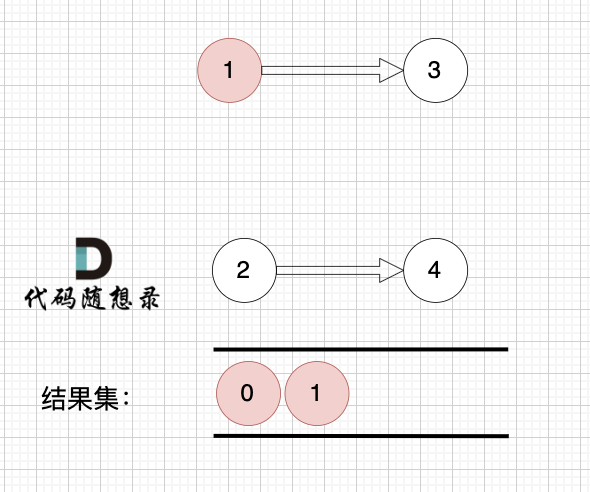
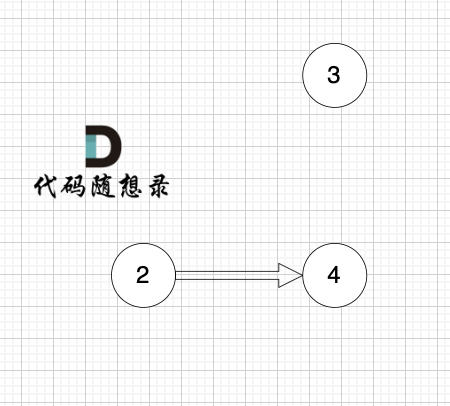
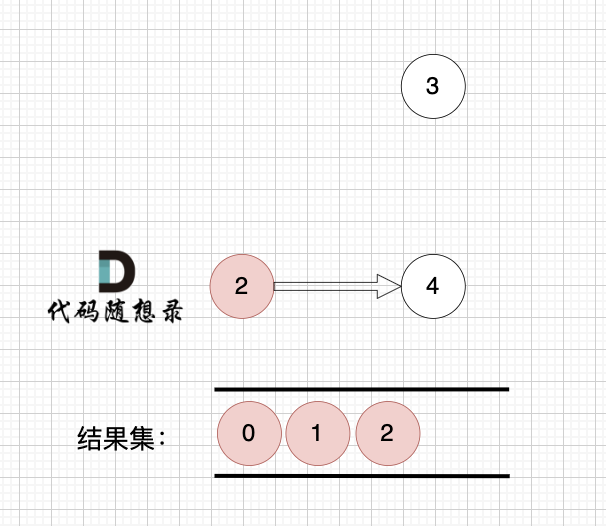
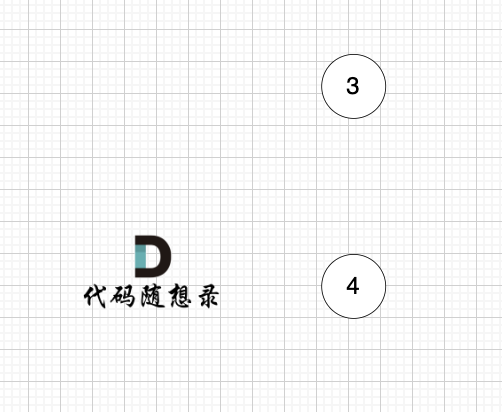
找到入度为0 的节点，加入结果集。节点1 和节点2 入度都为0，选哪个都行，所以这也是为什么拓扑排序的结果是不唯一的。

最后结果集为： 0 1 2 3 4 。当然结果不唯一。

如何判断有环？

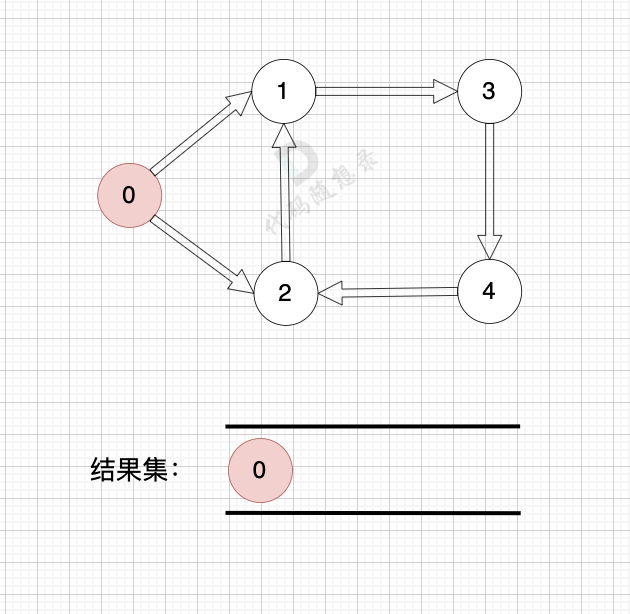
节点0 接入结果集之后，节点1、2、3、4 形成了环，找不到入度为0 的节点了，所以此时结果集里只有一个元素。那么如果我们发现结果集元素个数不等于图中节点个数，我们就可以认定图中一定有有向环！

package org.example;//运行时去掉import java.util.*;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(); // 顶点数（文件数量）int m = scanner.nextInt(); // 边数（依赖关系数量）// 邻接表：map.get(i) 表示节点 i 指向的所有节点列表List<List<Integer>> map = new ArrayList<>();int[] in = new int[n]; // 入度数组：in[i] 表示有多少条边指向节点 i// 初始化邻接表：为每个节点创建一个空的邻接列表for (int i = 0; i < n; i++) {map.add(new ArrayList<>());}// 读入 m 条有向边for (int i = 0; i < m; i++) {int s = scanner.nextInt(); // 起点int t = scanner.nextInt(); // 终点map.get(s).add(t);         // 添加边 s → tin[t]++;                   // t 的入度加1（被指向一次）}// 创建队列，用于存储当前入度为0的节点（可执行的文件）Queue<Integer> queue = new LinkedList<>();// 将所有入度为0的节点加入队列（作为拓扑排序的起点）for (int i = 0; i < n; i++) {if (in[i] == 0) {queue.add(i);}}List<Integer> result = new ArrayList<>(); // 存储拓扑排序结果// 拓扑排序核心：BFS（广度优先搜索）过程while (!queue.isEmpty()) {int cur = queue.poll();        // 取出一个入度为0的节点result.add(cur);               // 将该节点加入结果序列// 遍历 cur 指向的所有邻居节点for (int k : map.get(cur)) {in[k]--;                   // 断开 cur → k 的边，k 的入度减1if (in[k] == 0) {          // 如果 k 的入度变为0queue.add(k);          // 加入队列，等待处理}}}// 检查是否所有节点都被排序if (result.size() == n) {// 输出拓扑排序结果（空格分隔）for (int i = 0; i < result.size(); i++) {System.out.print(result.get(i));if (i < result.size() - 1) {System.out.print(" ");}}} else {// 存在环，无法完成拓扑排序System.out.println(-1);}scanner.close(); // 关闭输入流（建议加上）}
}

最短路算法dijkstra朴素版精讲

47. 参加科学大会（第六期模拟笔试）

本题就是求最短路，最短路是图论中的经典问题即：给出一个有向图，一个起点，一个终点，问起点到终点的最短路径。

dijkstra算法：在有权图（权值非负数）中求从起点到其他节点的最短路径算法。

注意两点：

dijkstra 算法可以同时求起点到所有节点的最短路径
权值不能为负数（但是类似的Prim算法权值可以有负数）

dijkstra三部曲：

第一步，选源点到哪个节点近且该节点未被访问过
第二步，该最近节点被标记访问过
第三步，更新非访问节点到源点的距离（即更新minDist数组，minDist数组用来记录每一个节点距离源点的最小距离）

模拟过程：

初始化，minDist数组数值初始化为int最大值。

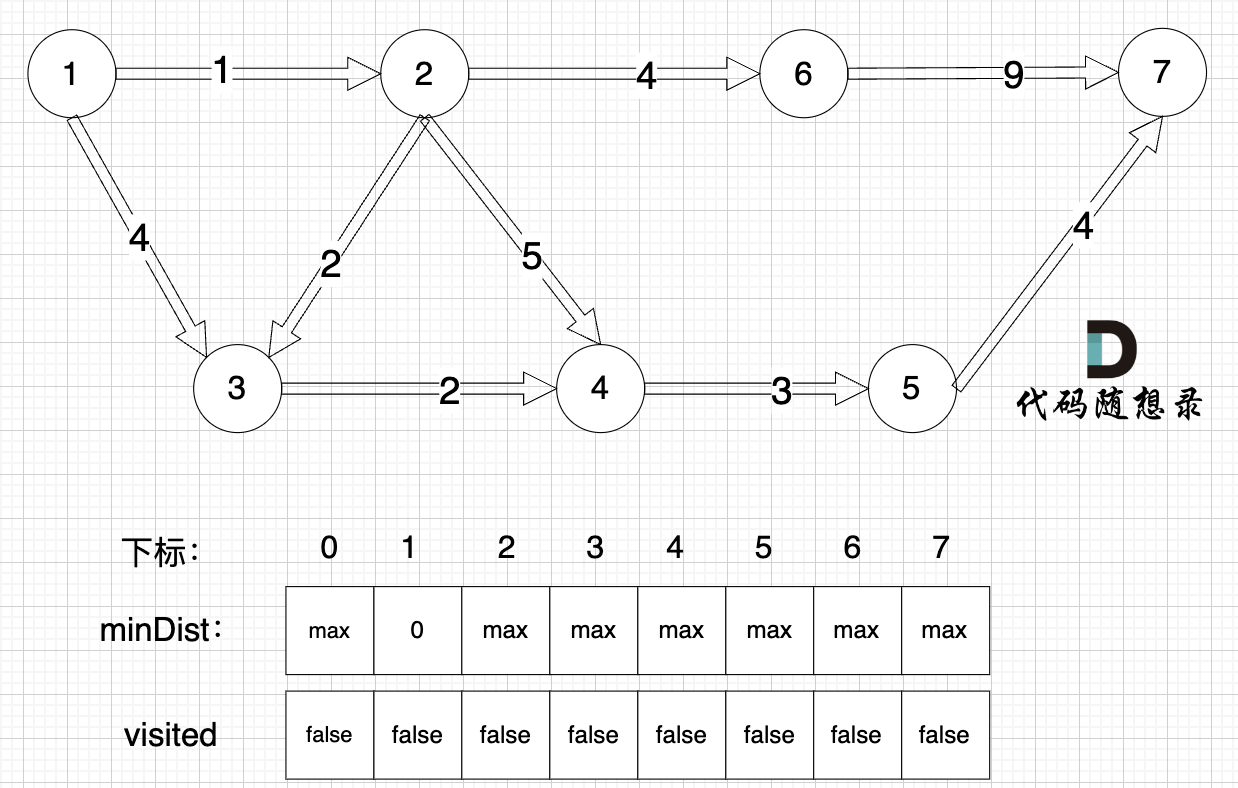
max 表示默认值，节点0 不做处理，统一从下标1 开始计算，这样下标和节点数值统一

开始循环三部曲

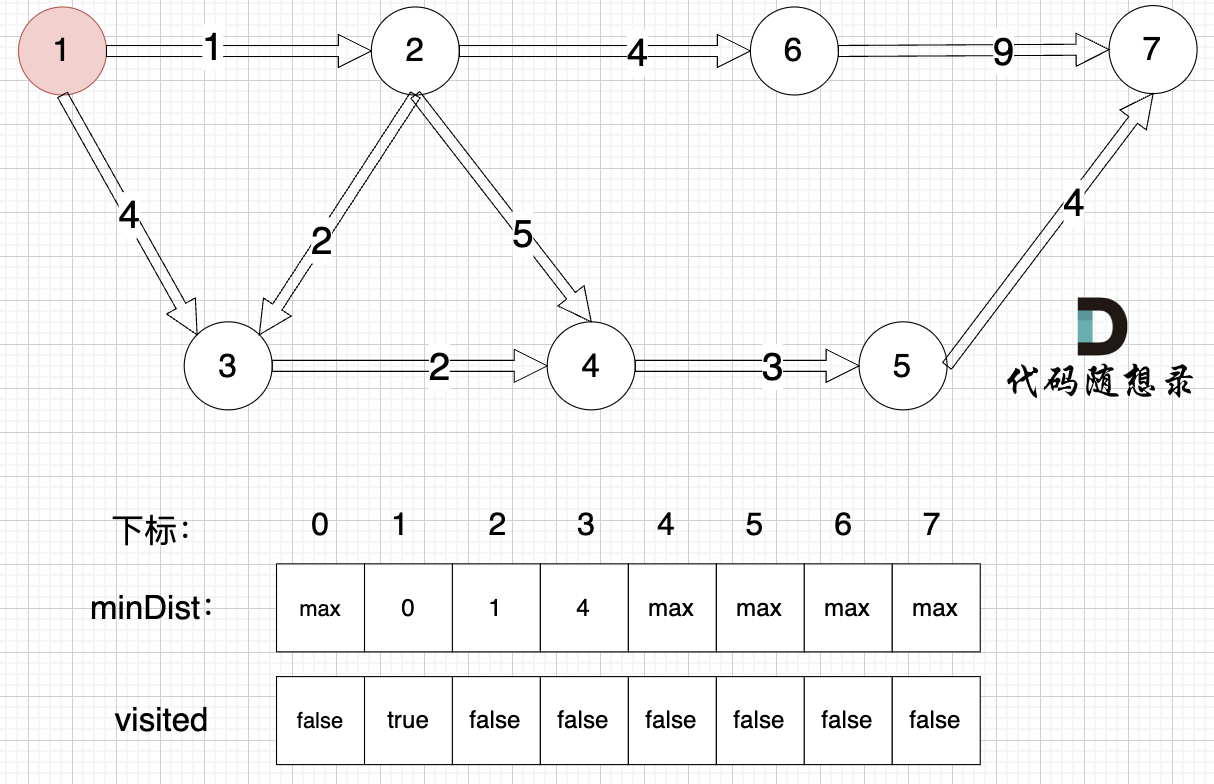
更新 minDist数组，即：源点（节点1）到节点2 和节点3的距离。

源点到节点2的最短距离为1，小于原minDist[2]的数值max，更新minDist[2] = 1
源点到节点3的最短距离为4，小于原minDist[3]的数值max，更新minDist[3] = 4

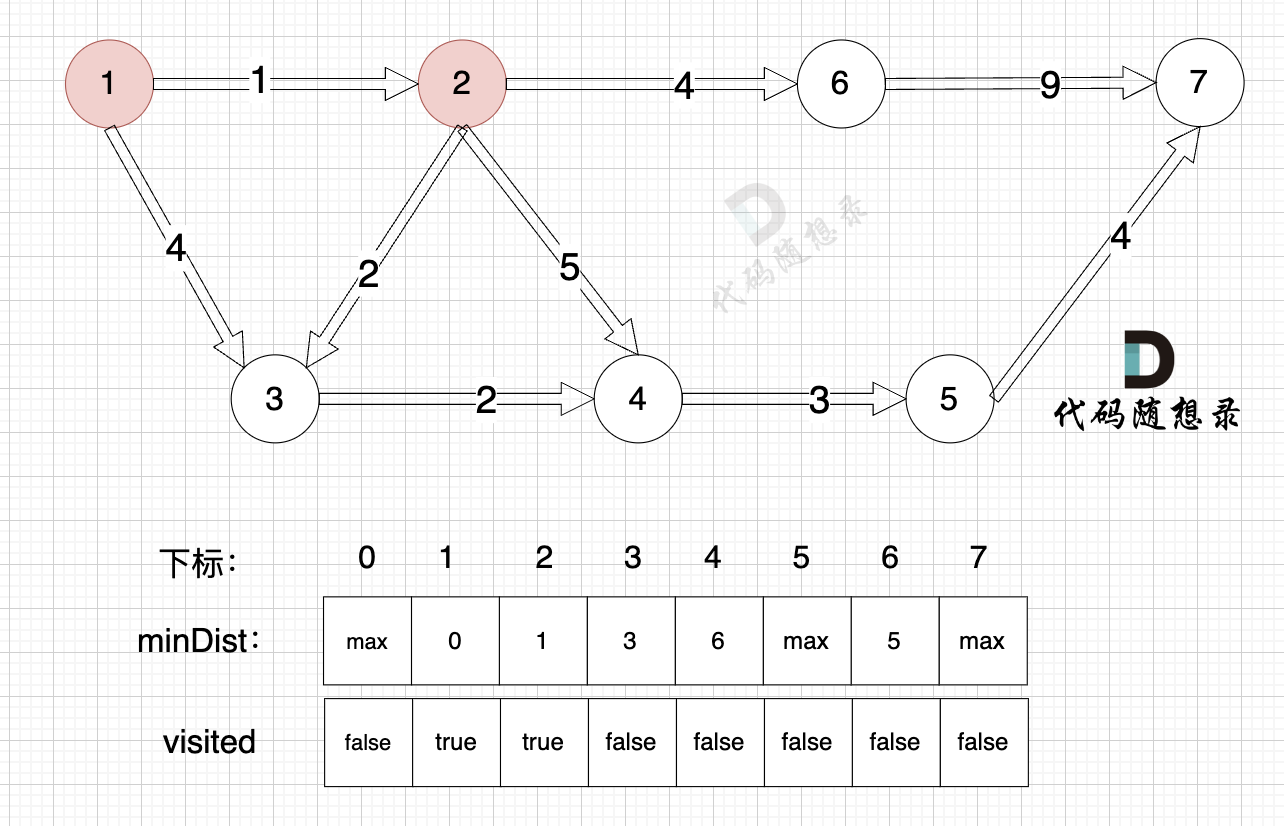
更新 minDist数组，即：源点（节点1）到节点6 、节点3 和节点4的距离。

更新 minDist数组：

源点到节点6的最短距离为5，小于原minDist[6]的数值max，更新minDist[6] = 5
源点到节点3的最短距离为3，小于原minDist[3]的数值4，更新minDist[3] = 3
源点到节点4的最短距离为6，小于原minDist[4]的数值max，更新minDist[4] = 6

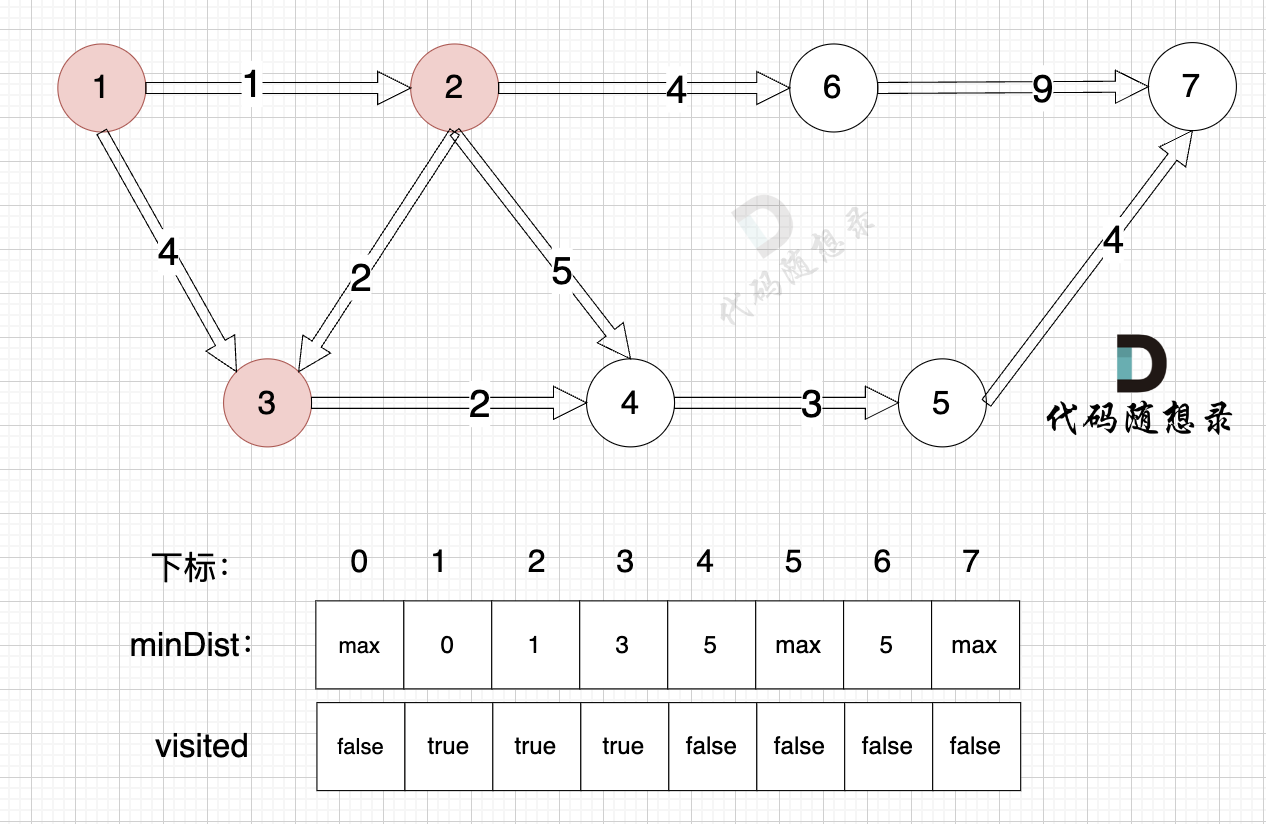
源点到节点4的最短距离为5，小于原minDist[4]的数值6，更新minDist[4] = 5

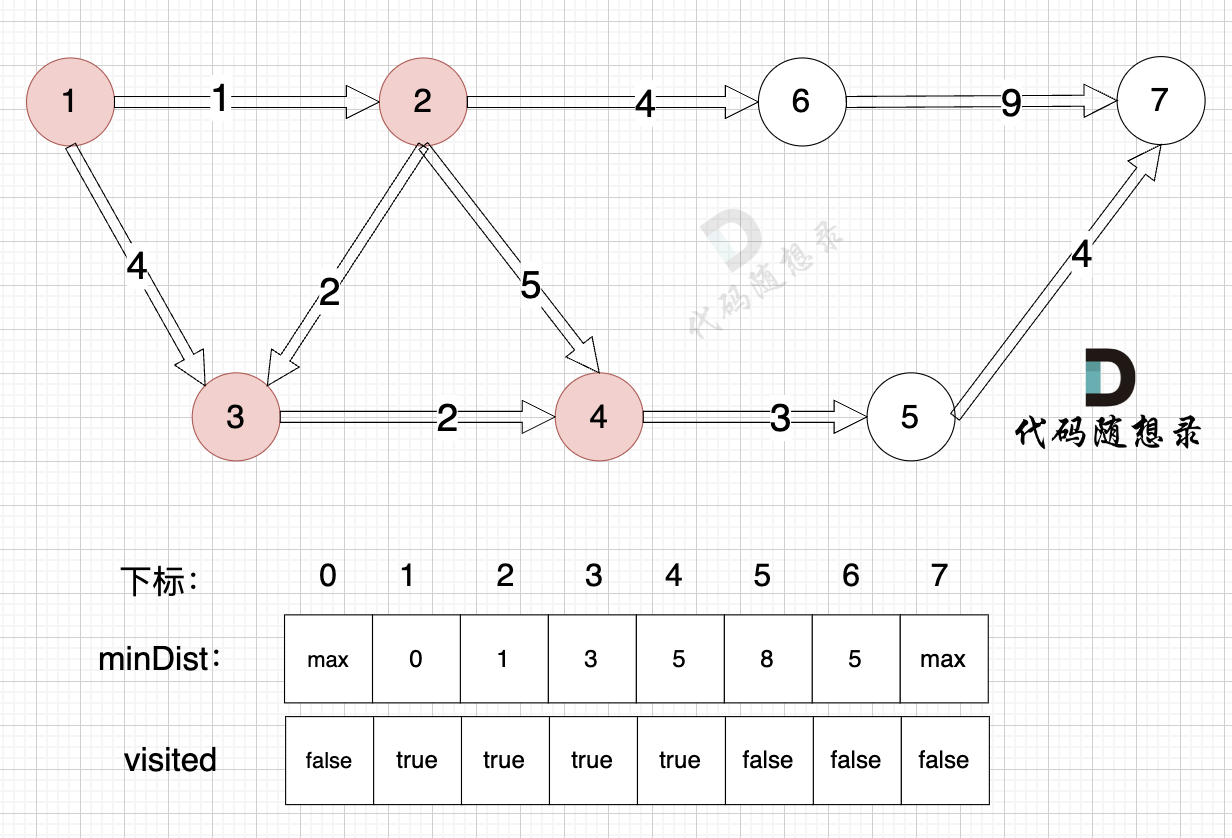
源点到节点5的最短距离为8，小于原minDist[5]的数值max，更新minDist[5] = 8

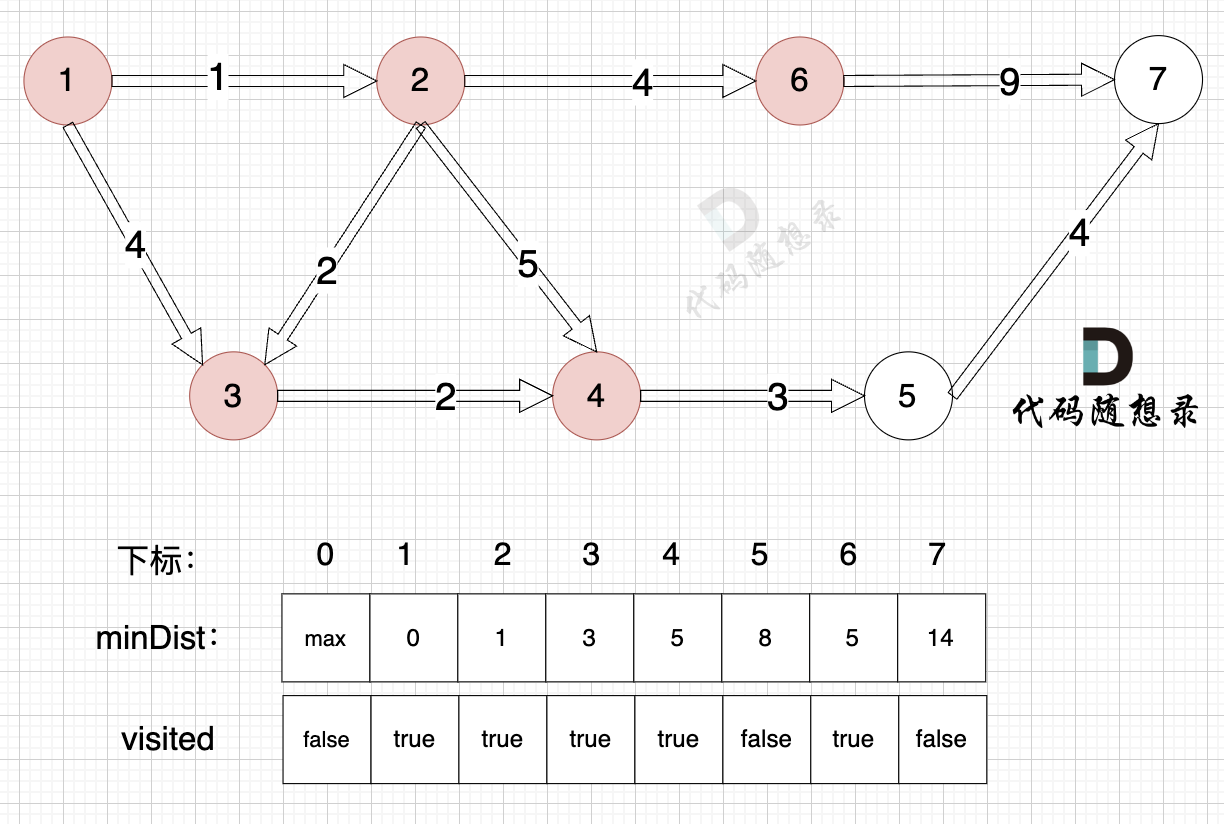
源点到节点7的最短距离为14，小于原minDist[7]的数值max，更新minDist[7] = 14

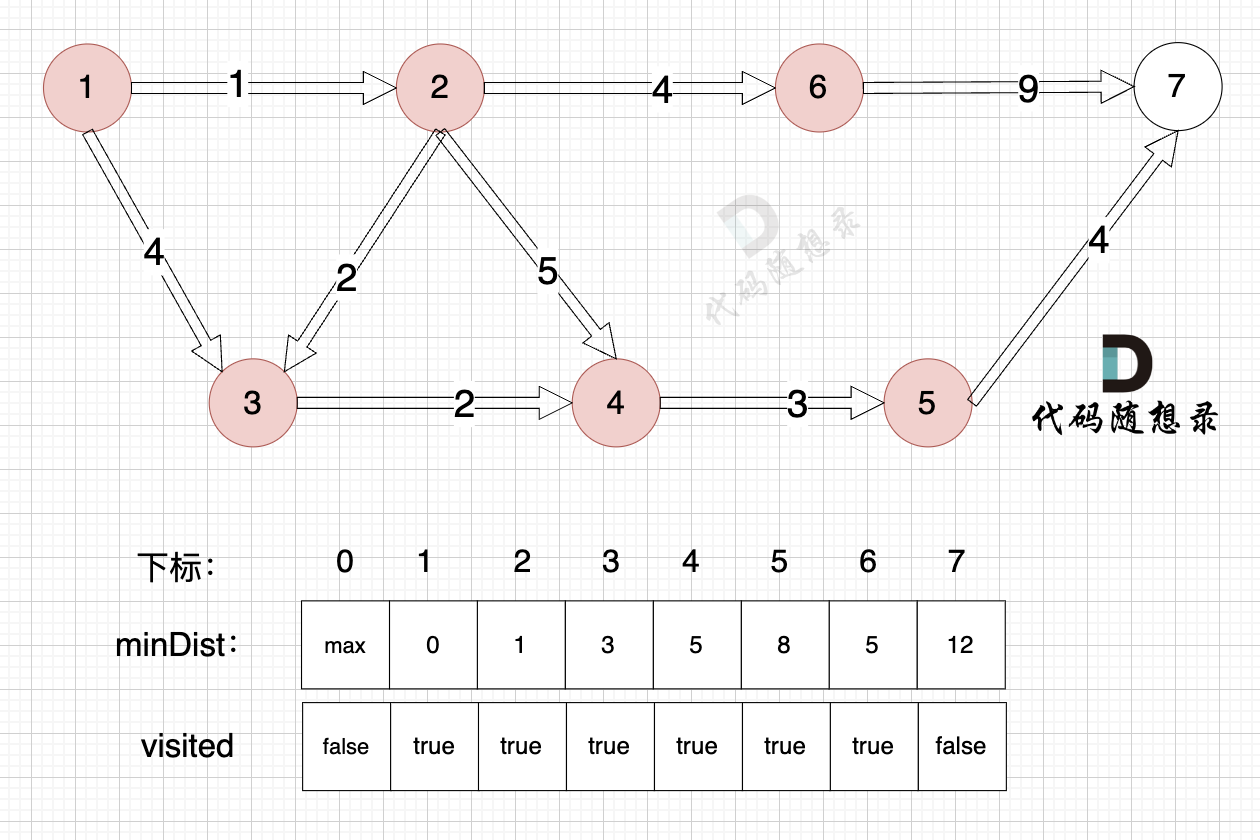
源点到节点7的最短距离为12，小于原minDist[7]的数值14，更新minDist[7] = 12

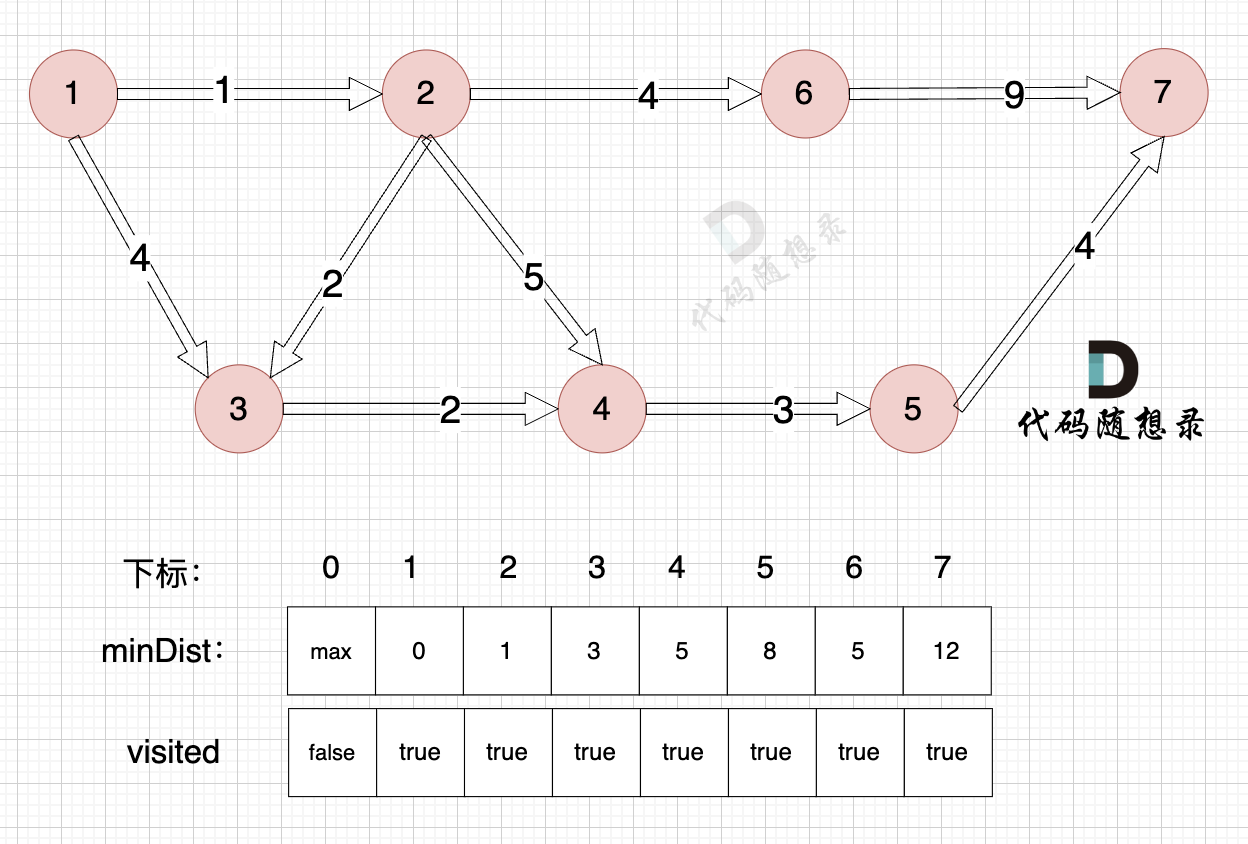
节点7加入，但节点7到节点7的距离为0，所以不用更新minDist数组

最后起点（节点1）到终点（节点7）的最短距离就是 minDist[7] ，按上面举例讲解来说，minDist[7] = 12，节点1 到节点7的最短路径为 12。

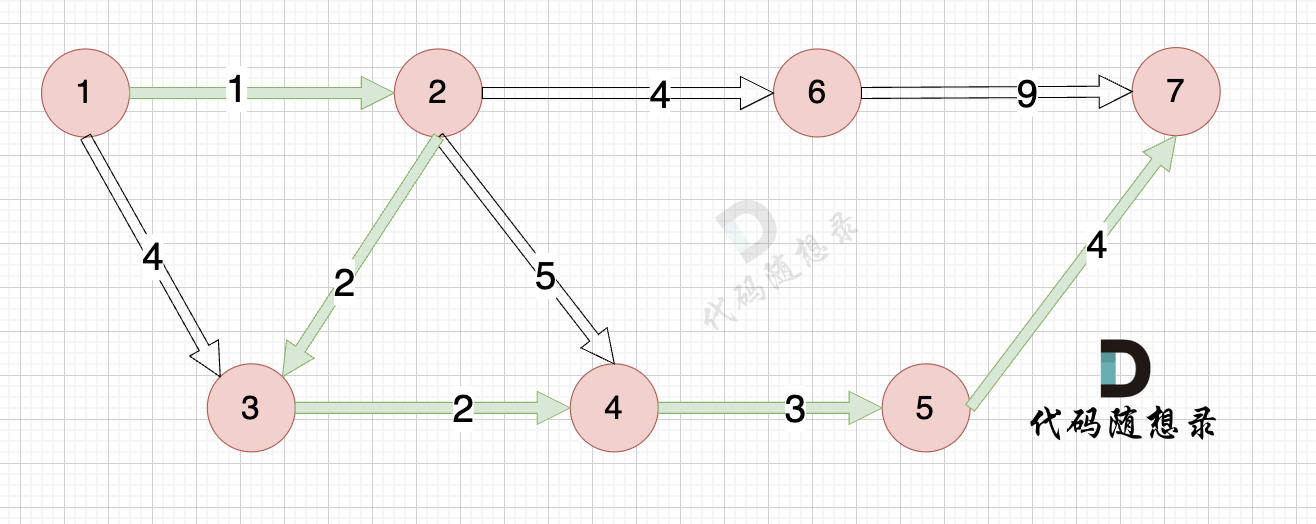
关于为什么dijkstra边的权值不能出现负数？

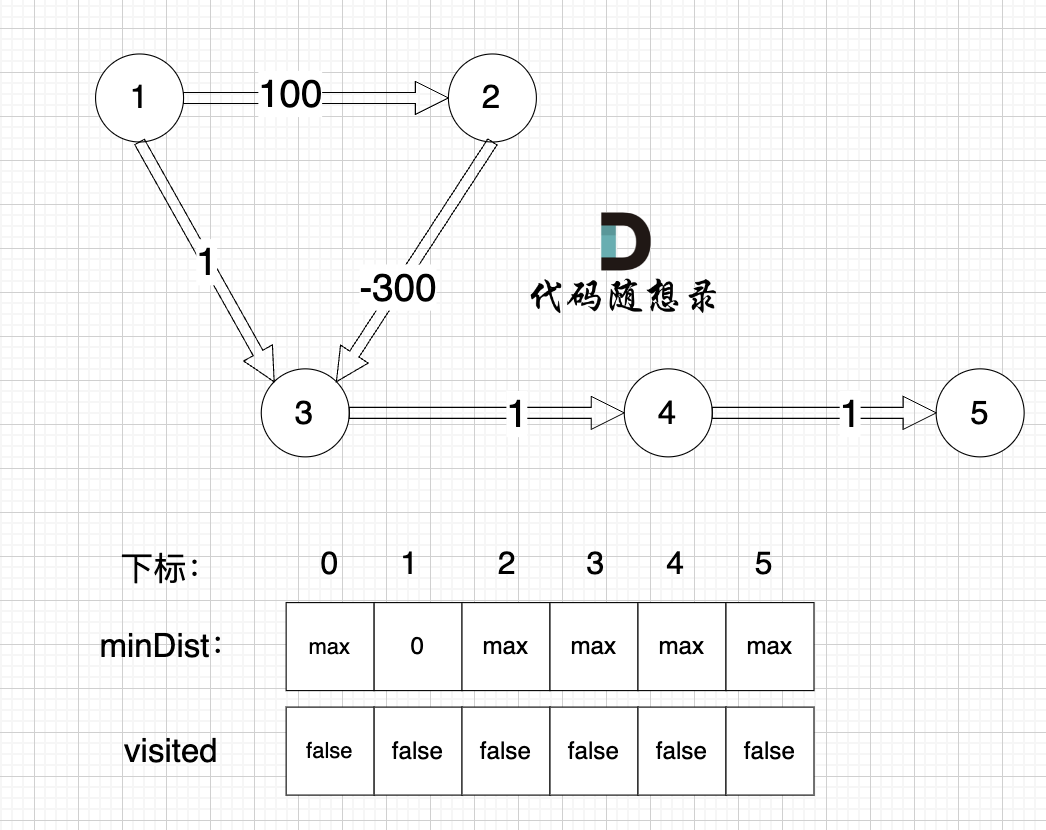
节点1 到节点5 的最短路径应该是节点1 -> 节点2 -> 节点3 -> 节点4 -> 节点5，继续dijkstra 三部曲来模拟

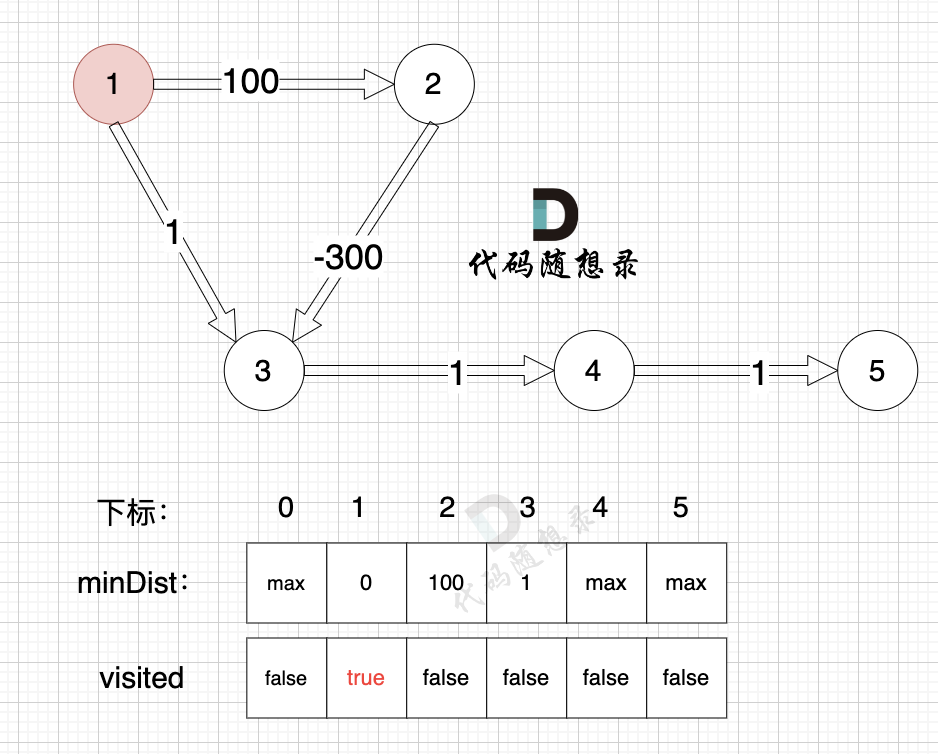
更新 minDist数组，即：源点（节点1）到节点2 和节点3的距离。

源点到节点2的最短距离为100，小于原minDist[2]的数值max，更新minDist[2] = 100
源点到节点3的最短距离为1，小于原minDist[3]的数值max，更新minDist[3] = 1

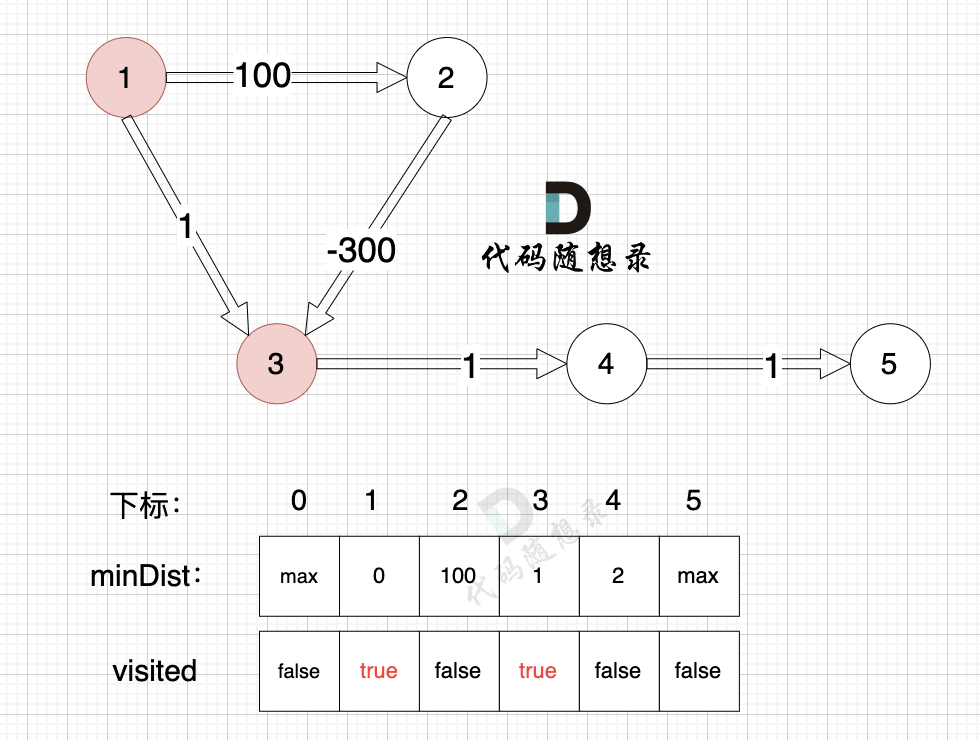
由于节点3的加入，那么源点可以有新的路径链接到节点4 所以更新minDist数组：

源点到节点4的最短距离为2，小于原minDist[4]的数值max，更新minDist[4] = 2

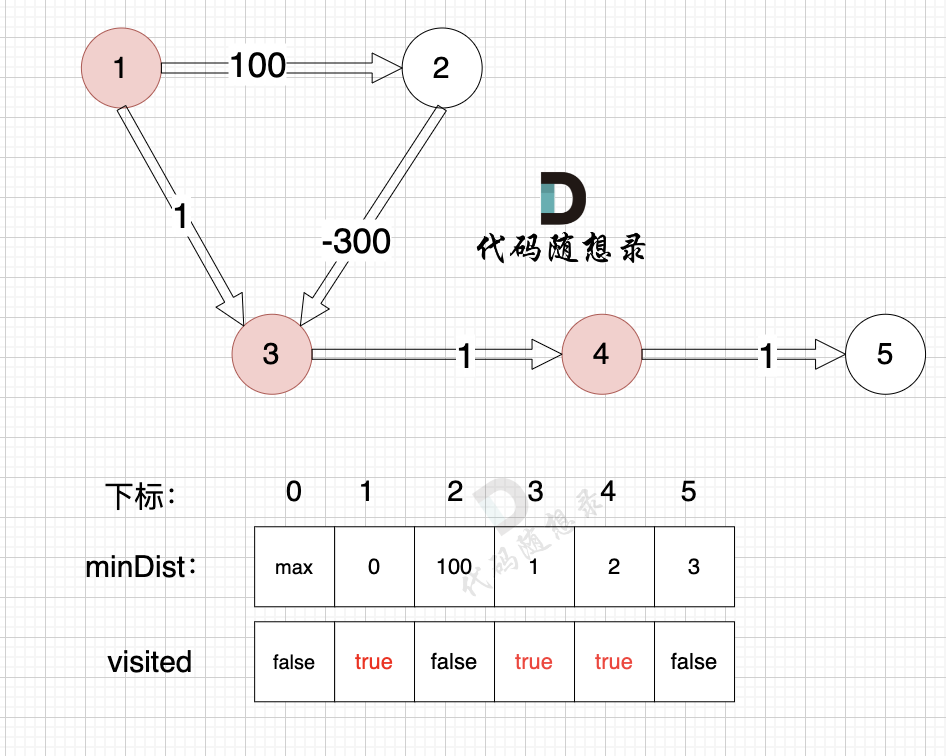
由于节点4的加入，那么源点可以有新的路径链接到节点5 所以更新minDist数组：

源点到节点5的最短距离为3，小于原minDist[5]的数值max，更新minDist[5] = 5

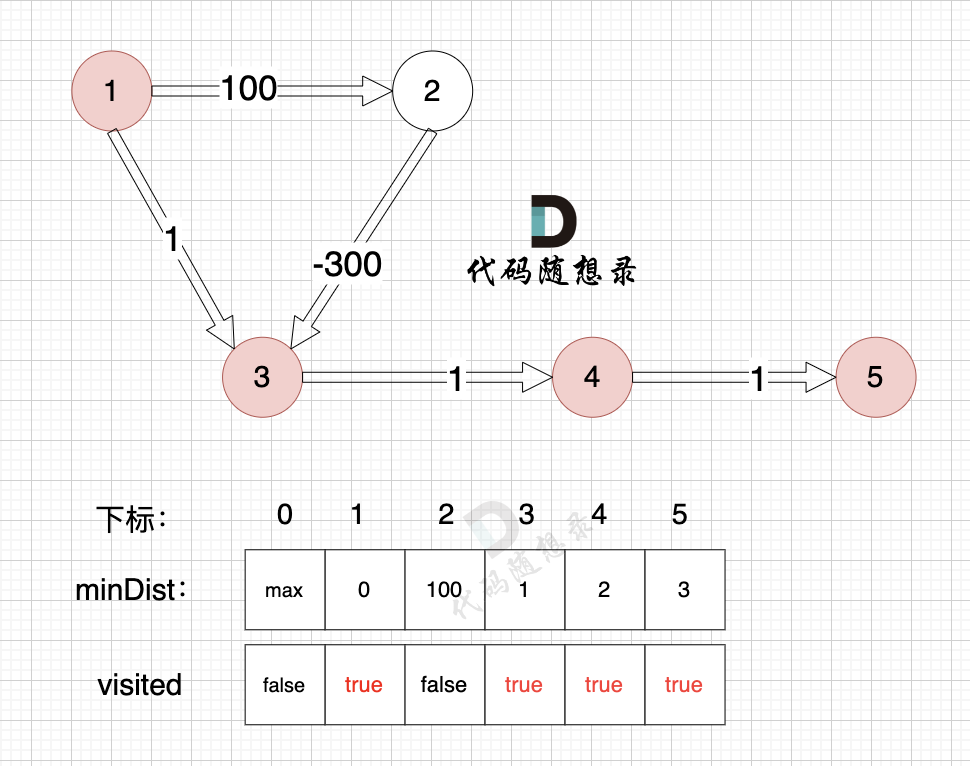
节点5的加入，而节点5 没有链接其他节点，所以不用更新minDist数组，仅标记节点5被访问过了

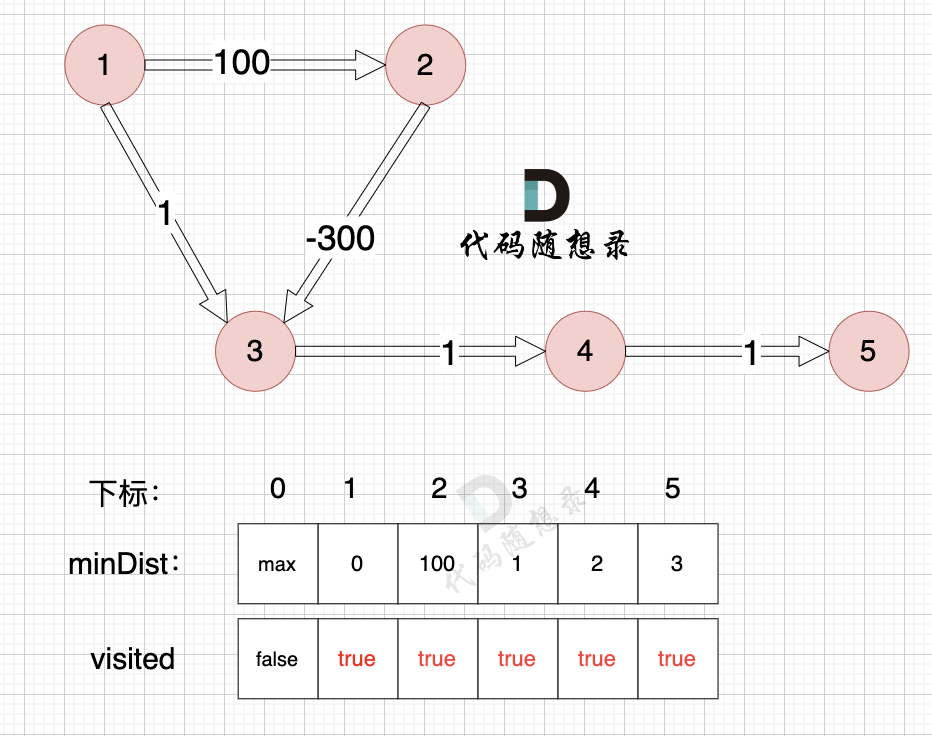
至此dijkstra的模拟过程就结束了，根据最后的minDist数组，我们求节点1 到节点5 的最短路径的权值总和为 3，路径：节点1 -> 节点3 -> 节点4 -> 节点5。通过以上的过程模拟，我们可以发现之所以没有走有负权值的最短路径是因为在访问节点 2 的时候，节点 3 已经访问过了，就不会再更新了。如果考虑改代码的话，访问过的节点还能继续访问会不会有死循环的出现呢？控制逻辑不让其死循环？那特殊情况？之类很多的问题出现。

对于负权值的出现，可以针对某一个场景不断去修改 dijkstra 的代码，但最终会发现只是拆了东墙补西墙，对dijkstra的补充逻辑只能满足某特定场景最短路求解。

关于dijkstra与prim算法的区别？

其实代码大体不差，唯一区别在三部曲中的第三步：更新minDist数组。因为prim是求非访问节点到最小生成树的最小距离，而 dijkstra是求非访问节点到源点的最小距离。

prim： minDist表示节点到最小生成树的最小距离，所以新节点cur的加入，只需要使用 grid[cur][j] ，grid[cur][j] 就表示 cur 加入生成树后，生成树到节点j 的距离。

dijkstra：minDist表示节点到源点的最小距离，所以新节点 cur 的加入，需要使用源点到cur的距离（minDist[cur]） + cur 到节点 v 的距离（grid[cur][v]），才是源点到节点v的距离。

prim算法可以有负权值，因为prim算法只需要将节点以最小权值和链接在一起，不涉及到单一路径。

import java.util.Arrays;
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(); // 节点数int m = scanner.nextInt(); // 边数// 邻接矩阵：grid[i][j] 表示从 i 到 j 的边权（Integer.MAX_VALUE 表示无边）int[][] grid = new int[n + 1][n + 1];for (int i = 0; i <= n; i++) {Arrays.fill(grid[i], Integer.MAX_VALUE);}// 读入 m 条有向边for (int i = 0; i < m; i++) {int u = scanner.nextInt();int v = scanner.nextInt();int w = scanner.nextInt();grid[u][v] = w; // 设置边权}int start = 1; // 起点int end = n;   // 终点// dist[i]：起点到节点 i 的最短距离int[] dist = new int[n + 1];Arrays.fill(dist, Integer.MAX_VALUE);dist[start] = 0;boolean[] visited = new boolean[n + 1]; // 标记是否已确定最短路径// Dijkstra 主循环：处理每个节点for (int i = 1; i <= n; i++) {// 找出未访问节点中距离起点最近的一个int cur = -1;int minDist = Integer.MAX_VALUE;for (int v = 1; v <= n; v++) {if (!visited[v] && dist[v] < minDist) {minDist = dist[v];cur = v;}}// 如果找不到，说明剩余节点不可达if (cur == -1) break;visited[cur] = true; // 标记为已访问// 用当前节点更新其邻居的距离for (int v = 1; v <= n; v++) {// 如果存在边 cur -> v，且通过 cur 能更短地到达 vif (!visited[v] && grid[cur][v] != Integer.MAX_VALUE) {if (dist[cur] + grid[cur][v] < dist[v]) {dist[v] = dist[cur] + grid[cur][v];}}}}// 输出结果if (dist[end] == Integer.MAX_VALUE) {System.out.println(-1); // 终点不可达} else {System.out.println(dist[end]); // 起点到终点的最短距离}scanner.close(); }
}

查看全文

http://www.dtcms.com/a/343109.html