什么是测度?
参考:https://zh.wikipedia.org/wiki/%E6%B5%8B%E5%BA%A6
1. 什么是测度
测度是一种数学工具,用来描述集合的“大小”。你可能已经熟悉一些简单的“大小”概念,比如长度、面积和体积。这些都可以看作是测度的具体例子。
- 长度:一条线段的长度是10厘米,这就是一个测度。
- 面积:一个正方形的面积是25平方厘米,这也是一个测度。
- 体积:一个立方体的体积是1000立方厘米,这还是一个测度。
但测度不仅仅局限于这些简单的几何形状,它可以推广到更复杂的集合上。比如,你可以用测度来描述一个不规则形状的面积,或者一个复杂集合的“大小”。
2. 测度的定义
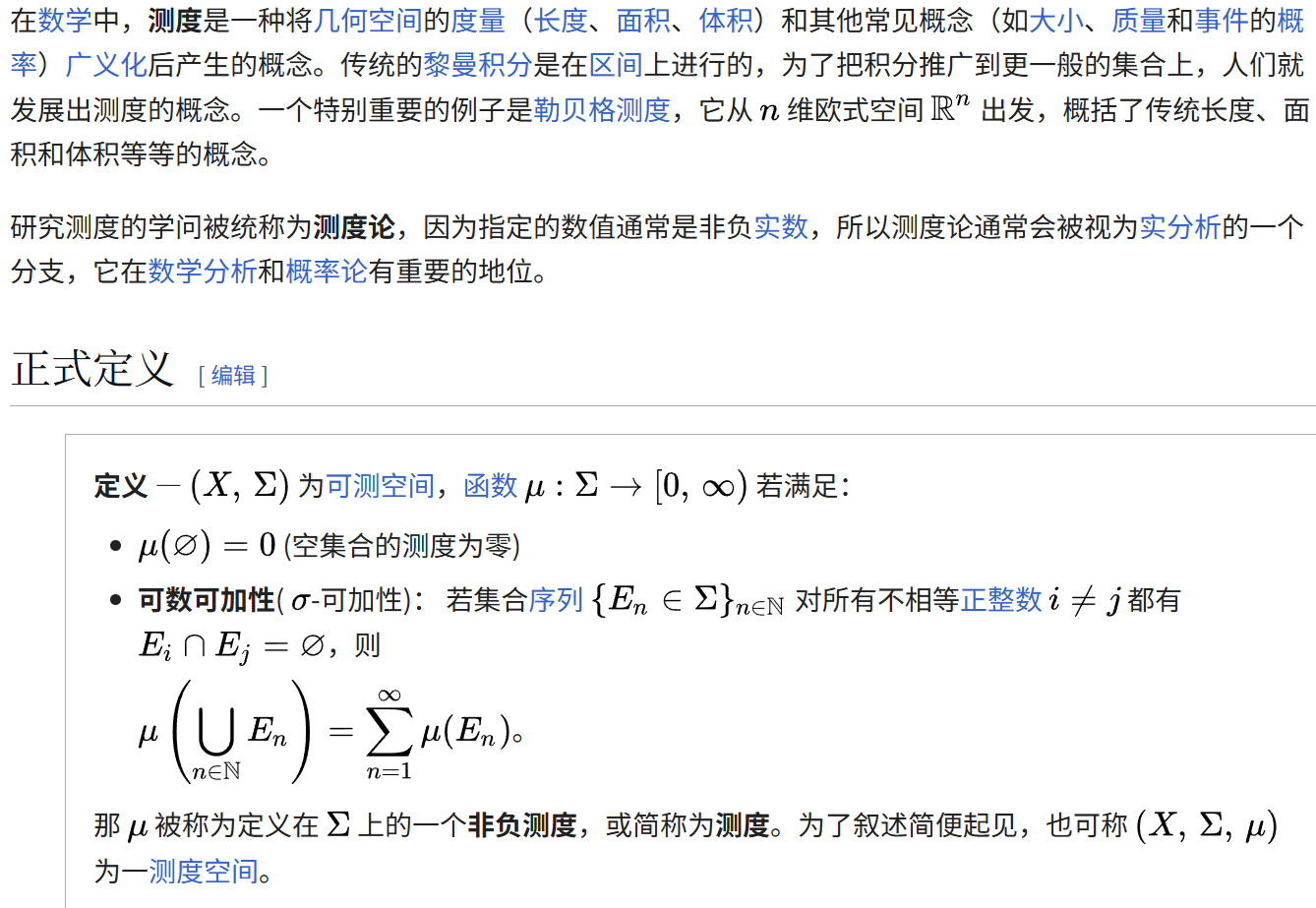
在数学中,测度是通过一些严格的规则来定义的。这些规则确保测度能够合理地描述集合的大小。具体来说,测度需要满足以下两个基本条件:
- 空集的测度为0:空集(什么都没有)的测度是0。这很直观,因为“什么都没有”的大小当然是0。
- 可数可加性:如果你有一些互不相交的集合(比如几个不重叠的区域),那么这些集合的并集的测度等于每个集合测度的和。比如,如果你有两个不相交的区域,一个面积是5,另一个面积是3,那么它们合并后的面积就是8。
3. 测度拿来干什么用
测度的一个重要用途是定义积分。你可能在高中学过简单的积分,比如计算一个函数在某个区间上的面积。但那种积分只适用于比较简单的函数和区间。测度的出现,让积分可以扩展到更复杂的情况。
- 勒贝格积分:这是测度理论中的一个重要概念。它比传统的黎曼积分更强大,可以处理更复杂的函数和集合。比如,你可以用勒贝格积分来计算一个函数在不规则区域上的积分,而这是传统的黎曼积分很难做到的。
4. 测度在整个数学体系中的地位
测度论是现代数学的一个重要分支,它在数学的很多领域都有重要的应用。
- 数学分析:测度论是数学分析的基础之一。它帮助我们更好地理解函数的性质,比如连续性、可积性等。通过测度论,我们可以定义更广泛的积分和导数,从而解决更复杂的数学问题。
- 概率论:概率论是测度论的一个重要应用领域。在概率论中,概率本身可以看作是一种测度。比如,一个事件发生的概率可以看作是这个事件在样本空间中的“大小”。通过测度论,我们可以更严格地定义概率,从而更准确地描述随机事件。
5. 测度对后续内容的重要性
如果你不是数学系的学生,测度论可能不会直接出现在你的课程中,但它在很多领域都有间接的影响。
- 统计学:统计学是概率论的应用,而概率论又是基于测度论的。所以,测度论为统计学提供了一个坚实的数学基础。
- 物理学:在物理学中,很多问题需要用到积分和概率。比如,计算一个物体的质量分布,或者描述一个粒子的行为。测度论为这些计算提供了更强大的工具。
- 工程学:在工程学中,信号处理、控制系统等领域也会用到测度论的思想。比如,描述信号的强度分布,或者系统的稳定性。
